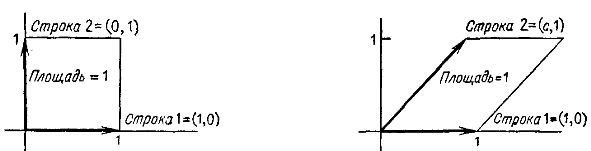Нахождение обратной матрицы: три алгоритма и примеры

Объем параллелепипеда

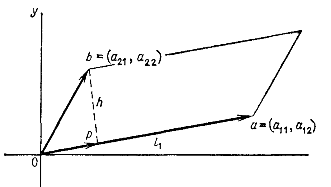
Связь между определителем и объемом не очевидна, однако мы можем предположить для начала, что все углы прямые, т. е. грани взаимно перпендикулярны, и мы имеем дело с прямоугольным параллелепипедом. Тогда объем его равен просто произведению длин ребер .

Мы хотим получить ту же самую формулу с помощью определителя. С этой целью вспомним, что ребра параллелепипеда представляются строками матрицы . В нашем случае эти строки
взаимно ортогональны, так что

Величины суть квадраты длин строк матрицы, т. е. квадраты длин ребер, и нули вне диагонали получаются вследствие ортогональности строк. Переходя к определителям, получаем

Извлекая корень, мы и приходим к требуемому соотношению:
определитель равняется объему. Знак при будет зависеть от того, образуют ребра правостороннюю систему координат вида или левостороннюю .

Если область не прямоугольна, то объем уже не равен произведению длин ребер. В плоском случае «объем» параллелограмма равен произведению длины основания на высоту .

Вектор длины есть разность между вектором второй строки и его проекцией на вектор первой строки.

Площадь паралелограмма равна .

Площади квадрата и параллелограмма.

Первый представляет собой единичный квадрат, и его площадь, равна 1. Второй есть параллелограмм с единичными основанием и высотой; его площадь не зависит от «сдвига», даваемого коэффициентом , и равна 1.

Минор $M_{ij}$ элемента $a_{ij}$

$M_{ij}$ элемента
$a_{ij}$ матрицы $A_{n\times n}$ именуют определитель матрицы, полученной из матрицы $A$ вычёркиванием i-й строки и j-го столбца (т.е. строки и столбца, на пересечении которых находится элемент $a_{ij}$).

Для примера рассмотрим квадратную матрицу четвёртого порядка:
$A=\left(\begin{array} {ccc}
1 & 0 & -3 & 9\\
2 & -7 & 11 & 5 \\
-9 & 4 & 25 & 84\\
3 & 12 & -5 & 58 \end{array} \right)$. Найдём минор элемента $a_{32}$, т.е. найдём $M_{32}$. Сперва запишем минор $M_{32}$, а потом вычислим его значение. Для того, чтобы составить $M_{32}$, вычеркнем из матрицы $A$ третью строку и второй столбец (именно на пересечении третьей строки и второго столбца расположен элемент $a_{32}$). Мы получим новую матрицу, определитель которой и есть искомый минор $M_{32}$:

Этот минор несложно вычислить, используя формулу №2 из темы вычисления :

$$
M_{32}=\left| \begin{array} {ccc}
1 & -3 & 9\\
2 & 11 & 5 \\
3 & -5 & 58 \end{array} \right|=
1\cdot 11\cdot 58+(-3)\cdot 5\cdot 3+2\cdot (-5)\cdot 9-9\cdot 11\cdot 3-(-3)\cdot 2\cdot 58-5\cdot (-5)\cdot 1=579.
$$

Итак, минор элемента $a_{32}$ равен 579, т.е. $M_{32}=579$.

Часто вместо словосочетания «минор элемента матрицы» в литературе встречается «минор элемента определителя». Суть остается неизменной: чтобы получить минор элемента $a_{ij}$ нужно вычеркнуть из исходного определителя i-ю строку и j-й столбец. Оставшиеся элементы записывают в новый определитель, который и является минором элемента $a_{ij}$. Например, найдём минор элемента $a_{12}$ определителя
$\left| \begin{array} {ccc}
-1 & 3 & 2\\
9 & 0 & -5 \\
4 & -3 & 7 \end{array} \right|$. Чтобы записать требуемый минор $M_{12}$ нам понадобится вычеркнуть из заданного определителя первую строку и второй столбец:

Чтобы найти значение данного минора используем формулу №1 из темы вычисления определителей второго и третьего порядков :

$$
M_{12}=\left| \begin{array} {ccc}
9 & -5\\
4 & 7 \end{array} \right|=9\cdot 7-(-5)\cdot 4=83.
$$

Итак, минор элемента $a_{12}$ равен 83, т.е. $M_{12}=83$.

Минор k-го порядка матрицы $A_$

Если в предыдущих двух пунктах мы говорили лишь о квадратных матрицах, то здесь поведём речь также и о прямоугольных матрицах, у которых количество строк вовсе не обязательно равняется количеству столбцов. Итак, пусть задана матрица $A_$, т.е. матрица, содержащая m строк и n столбцов.

Например, рассмотрим такую матрицу:

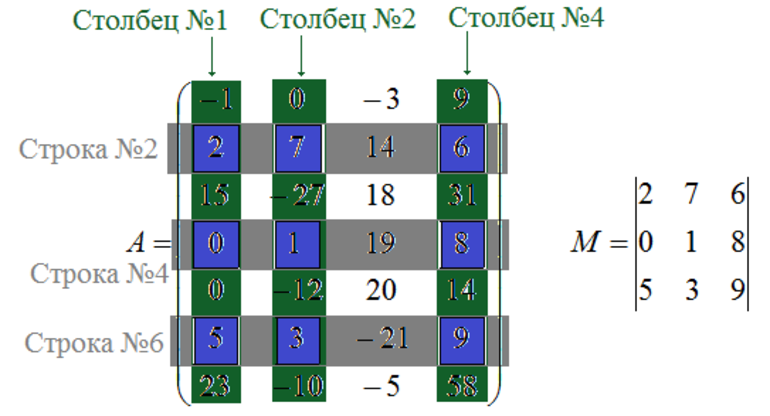
$$A=\left( \begin -1 & 0 & -3 & 9\\ 2 & 7 & 14 & 6 \\ 15 & -27 & 18 & 31\\ 0 & 1 & 19 & 8\\ 0 & -12 & 20 & 14\\ 5 & 3 & -21 & 9\\ 23 & -10 & -5 & 58 \end \right) $$

Запишем для неё какой-либо минор третьего порядка. Чтобы записать минор третьего порядка нам потребуется выбрать какие-либо три строки и три столбца данной матрицы. Например, возьмём строки №2, №4, №6 и столбцы №1, №2, №4. На пересечении этих строк и столбцов будут располагаться элементы требуемого минора. На рисунке элементы минора показаны синим цветом:

Миноры первого порядка находятся на пересечении одной строки и одного столбца, т.е. миноры первого порядка равны элементам заданной матрицы.

Напомню, что главными диагональными элементами именуют те элементы матрицы, у которых индексы равны: $a_$, $a_$, $a_$ и так далее. Например, для рассмотренной выше матрицы $A$ такими элементами будут $a_=-1$, $a_=7$, $a_=18$, $a_=8$. На рисунке они выделены зелёным цветом:

$$\left( \begin \boldgreen & 0 & -3 & 9\\ 2 & \boldgreen & 14 & 6 \\ 15 & -27 & \boldgreen & 31\\ 0 & 1 & 19 & \boldgreen\\ 0 & -12 & 20 & 14\\ 5 & 3 & -21 & 9\\ 23 & -10 & -5 & 58 \end \right) $$

Например, если в матрице $A$ мы вычеркнем строки и столбцы с номерами 1 и 3, то на их пересечении будут расположены элементы минора второго порядка, на главной диагонали которого будут находиться только диагональные элементы матрицы $A$ (элементы $a_=-1$ и $a_=18$ матрицы $A$). Следовательно, мы получим главный минор второго порядка:

$$ M=\left|\begin \boldgreen & -3 \\ 15 & \boldgreen \end \right| $$

Естественно, что мы могли взять иные строки и столбцы, – например, с номерами 2 и 4, получив при этом иной главный минор второго порядка.

Для примера рассмотрим такую матрицу:

$$A=\left( \begin -1 & 0 & 3 & 0 & 0 \\ 2 & 0 & 4 & 1 & 0\\ 1 & 0 & -2 & -1 & 0\\ 0 & 0 & 0 & 0 & 0 \end \right) $$

Запишем минор этой матрицы, элементы которого расположены на пересечении строк №1, №2, №3 и столбцов с №1, №3, №4. Мы получим минор третьего порядка (его элементы выделены в матрице $A$ фиолетовым цветом):

Найдём значение этого минора, используя формулу №2 из темы вычисления определителей второго и третьего порядков:

$$ M=\left| \begin -1 & 3 & 0\\ 2 & 4 & 1 \\ 1 & -2 & -1 \end \right|=4+3+6-2=11. $$

Итак, $M=11\neq 0$. Теперь попробуем составить любой минор, порядок которого выше трёх. Чтобы составить минор четвёртого порядка, нам придётся использовать четвёртую строку, однако все элементы этой строки равны нулю. Следовательно, в любом миноре четвёртого порядка будет нулевая строка, а это означает, что все миноры четвёртого порядка равны нулю. Миноры пятого и более высоких порядков составить мы не можем, так как матрица $A$ имеет всего 4 строки.

Мы нашли минор третьего порядка, не равный нулю. При этом все миноры высших порядков равны нулю, следовательно, рассмотренный нами минор – базисный. Строки матрицы $A$, на которых расположены элементы этого минора (первая, вторая и третья), – базисные строки, а первый, третий и четвёртый столбцы матрицы $A$ – базисные столбцы.

Данный пример, конечно, тривиальный, так как его цель – наглядно показать суть базисного минора. Вообще, базисных миноров может быть несколько, и обычно процесс поиска такого минора куда сложнее и объёмнее.

Введём ещё одно понятие – окаймляющий минор.

Для примера обратимся к такой матрице:

$$A=\left( \begin -1 & 2 & 0 & -2 & -14\\ 3 & -17 & -3 & 19 & 29\\ 5 & -6 & 8 & -9 & 41\\ -5 & 11 & 19 & -20 & -98\\ 6 & 12 & 20 & 21 & 54\\ -7 & 10 & 14 & -36 & 79 \end \right) $$

Запишем минор второго порядка, элементы которого расположены на пересечении строк №2 и №5, а также столбцов №2 и №4. Эти элементы выделены в матрице красным цветом:

Добавим к набору строк, на которых лежат элементы минора $M$, ещё строку №1, а к набору столбцов – столбец №5. Получим новый минор $M’$ (уже третьего порядка), элементы которого расположены на пересечении строк №1, №2, №5 и столбцов №2, №4, №5. Элементы минора $M$ на рисунке выделены красным цветом, а элементы, которые мы добавляем к минору $M$ – синим:

Минор $M’$ является окаймляющим минором для минора $M$. Аналогично, добавляя к набору строк, на которых лежат элементы минора $M$, строку №4, а к набору столбцов – столбец №3, получим минор $M»$ (минор третьего порядка):

Минор $M»$ также является окаймляющим минором для минора $M$.

Системы линейных алгебраических уравнений. Матричная запись системы. Основные определения

Системой линейных уравнений с неизвестными называется система вида

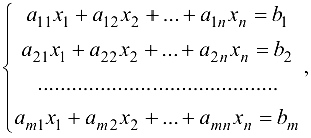(1.11)

где — действительные числа, называемые коэффициентами системы

— неизвестные системы; — свободные члены системы.

Все неизвестные в первой степени, поэтому система (1.11)- это система линейных уравнений. Если все свободные члены системы (1.11) равны нулю, то система называется однородной.

Матрица составленная из коэффициентов системы, называется матрицей системы. Матрица полученная из матрицы добавлением столбца свободных членов, называется расширенной матрицей системы

Если через обозначить матрицу-столбец из неизвестных, т. е.

а через — матрицу-столбец свободных членов, т. е. то так как матрица (имеет столбцов) согласована с матрицей (имеет строк), произведение существует и линейную систему (1.11) можно записать в матричном виде

Упорядоченная совокупность чисел называется решением системы (1.11), если каждое из уравнений (1.11) обращается в верное равенство после подстановки вместо соответственно чисел

Решение системы, записанное в виде матрицы-столбца

называется вектор-решением системы.

Если существует хотя бы одно решение системы (1.11), то она называется совместной, и несовместной, если она не имеет решений.

Совместная система называется определенной, если она имеет единственное решение.

Система, имеющая более одного решения, называется неопределенной.

Решить систему — это значит выяснить, совместна она или несовместна, и в случае совместности найти все ее решения.

Две системы называются эквивалентными или равносильными, если всякое решение одной из них является решением другой и наоборот.

Габриель Крамер (1704-1752) — швейцарский математик, один из создателей линейной алгебры. Рассмотрим систему линейных уравнений с неизвестными.

(1.12)

или

(1.12′)

Определитель матрицы А имеет вид

и называется определителем системы. Если то система называется невырожденной. Найдем решение системы, предполагая что В этом случае матрица невырожденная и для нее существует единственная обратная матрица (по теоремам пп. 1.1.6)

Умножим матричное уравнение (1.12′) слева на и получим

(1.13)

Формула (1.13)- решение системы (1.12) в матричном виде. Это равенство можно записать так:

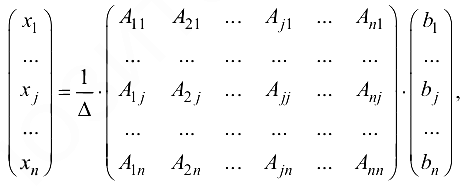
где или

(1.13′)

Из формулы (1.13′) видно, что любая переменная определяется по формуле

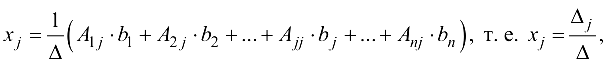(1.14)

где — определитель, полученный из заменой столбца столбцом свободных членов. Формулы (1.14) называются формулами Крамера.

Пример №1.10.

Решить систему

Решение:

Матрица имеет вид

Вычислим

Следовательно, матрица вырождена и система несовместна, т. е. нет решений.

Пример №1.11.

Решить систему

Решение:

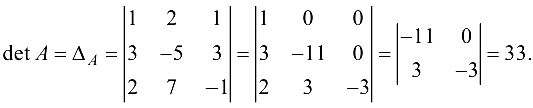
а) Так как то матрица невырожденная и решение системы найдем матричным методом, т. е. по формуле (1.13): Найдем обратную матрицу Составим алгебраические дополнения:

В данном случае матричное равенство (1.13) запишем в виде

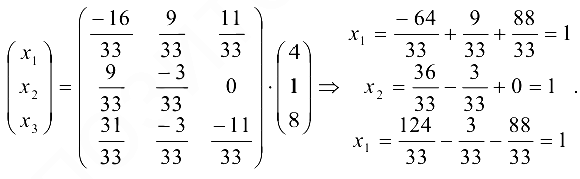
б) Решим данную систему по формулам Крамера (1.14):

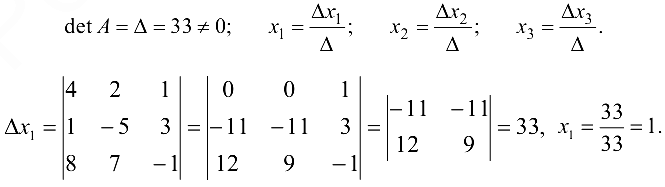
Ответ:

Определение определителя матрицы, вычисление определителя матрицы по определению.

Напомним несколько вспомогательных понятий.

Определение.

Перестановкой порядка n называется упорядоченный набор чисел, состоящий из n элементов.

Для множества, содержащего n элементов, существует n! (n факториал) перестановок порядка n. Перестановки отличаются друг от друга лишь порядком следования элементов.

Например, рассмотрим множество, состоящее из трех чисел: . Запишем все перестановки (всего их шесть, так как ):

Определение.

Инверсией в перестановке порядка n называется всякая пара индексов p и q, для которой p-ый элемент перестановки больше q-ого.

В предыдущем примере инверсией перестановки 4, 9, 7 является пара p=2, q=3, так как второй элемент перестановки равен 9 и он больше третьего, равного 7. Инверсией перестановки 9, 7, 4 будут три пары: p=1, q=2 (9>7); p=1, q=3 (9>4) и p=2, q=3 (7>4).

Нас будет больше интересовать количество инверсий в перестановке, а не сама инверсия.

Пусть — квадратная матрица порядка n на n над полем действительных (или комплексных) чисел. Пусть – множество всех перестановок порядка n множества . Множество содержит n! перестановок. Обозначим k–ую перестановку множества как , а количество инверсий в k-ой перестановке как .

Определение.

Определитель матрицы А есть число, равное .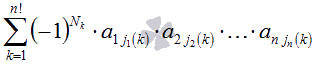

Опишем эту формулу словами. Определителем квадратной матрицы порядка n на n является сумма, содержащая n! слагаемых. Каждое слагаемое представляет собой произведение n элементов матрицы, причем в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы А. Перед k-ым слагаемым появляется коэффициент (-1), если элементы матрицы А в произведении упорядочены по номеру строки, а количество инверсий в k-ой перестановке множества номеров столбцов нечетно.

Определитель матрицы А обычно обозначается как , также встречается обозначение det(A). Также можно услышать, что определитель называют детерминантом.

Итак, .

Отсюда видно, что определителем матрицы первого порядка является элемент этой матрицы .

Вычисление определителя квадратной матрицы второго порядка — формула и пример.

Найдем определитель квадратной матрицы порядка 2 на 2 в общем виде.

В этом случае n=2, следовательно, n!=2!=2.

Оформим в виде таблицы необходимые данные для применения формулы .

Имеем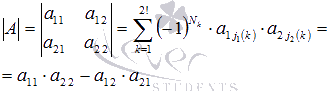

Таким образом, мы получили формулу для вычисления определителя матрицы порядка 2 на 2, она имеет вид .

Пример.

Вычислите определитель квадратной матрицы порядка .

Решение.

В нашем примере . Применяем полученную формулу :

Вычисление определителя квадратной матрицы третьего порядка — формула и пример.

Найдем определитель квадратной матрицы порядка 3 на 3 в общем виде.

В этом случае n=3, следовательно, n!=3!=6.

Оформим в виде таблицы необходимые данные для применения формулы .

Имеем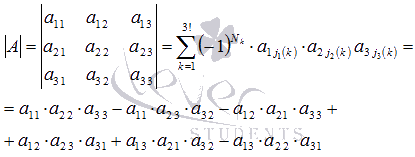

Таким образом, мы получили формулу для вычисления определителя матрицы порядка 3 на 3, она имеет вид

Аналогично можно получить формулы для вычисления определителей матриц порядка 4 на 4, 5 на 5 и более высоких. Они будут иметь очень громоздкий вид.

Пример.

Вычислите определитель квадратной матрицы порядка 3 на 3.

Решение.

В нашем примере

Применяем полученную формулу для вычисления определителя матрицы третьего порядка:

Формулы для вычисления определителей квадратных матриц второго и третьего порядков очень часто применяются, так что рекомендуем их запомнить.

4.Определители. Свойства определителей.

Квадратной матрице А порядка n можно сопоставить число det А (или |A|, или ), называемое ее определителем, следующим образом:

Определитель матрицы A также называют ее детерминантом. Правило вычисления детерминанта для матрицы порядка N является довольно сложным для восприятия и применения. Однако известны методы, позволяющие реализовать вычисление определителей высоких порядков на основе определителей низших порядков. Один из методов основан на свойстве разложения определителя по элементам некоторого ряда (свойство 7). При этом заметим, что определители невысоких порядков (1, 2, 3) желательно уметь вычислять согласно определению.

Вычисление определителя 2-го порядка иллюстрируется схемой:

Пример 4.1. Найти определители матриц

Решение:

При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса), которое символически можно записать так:

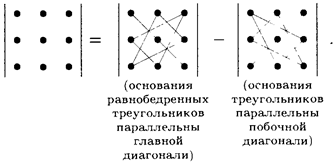
Пример 4.2. Вычислить определитель матрицы

Решение:

det А = 5*1*(-3) + (-2)*(-4)*6 + 3*0*1 — 6*1*1 — 3*(-2)*(-3) — 0*(-4)*5 = -15+48-6-18 = 48-39 = 9.

Сформулируем основные свойства определителей, присущие определителям всех порядков. Некоторые из этих свойств поясним на определителях 3-го порядка.

Свойство 1 («Равноправность строк и столбцов»). Определитель не изменится, если его строки заменить столбцами, и наоборот. Иными словами,

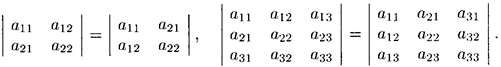
В дальнейшем строки и столбцы будем просто называть рядами определителя.

Свойство 2. При перестановке двух параллельных рядов определитель меняет знак.

Свойство 3. Определитель, имеющий два одинаковых ряда, равен нулю.

Свойство 4. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.

Действительно,

Свойство 5. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

Например,

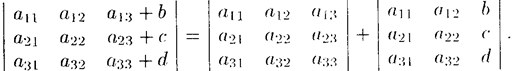
Свойство 6. («Элементарные преобразования определителя»). Определитель не изменится, если к элементам одною ряда прибавить соответствующие элементы параллельного ряда, умноженные па любое число.

Пример 4.3. Доказать, что

Решение: Действительно, используя свойства 5, 4 и 3 подучим

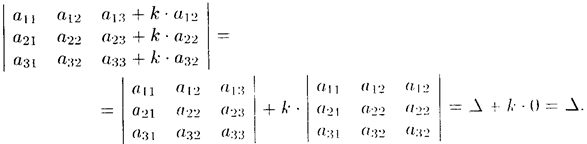
Дальнейшие свойства определителей связаны с понятиями минора и алгебраического дополнения.

Минором некоторого элемента аij определителя n-го порядка называется определитель n — 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, па пересечении которых находится выбранный элемент. Обозначается mij

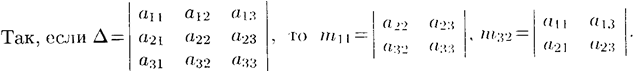
Алгебраическим дополнением элемента aij определителя называется его минор, взятый со знаком «плюс», если сумма i + j четное число, и со знаком «минус», если эта сумма нечетная. Обозначается Aij :

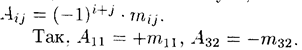
Свойство 7 («Разложение определителя по элементам некоторого ряда»). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.

Проиллюстрируем и одновременно докажем свойство 7 на примере определителя 3-его порядка. В этом случае свойство 7 означает, что

В самом деле, имеем

Свойство 7 содержит в себе способ вычисления определителей высоких порядков.

Пример 4.4. Вычислите определитель матрицы

Решение: Для разложения определителя обычно выбирают гот ряд, где есть нулевые элементы, т. к. соответствующие им слагаемые в разложении будут равны нулю.

Свойство 8. Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
Так, например,

Posted in Высшая математика, Лекции 1 курс and tagged Высшая математика

Расчёт определителя

В линейной алгебре существует понятие определителя или детерминанта. Это число, которое ставят в соответствие каждой квадратной матрице, вычисленное из её элементов по специальной формуле. Определитель или модуль используется для решения большинства задач. Детерминант самой простой матрицы определяется с помощью вычитания перемноженных элементов из побочной диагонали и главной.

Произведения могут отличаться друг от друга составом элементов. Со знаком плюс будут включаться в сумму числа, если их индексы составляют чётную подстановку, в противоположном случае их значение меняется на минус. Определитель обозначается символом det A. Круглые скобки матричной таблицы, обрамляющие её элементы, заменяются на квадратные. Формула определителя:

Определитель первого порядка, состоящий из одного элемента, равен самому этому элементу. Детерминант матричной таблицы размером 2*2 второго порядка вычисляется путём перемножения её элементов, расположенных на главной диагонали, и вычитания из них произведения элементов, находящихся в побочной диагонали. Наглядный пример:

Для матрицы также можно найти дискриминант многочлена, отвечающий формуле:

Когда у многочлена имеются кратные корни, тогда дискриминант равен нулю.

Нахождение обратной матрицы методом алгебраических дополнений (союзной матрицы)

Для неособенной квадратной матрицы А обратной является матрица

,  (2)

где —
определитель матрицы А, а

— матрица, союзная с матрицей А.

Разберём ключевые понятия, которые потребуются для решения задач — союзная матрица, алгебраические дополнения и транспонированная матрица.

Пусть существует квадратная матрица A:

Транспонированная относительно матрицы A матрица A’ получается,
если из строк матрицы A сделать столбцы, а из её столбцов — наоборот, строки, то есть заменить строки
столбцами:

Остановимся на минорах и алгебраических дополнениях.

Пусть есть квадратная матрица третьего порядка:

.

Её определитель:

Вычислим алгебраическое дополнение элемента ,
то есть элемента 2, стоящего на пересечении первой строки и второго столбца.

Для этого нужно сначала найти минор этого элемента. Он получается вычёркиванием из
определителя строки и столбца, на пересечении которых стоит указанный элемент. В результате останется
следующий определитель, который и является минором элемента :

.

Алгебраическое дополнение элемента
получим, если умножим ,
где i — номер строки исходного элемента, а k — номер столбца исходного элемента, на
полученный в предыдущем действии минор этого исходного элемента. Получаем алгебраическое дополнение элемента
:

.

По этой инструкции нужно вычислить алгебраические дополнения всех элементов матрицы
A’, транспонированной относительно матрицы матрица A.

И последнее из значимых для нахождение обратной матрицы понятий. Союзной с квадратной матрицей A называется матрица

того же порядка, элементами которой являются алгебраические дополнения соответствующих элементов определителя матрицы
,
транспонированной относительно матрицы A. Таким образом, союзная матрица состоит из следующих элементов:

Алгоритм нахождения обратной матрицы методом алгебраических дополнений

1. Найти определитель данной матрицы A. Если определитель равен нулю, нахождение
обратной матрицы прекращается, так как матрица вырожденная и обратная для неё не существует.

2. Найти матрицу, транспонированную относительно A.

3. Вычислить элементы союзной матрицы как алгебраические дополнения марицы, найденной на шаге 2.

4. Применить формулу (2): умножить число, обратное определителю матрицы A,
на союзную матрицу, найденную на шаге 4.

5. Проверить полученный на шаге 4 результат, умножив данную матрицу A на
обратную матрицу. Если произведение этих матриц равно единичной матрицы, значит обратная матрица была
найдена верно. В противном случае начать процесс решения снова.

Пример 1. Для матрицы

найти обратную матрицу.

Решение. Для нахождения обратной матрицы необходимо найти определитель матрицы А .
Находим по правилу треугольников:

Следовательно, матрица А – неособенная (невырожденная, несингулярная) и для неё существует обратная.

Найдём матрицу, союзную с данной матрицей А.

Найдём матрицу
,
транспонированную относительно матрицы A:

Вычисляем элементы союзной матрицы как алгебраические дополнения матрицы,
транспонированной относительно матрицы A:

Следовательно, матрица
,
союзная с матрицей A, имеет вид

Замечание. Порядок вычисления элементов и транспонирования матрицы может
быть иным. Можно сначала вычислить алгебраические дополнения матрицы A, а затем транспонировать
матрицу алгебраических дополнений. В результате должны получиться те же элементы союзной матрицы.

Применяя формулу (2), находим матрицу, обратную матрице А:

Проверить решение можно с помощью онлайн калькулятора
для нахождения обратной матрицы.

Использование интернет-калькулятора

В интернете есть определённая группа сайтов, позволяющая выполнять различные математические вычисления в автоматическом режиме. На их страницах содержится специальный скрипт, выполняющий нахождение минора матрицы онлайн любой сложности. При этом от потребителя не требуется никаких особых знаний, он даже и вовсе может ничего не понимать в алгебраических вычислениях.

Всё, что ему необходимо будет сделать для получения ответа, — это ввести исходные данные в предложенную форму и нажать кнопку «Вычислить». Система автоматически определит нужный алгоритм и, используя свойства матрицы, выведет на экран ответ. При этом, кроме результата, пользователю будет предоставлена возможность ознакомиться с подробным решением.

По отзывам потребителей, из множества таких сервисов можно выделить пять следующих сайтов:

1. Allcalc — сервис с простым интерфейсом, но в то же время позволяющий выполнить любые действия с матрицей, включая нахождение миноров и алгебраических дополнений.
2. Onlinemschool — сайт, умеющий не только быстро выполнять вычисления, но и выводить пошаговое решение с комментариями.
3. MathSemestr — программное обеспечение калькулятора, понимает даже соотношения, взятые из таких популярных программ, как World и Excel.
4. Pikod — бесплатный сайт, предлагающий получить не только ответ, но и подробно расписанный ход решения.
5. Kontrolnaya-rabota — сервис позволяет выполнять любые преобразования матриц, при этом для сложных заданий существует режим «модульный конструктор».

Все указанные сайты доступны на русском языке, бесплатны, имеют простой и понятный интерфейс. На их страницах содержится справочная и теоретическая математическая информация. Кроме неё, для каждого раздела приводится типовой пример с объяснением. Использование онлайн-калькуляторов поможет сэкономить время и научит правильно выполнять действия по вычислению миноров.

Их использование будет полезным не только ученикам или студентам, желающим научиться самостоятельно решать задачи, но и инженерам, выполняющим сложные вычисления. Для специалистов они довольно востребованы, так как при самостоятельном решении небольшая ошибка по невнимательности приведёт к неправильному ответу, что исключено при расчёте в автоматическом режиме.