Как найти определитель матрицы: второго, третьего, произвольного порядка

Свойства определителя матриц

1. Строки и столбцы определителя одинаковы, то есть значение определителя не изменится, если вы поменяете местами строки и столбцы, сохранив их порядок. Это называется переносом квалификатора. В соответствии с сформулированным свойством det A = det AT.
2. При обмене двумя строками (или двумя столбцами) определитель сохраняет свое абсолютное значение, но меняет знак на противоположный.
3. Определитель с двумя идентичными строками (или столбцами) равен нулю.
4. Умножение всех элементов строки (или столбца) определителя на число эквивалентно умножению определителя на число λ.
5. Если все элементы любой строки (или столбца) определителя равны нулю, то сам определитель равен нулю.
6. Если элементы определителя с двумя строками (или двумя столбцами) пропорциональны, то определитель равен нулю.
7. Если к элементам некоторой строки (или некоторого столбца) определителя добавить соответствующие элементы другой строки (другого столбца), умноженные на произвольный коэффициент λ, то значение определителя не изменится.
8. Сумма произведений элементов любой строки (любого столбца) определителя на соответствующие алгебраические дополнения элементов любой другой строки (любого другого столбца) равна нулю.
9. Если все элементы i-й строки определителя представить в виде суммы двух слагаемых aij = bj + cj, то определитель равен сумме двух определителей, в которой все строки, кроме i-й, совпадают с заданным определителем, i-я строка в одном из слагаемых состоит из элементов bj, а в другом — из элементов cj. Аналогичное свойство верно и для определения столбцов.
10. Определитель произведения двух квадратных матриц равен произведению их определителей: det (A * B) = det A * det B.

Для вычисления определителя любого порядка можно использовать метод последовательных уменьшений порядка определителя.

Для этого используйте детерминантное правило декомпозиции для элементов строки или столбца. Другой способ вычисления определителей состоит в использовании элементарных преобразований со строками (или столбцами), в основном в соответствии со свойствами 4 и 7 определителей, для приведения определителя к форме, когда он находится под главной диагональю определителя (определенным в то же время).

Кстати, как и для квадратных матриц) все элементы равны нулю. Тогда определитель равен произведению элементов, расположенных на главной диагонали.

При вычислении определителя путем последующего уменьшения порядка для уменьшения объема вычислительной работы рекомендуется использовать свойство определителя 7 для обнуления некоторых элементов любой строки или столбца определителя, что уменьшит количество алгебраических дополнений.

Часто задаваемые вопросы (FAQ):

Для чего используются детерминанты?

Определитель полезен при определении решения линейных уравнений, фиксируя, как линейное преобразование изменяет объем или площадь и изменяет переменные в интегралах. Он отображается как функция, вход которой представляет собой квадратную матрицу, а выход представляет собой одно число.

Что означает определитель 0?

Определитель 0 означает, что объем равен нулю (0). Это может произойти только тогда, когда один вектор перекрывает один другой.

Может ли определитель быть отрицательным?

Поскольку это действительное число, а не матрица. Значит, это может быть отрицательное число. Определитель существует только для квадратных матриц (2 × 2, 3 × 3, … n × n).

Свойства определителя матрицы

1. Определитель равен единице:

   det(E) = 1

2. Определитель матрицы с двумя равными строками (столбцами) равен нулю.
3. Определитель матрицы с двумя пропорциональными строками (столбцами) равен нулю.
4. Определитель матрицы, содержащий нулевую строку (столбец), равен нулю.
5. Определитель матрицы равен нулю если две (или несколько) строк (столбцев) матрицы линейно зависимы.
6. При транспонировании значение определителя матрицы не меняется:

   det(A) = det(AT)

7. Определитель обратной матрицы:

   det(A-1) = det(A)-1

8. Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить другую строку (столбец), умноженную на некоторое число.
9. Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить линейную комбинации других строк (столбцов).
10. Если поменять местами две строки (столбца) матрицы, то определитель матрицы поменяет знак.
11. Общий множитель в строке (столбце) можно выносить за знак определителя:
    

    11 12 … 1 21 22 … 2 . . . . ·1 ·2 … · . . . . 1 2 …

    =

    11 12 … 1 21 22 … 2 . . . . 1 2 … . . . . 1 2 …

12. Если квадратная матрица -того порядка умножается на некоторое ненулевое число, то определитель полученной матрицы равен произведению определителя исходной матрицы на это число в -той степени:

    B = ·A   =>   det(B) = ·det(A)

    где A матрица ×, — число.

13. Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем:
    

    11 12 … 1 21 22 … 2 . . . . 1 + 1 2 + 2 … + . . . . 1 2 …

    =

    11 12 … 1 21 22 … 2 . . . . 1 2 … . . . . 1 2 …

    +

    11 12 … 1 21 22 … 2 . . . . 1 2 … . . . . 1 2 …

14. Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
15. Определитель произведения матриц равен произведению определителей этих матриц:

    det(A·B) = det(A)·det(B)

Вычисление определителя матрицы при помощи метода Гаусса

Вспомним, как метод Гаусса помогает находить определитель матрицы: благодаря элементарным преобразованием в матрице все элементы (кроме ) нужно привести к нулю. Однако, такой метод подходит только к тем матрицам, в которых определитель отличен от нуля. Об этом поговорим позже, а сейчас объясним, для чего проделывается такая процедура.

Нулевые элементы необходимы для того, чтобы самым простым способом разложить определитель, исходя из элементов первого столбца. После такого преобразования, исходя из девятого свойства  и , получается:

.

Здесь – это минор первого порядка, который получился из матрицы путём вычёркивания элементов первой строки и первого столбца. Такая процедура проделывается до тех пор, пока все элементы первого столбца не превратятся в нулевые элементы.

Конечно же, сразу же назревает вопрос: “А как же получается нулевые элементы?” Рассмотрим алгоритм решения:

Если первый элемент в первой строке и в первом столбце прибавить к соответствующим элементом – ой строки, где . (Метод Гаусса не нужен только в том случае, если все элементы в первом столбцы нулевые). После данного преобразования “новый” элемент матрицы . Определитель “новой” матрицы равен определителю исходной матрицы.

Если , тогда к каждому элементу второй строки прибавляем элемент первой строки, которые заранее умноженные на , а к элементам третьей строки прибавляем определённые элементы первой строки, которые умножаются на . И дальше вычисляем по такой же схеме. Метод Гаусса рассмотрен более подробно в отдельно теме. В итоге получится преобразованная матрица, где все элементы первого столбца окажутся нулевыми. Определитель полученной матрицы будет равен определителю изначальной матрицы.

Напомним, что величина определителя – ого порядка равна сумме произведений элементов какой-либо строки или столбца на соответствующее алгебраическое дополнение.

Рассмотрим записанный сначала формально определитель четвёртого порядка:

Вычёркивая в – тую строку и – тый столбец, на пересечении которого помещается элемент , получим определитель третьего порядка, который называется минором элемента и обозначается . Тогда – алгебраическое дополнение элемента . Определитель 4-го порядка можно обозначить, как размещение по элементам, например, первого столбца:

Пусть введено понятие определителя – ого порядка, тогда определитель – ого порядка:

Можно изобразить, как размещение по элементам первого столбца:

,

где – алгебраические дополнения, а – миноры элементов первого столбца. Последние и есть определители – го порядка.

Чтобы было более понятно, разберём матрицу четвёртого порядка, где нужно найти определитель:

Разберём на примере:

Пример 4

Задача

Нужно вычислить определитель матрицы высшего порядка x :

Решение

Сначала вспомним тему про определители третьего порядка и превратим в нули элементы 1-го столбца, которые принадлежат 2, 3, 4 строкам. Для этого прибавим соответствующие элементы 1 и 2 строк. На месте элементов получим , , , .

Чтобы получить в 3 строке 1-го столбца, умножим на элементы 1-ой строки и прибавим к соответствующим элементам третьей строки:

Умножим элементы 1-ой строки на и добавим к соответствующим элементам 4-ой строки. Получается:

Изначальный определитель впоследствии преобразований получается:

Дальше раскладываем последний определитель за элементами 1-го столбца. Поскольку , а остальные элементы 1-го столбца нули, тогда получим один определитель  3-го порядка.

Ответ

Определитель матрицы четвёртого порядка = .

Определитель матрицы 3×3 — ChiliMath

Стандартная формула для нахождения определителя матрицы 3×3 представляет собой разбивку более мелких задач на определитель 2×2 , с которыми очень легко справиться.

Определитель матрицы A вычисляется как

Вот ключевые моменты:

Обратите внимание, что элементы верхней строки, а именно a, b и c, служат скалярными множителями для соответствующей матрицы 2 на 2. Скаляр a умножается на матрицу 2×2 оставшихся элементов, созданную при рисовании вертикальных и горизонтальных отрезков, проходящих через a

Скаляр a умножается на матрицу 2×2 оставшихся элементов, созданную при рисовании вертикальных и горизонтальных отрезков, проходящих через a.

Тот же процесс применяется для построения матриц 2×2 для скалярных множителей b и c.

Приведенные ниже практические задачи помогут вам проверить, знаете ли вы, как найти определитель матрицы 3×3. Не стесняйтесь использовать его в качестве дополнительного учебного материала.

Определитель матрицы 3×3 Практические задачи

Примеры поиска определителя матрицы 3×3

Пример 1: Найдите определитель матрицы 3×3 ниже.

Приведенная ниже установка поможет вам найти соответствие между общими элементами формулы и элементами реальной задачи.

Применение формулы

Пример 2: Оцените определитель матрицы 3×3 ниже.

Будьте очень осторожны при подстановке значений в нужные места в формуле. Распространенные ошибки возникают, когда учащиеся проявляют небрежность на начальном этапе подстановки значений.

Кроме того, не торопитесь, чтобы убедиться, что ваши арифметические расчеты также верны. В противном случае единственная ошибка где-то в расчетах приведет к неправильному ответу в конце.

Так как,

наш расчет определителя становится…

Пример 3: Найдите определитель матрицы 3×3 ниже.

Наличие нуля (0) в первой строке должно значительно упростить наши вычисления. Помните, что элементы в первой строке действуют как скалярные множители. Следовательно, ноль, умноженный на что-либо, приведет к исчезновению всего выражения.

Вот снова настройка, чтобы показать соответствующее числовое значение каждой переменной в формуле.

Используя формулу, мы имеем…

Пример 4: Найдите определитель матрицы 3×3 ниже.

\большой{\begin{bmatrix}
1 и -2 и 3 \\
2 и 0 и 3 \\
1 и 5 и 4
\end{bmatrix}}

Решение :

Пример 5 : Вычислите определитель матрицы три на три ниже.

\большой{\begin{bmatrix}
-5&-5&-5\
3&-1&-2\
4 и 2 и 1
\end{bmatrix}}

Решение :

Вас также может заинтересовать:

Определители матрицы 2×2

Вычисление определителя матрицы второго порядка

Чаще всего на практике определитель матрицы решается методами второго, третьего и реже, четвёртого порядка. Рассмотрим, как вычисляется определитель матрицы второго порядка:

В матрице второго порядка , отсюда следует, что факториал . Прежде чем применить формулу

необходимо определить, какие данные у нас получаются:

1. ;

2. перестановки множеств: и ;

3. количество инверсий в перестановке : и , так как ;

4. соответствующие произведения : и .

Получается:

Исходя из вышесказанного мы получаем формулу для вычисления определителя квадратной матрицы второго порядка, то есть x :

Рассмотрим на конкретном примере, как вычислять определитель квадратной матрицы второго порядка:

Пример

Задача

Вычислить определитель матрицы x :

Решение

Итак, у нас получается , , , .

Для решения необходимо воспользоваться ранее рассмотренной формулой:

Подставляем числа с примера и находим:

Ответ

Определитель матрицы второго порядка = .

Единственность детерминанта.

Начнем с того, что с помощью известных нам свойств детерминанта вычислим детерминанты элементарных матриц.

Если матрица S_{1} получена из единичной умножением какой-либо строки на число \lambda \neq 0, то \mathbf{det}\,S_{1}=\lambda \mathbf{det}\,E=\lambda, согласно свойству линейности детерминанта по строке. Если матрица S_{2} получена из единичной матрицы прибавлением одной строки к другой, то из видно, что \mathbf{det}\,S_{2}=\mathbf{det}\,E=1. Таким образом, имеет место

Утверждение 5.

Если существуют две функции d_{1} и d_{2} удовлетворяющие определению детерминанта, то для любой элементарной матрицы d_{1}(S)=d_{2}(S).

Кроме того, легко проверить, что для любой матрицы A и любой элементарной матрицы S выполнено равенство \tag{4}\mathbf{det}\,(SA)=\mathbf{det}\,S \mathbf{det}\,A.
Действительно, достаточно вспомнить, что SA получается из A тем же элементарным преобразованием, что и S из E. Отсюда для матриц первого типа \mathbf{det}\,(S_{1}A)=\lambda \mathbf{det}\,A. Поскольку \mathbf{det}\,S_{1}=\lambda, равенство справедливо. Точно так же, для матриц второго типа \mathbf{det}\,(S_{2}A)=\mathbf{det}\,A и \mathbf{det}\,S_{2}=1.

Теперь может быть доказана

Теорема 1.

На множестве квадратных матриц порядка n не может быть более одной функции, удовлетворяющей определению детерминанта.

Пусть существуют две такие функции d_{1} и d_{2}. Докажем, что d_{1}(A)=d_{2}(A) для любой квадратной матрицы A. Если A — вырожденная матрица, то по определению d_{1}(A)=d_{2}(A)=0. Рассмотрим невырожденную матрицу A. По уже  она может быть разложена в произведение элементарных матриц. Последовательно применяя формулу , мы получаем d_{1}(A)=d_{1}(S_{1}…S_{N})=d_{1}(S_{1})d_{1}(S_{2}…S_{N})=…=d_{1}(S_{1})…d_{1}(S_{N}). Аналогично, d_{2}(A)=d_{2}(S_{1})…d_{2}(S_{N}) Теперь из следует d_{1}(A)=d_{2}(A), как и требовалось.

Вместе с доказательством теоремы, мы получили важную формулу: если невырожденная матрица A разложена в произведение элементарных матриц, то \tag{5} \mathbf{det}\,A=\mathbf{det}\,S_{1}…\mathbf{det}\,S_{N}.

Отметим, что детерминант элементарной матрицы либо равен числу \lambda \neq 0, либо равен единице, то есть в любом случае отличен от нуля. Из равенства тогда следует

Утверждение 6.

Если матрица невырожденная, то ее детерминант отличен от нуля.

Следствие.

Для того чтобы матрица была вырожденной, необходимо и достаточно, чтобы ее детерминант был равен нулю.

Как можно найти определитель матрицы второго порядка?

В основном студенты и ученики получают от преподавателей задание вычислить определитель матрицы второго, третьего, иногда четвёртого порядка. В первом случае решение типовое и достаточно понятное. Детально это происходит следующим образом:

\

это квадратная матрица второго порядка, определителем которой называется число

\

Посчитать определитель подобной матрицы можно здесь так:

В матрице 2-го порядка n = 2, отсюда следует, что факториал n! = 2! = 2. До момента применения формулы

\

важно разобраться с данными, которые мы получаем:

1. k = 2;
2. перестановки множеств 1,2 и 2,1;
3. сколько инверсий в перестановке \: 0 и 1, так как 2 > 1;
4. соотвествующие произведения. \ и \

В итоге получаем:

\

Проанализировав ранее сказанное, получаем типовой алгоритм для нахождения определителя матрицы 2-го порядка 2х2:

\

Если рассмотреть данную формулу на наглядном примере, то это будет вот так:

Пример

Вычислить определитель матрицы \:

\

Решение:

Итак, у нас получается \.

Для решения необходимо воспользоваться ранее рассмотренной формулой:

\

Подставляем числа с примера и находим:

\

Ответ:

Определитель матрицы второго порядка = 21.

Чтобы упростить понимание процесса, как в данном случае находится определитель матрицы, можно представить такой расчёт: от произведения элементов основной диагонали отнимается произведение элементов другой диагонали.

\

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Что такое детерминант?

Это скалярное значение, которое получается из элементов квадратной матрицы и имеет определенные свойства линейного преобразования, описываемого матрицей. определитель матрицы калькулятор положительный или отрицательный, в зависимости от того, сохраняет ли линейное преобразование ориентацию векторного пространства или меняет ее на обратное. Это помогает нам найти обратную матрицу, а также то, что полезно в системах линейных уравнений, исчислении и многом другом. Он обозначается как det (A), det A или | A |.

Заметка:

Матрицы заключены в квадратные скобки, а определители обозначены вертикальными чертами. Матрица – это массив чисел, но определитель – одно число.

Как использовать этот онлайн-калькулятор определителя матрицы:

Наш онлайн-калькулятор помогает найти определитель матрицы калькулятор размером до 5×5 пятью различными методами. Просто следуйте пунктам для получения точных результатов.
Читать дальше!

Входы:

• Прежде всего, выберите порядок матрицы из выпадающего списка калькулятора.
• Затем введите значения матрицы в соответствующие поля.
• Затем выберите метод, с помощью которого вы найдете определитель.
• Наконец, нажмите кнопку “Рассчитать”.

Заметка:

Есть поле «номер столбца или строки», в которое вы вводите номер строки или номер столбца, которые необходимо развернуть. Кроме того, в нем есть поля для создания матрицы и очистки матрицы, он автоматически сгенерирует матрицу и очистит все значения из матрицы соответственно.

Выходы:

После заполнения всех полей калькулятор показывает:

• Определитель матрицы.
• Пошаговые расчеты.

Заметка:

Независимо от того, какой метод вы выберете для расчетов, онлайн-калькулятор определителя покажет вам результаты в соответствии с выбранным вариантом.

Вычисление определителя матрицы методом Гаусса.

Опишем суть этого метода. Матрица А с помощью элементарных преобразований приводится к такому виду, чтобы в первом столбце все элементы, кроме стали нулевыми (это сделать всегда возможно, если определитель матрицы А отличен от нуля). Эту процедуру опишем чуть позже, а сейчас поясним, для чего это делается. Нулевые элементы получаются для того, чтобы получить самое простое разложение определителя по элементам первого столбца. После такого преобразования матрицы А, учитывая восьмое свойство и , получим
где — минор (n-1)-ого порядка, получающийся из матрицы А вычеркиванием элементов ее первой строки и первого столбца.

С матрицей, которой соответствует минор , проделывается такая же процедура получения нулевых элементов в первом столбце. И так далее до окончательного вычисления определителя.

Теперь осталось ответить на вопрос: «Как получать нулевые элементы в первом столбце»?

Опишем алгоритм действий.

Если , то к элементам первой строки матрицы прибавляются соответствующие элементы k-ой строки, в которой . (Если все без исключения элементы первого столбца матрицы А нулевые, то ее определитель равен нулю по второму свойству и не нужен никакой метод Гаусса). После такого преобразования «новый» элемент будет отличен от нуля. Определитель «новой» матрицы будет равен определителю исходной матрицы в силу седьмого свойства.

Теперь мы имеем матрицу, у которой . При к элементам второй строки прибавляем соответствующие элементы первой строки, умноженные на , к элементам третьей строки – соответствующие элементы первой строки, умноженные на . И так далее. В заключении к элементам n-ой строки прибавляем соответствующие элементы первой строки, умноженные на . Так будет получена преобразованная матрица А, все элементы первого столбца которой, кроме , будут нулевыми. Определитель полученной матрицы будет равен определителю исходной матрицы в силу седьмого свойства.

Разберем метод при решении примера, так будет понятнее.

Пример.

Вычислить определитель матрицы порядка 5 на 5 .

Решение.

Воспользуемся методом Гаусса. Преобразуем матрицу А так, чтобы все элементы ее первого столбца, кроме , стали нулевыми.

Так как изначально элемент , то прибавим к элементам первой строки матрицы соответствующие элементы, например, второй строки, так как :

Знак « ~ » означает эквивалентность.

Теперь прибавляем к элементам второй строки соответствующие элементы первой строки, умноженные на , к элементам третьей строки – соответствующие элементы первой строки, умноженные на , и аналогично действуем вплоть до шестой строки:

Получаем

С матрицей проводим ту же процедуру получения нулевых элементов в первом столбце:

Следовательно,

Сейчас выполняем преобразования с матрицей :

Получаем

Матрица уже имеет необходимый вид, поэтому

Ответ:

.

Рассмотрим решение еще одного примера, но подробно описывать действия не будем. Это некоторый образец краткой записи вычисления определителя матрицы методом Гаусса.

Пример.

Вычислите определитель матрицы порядка 7 на 7.

Решение.

Следовательно,

Замечание.

На некотором этапе преобразования матрицы по методу Гаусса может возникнуть ситуация, когда все элементы нескольких последних строк матрицы станут нулевыми. Это будет говорить о равенстве определителя нулю.

Подведем итог.

Определителем квадратной матрицы, элементы которой есть числа, является число. Мы рассмотрели три способа вычисления определителя:

1. через сумму произведений сочетаний элементов матрицы;
2. через разложение определителя по элементам строки или столбца матрицы;
3. методом приведения матрицы к верхней треугольной (методом Гаусса).

Были получены формулы для вычисления определителей матриц порядка 2 на 2 и 3 на 3.

Мы разобрали свойства определителя матрицы. Некоторые из них позволяют быстро понять, что определитель равен нулю.

При вычислении определителей матриц порядка выше 3 на 3 целесообразно использовать метод Гаусса: выполнить элементарные преобразования матрицы и привести ее к верхней треугольной. Определитель такой матрицы равен произведению всех элементов, стоящих на главной диагонали.

Некогда разбираться?

Нахождение определителя

Результатом нахождение определителя матрицы является обычное число. Давайте рассмотрим самые популярные варианты.

Второй порядок

Пожалуй, это самая легкая задача. Чтобы найти определитель матрицы “два на два” пользуемся формулой ниже:

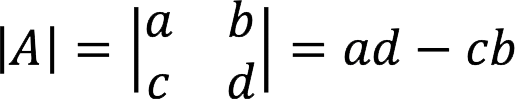
Пример 1:

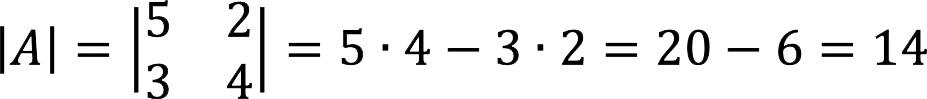
Пример 2:

Примечание: Не забываем обращать внимание на знаки элементов матрицы и учитывать их в расчетах

Третий порядок

Для вычисления определителя матрицы “три на три” следует использовать такую формулу:

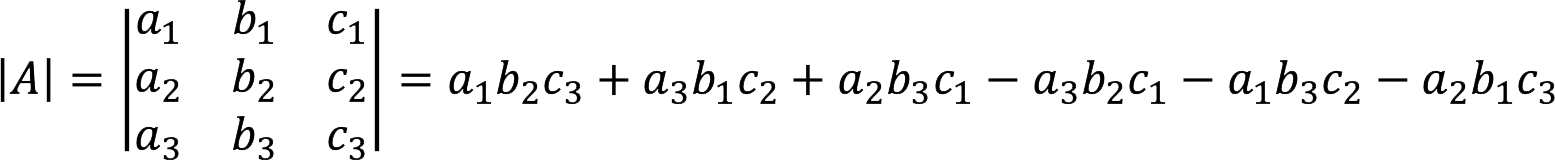
Пример:

|A| = 3 ⋅ 4 ⋅ 3 + (-1) ⋅ 6 ⋅ (-6) + 2 ⋅ 2 ⋅ 9 – (-1) ⋅ 4 ⋅ 9 – 3 ⋅ 2 ⋅ (-6) – 2 ⋅ 6 ⋅ 3 = 144.

Как мы видим, формула длинная, и запомнить ее достаточно сложно. Но есть специальное правило Саррюса (или метод параллельных полосок), благодаря которому ничего запоминать не нужно. Вот, в чем оно заключается.

С правой стороны от определителя мы дописываем первый и второй столбцы, затем проводим линии, как показано на рисунке ниже.

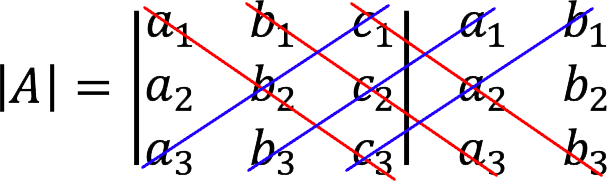
Множители, расположенные на диагоналях красного цвета в формуле участвуют со знаком “плюс”, синего цвета – со знаком минус.

Как мы видим, это те же самые множители, что и в первой формуле, но переставленные местами, что на результат не влияет. Таким образом, используя метод Саррюса, можно значительно снизить риск допущения ошибки в процессе выполнения расчетов.

Геометрическое определение

Прежде всего хотел бы отметить, что определитель существует только для квадратных матриц вида $\left$. Определитель — это число, которое cчитается по определённым правилам и является одной из характеристик этой матрицы (есть другие характеристики: ранг, собственные вектора, но об этом в других уроках).

Ну и что это за характеристика? Что он означает? Всё просто:

На первый взгляд это определение может показаться совершенно неадекватным. Но давайте не будем спешить с выводами — глянем на примеры. На самом деле всё элементарно, Ватсон:

Небольшое замечание по поводу системы обозначений. Кому-то наверняка не понравится, что я игнорирую «стрелочки» над векторами. Якобы так можно спутать вектор с точкой или ещё с чем.

Но давайте серьёзно: мы с вами уже взрослые мальчики и девочки, поэтому из контекста прекрасно понимаем, когда речь идёт о векторе, а когда — о точке. Стрелки лишь засоряют повествование, и без того под завязку напичканное математическими формулами.

И ещё. В принципе, ничто не мешает рассмотреть и определитель матрицы 1×1 — такая матрица представляет собой просто одну клетку, а число, записанное в этой клетке, и будет определителем

Но тут есть важное замечание:

И если вы хотите получить объём в классическом смысле этого слова, придётся взять модуль определителя, но сейчас не стоит париться об этом — всё равно через несколько секунд мы научимся считать любой определитель с любыми знаками, размерами и т.д.:)