Как найти обратную матрицу методом гаусса

Обращение блочных матриц

Т

Теорема .. Пусть имеется блочная квадратная матрица вида

$$
\left(
\begin{array}{rr}
A & B \\
C & D
\end{array}
\right) \quad ,
$$
где матрица $ A_{} $ — квадратная порядка $ k_{} $, а матрица $ D_{} $ — квадратная порядка $ \ell_{} $. Тогда
$$\left(
\begin{array}{rr}
A & B \\
C & D
\end{array}
\right)^{-1}=
\left(
\begin{array}{cc}
A^{-1} +A^{-1}BK^{-1}CA^{-1} & -A^{-1}BK^{-1} \\
-K^{-1}CA^{-1} & K^{-1}
\end{array}
\right) \ ,
$$
где матрица
$$ K=D-CA^{-1}B $$
называется шуровским дополнениемк подматрице $ A_{} $. Здесь предполагается, что матрицы $ A_{} $ и $ K_{} $ — неособенные.

=>

При $ B=\mathbb O $
имеем:

$$
\left(
\begin{array}{rr}
A & \mathbb O \\
C & D
\end{array}
\right)^{-1}=
\left(
\begin{array}{cc}
A^{-1} & \mathbb O \\
-D^{-1}CA^{-1} & D^{-1}
\end{array}
\right) \ ,
$$
если матрицы $ A_{} $ и $ D_{} $ — неособенные.

Доказательство. Будем искать
$$
\left(
\begin{array}{rr}
A & \mathbb O \\
C & D
\end{array}
\right)^{-1}
$$
в виде
$$
\left(
\begin{array}{rr}
X & Y \\
U & V
\end{array}
\right)_{n\times n}
$$
при $ k\times k $-матрице $ X $ и $ \ell\times \ell $-матрице $ V $. Разбиваем
матричное равенство
$$
\left(
\begin{array}{rr}
X & Y \\
U & V
\end{array}
\right)
\left(
\begin{array}{rr}
A & \mathbb O \\
C & D
\end{array}
\right)
=\left(
\begin{array}{rr}
E_k & \mathbb O \\
\mathbb O & E_{\ell}
\end{array}
\right)
$$
на четыре отдельных
$$
\begin{array}{cc}
XA+YC=E_k, & YD=\mathbb O, \\
UA+VC=\mathbb O, & VD=E_{\ell}
\end{array}
\quad \Rightarrow \quad
\begin{array}{l}
Y=\mathbb O, \\
V=D^{-1}.
\end{array}
$$
Подставляем полученное в два оставшихся равенства: $ X=A^{-1} $, $ U=-D^{-1}CA^{-1} $.

Теорема Фробениуса имеет, в основном, теоретическое значение — за исключением одного частного случая, когда матрица $ D_{} $ имеет порядок 1, т.е. является числом. Пусть, например, уже найдена обратная матрица для матрицы
$$ A =
\left(
\begin{array}{llll}
a_{11} & \dots & a_{1n} \\
a_{21} & \dots & a_{2n} \\
\vdots & & \vdots \\
a_{n1} & \dots & a_{nn}
\end{array}
\right)
$$
порядка $ n_{} $ и ставится задача нахождения обратной матрицы для ее матрицы
$$
\left(
\begin{array}{rr}
A & B \\
C & D
\end{array}
\right) =
\left(
\begin{array}{llll}
a_{11} & \dots & a_{1n} & a_{1,n+1} \\
a_{21} & \dots & a_{2n} & a_{2,n+1} \\
\vdots & && \vdots \\
a_{n1} & \dots & a_{nn} & a_{n,n+1} \\
a_{n+1,1} & \dots & a_{n+1,n} & a_{n+1,n+1}
\end{array}
\right)
$$
порядка $ n+1_{} $. Тогда из теоремы следует:
$$
\left(
\begin{array}{rr}
A & B \\
C & D
\end{array}
\right)^{-1}=
\frac{1}{\kappa}
\left(
\begin{array}{cc}
A^{-1}(\kappa E+BCA^{-1}) & -A^{-1}B \\
-CA^{-1} & 1
\end{array}
\right) ;
$$
здесь $ E_{} $ — единичная матрица порядка $ n_{} $, а число
$$
\kappa=a_{n+1,n+1}-CA^{-1}B=\underbrace{a_{n+1,n+1}}_D-\underbrace{\left( a_{n+1,1} , \dots , a_{n+1,n} \right)}_CA^{-1}
\underbrace{\left(\begin{array}{l}
a_{1,n+1} \\
a_{2,n+1} \\
\vdots \\
a_{n,n+1}
\end{array}
\right)}_B
$$
очевидно связано с определителем новой матрицы:
$$
\det\left(
\begin{array}{rr}
A & B \\
C & D
\end{array}
\right)= \kappa \det A \ .
$$
Этот метод обращения матрицы известен в литературе как метод окаймления, он подробно изложен в .

?

Найти обратную матрицу для матрицы Фробениуса

$$
{\mathfrak F}=
\left( \begin{array}{lllllll}
0 & 1 & 0 & 0 & \dots & 0 & 0 \\
0 & 0 & 1 & 0 & \dots & 0 & 0 \\
0 & 0 & 0 & 1 & \dots & 0 & 0 \\
\dots& &&&\ddots & & \dots \\
0 & 0 & 0 & 0 & \dots & 0 & 1 \\
a_n & a_{n-1} & a_{n-2} & & \dots & a_2 & a_1
\end{array} \right)_{n \times n}
$$

Решение и ответ

☞

ЗДЕСЬ

=>

Если матрица $ A $ имеет следующую структуру

$$
A=\left( \begin{array}{ccccc}
a_{11} & a_{12} & \dots & a_{1n} \\
0 & a_{22} & \dots & a_{2n} \\
0 & a_{32} & \dots & a_{3n} \\
\vdots & \vdots & & \vdots \\
0 & a_{n2} & \dots & a_{nn}
\end{array}
\right)
$$
при $ a_{11} \ne 0 $ и невырожденной подматрице
$$
\widetilde A=
\left( \begin{array}{cccc}
a_{22} & \dots & a_{2n} \\
a_{32} & \dots & a_{3n} \\
\vdots & & \vdots \\
a_{n2} & \dots & a_{nn}
\end{array}
\right) \, ,
$$
то
$$
A^{-1}=
\left[ \begin{array}{cc}
1/a_{11} & B \widetilde A^{-1} \\
0 & \widetilde A^{-1}
\end{array}
\right] \quad \mbox{при} \ B:=-\frac{1}{a_{11}} \, .
$$

Этот результат позволяет организовать вычисление обратной матрицы для верхнетреугольной последовательным вычислением обратных к ее подматрицам из правого нижнего угла:
$$
a_{nn}^{-1} \ \rightarrow \
\left( \begin{array}{cc}
a_{n-1,n-1} & a_{n-1,n} \\
0 & a_{nn}
\end{array}
\right)^{-1}
\ \rightarrow \
\left( \begin{array}{ccc}
a_{n-2,n-2} & a_{n-2,n-1} & a_{n-2,n} \\
0 & a_{n-1,n-1} & a_{n-1,n} \\
0 & 0 & a_{nn}
\end{array}
\right)^{-1}
\ \rightarrow \dots
$$

Основные понятия

Под матрицей в линейной алгебре понимается прямоугольный массив элементов (таблица). Ниже представлены наборы элементов, заключенные в круглые скобки. Это и есть матрицы. Из приведенного примера видно, что элементами в прямоугольных массивах являются не только числа. Матрица может состоять из математических функций, алгебраических символов.

Для того чтобы разобраться с некоторыми понятиями, составим матрицу A из элементов a_ij. Индексы являются не просто буквами: i – это номер строки в таблице, а j – это номер столбца, в области пересечения которых располагается элемент a_ij. Итак, мы видим, что у нас получилась матрица из таких элементов, как a₁₁, a₂₁, a₁₂, a₂₂ и т. д. Буквой n мы обозначили число столбцов, а буквой m – число строк. Символ m × n обозначает размерность матрицы. Это то понятие, которое определяет число строк и столбцов в прямоугольном массиве элементов.

Необязательно в матрице должно быть несколько столбцов и строк. При размерности 1 × n массив элементов является однострочным, а при размерности m × 1 – одностолбцовым. При равенстве числа строчек и числа столбцов матрицу именуют квадратной. У каждой квадратной матрицы есть определитель (det A). Под этим термином понимается число, которое ставится в соответствие матрице A.

Еще несколько важных понятий, которые нужно запомнить для успешного решения матриц, – это главная и побочная диагонали. Под главной диагональю матрицы понимается та диагональ, которая идет вниз в правый угол таблицы из левого угла сверху. Побочная диагональ идет в правый угол вверх из левого угла снизу.

Вычисление обратной матрицы

1. Вычисляем определитель матрицы.
2. Записываем транспонированную матрицу.
3. Заменяем каждый элемент транспонированной матрицы его алгебраическим дополнением. Полученная матрица является присоединённой матрицей.
4. Вычисляем обратную матрицу.

Пример 46 $A=\begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}$

$\left|A\right|=1\cdot 5-6=-1$ Матрица обратима, значит, можно найти обратную ей матрицу.

$ A^{T}= \begin{pmatrix} 1 & 2\\ 3 & 5 \end{pmatrix}$

Заменяем элементы транспонированной матрицы их алгебраическими дополнениями.

$1\longrightarrow (-1)^{1+1}\cdot \Delta_{1,1}=(-1)^{2}\cdot5 = 5$ $2\longrightarrow (-1)^{1+2}\cdot \Delta_{1,2}=(-1)^{3}\cdot3 = -3$ $3\longrightarrow (-1)^{2+1}\cdot \Delta_{2,1}=(-1)^{3}\cdot2 = -2$ $5\longrightarrow (-1)^{2+2}\cdot \Delta_{2,2}=(-1)^{4}\cdot1 = 1$

$adj(A)= \begin{pmatrix} 5 & -3\\ -2 & 1\\ \end{pmatrix}$

$A^{-1}=- \begin{pmatrix} 5 & -3\\ -2 & 1 \end{pmatrix} = \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}$

Пример 47 $B=\begin{pmatrix} 2 & -7\\ -1 & 6 \end{pmatrix}$

$\left|B\right|=2\cdot 6-(-7)\cdot (-1) = 5$

Матрица обратима, значит, можно найти обратную ей матрицу. $A^{T}= \begin{pmatrix} 2 & -1\\ -7 & 6 \end{pmatrix}$

Заменяем элементы транспонированной матрицы их алгебраическими дополнениями. $2\longrightarrow (-1)^{1+1}\cdot \Delta_{1,1}=(-1)^{2}\cdot6 = 6$ $-1\longrightarrow (-1)^{1+2}\cdot \Delta_{1,2}=(-1)^{3}\cdot(-7) = 7$ $-7\longrightarrow (-1)^{2+1}\cdot \Delta_{2,1}=(-1)^{3}\cdot(-1) = 1$ $6\longrightarrow (-1)^{2+2}\cdot \Delta_{2,2}=(-1)^{4}\cdot2 = 2$

$adj(A)= \begin{pmatrix} 6 & 7\\ 1 & 2 \end{pmatrix}$

$A^{-1}=\frac{1}{5} \begin{pmatrix} 6 & 7\\ 1 & 2 \end{pmatrix} = \begin{pmatrix} \frac{6}{5} & \frac{7}{5}\\ \frac{1}{5} & \frac{2}{5} \end{pmatrix}$

Пример 48 $C=\begin{pmatrix} 1 & 3 & 2\\ 4 & 1 & 1\\ 1 & 2 & 3\\ \end{pmatrix}$

Вычисляем определитель по известной формуле и получаем $\left|B\right|=-18$.

Матрица обратима, значит, можно найти обратную ей матрицу. $C^{T}=\begin{pmatrix} 1 & 4 & 1\\ 3 & 1 & 2\\ 2 & 1 & 3 \end{pmatrix}$

Заменяем каждый элемент транспонированной матрицы его алгебраическим дополнением. $ 1\longrightarrow (-1)^{1+1}\cdot \Delta_{1,1}=(-1)^{2}\cdot \begin{vmatrix} 1 & 2\\ 1 & 3 \end{vmatrix} = 3 — 2 = 1$

$4\longrightarrow (-1)^{1+2}\cdot \Delta_{1,2}=(-1)^{3}\cdot \begin{vmatrix} 3 & 2\\ 2 & 3 \end{vmatrix} = -(9-4)=-5$

$1\longrightarrow (-1)^{1+3}\cdot \Delta_{1,3}=(-1)^{4}\cdot \begin{vmatrix} 3 & 1\\ 2 & 1 \end{vmatrix} = 3-2=1$

$3\longrightarrow (-1)^{2+1}\cdot \Delta_{2,1}=(-1)^{3}\cdot \begin{vmatrix} 4 & 1\\ 1 & 3\\ \end{vmatrix} = -(12-1)=-11$

$1\longrightarrow (-1)^{2+2}\cdot \Delta_{2,2}=$ $(-1)^{4}\cdot\begin{vmatrix} 1 & 1\\ 2 & 3\\ \end{vmatrix}=3-2=1$

$2\longrightarrow (-1)^{1+3}\cdot \Delta_{2,3}=$ $(-1)^{5}\cdot\begin{vmatrix} 1 & 4\\ 2 & 1 \end{vmatrix}= -(1-8)=7$

$2\longrightarrow (-1)^{3+1}\cdot \Delta_{3,1}=$ $(-1)^{4}\cdot\begin{vmatrix} 4 & 1\\ 1 & 2 \end{vmatrix}=8-1=7$

$1\longrightarrow (-1)^{3+2}\cdot \Delta_{3,2}=$ $(-1)^{5}\cdot \begin{vmatrix} 1 & 1\\ 3 & 2 \end{vmatrix}=-(2-3)=1$

$3\longrightarrow (-1)^{3+3}\cdot \Delta_{3,3}=$ $(-1)^{6}\cdot\begin{vmatrix} 1 & 4\\ 3 & 1 \end{vmatrix}=1-12=-11$

$adj(A)= \begin{pmatrix} 1 & -5 & 1\\ -11 & 1 & 7\\ 7 & 1 & -11 \end{pmatrix}$

$A^{-1} = — \frac{1}{18}\cdot \begin{pmatrix} 1 & -5 & 1\\ -11 & 1 & 7\\ 7 & 1 & -11 \end{pmatrix} =$ $\begin{pmatrix} — \frac{1}{18} & \frac{5}{18} & -\frac{1}{18}\\ \frac{11}{18} & -\frac{1}{18} & -\frac{7}{18}\\ -\frac{7}{18} & -\frac{1}{18} & \frac{11}{18} \end{pmatrix}$

Параметры сверточного слоя

Размеры входного и выходного изображения

• srcC / dstC — число каналов во входном и выходном изображении. Альтернативные обозначения: C / D.
• srcH / dstH — высота входного и выходного изображения. Альтернативное обозначение: H.
• srcW / dstW — ширина входного и выходного изображения. Альтернативное обозначение: W.
• batch — число входных (выходных) изображений — слой за раз может обработать целую партию изображений. Альтернативное обозначение: N.

Размеры ядра свертки

• kernelY — высота ядра свертки. Альтернативное обозначение: Y.
• kernelX — ширина ядра свертки. Альтернативное обозначение: X.

1×13×35×57×7

• strideY — вертикальный шаг свертки.
• strideX — горизонтальный шаг свертки.

1×12×2

• dilationY — вертикальное растяжение свертки.
• dilationX — горизонтальное растяжение свертки.

1×1

Паддинг входного изображения

kernel — 1

• padY / padX — передние вертикальный и горизонтальный отступы.
• padH / padW — задние вертикальный и горизонтальный отступы.

Что такое массив перестановок

Последние несколько строк вывода на рис. 1 указывают, что матрицы L и U можно перемножить так, чтобы получить исходную матрицу. Знание того, как это делается, не поможет вам в решении практических задач операций над матрицами, но позволит разобраться, что представляет собой часть P в разложении LUP. Восстановление исходной матрицы из ее компонентов L и U также пригодится для тестирования ваших библиотечных методов работы с матрицами на согласованность.

Один из способов восстановления исходной матрицы после разложения LUP — перемножение L и U с последующей перестановкой строк результата на основе массива P:

Метод UnPermute можно закодировать так:

Второй подход — преобразование массива perm в матрицу perm с последующим перемножением матрицы perm и комбинированной матрицы LU:

Матрица perm является квадратной с одним значением 1.0 в каждой строке и каждом столбце. Метод, который создает матрицу perm из массива perm, можно написать следующим образом:

Решение системы линейных уравнений по формулам Крамера

Чтобы решить систему линейных уравнений методом Крамера, нужно познакомиться с понятием определителя.

Определение

Определителем системы называют запись чисел в квадратной таблице, в соответствие которой ставится число по некоторому правилу.

Давайте познакомимся с этим правилом. Пусть даны четыре числа a, b, c, d. Пусть они имеют следующее расположение в квадратной таблице:

Значение определителя системы в этом случае находится по формуле:

Определитель, составленный из коэффициентов при переменных в линейной системе уравнений, называется главным определителем системы. Будем обозначать его Δ. Например, у рассмотренной выше системы уравнений:

главный определитель будет иметь вид:

Найдём его значение:

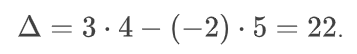
Для решения системы линейных уравнений методом Крамера нам понадобятся ещё два определителя, которые называются вспомогательными:

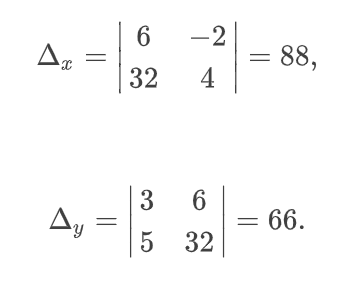
Отметим, что в данные определители уже входят правые части каждого уравнения системы. Так, в определитель Δₓ первым столбцом записываем правые части уравнений (так называемые свободные члены уравнений), второй столбец оставляем таким же, как в главном определителе системы. В определитель Δу вторым столбцом записываем правые части уравнений, а первый столбец оставляем таким же, как в главном определителе системы.

Итак, формулы Крамера для решения системы двух линейных уравнений с двумя переменными: 

Отметим, что данный метод решения СЛАУ можно применять лишь в тех случаях, когда Δ ≠ 0.

Убедимся в том, что данные формулы работают, подставив в них ранее найденные значения определителей:

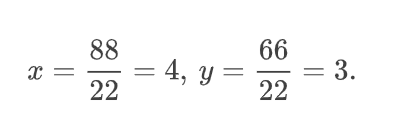
Пара чисел (4;3) действительно является решением данной системы уравнений.

Обобщим алгоритм нахождения решений системы двух линейных уравнений с двумя переменными методом Крамера. Пусть дана система линейных уравнений: 

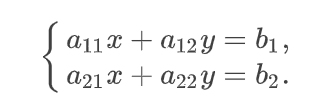
Нужно: 

1. Вычислить главный определитель системы

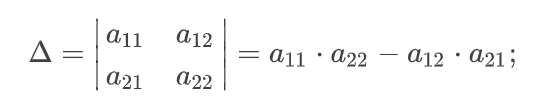
2. Вычислить вспомогательные определители

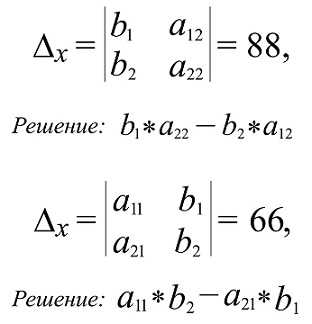
Объем параллелепипеда

Связь между определителем и объемом не очевидна, однако мы можем предположить для начала, что все углы прямые, т. е. грани взаимно перпендикулярны, и мы имеем дело с прямоугольным параллелепипедом. Тогда объем его равен просто произведению длин ребер .

Мы хотим получить ту же самую формулу с помощью определителя. С этой целью вспомним, что ребра параллелепипеда представляются строками матрицы . В нашем случае эти строки
взаимно ортогональны, так что

Величины суть квадраты длин строк матрицы, т. е. квадраты длин ребер, и нули вне диагонали получаются вследствие ортогональности строк. Переходя к определителям, получаем

Извлекая корень, мы и приходим к требуемому соотношению:
определитель равняется объему. Знак при будет зависеть от того, образуют ребра правостороннюю систему координат вида или левостороннюю .

Если область не прямоугольна, то объем уже не равен произведению длин ребер. В плоском случае «объем» параллелограмма равен произведению длины основания на высоту .

Вектор длины есть разность между вектором второй строки и его проекцией на вектор первой строки.

Площадь паралелограмма равна .

Площади квадрата и параллелограмма.

Первый представляет собой единичный квадрат, и его площадь, равна 1. Второй есть параллелограмм с единичными основанием и высотой; его площадь не зависит от «сдвига», даваемого коэффициентом , и равна 1.

Разложение матрицы

Продукты и технологии:

C#, Microsoft .NET Framework

В статье рассматриваются:

• реализация матрицы на C#;
• распараллеливание перемножения матриц;
• подходы к разложению матрицы;
• использование разложения матрицы для обращения матрицы (matrix inversion);
• вычисление определителя матрицы (determinant of a matrix).

Разложение матрицы — это метод разбиения квадратной числовой матрицы на две разные квадратные матрицы, лежащий в основе эффективного решения системы уравнений, которое в свою очередь является основой для обращения матрицы. Обращение матрицы — часть многих важных алгоритмов. В этой статье представлен и поясняется код на C#, выполняющий разложение матрицы, обращение матрицы, решение системы уравнений и связанные операции.

Следует отметить, что важным пополнением вашей персональной библиотеки кода является не само по себе разложение матрицы, а набор матричных методов. Я объясняю эти методы, поэтому вы сможете модифицировать исходный код под свои потребности. Кроме того, некоторые приемы, используемые в матричных методах, можно повторно задействовать в других сценариях кодирования.

Лучший способ прочувствовать то, о чем пойдет речь в этой статье, — взглянуть на экранный снимок на рис. 1. Демонстрационная программа начинает с создания квадратной матрицы 4 × 4 и отображения ее значений. Затем матрица раскладывается в так называемую матрицу LUP (lower, upper, permutation) (нижняя часть, верхняя часть и часть, относящаяся к перестановке). Последняя часть представляет собой массив со значениями {3,1,2,0} и указывает, что строки 0 и 3 поменялись местами в процессе разложения. В этом процессе также было сгенерировано значение-переключатель (toggle value), равное –1, сообщающее, что выполнено нечетное количество перестановок строк. Эта программа демонстрирует разложение двумя способами: сначала в комбинированную матрицу LU, а затем в отдельные матрицы L и U. Далее программа вычисляет и отображает обращенную по отношению к исходной матрицу, используя «за кулисами» матрицу LUP. Демонстрационная программа вычисляет определитель исходной матрицы, вновь применяя разложение. Далее она использует обратную матрицу для решения системы линейных уравнений и завершает свою работу объединением матриц L и U в исходную матрицу.

Рис. 1. Демонстрация разложения матрицы

К чему все эти сложности с созданием собственного метода разложения матрицы и библиотеки связанных методов? Хотя существует множество автономных матричных инструментов, их иногда очень трудно интегрировать в приложение или систему

Несмотря на фундаментальную важность разложения матрицы, доступно всего несколько бесплатных реализаций в .NET-коде, не защищенных авторским правом; однако в них нет детальных пояснений, которые позволили бы вам модифицировать этот исходный код под свои потребности

Нахождение обратной матрицы с помощью элементарных преобразований (метод Гаусса)

Пример 3. Методом элементарных преобразований вычислить -1 если = .

Решение. Приписываем к исходной справа единичную того же порядка: . С помощью элементарных преобразований столбцов приведём левую “половину” к единичной, совершая одновременно точно такие преобразования над правой «половиной».
Поменяем местами 1 со 2 столбцы: ~. К третьему прибавим первый, ко второму — первый, × на -2: . Из первого вычтем удвоенный второй, из третьего — × на 6 второй; . Прибавим третий к первому и второму: . Умножим последний на минус один: . Справа от вертикальной черты квадратная таблица размером 3х3 .

характеристики

Свойства группы

Набор регулярных матриц фиксированного размера над унитарным кольцом вместе с умножением матриц в качестве зацепления образует (обычно некоммутативную ) группу , общую линейную группу . В этой группе единичная матрица является нейтральным элементом, а обратная матрица — обратным элементом . Таким образом, ясно определена инверсия матрицы, а также левая и правая инверсия. В частности, обращение к единичной матрице снова приводит к единичной матрице, то есть
Р.{\ displaystyle R} GL⁡(п,Р.){\ Displaystyle \ OperatorName {GL} (п, R)}

Я.-1знак равноЯ.{\ displaystyle I ^ {- 1} = I},

и инверсия обратной матрицы снова является выходной матрицей, то есть

(А.-1)-1знак равноА.{\ Displaystyle \ влево (А ^ {- 1} \ вправо) ^ {- 1} = А}.

Поэтому матрицы и также называются обратными друг другу. Произведение двух регулярных матриц снова является правильным, а обратное произведение является произведением соответствующего обратного, но в обратном порядке:
А.{\ displaystyle A}А.-1{\ displaystyle A ^ {- 1}}

(А.⋅Б.)-1знак равноБ.-1⋅А.-1{\ Displaystyle \ влево (A \ cdot B \ right) ^ {- 1} = B ^ {- 1} \ cdot A ^ {- 1}}.

Если матрицу можно представить как произведение легко обратимых матриц, то таким образом можно быстро определить обратную матрицу. Общая формула произведения применяется к обратному произведению нескольких матриц.

(А.1⋅А.2⋯А.k)-1знак равноА.k-1⋯А.2-1⋅А.1-1{\ displaystyle \ left (A_ {1} \ cdot A_ {2} \ dotsm A_ {k} \ right) ^ {- 1} = A_ {k} ^ {- 1} \ dotsm A_ {2} ^ {- 1 } \ cdot A_ {1} ^ {- 1}}

с . Это особенно относится к обратной матрице степениk∈N{\ Displaystyle к \ в \ mathbb {N}}

(А.k)-1знак равно(А.-1)k{\ displaystyle \ left (A ^ {k} \ right) ^ {- 1} = \ left (A ^ {- 1} \ right) ^ {k}}.

Эта матрица также отмечена.
А.-k{\ displaystyle A ^ {- k}}

Прочие свойства

Следующие дополнительные свойства применяются к обратной матрице с записями из тела . Верно
обратное к произведению матрицы на скаляр сK{\ displaystyle K}c∈K{\ displaystyle c \ in K}c≠{\ displaystyle c \ neq 0}

(cА.)-1знак равноc-1А.-1{\ Displaystyle (СА) ^ {- 1} = с ^ {- 1} А ^ {- 1}}.

Обратная транспонированная матрица равна транспонированной обратной, поэтому

(А.Т)-1знак равно(А.-1)Т{\ displaystyle \ left (A ^ {T} \ right) ^ {- 1} = \ left (A ^ {- 1} \ right) ^ {T}}.

То же самое относится и к обратной к присоединенной комплексной матрице

(А.ЧАС)-1знак равно(А.-1)ЧАС{\ displaystyle \ left (A ^ {H} \ right) ^ {- 1} = \ left (A ^ {- 1} \ right) ^ {H}}.

Эти две матрицы также иногда записываются через и . Относится к в ранге обратного
А.-Т{\ displaystyle A ^ {- T}}А.-ЧАС{\ displaystyle A ^ {- H}}

классифицировать⁡(А.-1)знак равноклассифицировать⁡(А.)знак равноп{\ displaystyle \ operatorname {rank} \ left (A ^ {- 1} \ right) = \ operatorname {rank} (A) = n}

и для его определителя

Det⁡(А.-1)знак равно(DetА.)-1{\ displaystyle \ operatorname {det} \ left (A ^ {- 1} \ right) = (\ det A) ^ {- 1}}.

Если собственное от того, является к собственному вектору , то собственное число является также собственным вектором .
λ{\ displaystyle \ lambda}А.{\ displaystyle A} Икс{\ displaystyle x}λ-1{\ displaystyle \ lambda ^ {- 1}}А.-1{\ displaystyle A ^ {- 1}}Икс{\ displaystyle x}

Инварианты

Некоторые обычные матрицы сохраняют свои пользовательские свойства при инверсии. Примеры этого:

• верхние и нижние треугольные матрицы, а также строго верхние и нижние треугольные матрицы
• положительно определенные и отрицательно определенные матрицы
• симметричные , персимметричные , бисимметричные и центрально-симметричные матрицы
• унимодулярные и целочисленные унимодулярные матрицы

Решение задач методом Гаусса

Пример

Найти инверсию матрицы третьего порядка:

\(A=\begin{pmatrix}2&3&7\\1&-5&2\\3&-1&9\end{pmatrix}\)

Решение:

1. Запишем справа от A единичную диагональную матрицу:

\(\left(\begin{array}{ccc}2&3&7\\1&-5&2\\3&-1&9\end{array}\left|\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right.\right)\)

Теперь необходимо выполнить преобразования, чтобы единичная диагональная матрица оказалась справа.

2. Первую и вторую строку поменяем местами:

\(\left(\begin{array}{ccc}1&-5&2\\2&3&7\\3&-1&9\end{array}\left|\begin{array}{ccc}0&1&0\\1&0&0\\0&0&1\end{array}\right.\right)\)

3. Вторую строку суммируем с первой, умноженной на −2. Третью строку сложим с первой, умноженной на −3:

\(\left(\begin{array}{ccc}1&-5&2\\0&13&3\\0&14&3\end{array}\left|\begin{array}{ccc}0&1&0\\1&-2&0\\0&-3&1\end{array}\right.\right)\)

4. Вторую сложим с третьей строкой, умноженной на −1:

\(\left(\begin{array}{ccc}1&-5&2\\0&-1&0\\0&14&3\end{array}\left|\begin{array}{ccc}0&1&0\\1&1&-1\\0&-3&1\end{array}\right.\right)\)

5. Выполним умножение второй строки на −1:

\(\left(\begin{array}{ccc}1&-5&2\\0&1&0\\0&14&3\end{array}\left|\begin{array}{ccc}0&1&0\\-1&-1&1\\0&-3&1\end{array}\right.\right)\)

6. Первую строку сложим с рядом чисел, полученных при умножении второй строки на 5. К третьей строке прибавим вторую строку, умноженную на −14:

\(\left(\begin{array}{ccc}1&0&2\\0&1&0\\0&0&3\end{array}\left|\begin{array}{ccc}-5&-4&5\\-1&-1&1\\14&11&-13\end{array}\right.\right)\)

7. Произведем деление третьей строки на 3:

\(\left(\begin{array}{ccc}1&0&2\\0&1&0\\0&0&1\end{array}\left|\begin{array}{ccc}-5&-4&5\\-1&-1&1\\\frac{14}3&\frac{11}3&\frac{-13}3\end{array}\right.\right)\)

8. Сложим первую строку с умноженной на −2 третьей:

\(\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\left|\begin{array}{ccc}\frac{-43}3&\frac{-34}3&\frac{41}3\\-1&-1&1\\\frac{14}3&\frac{11}3&\frac{-13}3\end{array}\right.\right)\)

Значит, инверсия матрицы A равна:

Как использовать матричный анализ

Метод матрицы решений работает так: вы составляете таблицу, где заголовками строк будет список вариантов из которых нужно сделать выбор, а заголовками столбцов будут факторы, которые нужно учесть. Далее вы оцениваете каждую комбинацию вариант/фактор, используя для этой оценки весовой коэффициент.. Затем полученные оценки суммируются для каждого варианта решения и вы получаете общую оценку.

Может звучать несколько сложно, но данный метод довольно все же прост в использовании. Рассмотрим пошаговое руководство с примером.

Шаг 1

Запишите все ваши варианты решений в первой колонке таблицы в качестве названий строк таблицы, и перечислите факторы, которые нужно рассмотреть, в качестве названий столбцов. Например, если вы покупаете новый ноутбук, факторами для рассмотрения могут быть стоимость, размеры и емкость жесткого диска, вес, размер экрана и т.п.

Шаг 2

Теперь заполняйте ячейки вашей таблицы, оценивая каждый вариант выбора решения  для каждого фактора. Оценка варианта может находиться в пределах от 0 (плохо) до 5 (отлично). Заметим, что вы не обязаны проставлять разные оценки для каждого варианта – если ни один из них не подходит для конкретного фактора в вашем решении, то все они могут получить оценку 0.

Шаг 3

Следующим шагом является определение относительной важности факторов в принятии решения. Обозначьте ее числами, скажем от 0 до 5, где 0 означает, что данный фактор совершенно неважен для окончательного решения, а 5 означает, что он весьма важен. (Вполне допустимо иметь факторы с одинаковой важностью.)

(Вполне допустимо иметь факторы с одинаковой важностью.)

Шаг 4

Теперь нужно перемножить полученные на шаге 2 оценки с относительной важностью фактора, которую вы определили на шаге 3. Это даст вам взвешенные оценки для каждой комбинации вариант/фактор

Шаг 5

Наконец, сложите все взвешенные оценки для каждого из ваших вариантов решения. Тот вариант, который получит наибольшую сумму, выигрывает!

Как лучше разобраться в теме

С формулой матрицы, а также ее основными компонентами теперь все понятно. И с основными операциями тоже удалось познакомиться. Отныне с легкостью найдем матрицу даже в уравнении при необходимости.

Для того, чтобы лучше вникнуть в соответствующую тему, стоит хорошенько изучить школьный курс математики, а также алгебру на 1 курсе обучения в ВУЗах. Информация пригодится как ученым, так и программистам.

Научиться коддить можно на специализированных дистанционных курсах. Они помогут быстро вникнуть в основы математики и информатики, а также создания приложений и игр. Курс рассчитан на срок до года. В процессе даже новичок, далекий от точных наук, сможет разобраться с матрицами и коддингом. А еще человек получит бесценную практику и новые полезные знакомства.

Хотите освоить современную IT-специальность? Огромный выбор курсов по востребованным IT-направлениям есть в Otus!

Также, возможно, вам будет интересен следующий курс: