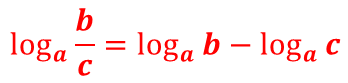Формулы и свойства логарифмов

Алгоритм решения неравенств с логарифмами

Кратко разберем общий алгоритм решения неравенств с логарифмами. Если хотите разобраться подробно, изучив все детали, листайте ниже. В общем виде логарифмическое неравенство можно записать так:
$$\log_{a}f(x) \gt \log_{a}g(x);$$
где \(a \gt 0, \quad a\neq1\) — основание логарифма;
\(f(x) \gt 0 \, ,g(x) \gt 0\) — какие-то выражения, зависящие от \(x\).

Логарифмы слева и справа от знака неравенства должны быть с одинаковым основанием! Только в этом случае можно избавиться от логарифмов и сравнить подлогарифмические функции

При этом важно следить за основанием, если \(a>1\), просто вычеркнем логарифмы и получим неравенство:
$$f(x) \gt g(x);$$. Мы рассмотрели случай только при основании логарифма \(a \gt 1\), а что будет, если \(0 \lt a \lt 1?\) Оказывается, в этом случае мы тоже избавляемся от логарифмов, но при этом обязательно меняем знак неравенства на противоположный!

Мы рассмотрели случай только при основании логарифма \(a \gt 1\), а что будет, если \(0 \lt a \lt 1?\) Оказывается, в этом случае мы тоже избавляемся от логарифмов, но при этом обязательно меняем знак неравенства на противоположный!

При \(0 \lt a \lt 1\) неравенство будет выглядеть так:
$$f(x) \lt g(x);$$

Логарифм: теоретический справочник

Определение	Формулы
Логарифмом числа по b основанию a называется такое число, обозначаемое $$ \log _a b$$ , что $$ a^{\log _a b} = b$$. a — основание логарифма: a > 0, $$ a \ne 1 $$, b — логарифмическое число: b > 0 Основное логарифмическое тождество: $$ a^{\log _a b} = b,a > 0,a \ne 1,b > 0$$	$$\quad $$ $$ \begin{array}{l} \log _a 1 = 0;\quad \;\log _a a = 1, \\ a > 0,a \ne 1;\;\;\lg 10 = \ln e = 1 \\ \end{array}$$	$$\quad $$ $$ \log _a a^k = k,k \in R$$
$$\quad $$ $$ \begin{array}{l} \log _a \left( {b \cdot c} \right) = \log _a \left| b \right| + \log _a \left| c \right|, \\ a > 0,\quad a \ne 1,\quad b \cdot c > 0 \\ \end{array}$$	$$\quad $$ $$ \begin{array}{l} \log _a b + \log _a c = \log _a \left( {b \cdot c} \right), \\ a > 0,\;a \ne 1,\;d > 0,\;c > 0 \\ \end{array}$$
Десятичный логарифм: $$ \lg b = \log _{10} b$$ Натуральный логарифм: $$\ln b = \log _e b$$, где $$ e = 2,71828… $$	$$\quad $$ $$ \begin{array}{l} \log _a \left( {\frac{b}{c}} \right) = \log _a \left| b \right| — \log _a \left| c \right|, \\ a > 0,\quad a \ne 1,\quad b \cdot c > 0 \\ \end{array}$$	$$\quad $$ $$ \begin{array}{l} \log _a b — \log _a c = \log _a \left( {\frac{b}{c}} \right) \\ a > 0,\;a \ne 1,\quad b > 0,\;c > 0 \\ \end{array}$$
$$\quad $$ $$ \begin{array}{l} \log _a b^n = n \cdot \log _a \left| b \right|, \\ b^n > 0,\quad n \in R \\ \end{array} $$	$$\quad $$ $$ \begin{array}{l} n \cdot \log _a b = \log _a b^n , \\ b > 0,\quad n \in R \\ \end{array}$$
Правило о знаке логарифма: $$ \log _a b $$ положителен, если основание a логарифма и число b расположены на числовой оси по одну сторону от 1, и $$ \log _a b $$отрицателен, если основание a логарифма и число b расположены на числовой оси по разные стороны от 1	$$\quad $$ $$ \begin{array}{l} \log _a b = \frac{{\log _c b}}{{\log _c a}},a > 0,a \ne 1, \\ c > 0,\quad c \ne 1,\quad b > 0 \\ \end{array}$$	$$\quad $$ $$ \begin{array}{l} \log _a b = \frac{1}{{\log _b a}},\quad a > 0,a \ne 1, \\ b > 0,\quad b \ne 1 \\ \end{array}$$
$$\quad $$ $$ \begin{array}{l} \log _{a^m } b = \frac{1}{m}\log _a b,m \in R \\ a^m > 0,\quad a^m \ne 1,\quad b > 0 \\ \end{array}$$	$$\quad $$ $$ \begin{array}{l} a^{\log _c b} = b^{\log _c a} ,a > 0,a \ne 1, \\ b > 0,\quad c > 0,\quad c \ne 1 \\ \end{array}$$

Преобразование и сравнения логарифмических выражений:

Выразить $$ \log _m n$$ через $$ a = \log _c k$$: $$ \log _m n = \frac{{\log _c n}}{{\log _c m}} = \frac{{\log _c c^z k^t }}{{\log _c c^x k^y }} = \frac{{z + t \cdot a}}{{x + y \cdot a}}$$

Сравнения:

$$ \log _a b > 0\; \Leftrightarrow \;(a > 1\; и \;b > 1)\; или \;(a < 1\; и \;b < 1)$$

$$ \log _a b < 0\; \Leftrightarrow \;(a > 1\; и \;b < 1)\; или \;(a < 1\; и \;b > 1)$$

Логарифм степени числа

Определение 2

Логарифм степени любого числа равен произведению логарифма модуля основания этой степени на показатель степени:

$\log_{a}x^r=r \cdot \log_{a}⁡|x|$

при $x^r,a > 0$, $a \ne 1$.

Пример 2

Найти значение выражения $\log_{5}⁡\frac{1}{125}+\log_{11}⁡121$.

Решение.

Представим подлогарифмические выражения в виде основания логарифма в степени и используем свойство логарифма степени:

$log_{5}\frac{1}{125}+\log_{11}⁡121=\log_{5}5^{-3}+\log_{11}11^2=-3\log_{5}⁡5+2\log_{11}⁡11=$

воспользуемся равенством $\log_{a}⁡a=1$:

$=-3+2=-1$.

Ответ: $\log_{5} \frac{1}{125}+\log_{11}⁡121=-1$.

При вычислении логарифмов справедливым является и обратное определение:

Определение 3

Коэффициент, который стоит перед логарифмом можно внести в степень подлогарифмического выражения:

$s \log_{a}⁡x=\log_{a}x^s$

при $a,b > 0$, $a \ne 1$.

Пример 3

Упростить $6 \log_{13}x^2-\log_{13}x^7$.

Решение.

Используем свойство логарифма степени и вынесем степень за знак логарифма:

$6 \log_{13}x^2-\log_{13}x^7=6 \cdot 2 \log_{13}⁡x-7 \log_{13}⁡x=12 \log_{13}⁡x-7 \log_{13}⁡x=5 \log_{13}⁡x=$

внесем коэффициент $5$ под знак логарифма:

$=\log_{13}x^5$.

Ответ: $6 \log_{13}x^2-\log_{13}x^7=\log_{13}x^5$.

Исторический очерк[]

Вещественный логарифм

Потребность в сложных расчётах в XVI веке быстро росла, и значительная часть трудностей была связана с умножением и делением многозначных чисел. В конце века нескольким математикам, почти одновременно, пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной. Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание. Первым эту идею опубликовал в своей книге «Arithmetica integra» Михаэль Штифель, который, впрочем, не приложил серьёзных усилий для реализации своей идеи.

В 1614 году шотландский математик-любитель Джон Непер опубликовал на латинском языке сочинение под названием «Описание удивительной таблицы логарифмов». В нём было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1′. Термин логарифм, предложенный Непером, утвердился в науке.

Понятия функции тогда ещё не было, и Непер определил логарифм кинематически, сопоставив равномерное и логарифмически-замедленное движение. В современной записи модель Непера можно изобразить дифференциальным уравнением: dx/x = -dy/M, где M — масштабный множитель, введенный для того, чтобы значение получилось целым числом с нужным количеством знаков (десятичные дроби тогда ещё не нашли широкого применения). Непер взял M = 10000000.

Строго говоря, Непер табулировал не ту функцию, которая сейчас называется логарифмом. Если обозначить его функцию LogNap(x), то она связана с натуральным логарифмом следующим образом:

LogNap⁡(x)=M∗(ln⁡(M)−ln⁡(x)){\displaystyle \operatorname {LogNap} (x)=M*(\ln(M)-\ln(x))}

Очевидно, LogNap(M) = 0, то есть логарифм «полного синуса» есть нуль — этого и добивался Непер своим определением. LogNap(0) = ∞.

Основное свойство логарифма Непера: если величины образуют геометрическую прогрессию, то их логарифмы образуют прогрессию арифметическую. Однако правила логарифмирования для неперовой функции отличались от правил для современного логарифма.

Например, LogNap(ab) = LogNap(a) + LogNap(b) — LogNap(1).

К сожалению, все значения таблицы Непера содержали вычислительную ошибку после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики, включая Кеплера.

В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — незаменимый инструмент инженера.

Близкое к современному понимание логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. В книге «Введение в анализ бесконечных» () Эйлер дал современные определения как показательной, так и логарифмической функций, привёл разложение их в степенные ряды, особо отметил роль натурального логарифма.

Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область.

Комплексный логарифм

Первые попытки распространить логарифмы на комплексные числа предпринимали на рубеже XVII—XVIII веков Лейбниц и Иоганн Бернулли, однако создать целостную теорию им не удалось — в первую очередь по той причине, что тогда ещё не было ясно определено само понятие логарифма. Дискуссия по этому поводу велась сначала между Лейбницем и Бернулли, а в середине XVIII века — между Даламбером и Эйлером. Бернулли и Даламбер считали, что следует определить log(-x) = log(x). Полная теория логарифмов отрицательных и комплексных чисел была опубликована Эйлером в 1747—1751 годах и по существу ничем не отличается от современной.

Хотя спор продолжался (Даламбер отстаивал свою точку зрения и подробно аргументировал её в статье своей «Энциклопедии» и в других трудах), однако точка зрения Эйлера быстро получила всеобщее признание.

Свойства логарифмов

• Вопросы занятия:
• · рассмотреть свойства логарифмов;
• ·  подробно рассмотреть примеры, в которых необходимо преобразовать выражения с логарифмами.
• Материал урока
• Прежде чем приступить к изучению новой темы, давайте повторим определение логарифма, основное логарифмическое тождество:

Эти знания нам пригодятся на сегодняшнем уроке.

Сегодня мы рассмотрим основные свойства операции логарифмирования. Заметим, что все свойства мы будем формулировать только для положительных значений переменных, содержащихся под знаком логарифма.

1. Итак, первое свойство формулируется следующей теоремой:
2. Теорема 1.
3. Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел, то есть справедлива следующая формула:

Давайте докажем эту теорему.

Введём следующие обозначения.

Нам надо доказать, что выполняется равенство:

Применим определение логарифма.

По свойству произведения степеней с одинаковыми основаниями получим:

Поскольку степени двух положительных чисел равны и основания степеней равны и отличны от единицы, то равны и показатели степеней. Значит:

Что и требовалось доказать.

Рассмотрим пример.

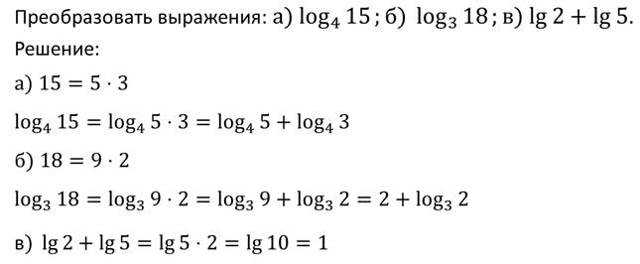
• Сформулируем следующее свойство логарифмов.
• Теорема 2.
• Если а, b, c – положительные числа, причём a ≠ 1, то справедливо равенство:

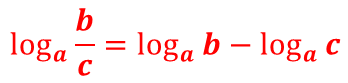
Другими словами, логарифм частного равен разности логарифмов делимого и делителя.

Или: логарифм дроби равен разности логарифмов числителя и знаменателя.

Эта теорема доказывается аналогично предыдущей. Поэтому вы можете доказать её самостоятельно, воспользовавшись свойствами степеней.

1. Рассмотрим пример.
2. Сформулируем следующее свойство.
3. Теорема 3.
4. Если а и b – положительные числа, причём, a ≠ 1, то для любого числа r справедливо равенство:
5. Другими словами, логарифм степени равен произведению показателя степени на логарифм основания степени.
6. Эта теорема доказывается аналогично предыдущим, поэтому вы можете доказать её самостоятельно, воспользовавшись свойствами степеней.
7. Рассмотрим пример.
8. Сформулируем следующее свойство.
9. Свойство.
10. Если а и b – положительные числа, причём, a ≠ 1, то для любого числа r справедливо равенство:
11. Другими словами: логарифм, основанием которого является степень числа а равен произведению единицы делённой на показатель степени и логарифма числа b по основанию а.
12. Эта теорема доказывается аналогично предыдущим, поэтому доказывать её мы не будем.
13. Рассмотрим пример.
14. Рассмотрим ещё один пример.

То есть нам удалось логарифм достаточно громоздкого выражения представить в виде суммы и разности логарифмов простых выражений. Такое преобразование называют логарифмированием.

Иногда приходиться решать обратную задачу: находить выражение, логарифм которого представлен через логарифмы некоторых чисел. Такое действие называется потенцированием.

При этом используют следующее утверждение:

• Теорема 4.
• Равенство:
• справедливо тогда и только тогда, когда
• Это утверждение следует из монотонности логарифмической функции.
• Рассмотрим пример.

Ещё раз обратите внимание, что все свойства логарифмов мы получили при условии, что переменные принимают положительные значения. А как быть, если про знак переменной ничего неизвестно?

1. Например, можно ли записать:
2. Нет, нельзя, поскольку:
3. Правильнее будет записать так:
4. Мы должны помнить и о том, что:
5. только в том случае, когда b > 0 и с > 0. Если мы в этом не уверены, но знаем, что произведение bc > 0, то, поскольку в этом случае выполняется равенство:
6. то следует использовать формулу:
7. Рассмотрим ещё несколько примеров.
8. Пример.
9. Пример.
10. Пример.
11. Пример.
12. Итак, повторим основные свойства логарифмов:

Использование свойств логарифмов при решении логарифмических уравнений и неравенств

Чтобы не делать ошибок при решении логарифмических уравнений и неравенств, следует внимательно и аккуратно пользоваться свойствами логарифмов, перечисленными в предыдущем разделе.

Например, если вам нужно преобразовать выражение при решении уравнения или неравенства

лога (f(x)2) ,

тогда вместо формулы

необходимо использовать формулу

потому что иначе можно потерять корни.

По той же причине при преобразовании выражений

loga(f(x)g(x)) и

следует использовать формулы:

Комментарий. Тем, кто хочет усовершенствовать свои знания и навыки решения уравнений и неравенств с логарифмами, рекомендуем ознакомиться с нашими учебниками «Решение логарифмических уравнений» и «Решение логарифмических неравенств».

ОДЗ в логарифмических неравенствах. Как сделать проще?

Иногда можно немного упростить себе жизнь при поиске ОДЗ в неравенствах. Для этого нам понадобится немного логики. Разберем на примере:

Пример 7
$$1+\log_{6}(4-x)\leq\log_{6}(16-x^2).$$
Выпишем ОДЗ, но не будем его решать — да, так можно делать!

ОДЗ выписали, теперь преобразуем исходное неравенство. Для этого \(1\) представим в виде логарифма с основанием \(6\): \(1=\log_{6}(6)\). И воспользуемся формулой:
$${ \small \log_{a}(bc)=\log_{a}(b)+\log_{a}(c);}$$
$${ \small \log_{6}(6)+\log_{6}(4-x)\leq\log_{6}(16-x^2);}$$
$${ \small \log_{6}(6*(4-x))\leq\log_{6}(16-x^2);}$$
Сравниваются два логарифма с одинаковым основанием, можем смело избавляться от логарифмов, сохраняя знак неравенства:
$$6*(4-x)\leq16-x^2;$$

И вот здесь остановимся и поговорим

Согласно ОДЗ
$$\begin{cases}
4-x>0, \\
16-x^2>0.
\end{cases}$$
Обратите внимание! Что, если: \(6*(4-x)\geq0\), то и \(16-x^2\) будет больше \(0\) автоматически, так как мы решаем неравенство:
$$6*(4-x)\leq16-x^2;$$
$$0 \leq 6*(4-x)\leq16-x^2;$$. Что избавляет нас от необходимости решать \(16-x^2>0\), это будет лишним действием

Конкретно в этом примере нет большой трудности решить все условия из ОДЗ и не думать. Но часто встречаются примеры, в которых выше представленная логика поможет вам не запутаться, ведь иногда это спасает от необходимости решения очень сложных неравенств. Особенно это касается решения заданий с параметрами в профильном ЕГЭ по математике. Вот там каждое лишнее условие в разы увеличивает объем работы

Что избавляет нас от необходимости решать \(16-x^2>0\), это будет лишним действием.
Конкретно в этом примере нет большой трудности решить все условия из ОДЗ и не думать. Но часто встречаются примеры, в которых выше представленная логика поможет вам не запутаться, ведь иногда это спасает от необходимости решения очень сложных неравенств. Особенно это касается решения заданий с параметрами в профильном ЕГЭ по математике. Вот там каждое лишнее условие в разы увеличивает объем работы.

Дорешаем пример:
$$ \begin{cases}
6*(4-x)\leq16-x^2, \\
6*(4-x)>0.
\end{cases}$$

$$ \begin{cases}
24-6x\leq16-x^2, \\
4-x>0.
\end{cases}$$

$$ \begin{cases}
x^2-6x+8\leq0, \\
x>4.
\end{cases}$$

$$ \begin{cases}
2 \leq x \leq 4, \\
4-x>0.
\end{cases}$$
Ответ: \(x \in [2;4).\)

Логарифмические таблицы[]

Логарифмические таблицы

Из свойств логарифма следует, что вместо трудоёмкого умножения многозначных чисел достаточно найти (по таблицам) и сложить их логарифмы, а потом по тем же таблицам выполнить потенцирование, то есть найти значение результата по его логарифму. Выполнение деления отличается только тем, что логарифмы вычитаются. Лаплас говорил, что изобретение логарифмов «продлило жизнь астрономов», многократно ускорив процесс вычислений.

При переносе десятичной запятой в числе на n{\displaystyle n} разрядов значение десятичного логарифма этого числа изменяется на n{\displaystyle n}. Например, lg⁡8314,63=lg⁡8,31463+3{\displaystyle \lg 8314{,}63=\lg 8{,}31463+3}. Отсюда следует, что достаточно составить таблицу десятичных логарифмов для чисел в диапазоне от 1 до 10.

Первые таблицы логарифмов опубликовал Джон Непер (), и они содержали только логарифмы тригонометрических функций, причём с ошибками. Независимо от него свои таблицы опубликовал Иост Бюрги, друг Кеплера (). В 1617 году оксфордский профессор математики Генри Бригс опубликовал таблицы, которые уже включали десятичные логарифмы самих чисел, от 1 до 1000, с 8 (позже — с 14) знаками. Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Вега () появилось только в 1857 году в Берлине (таблицы Бремивера).

В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого. В СССР выпускались несколько сборников таблиц логарифмов.

Брадис В. М. Четырехзначные математические таблицы. 44-е издание, М., 1973.

Таблицы Брадиса () использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.

Вега Г. Таблицы семизначных логарифмов, 4-е издание, М., 1971.

Профессиональный сборник для точных вычислений.

• Пятизначные таблицы натуральных значений тригонометрических величин, их логарифмов и логарифмов чисел, 6 изд., М.: Наука, 1972.
• Таблицы натуральных логарифмов, 2-е издание, в 2 томах, М.: Наука, 1971.