Периметр равностороннего треугольника — формула и примеры нахождения

Примеры задач

Задание 1
Вычислите длину медианы равностороннего треугольника, если известно, что его сторона равна 6 см.

Решение
Чтобы найти требуемое значение, примените приведенную выше формулу:

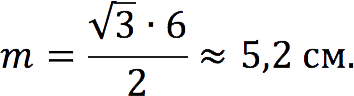
Задача 2
Наибольшая сторона одного из треугольников, образованных в результате пересечения трех медиан в равностороннем треугольнике, равна 8 см. Найдите длину стороны этого треугольника.

Решение
Нарисуем дрежей сообщение сообщение отзывым такаи.

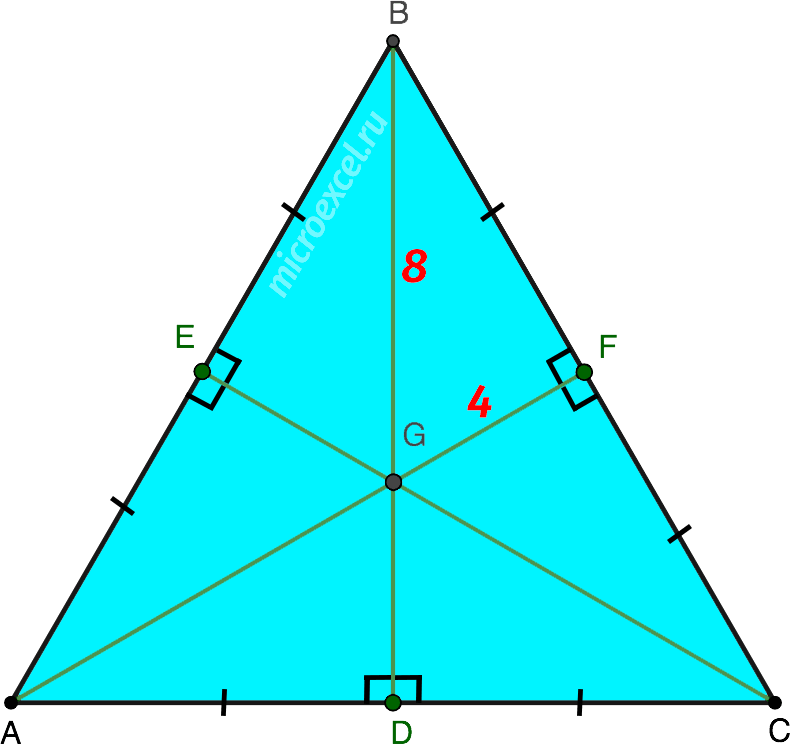
Из свойства 5 мы знаем, что в результате пересечения всех медиан образуется 6 прямоугольных треугольников.

• BG = 8 см (самая большая строна, на языке гипотенузой △BFG);
• FG = 4 см (катет △BFG, в 2 раза менеше гипотенузы BG – след из Свойства 3).

Применим теорему Пифагора, чтобы найти длину второй ноги BF:
BF2 = BG2 – FG2 = 82 – 42 = 48 см2.
Следовательно, BF ≈ 6,93 см.

BF соответствует полове смотров BC (т.к медиана делит строней треугольника пополам), следовательно, BC ≈ 13,86 см.

Решение задачи

Для закрепления теоретического материала преподаватель учащимся предлагает решить ряд задач. Самостоятельное вычисление ответа позволяет не только научиться применять знания на практике, но и разобраться в различных тонкостях. Вот одна из таких задач, рассчитанная на школьников среднего уровня подготовки.

Дан равносторонний треугольник ABC. Длина медианы BH, проведённой на основание AC, составляет 9 * √3. Определить, чему равны стороны фигуры

Перед тем как непосредственно перейти к решению, нужно обратить внимание, что все стороны у фигуры будут одинаковые, при этом углы также равны. По сути, равносторонний многоугольник является равнобедренным, поэтому медиана является и высотой, а значит, угол H будет составлять 90 градусов

При этом все остальные углы равны 60 градусам.

Решить задачу можно двумя способами:

1. Первый предполагает решение через тригонометрические функции. Так как известен острый угол в прямоугольном треугольнике ABH, используя синус (значение противолежащего катета к гипотенузе) можно записать: sin BAH = BH / AB. Отсюда AB = BH / sin BAH = (9 * √3) / (√3 / 2) = 9 * 2 = 18.
2. В основе второго способа лежит теорема Пифагора. Сторона AB — это гипотенуза. Для удобства её можно обозначить как х. Так как медиана делит сторону пополам, то AH = x / 2. По теореме: AB2 = AH2 + BH2. Подставив известные значения в формулу, можно получить выражение: x2 = (x/2) 2 + (9 * √3) 2 = (x 2 / 4) + 81 * 3 = 81 * 4. Отсюда x = √ 81 * √ 4 = 9 * 2 = 18.

Следует отметить, что формула: m = a √3 / 2 называется выражением медианы через высоту. И находится она как раз по теореме Пифагора. Это позволяет, зная лишь высоту или биссектрису, находить не только величину сторон, но и площадь фигуры, радиусы вписанной и описанной окружностей. При этом эта формула работает и в обратном направлении. Так, сторона будет равна: а = m / (√3 / 2).

Теорема о медиане и площади треугольника

Почему? А давай вспомним самую простую форму площади треугольника. \( S=\frac{1}{2}a~\cdot h\).

И применим эту формулу аж два раза!

Посмотри, медиана \( \displaystyle BM\) разделила \( \displaystyle \triangle ABC\) на два треугольника: \( \displaystyle \triangle ABM\) и \( \displaystyle \triangle BMC\).

Но! Высота-то у них одна и та же – \( \displaystyle BH\)!

Только в \( \displaystyle \triangle ABM\) эта высота \( \displaystyle BH\) опускается на сторону \( \displaystyle AM\), а в \( \displaystyle \triangle BMC\) – на продолжение стороны \( \displaystyle CM\).

Удивительно, но вот бывает и так: треугольники разные, а высота – одна. И вот, теперь-то и применим два раза формулу

\( S=\frac{1}{2}a~\cdot h\).

1) B \( \displaystyle \triangle ABM\):

«\( \displaystyle a\)» – это \( \displaystyle AM\)«\( \displaystyle h\)» – это \( \displaystyle BH\)

\( \displaystyle \Rightarrow {{S}_{\triangle ABM}}=\frac{1}{2}~AM~\cdot BH\)

2) B \( \displaystyle \triangle BMC\):

«\( \displaystyle a\)» – это \( \displaystyle CM\)«\( \displaystyle h\)» – это опять \( \displaystyle BH\)

\( \displaystyle \Rightarrow {{S}_{\triangle BMC}}=\frac{1}{2}~CM~\cdot BH\)

Теорема о периметре

Каждому ученику известна формула периметра треугольника для 3 класса. Она является довольно примитивным соотношением, и применяется в абсолютно другом виде в старших классах и высших учебных заведениях. Математики предлагают рассмотреть доказательство теоремы о периметре правильного треугольника. Ее формулировка имеет следующий вид: периметр треугольника равен утроенному произведению одной из его сторон, когда фигура является правильной.

Доказывается утверждение очень просто. Для этого необходимо использовать следующий алгоритм:

1. Обозначить стороны треугольника литерами «m», «n» и «о».
2. Записать формулу периметра P в общем виде: P=m+n+o.
3. Используя определение и свойство сторон правильного треугольника, записать соотношение во втором пункте с условием равенства всех сторон величине q в виде следующей формулы: P=q+q+q=3q.
4. На основании соотношения, полученного в третьем пункте алгоритма, теорема доказана полностью.

Можно найти и другое доказательство теоремы, в которой используется прямоугольник. В фигуре нужно провести диагонали, а затем по формуле Пифагора выразить боковые стороны. Однако процесс доказательства утверждения является более сложным.

Общие сведения

Изучение любой фигуры, процесса или явления всегда начинается с определений. Треугольником называется геометрическое тело, состоящее из трех, не лежащих на одной прямой, вершин. Прямая — совокупность бесконечного количества точек, лежащих в одной плоскости и проходящих без искажений.

Вершина — точка, образованная сторонами треугольника. Периметр — суммарное значение всех сторон любой фигуры. Высота — отрезок, проведенный из любой вершины на сторону, которая является противоположной, под углом в 90 градусов.

Медиана — часть прямой, проведенной из вершины, но не под прямым углом, а соединяющая ее с серединой противолежащей стороны. Биссектриса — прямая, делящая угол на 2 равных величины.

Необходимые данные

Для вывода формул потребуется вспомнить несколько теоретических выкладок:

• Медиана это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Три медианы треугольника пересекаются в одной точке.
• В равнобедренном треугольнике, медиана, проведенная к основанию, является биссектрисой и высотой. А правильный треугольник это частный случай равнобедренного треугольника, у которого основанием может выступать любая из сторон. Значит каждая медиана равностороннего треугольника будет совпадать с соответствующей биссектрисой и высотой.
• В правильном треугольнике все стороны равны, а каждый из углов равен 60 градусам.

Задачи с разными видами треугольников

№1. Дан равнобедренный треугольник. Его периметр известен и равен 90 см. Требуется узнать его стороны. В качестве дополнительного условия: боковая сторона меньше основания в 1,2 раза.

Решение

Значение периметра напрямую зависит от тех величин, которые нужно найти. Сумма всех трех сторон и даст 90 см. Теперь нужно вспомнить признак треугольника, по которому он является равнобедренным. То есть две стороны равны. Можно составить уравнение с двумя неизвестными: 2а + в = 90. Здесь а — боковая сторона, в — основание.

Настала очередь дополнительного условия. Следуя ему, получается второе уравнение: в = 1,2а. Можно выполнить подстановку этого выражения в первое. Получится: 2а + 1,2а = 90. После преобразований: 3,2а = 90. Отсюда а = 28,125 (см). Теперь несложно узнать основание. Лучше всего это сделать из второго условия: в = 1,2 * 28,125 = 33,75 (см).

Для проверки можно сложить три значения: 28,125 * 2 + 33,75 = 90 (см). Все верно.

Ответ: стороны треугольника равны 28,125 см, 28,125 см, 33,75 см.

№2. Сторона равностороннего треугольника равна 12 см. Нужно вычислить его высоту.

Решение. Для поиска ответа достаточно вернуться к тому моменту, где были описаны свойства треугольника. Так указана формула для нахождения высоты, медианы и биссектрисы равностороннего треугольника.

н = а * √3 / 2, где н — высота, а — сторона.

Подстановка и вычисление дают такой результат: н = 6 √3 (см).

Эту формулу необязательно запоминать. Достаточно вспомнить, что высота делит треугольник на два прямоугольных. Причем она оказывается катетом, а гипотенуза в нем — это сторона исходного, второй катет — половина известной стороны. Теперь нужно записать теорему Пифагора и вывести формулу для высоты.

Ответ: высота равна 6 √3 см.

№3. Дан МКР — треугольник, 90 градусов в котором составляет угол К. Известны стороны МР и КР, они равны соответственно 30 и 15 см. Нужно узнать значение угла Р.

Решение. Если сделать чертеж, то становится ясно, что МР — гипотенуза. Причем она в два раза больше катета КР. Снова нужно обратиться к свойствам. Одно из них как раз связано с углами. Из него понятно, что угол КМР равен 30º. Значит искомый угол Р будет равен 60º. Это следует из другого свойства, которое утверждает, что сумма двух острых углов должна равняться 90º.

Ответ: угол Р равен 60º.

№4. Нужно найти все углы равнобедренного треугольника. Про него известно, что внешний угол от угла при основании равен 110º.

Решение. Поскольку дан только внешний угол, то этим и нужно воспользоваться. Он образует с внутренним углом развернутый. Значит в сумме они дадут 180º. То есть угол при основании треугольника будет равен 70º. Так как он равнобедренный, то второй угол имеет такое же значение. Осталось вычислить третий угол. По свойству, общему для всех треугольников, сумма углов равна 180º. Значит, третий определится как 180º – 70º – 70º = 40º.

Ответ: углы равны 70º, 70º, 40º.

№5. Известно, что в равнобедренном треугольнике угол, лежащий напротив основания, равен 90º. На основании отмечена точка. Отрезок, соединяющий ее с прямым углом, делит его в отношении 1 к 4. Нужно узнать все углы меньшего треугольника.

Решение. Один из углов можно определить сразу. Поскольку треугольник прямоугольный и равнобедренный, то те, что лежат у его основания, будут по 45º, то есть по 90º/2.

Второй из них поможет найти известное в условии отношение. Поскольку оно равно 1 к 4, то частей, на которые он делится получается всего 5. Значит, чтобы узнать меньший угол треугольника нужно 90º/5 = 18º. Осталось узнать третий. Для этого из 180º (суммы всех углов треугольника) нужно вычесть 45º и 18º. Вычисления несложные, и получится: 117º.

Ответ: 18º, 45º, 117º

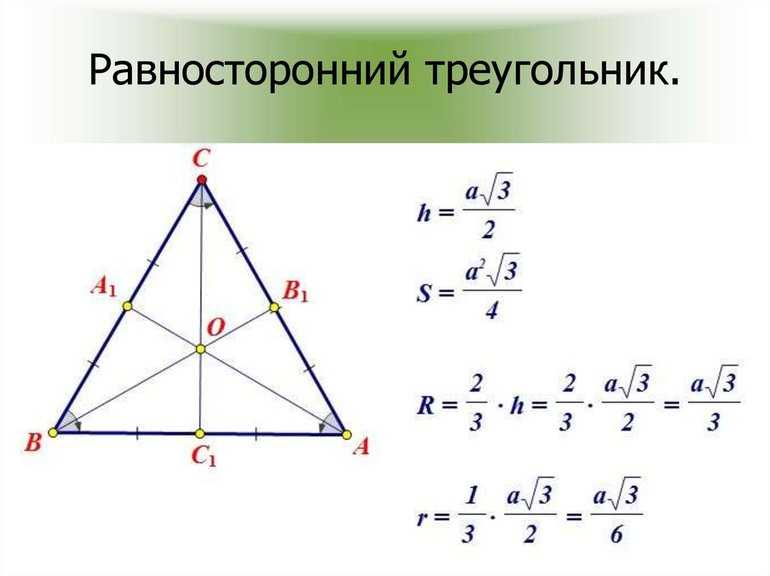
Медиана равностороннего треугольника

Какими свойствами обладает медиана равностороннего треугольника? Как выразить длину медианы через сторону треугольника? Через радиус вписанной и описанной окружностей?

(свойство медианы равностороннего треугольника)

В равностороннем треугольнике медиана, проведённая к любой стороне, является также его биссектрисой и высотой.

Проведём медиану BF.

Так как AB=BC, треугольник ABC — равнобедренный с основанием AC.

По свойству медианы равнобедренного треугольника, BF является также его биссектрисой и высотой.

так как AC=BC, треугольник ABC — равнобедренный с основанием AB, CD — его медиана, биссектриса и высота.

Что и требовалось доказать .

(свойство медиан равностороннего треугольника)

Все три медианы равностороннего треугольника равны между собой.

AK, BF, CD — его медианы.

Следовательно, треугольники ABK, BCF и CAK равны (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих сторон:

Что и требовалось доказать .

Из 1 и 2 теоремы следует, что все медианы, биссектрисы и высоты равностороннего треугольника равны между собой.

1) Выразим длину медианы равностороннего треугольника через его сторону.

Обозначим AB=a, BF=m, тогда AF=a/2.

Таким образом, формула медианы равностороннего треугольника по его стороне:

2) Выразим медиану равностороннего треугольника через радиусы вписанной и описанной окружностей.

Центр правильного треугольника является центром его вписанной и описанной окружностей.

Так как медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то BO:OF=2:1. Таким образом,

Отсюда медиана равностороннего треугольника через радиус вписанной окружности равна

Длина высоты и ее частей

Прежде чем приводить формулы площади равностороннего треугольника, следует выяснить, какую длину имеют его биссектрисы, высоты или медианы. Пусть эта величина будет обозначаться латинской буквой h, а сторона фигуры обозначается a. Поскольку проведенная высота из любого угла делит его на 2 прямоугольных треугольника, этот факт можно использовать для вычисления величины h. Проще всего применить определение какой-либо тригонометрической функции, например, синуса:

sin (60) = h/a.

Согласно определению, синусом угла называется отношения противолежащего катета (h) к гипотенузе (a). Поскольку значения функции sin (60) является табличной величиной, получается следующее выражение для h:

h = 30,5 /2*a.

Для получения полной информации о свойствах биссектрис, медиан и высот треугольника, нужно определить, на какие части делит их точка пересечения. Следует ввести некоторые обозначения:

• A, B, C — вершины равноугольного треугольника;
• Q — точка пересечения биссектрис, медиан и высот фигуры;
• P — середины стороны BC, на которую опущена высота AP.

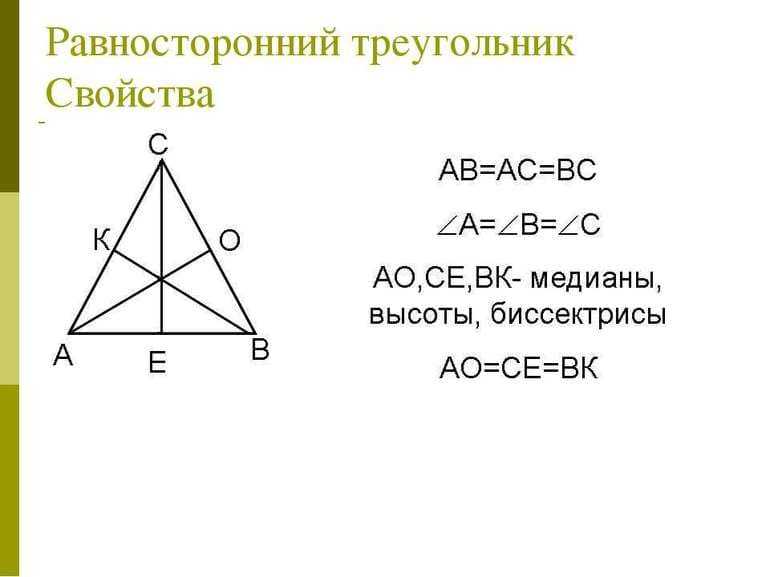
Треугольник PQB является прямоугольным. Прямым углом будет QPB. Поскольку угол QBP разделен биссектрисой на 2 одинаковые части, он составляет 30 градусов. Катет QP лежит против этого угла, поэтому будет иметь длину в 2 раза меньшую, чем гипотенуза BQ. Нетрудно увидеть, что сумма длин BQ и QP равна высоте h. Эти рассуждения позволяют получить следующие формулы:

• QP = ½*BQ = 1/3*h = 30,5 /6*a = r;
• BQ = 2*QP = 2/3*h = 30,5 /3*a = R.

Примеры задач

Задача 1 Вычислите длину медианы равностороннего треугольника, если известно, что его сторона равна 6 см.

Решение Для нахождения требуемого значения применим формулу выше:

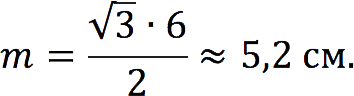
Задача 2 Самая большая сторона одного из треугольников, образованных в результате пересечения трех медиан в равностороннем треугольнике, равняется 8 см. Найдите длину стороны данного треугольника.

Решение Нарисуем чертеж согласно условиям задачи.

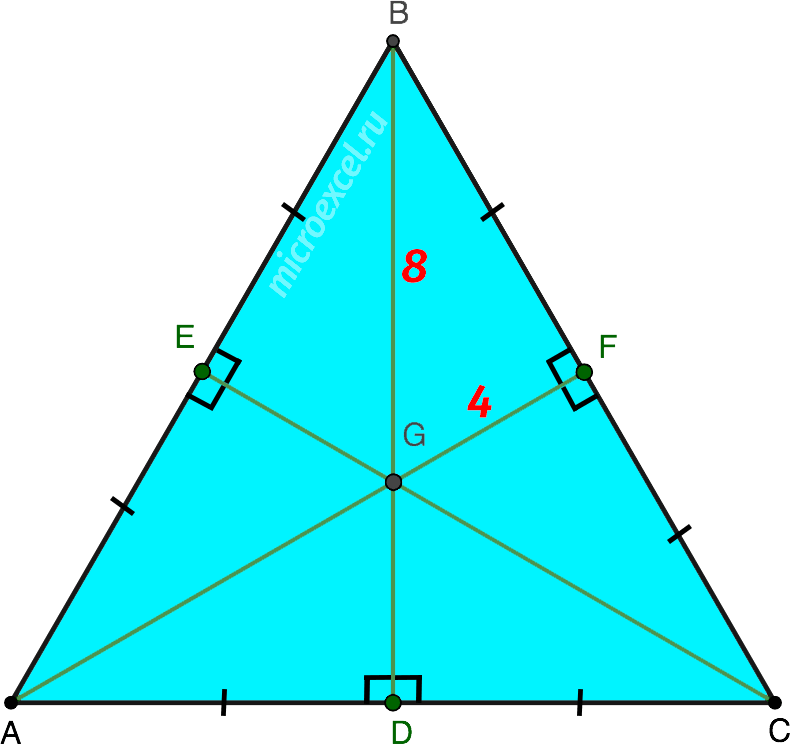
Из Свойства 5 мы знаем, что в результате пересечения всех медиан образуются 6 прямоугольных треугольников.

• BG = 8 см (самая большая сторона, является гипотенузой △BFG);
• FG = 4 см (катет △BFG, в 2 раза меньше гипотенузы BG – следует из Свойства 3).

Применяем теорему Пифагора, чтобы найти длину второго катета BF:BF 2 = BG 2 – FG 2 = 8 2 – 4 2 = 48 см 2 . Следовательно, BF ≈ 6,93 см.

BF равняется половине стороны BC (т.к. медиана делит сторону треугольника пополам), следовательно, BC ≈ 13,86 см.

Пример задачи

Свойство 3. В равностороннем треугольнике радиус перикруга в два раза больше радиуса конечного круга. \(R=2\cdot r\)

Теперь должно быть понятно, почему это так.

Публикации по теме:

• Нахождение площади квадрата: формула и примеры
• Нахождение площади прямоугольника: формула и пример
• Нахождение площади треугольника: формула и примеры
• Нахождение площади круга: формула и примеры
• Нахождение площади ромба: формула и примеры
• Нахождение площади трапеции: формула и примеры
• Нахождение площади параллелограмма: формула и примеры
• Нахождение площади эллипса: формула и пример
• Нахождение площади выпуклого четырехугольника: формула и пример
• Нахождение периметра квадрата: формула и задачи
• Нахождение периметра прямоугольника: формула и задачи
• Нахождение периметра ромба: формула и задачи
• Нахождение периметра трапеции: формула и задачи
• Нахождение периметра параллелограмма: формула и задачи
• Нахождение длины окружности: формула и задачи
• Теорема Пифагора для прямоугольного треугольника: формула и задачи
• Теорема косинусов для треугольника: формула и задачи
• Теорема о сумме углов треугольника: формула и задачи
• Тригонометрические функции острого угла в прямоугольном треугольнике
• Нахождение объема конуса: формула и задачи
• Нахождение объема куба: формула и задачи
• Нахождение объема шара: формула и задачи
• Нахождение объема пирамиды: формула и задачи
• Нахождение площади правильного шестиугольника: формула и примеры
• Нахождение объема тетраэдра: формула и задачи
• Нахождение объема призмы: формула и задачи
• Нахождение площади поверхности куба: формула и задачи
• Нахождение площади поверхности цилиндра: формула и задачи
• Нахождение площади поверхности конуса: формула и задачи
• Нахождение площади поверхности шара (сферы): формула и задачи
• Нахождение площади поверхности вписанного в цилиндр шара
• Нахождение радиуса шара: формула и примеры
• Нахождение радиуса круга: формула и примеры
• Нахождение радиуса цилиндра: формула и примеры
• Нахождение площади правильной призмы: формула и задачи
• Нахождение площади правильной пирамиды: формулы
• Формула Герона для треугольника
• Теорема Менелая: формулировка и пример с решением
• Теорема о внешнем угле треугольника: формулировка и задачи
• Теорема Чевы: формулировка и пример с решением
• Теорема Стюарта: формулировка и пример с решением
• Теорема о трех перпендикулярах
• Теорема Фалеса: формулировка и пример решения задачи
• Геометрическая фигура: треугольник
• Признаки равенства треугольников
• Признаки подобия треугольников
• Признаки равенства прямоугольных треугольников
• Свойства равнобедренного треугольника: теория и задача
• Определение и свойства медианы треугольника
• Определение и свойства медианы прямоугольного треугольника

Медиана в равностороннем треугольнике свойства

Формулы. N = 2i. N — мощность алфавита (количество знаков в алфавите) i — информационный вес символа алфавита (количество информации в одном символе). I = K * i. I — количество информации, содержащееся в выбранном сообщении (информационный объем сообщения) K — число символов в.

Какие из данных утверждений верны? Запишите их номера. 1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны. 2) Диагональ трапеции делит её на два равных треугольника. 3) Если в ромбе один из углов равен 90° , то такой ромб — квадрат.

Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются Вершинами треугольника, а отрезки — его Сторонами.

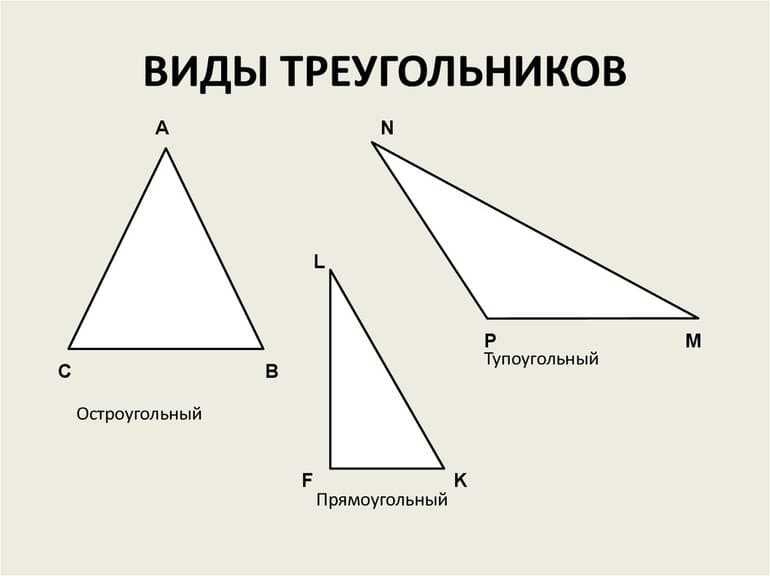
Виды треугольников

Треугольник называется Равнобедренным, если у него две сторны равны. Эти равные стороны называются Боковыми сторонами, а третья сторона называется Основанием треугольника.

Треугольник, у которого все сторны равны, называется Равносторонним или Правильным.

Треугольник называется Прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому углу, называется Гипотенузой, две другие стороны называются Катетами.

Треугольник называется Остроугольным, если все три его угла — острые, то есть меньше 90°.

Треугольник называется Тупоугольным, если один из его углов — тупой, то есть больше 90°.

Основные линии треугольника

Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.

Свойства медиан треугольника

Центром тяжести

Биссектриса

Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.

Свойства биссектрис треугольника

Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла. Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилегажащим сторонам: . Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.

Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.

Свойства высот треугольника

В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному. В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.

Срединный перпендикуляр

Прямую, проходящую через середину отрезка перпендикулярно к нему, называют Серединным перпендикуляром к отрезку.

Свойства серединных перпендикуляров треугольника

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему. Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.

Признаки равенства треугольников

Два треугольника равны, если у них соответственно равны:

две стороны и угол между ними; два угла и прилежащая к ним сторона; три стороны.

Подобие треугольников

Два треугольника Подобны, если выполняется одно из следующих условий, называемых Признаками подобия:

два угла одного треугольника равны двум углам другого треугольника; две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами, равны; три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника.

В подобных треугольниках соответствующие линии (высоты, медианы, биссектрисы и т. п.) пропорциональны.

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов, причем коэффициент пропорциональности равен диаметру описанной около треугольника окружности:

Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

A 2 = B 2 + C 2 — 2Bc cos

Треугольник с равными сторонами

Каждый школьник, в каком бы классе он ни учился, знает, что собой представляет треугольник. Он является самой простой замкнутой фигурой на плоскости и в пространстве, поскольку образован тремя отрезками (четырьмя ограничены следующие по сложности за ним фигуры: прямоугольник, квадрат, параллелограмм и т. д. ).

Состоит он из трех сторон, которые определяют 3 его угла (отсюда и название геометрического объекта). Для определения значений углов в градусах следует при решении задач использовать теорему о равенстве их суммы — 180

При этом неважно, к какому типу относится сама фигура (равнобедренный, прямоугольный и т. д

), теорема остается справедливой всегда.

Исходя из названия, равносторонний треугольник — плоская фигура, все 3 стороны которой равны между собой. Для нее являются справедливыми следующие свойства:

• Все 3 угла равны между собой и составляют 60 градусов, поэтому его также называют равноугольным. Это утверждение справедливо в обратную сторону: если все углы треугольника составляют 60 градусов, он является равносторонним.
• Медиана, биссектриса и высота совпадают друг с другом, то есть любая из этих линий будет делить угол пополам, противоположную сторону на 2 равные части и будет перпендикулярна ей одновременно.
• Наличие трех осей симметрии. Все они совпадают с соответствующими медианами, биссектрисами, высотами. Оси пересекаются в точке, которая является геометрическим и массовым центром фигуры. Повороты на 0, 120, 240 и 360 градусов вокруг этой точки треугольника будут переводить его самого в себя, то есть являются операциями симметрии.
• Любые 2 рассматриваемых треугольника являются подобными. Этот вывод следует из равенства их трех углов.

Формулы площади

Чему равна площадь равностороннего треугольника можно определить с использованием нескольких формул. Для этого привлекаются в том числе понятия вписанной и описанной окружности.

Через величины a или h

Площадь абсолютно любого треугольника может быть определена как произведение его высоты на длину основания, которое следует поделить пополам. Если записать это выражение для равноугольного треугольника, можно получить следующие формулы:

• S = ½*a*h;
• S = 30,5 /4*a 2 ;
• S = 30,5 /3*h 2 .

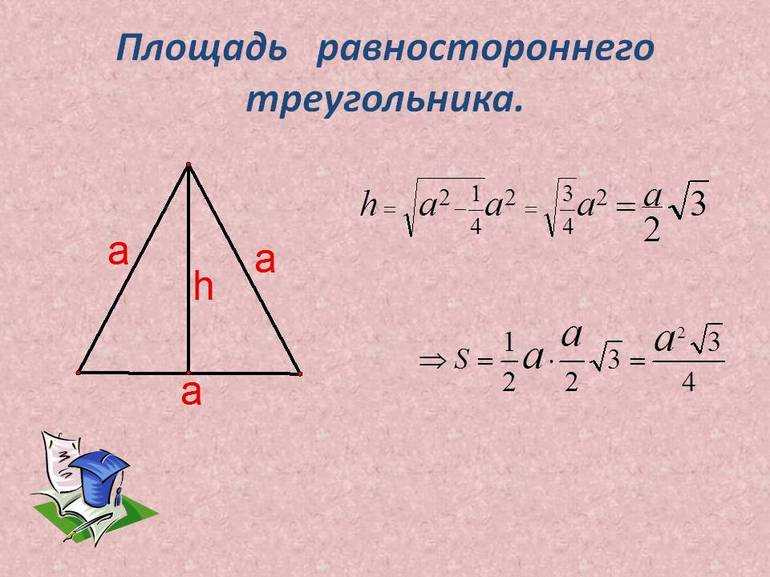
Для получения этих выражений была использована формула связи между длинами высоты h и основания a. Уравнения справедливы для любого треугольника с равными сторонами. Для прямоугольного или равнобедренного эти выражения уже не подходят.

Через радиусы r или R

Чтобы определить площадь, достаточно узнать любой линейный параметр. Это необязательно может быть сторона или высота, но также радиусы вписанной и описанной окружностей.

Вписанной называется окружность, которая лежит внутри фигуры и касается всех ее сторон. В случае равностороннего треугольника ее центр находится в точке пересечения медиан (высот, биссектрис), то есть в точке Q. Ее радиус r равен отрезку QP и составляет:

r = 30,5 /6*a.

Выразив из этого равенства сторону a и подставив ее в формулу для площади S через a, можно получить следующее выражение:

S = 3*30,5 *r 2 .

Центр вписанной окружности является для равностороннего треугольника центром описанной вокруг него. Ею принято называть в геометрии фигуру, которая проходит через все вершины многоугольника. Поскольку ее центр лежит в точке Q, радиус R будет равен длине отрезка QB. Формула для него уже известна:

R = 30,5 /3*a.

Аналогичным образом, выражая из этого равенства величину a, и подставляя ее в формулу для S, можно получить следующее выражение:

S = 3*30,5/4*R 2 .

Это равенство можно было также получить, если вспомнить, что радиус описанной окружности R в 2 раза больше радиуса r.

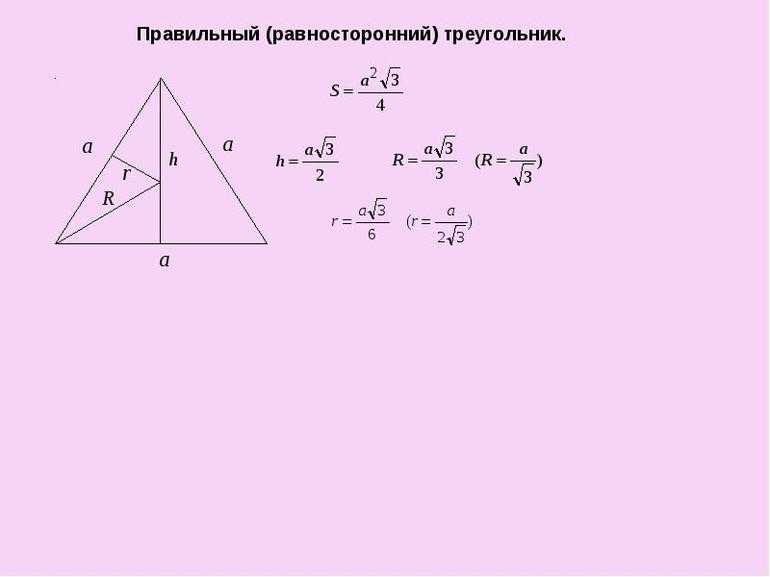
Определение правильного треугольника

Треугольник называется правильным, если все его стороны равны: AB + AC + BC. Правильный треугольник еще называется равносторонним.

Общие сведения

Любое пространство можно описать размерностью. В трёхмерном измерении плоская геометрическая фигура, состоящая из трёх отрезков и такого же количества точек, в которых они соединяются, называется треугольником. Отрезки называют сторонами или боковыми гранями, площадь, ограниченная ими — внутренней, а точки — вершинами. Фигура имеет 3 угла и является невырожденной.

Строгого требования к обозначениям элементов многоугольника нет. Но традиционно вершины подписывают заглавными буквами латинского алфавита A, B, C, а противолежащие им стороны — аналогичными строчными знаками. В качестве обозначений для углов используют греческие символы: α, β, γ. Например, если имеется треугольник ABC, у него будут углы A, B, C и стороны a, b, c. Боковые грани могут подписываться и как отрезки, тогда в их имени учитываются ограничивающие точки. Например, AB, BC, CA.

В зависимости от соотношения размеров сторон, все треугольники разделяют на 3 вида. Они бывают:

• Равнобедренными — многоугольники, у которых одна сторона не равна двум другим. Эта грань называется основанием. Углы при этой стороне равны.
• Разносторонние (неправильные) — длины всех граней разные.
• Равносторонние — треугольники, имеющие одинаковые стороны. Часто эти фигуры называют правильными. По сути, они являются частным случаем равнобедренного многоугольника.

Существуют правила, позволяющие утверждать о равенстве или подобии двух и более треугольников. Они считаются идентичными, то есть их параметры полностью совпадают, если 2 стороны и угол равны или все грани имеют одинаковую длину. А также фигуры будут одинаковыми, когда у них совпадают 2 стороны и угол, располагающийся напротив большего отрезка.

Особые линии и точки

Медиана, высота и биссектриса — 3 замечательные линии любого треугольника. Представляют они собой внутренние отрезки, построенные из углов на противоположные стороны. Линия, соединяющая вершину с серединой противоположной грани, называется медианой. Луч, разделяющий угол на 2 равные части — это биссектриса, а перпендикуляр, построенный к стороне — высота.

В любом правильном треугольнике можно начертить 3 отрезка. Если отложить медиану, а потом биссектрису и высоту, можно заметить, что эти линии совпадут. Эта особенность и есть замечательным свойством равностороннего многоугольника, то есть если в любой другой трёхугольной фигуре можно построить 12 особых линий, то в рассматриваемом только 3.

Доказать это утверждение можно следующим образом: пусть имеется треугольник АВС, в котором проведена высота ВH. Далее, рассуждения нужно построить так:

• Отрезок BH перпендикулярен прямой AC по построению.
• Точка H разделяет отрезок AC на AD и CD. Если это утверждение будет верным, это означает, что построенная высота BH будет медианой треугольника.
• Отрезок BH создаёт в многоугольнике 2 угла — ∠ABH и ∠CBH. При верности этого утверждения можно утверждать, что отрезок BH является биссектрисой.

Если создать зеркальное отражение треугольнику и совместить его с оригинальным, все углы попарно совместятся. Совпадут и стороны. Так как ВH — высота, она перпендикуляр. Значит, в точке H отрезок образует прямой угол с боковой гранью AC. Отсюда следует, что образованные треугольники AHB и CBH прямоугольные.

Они являются равными по общей гипотенузе и острому углу. Это следует из того, что правильный многоугольник — частный случай равнобедренного. Так как треугольники совпадают, у них одинаковые углы ABH и CBH. Причём они смежные, поэтому BH — биссектриса. В то же время точка H делит AC на 2 равных отрезка, значит, BH — медиана.

Медиана равностороннего треугольника

Средняя оценка: 4.6

Всего получено оценок: 93.

Средняя оценка: 4.6

Всего получено оценок: 93.

Равносторонний треугольник стоит особняком среди всех фигур: в нем легко можно найти значение всех сторон и углов, так как все углы известны заранее, а найдя одну сторону, можно найти сразу все три. Но именно из-за этих свойств, составители задач любят писать каверзные условия, в которых не всегда можно разобраться с первого раза, например, не всегда можно понять, что такое медиана, потому что человеку проще воспринимать понятие высоты, нежели медианы. Рассмотрим же понятие медианы в равностороннем треугольнике подробно.