Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
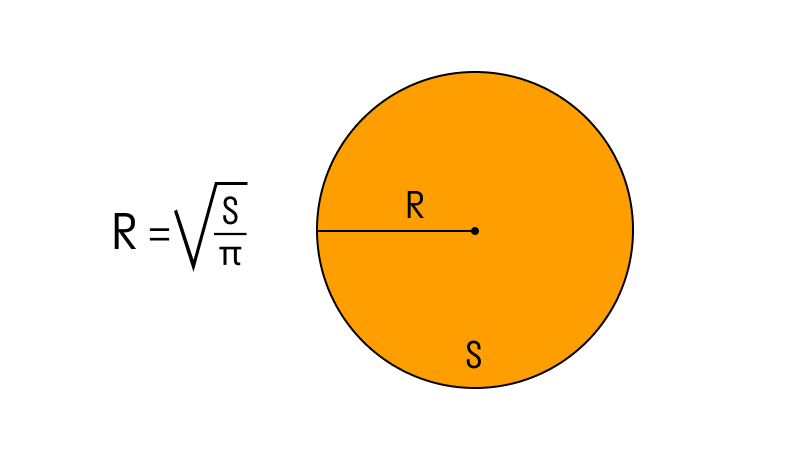
Если известна площадь круга
, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
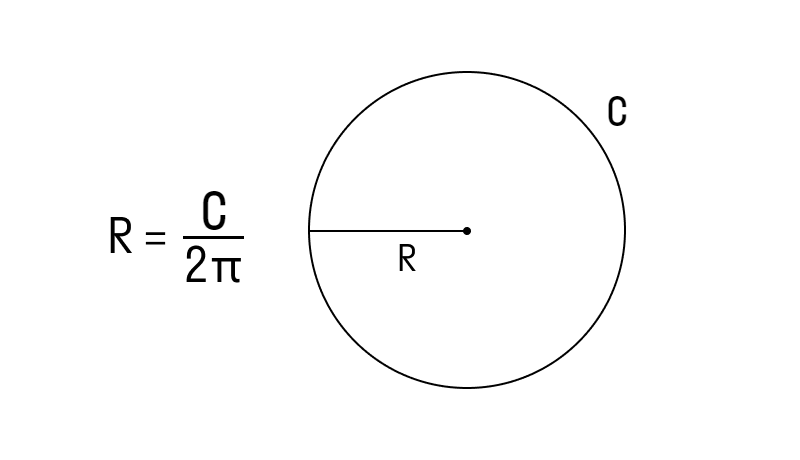
Если известна длина
, где C — длина окружности.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
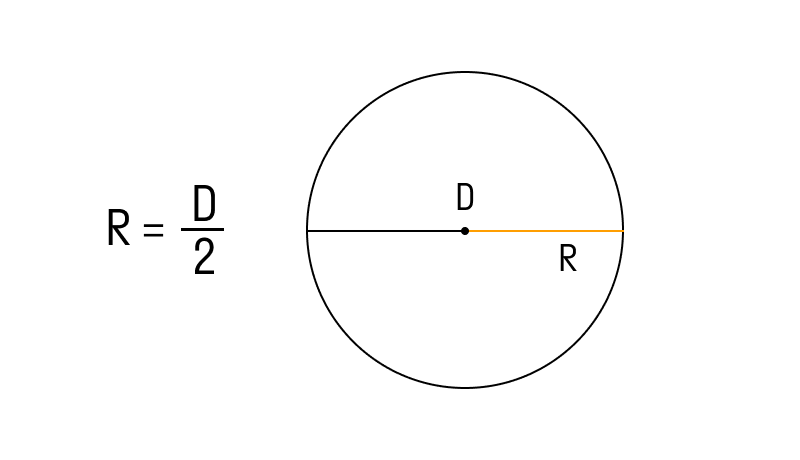
Если известен диаметр окружности
, где D — диаметр.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
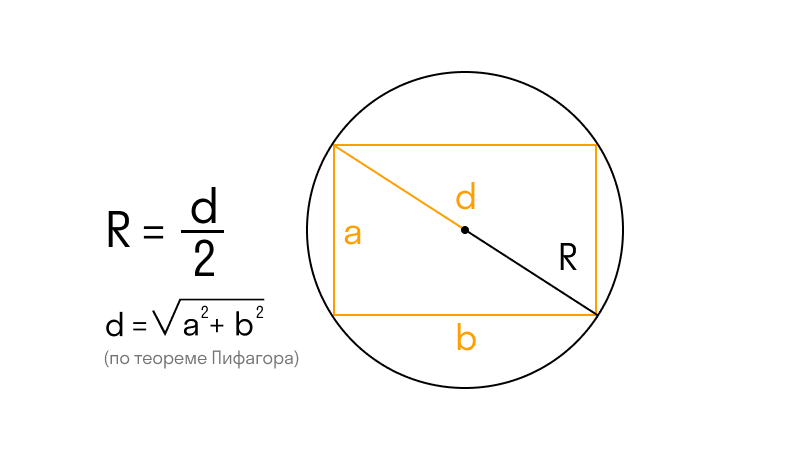
Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ прямоугольника.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
, где a, b — стороны вписанного прямоугольника.
Равносторонний треугольник

Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера»
| Равносторонний треугольник – треугольник, у которого все стороны равны. |
Какие же особенные свойства присущи равностороннему треугольнику?
Равносторонний треугольник. Свойства
| Свойство 1. В равностороннем треугольнике все углы равны между собой и равны . |
Естественно, не правда ли? Три одинаковых угла, в сумме , значит, каждый по .
| Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и серединных перпендикуляров совпадают – оказываются одной и той же точкой. И эта точка называется центром треугольника (равностороннего!). |
Почему так? А посмотрим-ка на равносторонний треугольник:
| Он является равнобедренным, какую бы его сторону ни принять за основание – так сказать, со всех сторон равнобедренный. |
Значит, любая высота в равностороннем треугольнике является также и биссектрисой, и медианой, и серединным перпендикуляром! В равностороннем треугольнике оказалось не особенных линий, как во всяком обычном треугольнике, а всего три!
Итак, ещё раз:
| Центр равностороннего треугольника является центром вписанной и описанной окружности, а также точкой пересечения высот и медиан. |
| Свойство 3. В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной. |
Уже должно быть очевидно, отчего так.
Посмотри на рисунок: точка – центр треугольника. Значит, – радиус описанной окружности (обозначили его ), а – радиус вписанной окружности (обозначим ).
Но ведь точка – ещё и точка пересечения медиан! Вспоминаем, что медианы точкой пересечения делятся в отношении , считая от вершины.
Поэтому , то есть .
| Свойство 4. В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны. |
Давай удостоверимся в этом.
Почему?
Рассмотрим – он прямоугольный.
.
А это почему?
Мы уже выяснили, что точка – не только центр описанной окружности, но и точка пересечения медиан. Значит, .
Величину мы уже находили. Теперь подставляем:
Это уже теперь должно быть совсем ясно
.
Ну вот, все основные сведения обсудили. Конечно, можно задавать сотни вопросов про всякие длины всяких отрезков в равностороннем треугольнике.
Но главное, что следует иметь в виду, решая задачки о равностороннем треугольнике, – это то, что все его углы известны – равны и все высоты являются и биссектрисами, и медианами, и серединными перпендикулярами.
Равносторонний треугольник. краткое изложение и основные формулы
Равносторонний треугольник – треугольник, у которого все стороны равны: .
|
|
В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны :
|
ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!
Стать учеником YouClever,
А также получить бессрочный доступ к учебнику “YouClever”, Программе подготовки (решебнику) “100gia”, неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.
Треугольник с равными сторонами
Каждый школьник, в каком бы классе он ни учился, знает, что собой представляет треугольник. Он является самой простой замкнутой фигурой на плоскости и в пространстве, поскольку образован тремя отрезками (четырьмя ограничены следующие по сложности за ним фигуры: прямоугольник, квадрат, параллелограмм и т. д. ).
Состоит он из трех сторон, которые определяют 3 его угла (отсюда и название геометрического объекта). Для определения значений углов в градусах следует при решении задач использовать теорему о равенстве их суммы — 180
При этом неважно, к какому типу относится сама фигура (равнобедренный, прямоугольный и т. д
), теорема остается справедливой всегда.
Исходя из названия, равносторонний треугольник — плоская фигура, все 3 стороны которой равны между собой. Для нее являются справедливыми следующие свойства:
- Все 3 угла равны между собой и составляют 60 градусов, поэтому его также называют равноугольным. Это утверждение справедливо в обратную сторону: если все углы треугольника составляют 60 градусов, он является равносторонним.
- Медиана, биссектриса и высота совпадают друг с другом, то есть любая из этих линий будет делить угол пополам, противоположную сторону на 2 равные части и будет перпендикулярна ей одновременно.
- Наличие трех осей симметрии. Все они совпадают с соответствующими медианами, биссектрисами, высотами. Оси пересекаются в точке, которая является геометрическим и массовым центром фигуры. Повороты на 0, 120, 240 и 360 градусов вокруг этой точки треугольника будут переводить его самого в себя, то есть являются операциями симметрии.
- Любые 2 рассматриваемых треугольника являются подобными. Этот вывод следует из равенства их трех углов.
Описанная окружность подробнее
Определение
Описанная окружность – такая окружность, что проходит через все три вершины треугольника, около которого она описана.
Свойства и центр описанной кружности
И вот, представь себе, имеет место удивительный факт:
Вокруг всякого треугольника можно описать окружность.
Почему этот факт удивительный?
Потому что треугольники ведь бывают разные!
И для всякого найдётся окружность, которая пройдёт через все три вершины, то есть описанная окружность.
Доказательство этого удивительного факта мы приведем чуть позже, а здесь заметим только, что если взять, к примеру, четырехугольник, то уже вовсе не для всякого найдётся окружность, проходящая через четыре вершины.
Вот, скажем, параллелограмм – отличный четырехугольник, а окружности, проходящей через все его четыре вершины – нет!
А есть только для прямоугольника:
Подробнее об этом смотри в статье о вписанных четырехугольниках!
Ну вот, а треугольник всякий и всегда имеет собственную описанную окружность! И даже всегда довольно просто найти центр этой окружности.
Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам этого треугольника.
Знаешь ли ты, что такое серединный перпендикуляр?
Серединный перпендикуляр — это прямая, проходящая через середину отрезка и перпендикулярная ему.
Прямая \( \displaystyle a\) – это серединный перпендикуляр к отрезку \( \displaystyle AB\).
А теперь посмотрим, что получится, если мы рассмотрим целых три серединных перпендикуляра к сторонам треугольника.
Вот оказывается (и это как раз и нужно доказывать, хотя мы и не будем), что все три перпендикуляра пересекутся в одной точке. Смотри на рисунок – все три серединных перпендикуляра пересекаются в одной точке \( \displaystyle O\).
Это и есть центр описанной около (вокруг) треугольника \( \displaystyle ABC\) окружности.
Как ты думаешь, всегда ли центр описанной окружности лежит внутри треугольника? Представь себе – вовсе не всегда!
Если треугольник тупоугольный, то центр его описанной окружности лежит снаружи!
Вот так:
А вот если остроугольный, то внутри:
Что же делать с прямоугольным треугольником?
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.
Здорово, правда?
Если треугольник – прямоугольный, то не надо строить аж три перпендикуляра, а можно просто найти середину гипотенузы – и центр описанной окружности готов!
Да ещё с дополнительным бонусом:
В прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы.
Раз уж заговорили о радиусе описанной окружности: чему он равен для произвольного треугольника? И есть ответ на этот вопрос: так называемая теорема синусов.
А именно:
В произвольном треугольнике:\( \Large \displaystyle \frac{a}{\sin \angle A}=2R\)
Ну и, конечно,
Так что ты теперь всегда сможешь найти и центр , и радиус окружности, описанной вокруг треугольника.
То есть чтобы найти радиус описанной окружности, нужно знать одну (!) сторону и один (!) противолежащий ей угол.
Хорошая формула? По-моему, просто отличная!
Составьте уравнение окружности вписанной в треугольник стороны которых лежат на прямых заданных уравнениями х = 0 у = 0 4х — 3у — 24 = 0?
Геометрия | 5 — 9 классы
Составьте уравнение окружности вписанной в треугольник стороны которых лежат на прямых заданных уравнениями х = 0 у = 0 4х — 3у — 24 = 0.
Х = 0 это ось оу, у = 0 — это ось ох.
4х — 3у — 24 = 0 построим данную прямую.
— 3у = 24 — 4х = — 8 + 4х / 3 или у = 4х / 3 — 8.
Это уравнение прямой, которая задается
При х = 0 у = — 8 при х = 3 у = — 4.
Эта прямая находится в 4
Провели декартову прямоугольную систему координат, навели
более жирным положительную ось ох, відємну ось оу, и по координатам
которые мы нашли построили третью прямую.
Его диаметр = 4, поскольку диаметр по правилу = от суммы
катетов надо — гипотенузу.
Координаты центра(2 ; — 2).
(х — 2) в квадрате + (у + 2)в квадрате = 4.
— Что такое формула радиуса? Примеры
Прежде чем мы начнем с формулы радиуса, давайте вспомним, что такое радиус.
Мы можем найти радиус круга, когда известны диаметр, площадь или длина окружности.
Формулы радиуса
Формула радиуса 1: Радиус равен половине длины диаметра. Если диаметр круга известен, то формула радиуса выражается следующим образом:
Формула радиуса = Диаметр/2 или D/2 единиц
Формула радиуса 2: Радиус – это отношение длины окружности к 2π. Если длина окружности известна, то формула радиуса выражается так:
Формула радиуса = длина окружности/2π или единиц C/2π
Формула радиуса 3: Мы можем вывести формулу радиуса, используя формулу площади круга, которая представляет собой Площадь = π(Радиус) 2 .
Формула радиуса = √(Площадь/π) единиц
Давайте изучим формулу радиуса на нескольких примерах решения.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Записаться на бесплатный пробный урок
Примеры формулы радиуса
Пример 1: Найдите радиус круга, диаметр которого составляет 24 дюйма. (Подсказка: используйте формулу радиуса, когда известен диаметр)
Решение: Мы будем использовать формулу радиуса, когда известен диаметр окружности. Что выражается как. Радиус = Диаметр/2 Г = 24 дюйма R = 24/2 = 12 дюймов Ответ: Радиус данной окружности равен 12 дюймам.
Пример 2: Найдите радиус круга, длина окружности которого составляет 4π единиц.
Решение: Мы будем использовать следующую формулу радиуса, чтобы найти радиус окружности. Радиус = Окружность/2π C = 4πединиц Радиус = 4π/2π = 2 единицы
Ответ: Радиус данной окружности равен 2 единицам.
Пример 3: Найдите радиус круга, площадь которого 4π единиц 2 . (Подсказка: используйте формулу радиуса, когда известна площадь круга)
Решение: Мы будем использовать следующую формулу радиуса, чтобы найти радиус круга. Формула радиуса = √(Площадь/π) Площадь = 4π единиц 2 R = √(4π/π) Радиус = 2 единицы
Ответ: Радиус данной окружности равен 2 единицам.
Что такое формула радиуса, когда известна площадь круга?
Если площадь круга указана в квадратных единицах, то легко вывести формулу радиуса, как показано ниже: Площадь = π(радиус) 2 Формула для радиуса = √(площадь/π) единиц
Если диаметр окружности дан в единицах «x», то легко вывести формулу радиуса, как указано ниже: Диаметр = 2р.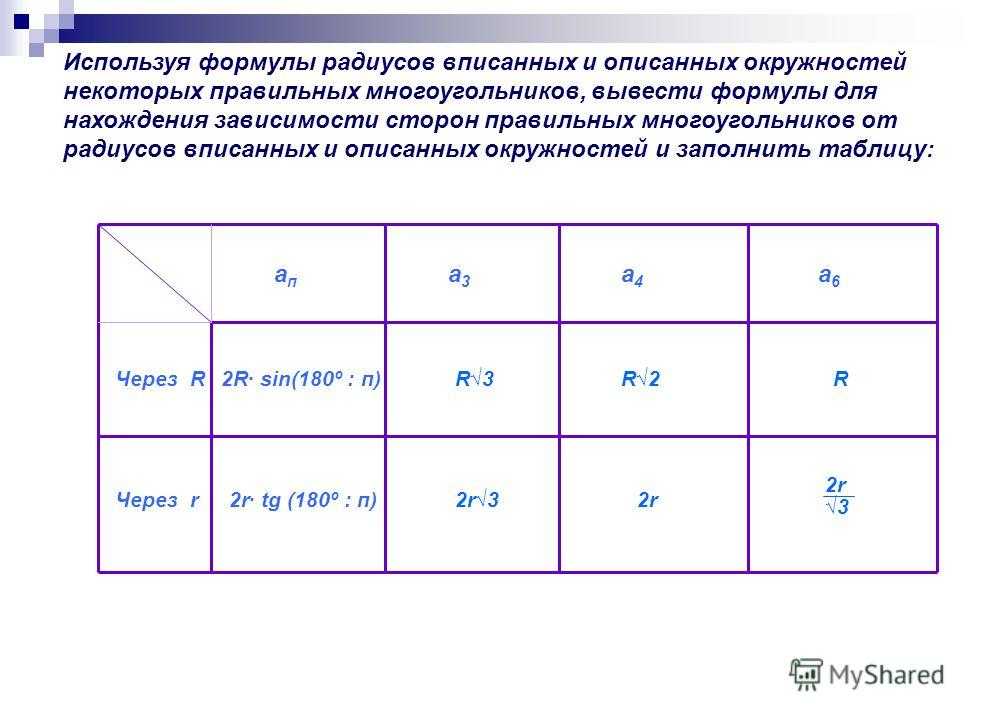
Что такое формула радиуса, когда известна длина окружности?
Если длина окружности дана в единицах x, то легко вывести формулу радиуса, как указано ниже: Окружность = 2πr. Формула для радиуса = длина окружности/2π единиц
Как найти длину окружности с помощью формулы радиуса?
Если задан радиус круга, то путем подстановки данных значений в следующую формулу радиуса мы можем легко найти длину окружности. Формула для радиуса = длина окружности/2π. C = 2πr единиц.
Задания №6. Задачи на комбинацию окружности и треугольника

Елена Репина 2013-07-28 2016-06-20
Задача 1
Площадь треугольника равна 800, а радиус вписанной окружности равен 16. Найдите периметр этого треугольника.
Решение: + показать
Задача проста, если знать формулу , где – радиус вписанной в треугольник окружности, – полупериметр треугольника.
Тогда
Ответ: 100.
Задача 2
Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 66.
Решение: + показать
Радиус вписанной окружности в правильный треугольник – есть высоты (), так в правильном треугольнике высоты совпадают с медианами, а медианы в точке пересечения делятся в отношении 2:1, считая от вершины.
Итак,
Ответ: 22.
Задача 3
Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.
Решение: + показать
Из предыдущей задачи мы знаем, что радиус вписанной окружности есть где – высота, медиана.
Из треугольника
Тогда
Ответ: 19.
Задача 4
В треугольнике ABC . Найдите радиус вписанной окружности.
Решение: + показать
Найдем гипотенузу по т. Пифагора:
Найдем площадь и периметр треугольника, чтобы воспользоваться затем формулой :
Тогда
Ответ: 1.
Задача 5
Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 11. Найдите гипотенузу c этого треугольника. В ответе укажите .
Решение: + показать
Воспользуемся формулой .
Пусть
Тогда
Далее, по т. Пифагора
Значит,
Итак, возвращаемся к формуле :
Так как по условию , то
Так как гипотенуза c () есть , то
Значит,
Ответ: 22.
Задача 6.
Боковые стороны равнобедренного треугольника равны 181, основание равно 38. Найдите радиус вписанной окружности.
Решение: + показать
Воспользуемся формулой Герона: , где – полупериметр, – стороны треугольника.
Ответ: 17,1.
Задача 7.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 13 и 5, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Решение: + показать
По свойству отрезков касательных, проведенных из одной точки к окружности, а поскольку – середина , то
Ответ: 46.
Задача 8.
К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 10, 18, 33. Найдите периметр данного треугольника.
Решение: + показать
Опять же, по свойству отрезков касательных, имеем: и т.д.
Значит,
Суммируем построчно последние три равенства:
Ответ: 61.
Задача 1.
Найдите радиус окружности, описанной около прямоугольного треугольника , если стороны квадратных клеток равны 1.
Решение: + показать
В прямоугольном треугольнике центр описанной окружности – середина гипотенузы. Радиус описаной окружности равен половине гипотенузы.
Ответ: 2,5.
Задача 2.
Боковые стороны равнобедренного треугольника равны 50, основание равно 60. Найдите радиус описанной окружности этого треугольника.
Решение: + показать
Воспользуемся следующей формулой:
Площадь будем искать по формуле Герона:
Тогда
Ответ: 31,25.
Задача 3.
Сторона AB треугольника ABC равна 28. Противолежащий ей угол C равен 150˚. Найдите радиус окружности, описанной около этого треугольника.
Решение: + показать
Согласно т. Синусов
Ответ: 28.
Задача 4.
Угол C треугольника ABC, вписанного в окружность радиуса 47, равен 30˚. Найдите сторону AB этого треугольника.
Решение: + показать
Задачу можно решить способом, которым решали предыдущую задачу (использую теорему синусов).
Рассмотрим другой способ решения:
Треугольник – равносторонний, так как центральный угол равен (ведь он соответствующий для вписанного угла, равного 30˚) и как радиусы (следовательно как равные углы при основании равнобедренного треугольника).
Стало быть,
Ответ: 47.
Задача 5.
В треугольнике ABC BC, угол C равен 90°. Радиус описанной окружности этого треугольника равен 17,5. Найдите AC.
Решение: + показать
В прямоугольном треугольнике гипотенуза – диаметр описанной окружности.
Значит,
По теореме Пифагора
Ответ: 30.
Формулы
1. Диаметр окружности (d):
2. Длина окружности (С):
3. Радиус окружности (R):
Публикации по теме:
- Нахождение площади квадрата: формула и примеры Нахождение площади прямоугольника: формула и пример Нахождение площади треугольника: формула и примеры Нахождение площади круга: формула и примеры Нахождение площади ромба: формула и примеры Нахождение площади эллипса: формула и пример Нахождение площади выпуклого четырехугольника: формула и пример Нахождение периметра квадрата: формула и задачи Нахождение периметра треугольника: формула и задачи Нахождение периметра параллелограмма: формула и задачи Нахождение длины окружности: формула и задачи Теорема Пифагора для прямоугольного треугольника: формула и задачи Теорема косинусов для треугольника: формула и задачи Теорема синусов для треугольника: формула и задачи Тригонометрические функции острого угла в прямоугольном треугольнике Нахождение объема конуса: формула и задачи Нахождение объема цилиндра: формула и задачи Нахождение площади правильного шестиугольника: формула и примеры Нахождение объема тетраэдра: формула и задачи Нахождение объема призмы: формула и задачи Нахождение объема параллелепипеда: формула и задачи Нахождение площади поверхности цилиндра: формула и задачи Нахождение площади поверхности конуса: формула и задачи Нахождение площади поверхности шара (сферы): формула и задачи Нахождение площади поверхности вписанного в цилиндр шара Нахождение радиуса цилиндра: формула и примеры Нахождение площади прямоугольного параллелепипеда: формула и пример Нахождение площади правильной пирамиды: формулы Теорема о внешнем угле треугольника: формулировка и задачи Теорема Чевы: формулировка и пример с решением Теорема Стюарта: формулировка и пример с решением Теорема о трех перпендикулярах Геометрическая фигура: треугольник Признаки равенства треугольников Признаки подобия треугольников Признаки равенства прямоугольных треугольников Свойства прямоугольного треугольника Определение и свойства медианы треугольника Определение и свойства медианы прямоугольного треугольника Определение и свойства медианы в равнобедренном треугольнике Определение и свойства медианы равностороннего треугольника Свойства биссектрисы прямоугольного треугольника Свойства биссектрисы равностороннего треугольника Определение и свойства высоты треугольника Свойства высоты равностороннего треугольника Нахождение радиуса описанной вокруг треугольника окружности Нахождение радиуса вписанной в треугольник окружности Что такое квадрат: определение и свойства Нахождение радиуса вписанной в квадрат окружности Нахождение радиуса описанной вокруг квадрата окружности
Радиус окружности (R) – это отрезок, соединяющий любую точку, лежащую на окружности, с ее центром.
Что такое окружность: определение, свойства, формулы
В данной публикации мы рассмотрим определение и свойства одного из основных геометрических объектов – окружности. Также приведем формулы, с помощью которых можно найти ее радиус, диаметр и длину.
скрыть
Через три точки на плоскости, не лежащие на одной прямой, можно провести окружность, причем только одну.
Свойство 2
Изопериметрическое неравенство Из всех замкнутых кривых одинаковой длины окружность ограничивает область с самой большой площадью.
09.12.2017 8:12:43
2017-12-09 08:12:43
Любые данныеЛюбые данные Любые данные Любые данные
Углы в окружности
Градусные меры центрального угла и дуги, на которую тот опирается, равны.
\angle COD = \cup CD = \alpha ^{\circ}
Вписанный угол
— это угол, вершина которого находится на окружности, а стороны содержат хорды.
Вычислить его можно, узнав величину дуги, так как он равен половине этой дуги.
\angle AOB = 2 \angle ADB
Опирающийся на диаметр, вписанный угол, прямой.
\angle CBD = \angle CED = \angle CAD = 90^ {\circ}
Вписанные углы, которые опираются на одну дугу, тождественны.
Опирающиеся на одну хорду вписанные углы тождественны или их сумма равняется 180^ {\circ}
.
\angle ADB + \angle AKB = 180^ {\circ}
\angle ADB = \angle AEB = \angle AFB
На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.
Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left (\cup DmC + \cup AlB \right)
Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left (\cup DmC — \cup AlB \right)
Ответ
Проверено экспертом
Центр вписанной окружности в равносторонний треугольник лежит на высоте (биссектрисе и медиане) и делит её в отношении 2/1 считая от вершины. ⇒ высота (7+7*2)=21 ед.
Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?
Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?
Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера»
| Равносторонний треугольник — треугольник, у которого все стороны равны. |
Какие же особенные свойства присущи равностороннему треугольнику?
Равносторонний треугольник. Свойства
| Свойство 1. В равностороннем треугольнике все углы равны между собой и равны . |
Естественно, не правда ли? Три одинаковых угла, в сумме , значит, каждый по .
| Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и серединных перпендикуляров совпадают – оказываются одной и той же точкой. И эта точка называется центром треугольника (равностороннего!). |
Почему так? А посмотрим-ка на равносторонний треугольник:
| Он является равнобедренным, какую бы его сторону ни принять за основание – так сказать, со всех сторон равнобедренный. |
Значит, любая высота в равностороннем треугольнике является также и биссектрисой, и медианой, и серединным перпендикуляром! В равностороннем треугольнике оказалось не особенных линий, как во всяком обычном треугольнике, а всего три!
Посоветуйте интересную книгу форум
| Центр равностороннего треугольника является центром вписанной и описанной окружности, а также точкой пересечения высот и медиан. |
| Свойство 3. В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной. |
Уже должно быть очевидно, отчего так.
Посмотри на рисунок: точка – центр треугольника. Значит, – радиус описанной окружности (обозначили его ), а – радиус вписанной окружности (обозначим ).
Но ведь точка – ещё и точка пересечения медиан! Вспоминаем, что медианы точкой пересечения делятся в отношении , считая от вершины.
Поэтому , то есть .
| Свойство 4. В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны. |
Давай удостоверимся в этом.
Рассмотрим – он прямоугольный.
Равносторонний треугольник. Радиус описанной окружности
Мы уже выяснили, что точка – не только центр описанной окружности, но и точка пересечения медиан. Значит, .
Величину мы уже находили. Теперь подставляем:
Равносторонний треугольник. Радиус вписанной окружности
Это уже теперь должно быть совсем ясно
Ну вот, все основные сведения обсудили. Конечно, можно задавать сотни вопросов про всякие длины всяких отрезков в равностороннем треугольнике.
Но главное, что следует иметь в виду, решая задачки о равностороннем треугольнике, – это то, что все его углы известны – равны и все высоты являются и биссектрисами, и медианами, и серединными перпендикулярами.
Равносторонний треугольник. краткое изложение и основные формулы
Равносторонний треугольник — треугольник, у которого все стороны равны: .
|
С чем можно поесть сгущенку
|
В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны :
|
Получить доступ к учебнику YouClever без ограничений можно кликнув по этой ссылке:
Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.
- Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
- Площадь треугольника равна произведению ПЕРИМЕТРА на радиус!
- Площадь треугольника равна произведению ПОЛУПЕРИМЕТРА на радиус вписанной окружности
Площадь треугольника равна 24, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника.
Из формулы , где p — полупериметр, находим, что периметр описанного многоугольника равен отношению удвоенной площади к радиусу вписанной окружности:
Равносторонний треугольник вписан в окружность найти радиус Ссылка на основную публикацию
Как найти радиус описанной окружности
Предположим, что a, b, c — это стороны треугольника. Если знать их величины, то можно найти радиус описанной вокруг него окружности. Для этого сначала нужно найти полупериметр треугольника. Чтобы было легче для восприятия, обозначим его маленькой буквой p. Он будет равен половине суммы сторон. Его формула: p = (a + b + c) / 2.
Также вычислим произведение длин сторон. Для удобства обозначим его буквой S. Формула радиуса описанной окружности будет выглядеть так: R = S / (4 * √(p * (p — a) * (p — b) * (p — c)).
Рассмотрим пример задачи. У нас есть окружность, описанная вокруг треугольника. Длины ее сторон составляют 5, 6 и 7 см. Сначала вычисляем полупериметр. В нашей задаче он будет равен 9 сантиметрам. Теперь вычислим произведение длин сторон — 210. Подставляем результаты промежуточных расчетов в формулу и узнаем результат. Радиус описанной окружности равен 3,57 сантиметра. Записываем ответ, не забывая о единицах измерения.
В окружность вписан правильный шестиугольник?
В окружность вписан правильный шестиугольник.
В него вписана окружность, в которую вписан правильный треугольник.
Найдите сторону треугольника, если диаметр большей окружности равен 4 см.
1 сторона это х 2 сторона это 7х 260 : 2 = 130 7х + х = 130 8х = 130 х = 130 : 8 х = 16, 25 значит 1 сторона равна 16, 25 а 2 сторона 113, 75.
Они все = 105° 1 и 2 в сумме дают 180, как смежные. 3 и 4 равны как вертикальные.
Что будет не пончтно, спрашивай).
1 Если ось вращения — длинная сторона, то радиус цилиндра — короткая сторона, 4 см 2 если осевое сечение конуса — равносторонний треугольник со стороной 12 см, то радиус конуса = 6 см Образующая 12 см, а высота по теореме Пифагора h ^ 2 = 12 ^ 2 — 6 ..
18 + 18 = 36 градусов, 360 — 36 = 324 градуса, 324 / 2 = 162 градуса. Ответ : 162 градуса.
Из треугольника полученного когда опустили высоту найдём острый угол 180 — 90 — 33 = 57. Теперь найдём тупой угол параллелограмма 180 — 57 = 123.
1x + 2x + 3x = 180 6x = 180 x = 30(A) 30 * 2 = 60(B) 30 * 3 = 90(C).
Выразить векторы через другие. Можно было КМ найти иначе и экономнее, но захотелось разнообразнее.
OA = OB = AB = > треугольник AOB равносторонний. У равностороннего треугольника равны все углы, а значит, что каждый равен 60°. Найдём смежный угол с углом AOC : COB = 120° (180° — 60°) Треугольник COB равнобедренный, т. К. OC = BO, если треугольн..
Диаметр описанной окружности
Диаметр описанной окружности также можно найти, если он описан или вписан в треугольник. Для этого сначала нужно найти радиус для вписанной окружности по формуле: R = S/p, где S обозначает площадь треугольника, а р – его полупериметр, p приравнивается к (a + b + c)/2. После того, как известен радиус, нужно воспользоваться первой формулой. Либо же сразу подставить все значения в формулу D = 2S/p.
Если вы не знаете, как найти диаметр описанной окружности, воспользуйтесь формулой, для нахождения радиуса окружности описанной около треугольника. R = (a * b * c)/4 * S, S в формуле обозначает величину площади треугольника. Потом, точно также подставьте значение радиуса в формулу D = 2R.
Тема «Вписанные и описанные окружности в треугольниках» является
одной из самых сложных в курсе геометрии. На уроках ей уделяется очень
мало времени.
Геометрические задачи этой темы включаются во вторую часть экзаменационной работы ЕГЭ за курс средней школы. Для
успешного выполнения этих заданий необходимы твердые знания основных
геометрических фактов и некоторый опыт в решении геометрических задач. Для каждого треугольника существует только одна описанная окружность.
Это такая окружность, на которой лежат все три вершины треугольника с
заданными параметрами. Найти ее радиус может понадобиться не только на
уроке геометрии. С этим приходится постоянно сталкиваться
проектировщикам, закройщикам, слесарям и представителям многих других
профессий. Для того, чтобы найти ее радиус, необходимо знать параметры
треугольника и его свойства. Центр описанной окружности находится в
точке пересечения серединных перпендикуляров треугольника.
Предлагаю вашему вниманию все формулы нахождения радиуса описанной окружности и не только треугольника. Формулы для вписанной окружности можно посмотреть .
a, b. с —
стороны треугольника,
α —
угол, лежащий против стороны
a,
S —
площадь треугольника
,
p —
полупериметр.
Тогда для нахождения радиуса (R
) описанной окружности используют формулы:
В свою очередь площадь треугольника можно вычислить по одной из следующих формул:
А вот еще несколько формул.
1. Радиус описанной окружности около правильного треугольника. Если a
сторона треугольника, то
2. Радиус описанной окружности около равнобедренного треугольника. Пусть a, b
— стороны треугольника, тогда
Введение.
Тема «Вписанные и описанные окружности в треугольниках» является одной из самых сложных в курсе геометрии. На уроках ей уделяется очень мало времени.
Геометрические задачи этой темы включаются во вторую часть экзаменационной работы ЕГЭ за курс средней школы.Для успешного выполнения этих заданий необходимы твердые знания основных геометрических фактов и некоторый опыт в решении геометрических задач.
Теоретическая часть.
Описанная окружность многоугольника
— окружность, содержащая все вершины многоугольника. Центром является точка (принято обозначать O) пересечения серединных перпендикуляров к сторонам многоугольника.
Свойства.
Центр описанной окружности выпуклого n-угольника лежит в точке пересечения серединных перпендикуляров к его сторонам. Как следствие: если рядом с n-угольником описана окружность, то все серединные перпендикуляры к его сторонам пересекаются в одной точке (центре окружности).Вокруг любого правильного многоугольника можно описать окружность.
Для треугольника.
Окружность называется описанной около треугольника, если она проходит через все его вершины.
Вокруг любого треугольника можно описать окружность, притом только одну
. Её центром будет являться точка пересечения серединных перпендикуляров.
У остроугольного треугольника центр описанной окружности лежит внутри
, у тупоугольного — вне треугольника
, у прямоугольного — на середине гипотенузы
.
Радиус описанной окружности может быть найден по формулам:
Где:
a,b,c
— стороны треугольника,α
— угол, лежащий против стороны a,S
— площадь треугольника.
Доказать:
т.О — точка пересечения серединных перпендикуляров к сторонам ΔABC
Доказательство:
- ΔAОC — равнобедренный, т.к. ОА=ОС (как радиусы)
- ΔAОC — равнобедренный, перпендикуляр OD — медиана и высота, т.е. т.О лежит на серединном перпендикуляре к стороне АС
- Аналогично доказывается, что т.О лежит на серединных перпендикулярах к сторонам АВ и ВС
Что и требовалось доказать.
Замечание.
Прямую, проходящую через середину отрезка перпендикулярно к нему, часто называют серединным перпендикуляром. В связи с этим иногда говорят, что центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам треугольника.
Доказательства теорем о свойствах описанной около треугольника окружности
Касательная к окружности
Касательной к окружности
принято называть прямую, у которой имеется одна общая точка с окружностью.
Если же у прямой есть две общие точки, ее называют секущей
.
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
AC = CB
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть.
AC^{2} = CD \cdot BC
Можно сделать вывод: произведение целого отрезка первой секущей на его внешнюю часть равняется произведению целого отрезка второй секущей на его внешнюю часть.
AC \cdot BC = EC \cdot DC
Вневписанная окружность
Ну вот, пора приступать к самому непонятному. Что же это за зверь такой: «вневписанная окружность»? Сначала посмотри на картинку:
Видишь, окружность тоже чего-то касается, но «сидит» как-то снаружи, вне треугольника? Вот поэтому и называется вневписанной.
Окружность называется вневписанной для треугольника, если она касается ОДНОЙ стороны треугольника и продолжений двух других сторон.
А как ты думаешь, сколько у одного треугольника может быть вневписанных окружностей? Вот, представь себе, аж три!
Посмотри, вот так:
Захватывает дух? Насладись впечатлением.
А еще подумай над тем…
- откуда взялся \( \displaystyle \Delta {{O}_{1}}{{O}_{2}}{{O}_{3}}\);
- что это за точка \( \displaystyle O\);
- что это вообще за тьма линий на рисунке.
А сейчас вернёмся к однойкакой-нибудь вневписанной окружности и узнаем всего один, но очень важный факт:



























