Окружность и круг: основные формулы

Относительное положение двух окружностей

Концентрические и эксцентрические круги. Два круга называются концентрическими, когда они имеют один общий центр, и эксцентрическими, когда из центры не совпадают.

На чертеже 96 представлены круги концентрические и на чертежах 97, 98, 99, 100 и 101 круги эксцентрические.

Внешние и внутренние круги. Круги называются внешними, когда все точки одного лежат вне площади другого круга, и внутренними, когда все точки одного лежат внутри площади другого круга.

На чертежах 97 и 99 изображены круги внешние, на чертежах 96, 98 и 100 круги внутренние.

Касательные окружности. Окружности называются касательными, когда они имеют одну общую точку.

Общая точка двух касательных окружностей называется их точкой соприкосновения. Соприкосновение называется внешним, когда два круга, имея общую точку, лежат один вне другого, и внутренним, когда один круг лежит внутри другого. На черт. 99 имеем случай внешнего, а на чертеже 100 случай внутреннего соприкосновения.

Пересекающиеся окружности. Окружности называются пересекающимися, когда они имеют две общие точки (черт. 101).

Линия центров есть отрезок, соединяющий центры двух кругов.

Теорема 71. Две окружности, имеющие общую точку на линии центров, другой общей точки иметь не могут.

Дано. Две окружности с центрами O и O’ имеют общую точку A (черт. 102).

Требуется доказать, что другой общей точки у них нет.

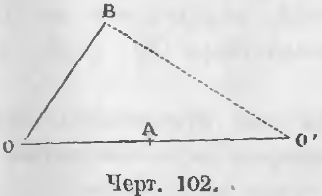
Доказательство. Положим, существует другая общая точка B, следовательно,

OB = OA и O’B = O’A.

Складывая эти равенства, мы имели бы

OB + O’B = OA + O’A или
OB + O’B = OO’

равенство несообразное, ибо ломаная не может равняться прямой.

Итак, другой общей точки быть не может (ЧТД).

Теорема 72. Две окружности, имеющие одну общую точку вне линии центров, имеют и другую общую точку по другую сторону линии центров.

Дано. Две окружности, центры которых O и O’, имеют общую точку A вне отрезка OO’ (черт. 103), соединяющей центры.

Требуется доказать, что существует и другая общая точка по другую сторону центров.

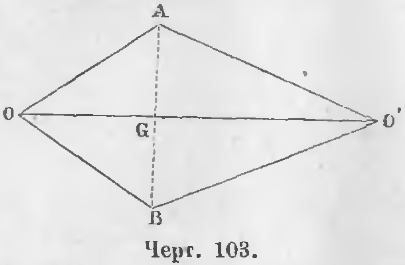
Доказательство. Из точки A опустим на линию центров перпендикуляр AG и на продолжении его отложим отрезок BG, равный AG.

Докажем, что точка B будет другая общая точка. Точка B лежит на окружности O, ибо AO = BO как равные наклонные, находящиеся на равных расстояниях AG и BG от перпендикуляра OO’. Точка B лежит на окружности O’, ибо AO’ = BO’ как равные наклонные, находящиеся на равных расстояниях AG и BG от перпендикуляра OO’, следовательно, точка B есть другая общая точка (ЧТД).

Теорема 73. Если две окружности пересекаются в двух точках, то линия центров перпендикулярна и делит пополам хорду, соединяющую точки пересечения.

Дано. Точки A и B есть точки пересечения (черт. 104) двух окружностей.

Требуется доказать, что AG = BG и AB ⊥ OO’.

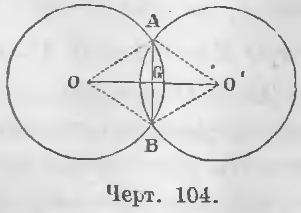
Доказательство. Треугольники OAO’ и OBO’ равны, ибо OO’ сторона общая.

OA = OB как радиусы окружности O.

O’A = O’B как радиусы окружности O’.

Следовательно,

∠AOO’ = ∠BOO’

Треугольники AOG и BOG равны, ибо OG сторона общая, AO = BO как радиусы, ∠AOG = ∠BOG по доказанному. Следовательно, AG = BG (хорда AB делится линией центров пополам), ∠AGO = ∠BGO (хорда AB перпендикулярна к линии центров).

Таким образом, хорда AB делится пополам и перпендикулярна к линии центров OO’ (ЧТД).

❓Вопросы и ответы

И наконец, предлагаем вам прочитать ответы на некоторые часто задаваемые вопросы относительно вычисления длины окружности.

Что что имеет большее значение радиус, диаметр, длина окружности или площадь круга?

Площадь круга. А если выставить всё это по мере убывания, то рейтинг будет таким:

• Площадь круга
• Длина окружности
• Диаметр
• Радиус

Какие есть ещё калькуляторы для круга у вас на сайте?

У нас есть разные калькуляторы, в частности калькуляторы: диаметра, площади круга и длины окружности. Для последней калькулятор находится наверху данной страницы.

Почему Пи равняется 3,1415926…, а не является «ровным» числом?

Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.

Хватит ли чего-то одного (диаметра, радиуса, площади) для расчёта длины окружности?

Да, хватит. Формулы и примеры расчетов периметра круга, в которых используется что-то одно из перечисленного, есть выше на данной странице.

Длина окружности (периметр круга)

Будем выводить длину произвольной окружности \(C \)
с помощью её радиуса, равного \(τ \)
.

Будем рассматривать две произвольные окружности. Обозначим их длины через \(C \)
и \(C» \)
, у которых радиусы равняются \(τ \)
и \(τ» \)
. Будем вписывать в эти окружности правильные \(n \)
-угольники, периметры которых равняются \(ρ \)
и \(ρ» \)
, длины сторон которых равняются \(α \)
и \(α» \)
, соответственно. Как мы знаем, сторона вписанного в окружность правильного \(n \)
– угольника равняется

\(α=2τsin\frac{180^0}{n} \)

Тогда, будем получать, что

\(ρ=nα=2nτ\frac{sin180^0}{n} \)

\(ρ»=nα»=2nτ»\frac{sin180^0}{n} \)

\(\frac{ρ}{ρ»}=\frac{2nτsin\frac{180^0}{n}}{2nτ»\frac{sin180^0}{n}}=\frac{2τ}{2τ»} \)

Получаем, что отношение \(\frac{ρ}{ρ»}=\frac{2τ}{2τ»} \)
будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть

\(\lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{2τ}{2τ»} \)

С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть \(n→∞ \)
), будем получать равенство:

\(lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{C}{C»} \)

Из последних двух равенств получим, что

\(\frac{C}{C»}=\frac{2τ}{2τ»} \)

\(\frac{C}{2τ}=\frac{C»}{2τ»} \)

Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть

\(\frac{C}{2τ}=const \)

Эту постоянную принять называть числом «пи» и обозначать \(π \)
. Приближенно, это число будет равняться \(3,14 \)
(точного значения этого числа нет, так как оно является иррациональным числом). Таким образом

\(\frac{C}{2τ}=π \)

Окончательно, получим, что длина окружности (периметр круга) определяется формулой

\(C=2πτ \)

В вашем браузере отключен Javascript. Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.

Узнать длину окружности

Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.

Рассчитать площадь шара

Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.

Вычислить объем шара

Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы
, понятия и определения требуются для этого.

Радиус и диаметр окружности

Диаметр окружности — это отрезок, который соединяет две любые точки окружности, причем сам отрезок должен проходить через центр окружности

Eсли от центра окружности провести отрезки ко всем точкам окружности, то они будут иметь одинаковую длину, то есть равны. В математике такие отрезки называют радиусами.

Все радиусы окружности, как и диаметры окружности, равны между собой, имеют одинаковую длину.

На рисунке выше изображена окружность, с центром в точке O. OA = OB = OC — радиусы окружности; BC = CO + OB — диаметр окружности;

Радиус окружности принято обозначать маленькой либо большой буквой, r или R. Диаметр окружности обозначают буквой D.

Диаметр окружности условно состоит из двух радиусов и равен длинам этих радиусов.

Длину радиуса окружности можно найти через диаметр окружности. Для этого достаточно разделить на два длину диаметра окружности, получившееся число и будет радиусом.

Формула радиуса окружности через диаметр:

Формула диаметра окружности через радиус:

Также, окружность, может быть вписанной в фигуру, описанной около фигуры; или вообще может быть не вписана и не описана. Формула радиуса окружности зависит от того находится фигура внутри окружности, или окружность находится около фигуры.

Существует радиус вписанной окружности и радиус описанной окружности.

Формулы радиуса вписанной и радиуса описанной окружностей зависят в первую очередь от геометрической фигуры.

Радиус описанной окружности — это радиус окружности, которая описана около геометрической фигуры.

Третий важный элемент геометрии — это поверхности

Поверхности, как и линии бывают разными, причем разнообразие поверхностей еще больше, чем линий.

3.1. Элементарная поверхность

Основная характеристика элементарной поверхности — площадь и вообще можно назвать элементарную поверхность элементарной частью площади. Для определения площади элементарной поверхности недостаточно знать только длину, необходимо оперировать еще и шириной. Таким образом элементарная поверхность — это уже элемент двухмерного мира. Как и линия, поверхность образована точками, минимум тремя, или линиями, как минимум тремя. Но с точки зрения классической геометрии это не совсем так. В геометрии Эвклида поверхность качественно новый элемент геометрии, связанный с предыдущими тем, что поверхность ограничивается линиями, поэтому определение поверхности как некоего элемента главная характеристика которого — площадь, вполне допустима.

3.2. Из элементарных поверхностей может слагаться поверхность сколь угодно большой площади

При этом как и в случае с линиями рассматривать все расстояния между точками вовсе не обязательно и даже расстояния между всеми линиями, которые могут быть образованы из этих точек — тоже не обязательно. Достаточно знать характеристики главных линий, я бы назвал эти линии характерными линиями. Характерные линии ограничивают поверхность, например черный квадрат Малевича ограничен 4 линиями.

3.3. Самая простая поверхность — плоская поверхность или как сейчас говорят — плоскость

Плоскость двухмерна, это означает, что плоскость всегда можно расположить так, что наблюдателю будет видна только одна линия. Например, плотники с древнейших времен проверяют точность обработки деревянного бруса, смотря на исследуемую поверхность так, чтобы линия, ограничивающая начало поверхности, совпала с линией, ограничивающей конец поверхности.

Плоскость — это частный случай всех возможных плоскостей, но как и прямая линия, плоскость очень важна для решения задач геометрии. Более того, прямая линия и плоскость интуитивно понятны даже людям, никогда геометрию не изучавшим. Например, когда человеку нужно добраться из точки А в точку В, то он старается проложить маршрут, максимально близкий к прямой линии, а если путь будет проходить по равнине, а не по пересеченной местности, то совсем хорошо. А еще люди делают тоннели в горах и засыпают овраги, чтобы сделать дорогу из одного пункта в другой максимально приближающейся к прямой линии.

И точка и линия и поверхность в геометрии могут рассматриваться и как отдельные элементы и как формообразующие элементы, например, точка формообразующий элемент для линии, а линия формообразующий элемент для поверхности. Также точка, линия и поверхность могут быть общими элементами геометрических фигур.

Для основной части школьного курса геометрии этих элементов вполне достаточно, да и у Евклида трехмерные геометрические фигуры рассматриваются в книгах XI-XIII. Тем не менее хочется закончить этот ряд.

Отношения со вписанными углами

Углы, вписанные в окружность, подчиняются следующим правилам:

1. Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.
2. Если два вписанных в круг угла опираются на одну и ту же линию, но их вершины расположены по разные стороны этой прямой, то сумма таких углов будет равняться 180 градусам.
3. Если два угла — центральный и вписанный — опираются на единую линию, и их вершины располагаются по одну сторону от неё, то величина вписанного угла будет равняться половине центрального.
4. Вписанный угол, который опирается на диаметр круга, является прямым.
5. Равные между собой по размеру отрезки стягивают равные центральные углы.
6. Чем больше величина стягивающего отрезка, тем больше величина центрального угла, который она стягивает. И наоборот, меньшая по размеру линия стягивает меньший центральный угол.
7. Чем больше центральный угол, тем больше величина отрезка прямой, который его стягивает.

Измерение углов

Центральные углы. Углы, имеющие вершину при центре, называются центральными углами.

Относительно этих углов имеют место следующие теоремы.

Теорема 74. Равным центральным углам в одной и той же окружности соответствуют равные дуги.

Дано. Углы AOB и COD равны (черт. 109).

Требуется доказать, что ◡AB = ◡CD.

Доказательство. Проведем хорды AB и CD и соединим точки A, B, C, D с центром. Два треугольника AOB и COD равны, ибо AO = CO и BO = DO как радиусы, ∠AOB = ∠COD по условию. Следовательно, хорды AB и CD равны.

Против равных хорд лежат равные дуги, следовательно и дуги AB и CD равны: ◡AB = ◡CD (ЧТД).

Теорема 75 (обратная 74). Равным дугам в одной и той же окружности соответствуют равные углы.

Дано. Дуги AB и CD равны (черт. 109).

Требуется доказать, что ∠AOB = ∠COD.

Доказательство. Из того, что дуги AB и CD равны, следует, что и хорды AB и CD тоже равны (теорема 61).

Два треугольника AOB и COD равны, ибо AB = CD как равные хорды, AO = CO и BO = DO как радиусы. Следовательно, ∠AOB = ∠COD (ЧТД).

Теорема 76. Отношение центральных углов равно отношению соответствующих им дуг.

Даны два центральные угла AOB и COD (черт. 110).

Требуется доказать, что

AOB/COD = AB/CD.

Доказательство. Здесь имеют место два случая:

1) Когда дуги AB и CD соизмеримы и 2) когда они несоизмеримы.

1-й случай. Дуги AB и CD соизмеримы.

Пусть дуга AE будет их общей мерой. Положим, что она p раз содержится в дуге AB и q раз в дуге CD. Разделив дугу AB на p, а CD на q равных частей и соединив точки деления дуг с центром O, мы разделим угол AOB на p, а угол COD на q равных углов, из которых каждый равен углу AOE.

Из равенств

AB = pAE, CD = qAE
AOB = pAOE, COD = qAOE

получаем

AOB/COD = p/q, AB/CD = p/q, откуда
AOB/COD = AB/CD (ЧТД).

2-й случай. Дуги AB и CD несоизмеримы.

Отложим дугу AF равную CD и соединим F с O. Углы AOF и COD равны.

Требуется доказать, что

AOB/AOF = AB/AF

Доказательство. A) Положим

AOB/AOF > AB/AF (1).

Для того, чтобы имело место равенство, нужно дробь во второй части неравенства (1) увеличить. Для этого следует ее знаменатель уменьшить.

Положим, мы нашли, что имеет место равенство

AOB/AOF = AB/AG (a)

Разделим дугу AB на равное число таких частей, чтобы каждая часть была менее GF; тогда одна из точек деления i упадет в промежутке между G и F. Дуги AB и Ai соизмеримы, следовательно,

AOB/AOi = AB/Ai (b).

Разделив равенства (b) на (a), находим

AOF/AOi = AG/Ai

равенство несообразное, ибо первая часть его больше, а вторая меньше 1, следовательно, допущение (1) не имеет места.

B) Допустим, что

AOB/AOF < AB/AF (2)

Тогда вторую часть этого неравенства нужно уменьшить для того, чтобы имело место равенство. Для этого нужно знаменатель дроби AB/AF увеличить. Положим, мы нашли такую точку H, чтобы удовлетворялось равенство

AOB/AOF = AB/AH (c)

Разделив дугу AB на такие равные части, чтобы каждая часть была меньше FH, мы найдем, что одна из точек деления J упадет в промежуток между F и H. Дуги AB и AJ будут соизмеримы, следовательно,

AOB/AOJ = AB/AJ (d)

Разделив равенство (d) на (c) найдем

AOF/AOJ = AH/AJ

Это равенство несообразно, ибо первое отношение меньше, а второе больше единицы, следовательно, и допущение (2) тоже не имеет места, откуда видно, что справедливо только равенство AOB/AOF = AB/AF (ЧТД).

Зная, что отношение углов равно отношению дуг, описанных равными радиусами, мы в пропорции (черт. 111)

AOB/COD = AB/CD

можем принять за единицу любую дугу. В этом случае должны принять за единицу и соответствующий ей угол.

Принимая дугу CD, а следовательно, и угол COD за 1, имеем равенство

AOB/1 = AB/1

или отношение угла к своей единице равно отношению дуги к своей соответствующей единице, откуда

∠AOB = ◡AB.

Это равенство означает, что

числовая величина угла равна числовой величине дуги, или что угол измеряется дугой, описанной из его вершины, как из центра.

Радиус и периметр окружности

Окружность – это геометрическая фигура, состоящая из всех точек на плоскости, расположенных на одинаковом расстоянии (радиусе) от одной точки (центра). Радиус (r) – это расстояние от центра окружности до любой точки окружности. Каждая окружность имеет свой радиус.

Периметр – это сумма длин всех границ фигуры. Для окружности периметр называется длиной окружности и обозначается символом (L). Длина окружности – это расстояние вдоль границы окружности между двумя точками. У окружности длина всегда больше, чем ее диаметр (2r).

Формула длины окружности L=2πr, где π (пи) – это математическая константа, равная примерно 3,14. При помощи этой формулы можно легко рассчитать длину окружности по заданному радиусу. Например, если радиус окружности равен 5 см, то ее длина будет L=2×3,14×5=31,4 см.

Значение константы π является бесконечной десятичной дробью, которая не может быть записана конечным числом знаков. Отсюда следует, что длина окружности также будет бесконечной десятичной дробью при использовании точных значений радиуса и π.

Таким образом, радиус и длина окружности – это важные понятия в геометрии. Радиус определяет форму окружности, а длина окружности помогает определить периметр фигуры. Формула L=2πr позволяет легко вычислить длину окружности, используя значение радиуса и константу π.

Примечания[править | править код]

1. ↑ диаметр // Этимологический словарь русского языка = Russisches etymologisches Wörterbuch : в 4 т. / авт.-сост. М. Фасмер ; пер. с нем. и доп. чл.‑кор. АН СССР О. Н. Трубачёва, под ред. и с предисл. проф. Б. А. Ларина . — Изд. 2-е, стер. — М. : Прогресс, 1986—1987.
2. ↑ Большаков В. П., Тозик В. Т., Чагина А. В. Инженерная и компьютерная графика. — СПб.: БХВ-Петербург, 2013. — 288 с. — ISBN 978-5-9775-0422-5. — С. 90.
3. ↑ The Unicode Standard, Version 13.0. Miscellaneous Technical, Range: 2300–23FF (англ.) (PDF). Unicode Inc (2020). Дата обращения: 6 сентября 2020. Архивировано 30 декабря 2019 года.
4. ↑ Monniaux, David UTF-8 (Unicode) compose sequence (англ.). — Файл конфигурации вводимых с помощью клавиши Compose символов. Дата обращения: 6 сентября 2020. Архивировано 3 августа 2020 года.
5. ↑ SYMBOL Characters and Glyphs. Дата обращения: 6 сентября 2020. Архивировано 6 августа 2020 года.

Применение в геометрии:

Окружность – это геометрическая фигура, состоящая из всех точек, которые находятся на одинаковом расстоянии от фиксированной точки, называемой центром окружности. Диаметр окружности – это отрезок, соединяющий две точки на окружности и проходящий через ее центр.

Применение понятия диаметра в геометрии очень широко. Вот некоторые его применения:

• Вычисление длины окружности: длина окружности равна произведению диаметра на число Пи (π). Формула для вычисления длины окружности: L = πd.
• Вычисление площади окружности: площадь окружности равна произведению квадрата диаметра на число Пи, разделенное на 4. Формула для вычисления площади окружности: S = (πd^2)/4.
• Решение задач на построение: зная диаметр окружности и ее центр, можно построить окружность с помощью циркуля и линейки.
• Вычисление других характеристик окружности: зная диаметр окружности, можно вычислить ее радиус, а также найти координаты точек на окружности.

Использование диаметра окружности в геометрии позволяет решать различные задачи, связанные с этой геометрической фигурой.

Диаметр и радиус:

Диаметр окружности — это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Он является самой длинной хордой окружности и делит ее на две равные полуокружности.

Диаметр обозначается символом «d» и является основным параметром для описания окружности. Он является удобным инструментом для измерения размеров и нахождения связанных с окружностью величин.

Радиус окружности — это отрезок, который соединяет центр окружности с любой точкой на ее границе. Радиус обозначается символом «r» и является одним из основных параметров, определяющих окружность.

Соотношение между диаметром и радиусом можно выразить следующим образом:

Параметр	Обозначение	Связь
Радиус	r	r = d/2
Диаметр	d	d = 2r

Таким образом, диаметр окружности всегда равен удвоенному радиусу.

Знание диаметра и радиуса окружности необходимо для решения различных задач, связанных с геометрией и физикой. Они позволяют вычислить площадь и длину окружности, а также определить расстояние между точками на окружности или плоскости.

Диаметр и длина окружности:

Диаметр окружности является одной из основных характеристик окружности. Это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Диаметр окружности обозначается символом d и является удвоенной длиной радиуса. То есть, если радиус окружности равен r, то диаметр будет равен 2r.

Диаметр окружности является важным параметром при расчете различных характеристик исследуемых объектов или при проведении измерений.

Что такое длина окружности?

Длина окружности — это расстояние, которое нужно пройти по окружности, чтобы вернуться в исходную точку. Она обозначается символом L или C. Длину окружности можно вычислить по формуле: L = πd, где π (пи) — это математическая константа, приближенное значение которой равно 3.14159, а d — диаметр окружности.

Важно отметить, что длина окружности зависит только от диаметра и не зависит от положения или размеров самой окружности. Это свойство позволяет использовать длину окружности в различных математических и физических расчетах

Вписанная окружность

Окружность называетсявписанной в многоугольник, если она касается его сторон. Центр вписанной окружности лежит в точке пересечения биссектрис углов многоугольника.

Не во всякий многоугольник можно вписать окружность.

Площадь многоугольника, в который вписана окружность можно найти по формуле

,

здесь — полупериметр многоугольника, — радиус вписанной окружности.

Отсюда радиус вписанной окружности равен

Если в выпуклый четырехугольник вписана окружность, то суммы длин противоположных сторон равны. Обратно: если в выпуклом четырехугольнике суммы длин противоположных сторон равны, то в четырехугольник можно вписать окружность:

В любой треугольник можно вписать окружность, притом только одну. Центр вписанной окружности лежит в точке пересечения биссектрис внутренних углов треугольника.

Радиус вписанной окружности равен
. Здесь

Обруч и окружность

Вспомним один из предметов инвентаря художественной гимнастики – обруч. Это узкое кольцо большого диаметра, внутри которого ничего нет. Обруч состоит только из «наброска», то есть из того же кольца. Именно с помощью обруча мы подходим к термину «окружность”.

Окружность – это замкнутая кривая, все точки которой равноудалены от центра.

Рассмотрим подробнее, что означает фраза «равноудален от центра». Предположим, мы точно знаем, где находится центр нашего кольца, и через этот центр мы протянем много-много лент. Тогда получается, что длина каждой полосы от середины до обруча будет одинаковой.

То есть окружность состоит из бесконечного числа точек, находящихся на равном расстоянии от центра.

Окружность и круг: основные различия

В геометрии окружность и круг смыслово связаны, но имеют некоторые отличия. Окружность — это геометрическая фигура, представляющая собой линию, состоящую из всех точек, равноудаленных от центра. Круг же — это теоретическая плоская фигура, ограниченная окружностью.

Главным отличием между окружностью и кругом является то, что окружность не имеет площади, в то время как круг — это круглая фигура с определенной площадью. Круг может быть задан с помощью радиуса и центра, который является точкой внутри круга.

Другое различие между окружностью и кругом заключается в их диаметрах. Диаметр — это отрезок, соединяющий две точки на окружности и проходящий через центр круга. В окружности диаметром считается любой отрезок, проходящий через центр, в то время как в круге диаметр — это двойной радиус.

Таким образом, главная разница между окружностью и кругом заключается в том, что окружность является линией, состоящей из точек, равноудаленных от центра, в то время как круг — это ограниченная этой окружностью плоская фигура с определенной площадью. Кроме того, окружность не имеет площади, в отличие от круга.

Определение и форма

Окружность и круг — две понятия из области геометрии, которые отличаются друг от друга. Окружность — это геометрическая фигура, состоящая из множества точек, которые находятся на одинаковом расстоянии от центра. Центр окружности — это точка, от которой все точки окружности расположены на одинаковом расстоянии, называемом радиусом.

Теория окружностей в геометрии изучает их свойства и особенности. Окружность является формой, которая не имеет начала и конца, она представляет собой замкнутую линию, состоящую из бесконечного числа точек.

Круг — это закрашенная фигура, которая образуется при закрашивании внутренней части окружности. Круг представляет собой плоскую геометрическую фигуру, ограниченную окружностью. Диаметр круга — это отрезок, соединяющий две точки на окружности круга и проходящий через его центр. Диаметр является максимальной длиной от точки к точке на окружности.

В качестве иллюстрации можно представить таблицу с описанием различий между окружностью и кругом:

Окружность	Круг
Геометрическая фигура	Закрашенная фигура
Бесконечная линия	Ограниченная плоская фигура
Состоит из множества точек на одинаковом расстоянии от центра	Состоит из закрашенной области внутри окружности
Центр и радиус определяют окружность	Центр и радиус определяют круг, а также диаметр

Что такое окружность?

Окружность – это геометрическая фигура, которая представляет собой замкнутую линию на плоскости. Она состоит из всех точек, расположенных на одинаковом расстоянии от определенной точки, которую называют центром окружности.

Один из основных параметров окружности – это радиус, который определяет расстояние от центра до любой точки на окружности. Также можно выразить радиус через диаметр окружности. Диаметр – это отрезок, проходящий через центр окружности и соединяющий две противоположные точки на окружности.

Окружность можно охарактеризовать свойствами ее периметра и площади. Периметр окружности вычисляется по формуле 2πr, где r – радиус окружности. Площадь окружности вычисляется по формуле πr².

Чтобы иллюстрировать свойства окружности и ее параметры, можно использовать таблицу или графические примеры. Например, в таблице можно привести значения радиуса, диаметра, периметра и площади окружности для различных значений.

Что такое круг?

Круг — это геометрическая фигура, которая образуется на плоскости при вращении точки вокруг определенной оси, которая называется центром. Линия, которую описывает точка при вращении, называется окружностью. Окружность состоит из всех точек, которые находятся на одинаковом расстоянии от центра.

Одной из основных характеристик круга является его радиус. Радиус — это расстояние от центра круга до любой его точки. Другая основная характеристика круга — диаметр. Диаметр — это отрезок, который соединяет две противоположные точки на окружности и проходит через центр.

Также важным понятием в теории круга является площадь. Площадь круга вычисляется по формуле S = π * r^2, где π — приближенное значение математической константы, равное примерно 3.14, а r — радиус круга.

Круг можно представить с помощью таблицы, где будут указаны его основные характеристики: радиус, диаметр, площадь. Используя эту таблицу, можно легко вычислить значение радиуса или площади круга, если известны другие характеристики.

Правило встречается в следующих упражнениях:

7 класс

Задание 20,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 634,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 660,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 670,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 693,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 11,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1114,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1119,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1290,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1303,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Доказательство теоремы

Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.

Смотри, вот так:

Давай наберёмся мужества и докажем эту теорему.

Если ты читал уже тему «Биссектриса» разбирался в том, почему же три биссектрисы пересекаются в одной точке, то тебе будет легче, но и если не читал – не переживай: сейчас во всём разберёмся.

Доказательство будем проводить, используя понятие геометрического места точек (ГМТ).

Геометрическое место точек, обладающих свойством «\( \displaystyle X\)» — такое множество точек, что все они обладают свойством «\( \displaystyle X\)» и никакие другие точки этим свойством не обладают.

Ну вот, например, является ли множество мячей – «геометрическим местом» круглых предметов? Нет, конечно, потому что бывают круглые …арбузы.

А является ли множество людей, «геометрическим местом», умеющих говорить? Тоже нет, потому что есть младенцы, которые говорить не умеют.

В жизни вообще сложно найти пример настоящего «геометрического места точек». В геометрии проще. Вот, к примеру, как раз то, что нам нужно:

Тут множество – это серединный перпендикуляр, а свойство «\( \displaystyle X\)» — это «быть равноудаленной (точкой) от концов отрезка».

Проверим? Итак, нужно удостовериться в двух вещах:

• Всякая точка на серединном перпендикуляре находится на одинаковом расстоянии от концов отрезка
• Всякая точка, которая равноудалена от концов отрезка – находится на серединном перпендикуляре к ему

Приступим:

Проверим 1. Пусть точка \( \displaystyle M\) лежит на серединном перпендикуляре к отрезку \( \displaystyle AB\).

Соединим \( \displaystyle M\) с \( \displaystyle A\) и с \( \displaystyle B\).Тогда линия \( \displaystyle MK\) является медианой и высотой в \( \displaystyle \Delta AMB\).

Значит, \( \displaystyle \Delta AMB\) – равнобедренный, \( \displaystyle MA=MB\) – убедились, что любая точка \( \displaystyle M\), лежащая на серединном перпендикуляре, одинаково удалена от точек \( \displaystyle A\) и \( \displaystyle B\).

Теперь 2. Почти точно так же, но в другую сторону. Пусть точка \( \displaystyle M\) равноудалена от точек \( \displaystyle A\) и \( \displaystyle B\), то есть \( \displaystyle MA=MB\).

Возьмём \( \displaystyle K\) – середину \( \displaystyle AB\) и соединим \( \displaystyle M\) и \( \displaystyle K\). Получилась медиана \( \displaystyle MK\). Но \( \displaystyle \Delta AMB\) – равнобедренный по условию \( \displaystyle (MA=MB)\Rightarrow MK\) не только медиана, но и высота, то есть – серединный перпендикуляр. Значит, точка \( \displaystyle M\) — точно лежит на серединном перпендикуляре.

Всё! Полностью проверили тот факт, что серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов отрезка.

Это все хорошо, но не забыли ли мы об описанной окружности? Вовсе нет, мы как раз подготовили себе «плацдарм для нападения».

Рассмотрим треугольник \( \displaystyle ABC\). Проведём два серединных перпендикуляра \( \displaystyle {{a}_{1}}\) и \( \displaystyle {{a}_{2}}\), скажем, к отрезкам \( \displaystyle AB\) и \( \displaystyle BC\). Они пересекутся в какой-то точке, которую мы назовем \( \displaystyle O\).

А теперь, внимание!

Точка \( \displaystyle O\) лежит на серединном перпендикуляре \( \displaystyle {{a}_{1}}\Rightarrow OA=OB\);точка \( \displaystyle O\) лежит на серединном перпендикуляре \( \displaystyle {{a}_{2}}\Rightarrow OB=OC\).И значит, \( \displaystyle OA=OB=OC\) и \( \displaystyle OA=OC\).