Вписанная окружность
Окружность называетсявписанной в многоугольник, если она касается его сторон. Центр вписанной окружности лежит в точке пересечения биссектрис углов многоугольника.
Не во всякий многоугольник можно вписать окружность.
Площадь многоугольника, в который вписана окружность можно найти по формуле
,
здесь — полупериметр многоугольника, — радиус вписанной окружности.
Отсюда радиус вписанной окружности равен
Если в выпуклый четырехугольник вписана окружность, то суммы длин противоположных сторон равны. Обратно: если в выпуклом четырехугольнике суммы длин противоположных сторон равны, то в четырехугольник можно вписать окружность:

В любой треугольник можно вписать окружность, притом только одну. Центр вписанной окружности лежит в точке пересечения биссектрис внутренних углов треугольника.
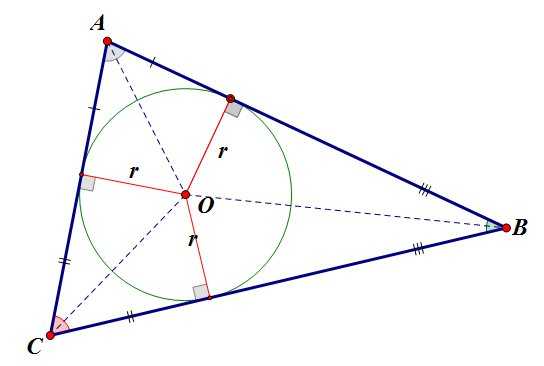
Радиус вписанной окружности равен
. Здесь
Примеры решения задач
Задача 1
Необходимо рассчитать, какова длина окружности, если ее диаметр составляет 5 см.
Решение
При известном диаметре окружности можно рассчитать ее длину с помощью формулы:
\(L = \pi D\)
Подставив известные из условия задачи значения, получим:
\(L = \pi D = 3,14 * 5 = 15,7\) (см)
Ответ: длина окружности равна 15,7 см.
Задача 2
Требуется определить длину окружности, описанной вокруг правильного треугольника, сторона которого составляет \(a=4\sqrt{3}\) дм.
Решение
Радиус окружности составляет:
\(R=\frac{a}{\sqrt{3}}\)
При подстановке переменных формула будет изменена:
\(R=\frac{4\sqrt{3}}{\sqrt{3}}\)
При известном радиусе окружности можно рассчитать длину рассматриваемой окружности, используя соответствующую формулу:
\(L = 2 \pi r=2 \pi *4=2*3,14*4=25,12\) (дм)
Ответ: длина окружности составляет 25,12 дм.
Задача 3
Дана окружность, радиус которой равен 2 см. Требуется рассчитать длину окружности.
Решение
\(L = \pi d\)
d=2 *r= 4
L = 3.14 * 4 = 12,56 (см)
Ответ: длина окружности равна 12,56 см.
Задача 4
Имеется окружность с радиусом 3 см. Необходимо определить длину данной окружности.
Решение
\(L = \pi d\)
L = 3.14 * 3 = 9,42 (см)
Как найти периметр окружности
Существуют разные формулы для вычисления периметра окружности. Целесообразность применения в процессе решения задач того или иного справедливого соотношения параметров круга зависит от исходных условий. К примеру, рассчитать, чему равна длина окружности при известном радиусе можно с помощью такого уравнения:
\(P=2\pi r\)
В данном случае, \(\pi\) является постоянной величиной, которую при расчете округляют до значения 3,14, r обозначает радиус окружности.
Другой способ вычисления периметра круга заключается в применении следующей формулы с учетом значения радиуса:
\(P=\pi d\)
В данном случае, \(\pi\) является постоянной величиной, которую при расчете округляют до значения 3,14, d обозначает диаметр окружности.
Длина окружности (периметр круга)
Будем выводить длину произвольной окружности \(C \)
с помощью её радиуса, равного \(τ \)
.
Будем рассматривать две произвольные окружности. Обозначим их длины через \(C \)
и \(C» \)
, у которых радиусы равняются \(τ \)
и \(τ» \)
. Будем вписывать в эти окружности правильные \(n \)
-угольники, периметры которых равняются \(ρ \)
и \(ρ» \)
, длины сторон которых равняются \(α \)
и \(α» \)
, соответственно. Как мы знаем, сторона вписанного в окружность правильного \(n \)
– угольника равняется
\(α=2τsin\frac{180^0}{n} \)
Тогда, будем получать, что
\(ρ=nα=2nτ\frac{sin180^0}{n} \)
\(ρ»=nα»=2nτ»\frac{sin180^0}{n} \)
\(\frac{ρ}{ρ»}=\frac{2nτsin\frac{180^0}{n}}{2nτ»\frac{sin180^0}{n}}=\frac{2τ}{2τ»} \)
Получаем, что отношение \(\frac{ρ}{ρ»}=\frac{2τ}{2τ»} \)
будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть
\(\lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{2τ}{2τ»} \)
С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть \(n→∞ \)
), будем получать равенство:
\(lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{C}{C»} \)
Из последних двух равенств получим, что
\(\frac{C}{C»}=\frac{2τ}{2τ»} \)
\(\frac{C}{2τ}=\frac{C»}{2τ»} \)
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
\(\frac{C}{2τ}=const \)
Эту постоянную принять называть числом «пи» и обозначать \(π \)
. Приближенно, это число будет равняться \(3,14 \)
(точного значения этого числа нет, так как оно является иррациональным числом). Таким образом
\(\frac{C}{2τ}=π \)
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
\(C=2πτ \)
В вашем браузере отключен Javascript. Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Узнать длину окружности
Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Рассчитать площадь шара
Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Вычислить объем шара
Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы
, понятия и определения требуются для этого.
Длина окружности
Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в 3,14 раза. Для обозначения этой величины используется маленькая (строчная) греческая буква π (пи):
| C | = π. |
| D |
Таким образом, длину окружности (C) можно вычислить, умножив константу π на диаметр (D), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
где C — длина окружности, π — константа, D — диаметр окружности, R — радиус окружности.
Так как окружность является границей круга, то длину окружности можно также назвать длиной круга или периметром круга.
Площадь кольца и других сложных фигур
Если какая-либо фигура образована с помощью нескольких окружностей, то найти ее площадь можно, представив ее в виде суммы площадей нескольких более простых фигур. В качестве простейшего примера можно привести кольцо. По сути оно представляет собой круг, в котором есть круговое отверстие:

Если обозначить наружный радиус кольца буквой R, а радиус отверстия буквой r, то площадь кольца можно найти, вычтя из площади большего круга площадь отверстия:
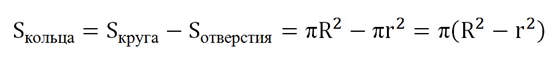
Задание. Внешний радиус кольца составляет 20 см, а радиус отверстия в нем равен 15 см. Определите площадь кольца.
Решение. Подставляем числа в формулу:
![]()
Ответ: 175π.
Задание. Есть диск радиусом 1 метр. Необходимо вырезать в нем отверстие так, чтобы масса диска уменьшилась в два раза. Какой радиус должен быть у отверстия?
Решение. Можно считать, что масса диска пропорциональна его площади, поэтому нам надо, чтобы площадь диска уменьшилась вдвое. Начальная площадь диска определяется так:
Площадь кольца должна быть вдвое меньше, то есть она будет составлять π/2. Если радиус отверстия мы обозначим как r, то можно составить уравнение:

Ответ: ≈ 70,7 см.
В прямоугольной плите с габаритами 180 и 60 см сделано 27 отверстий диаметром 10 см. Вычислите площадь этой плиты. Считайте, что π ≈ 3,1416, и округлите ответ до целых.

Решение. Надо найти площадь плиты без учета отверстий, а потом вычесть из нее площадь всех отверстий. Площадь плиты равна произведению ее сторон

Ответ: ≈ 8679 см2.
Задание. Из вершин квадрата со стороной а проведены дуги радиусом а/2. В результате получили следующую фигуру:
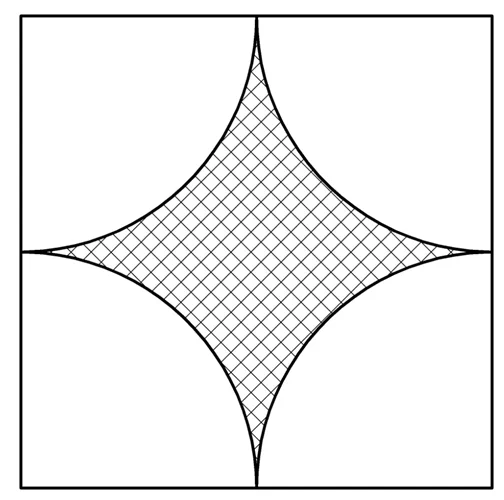
Найдите заштрихованную площадь.
Решение. Площадь заштрихованной области может быть получена, если из площади квадрата мы вычтем площади 4 секторов. Площадь квадрата рассчитывается так:

Задание. В квадрате, сторона которого обозначается буквой а, из вершин провели дуги, чей радиус совпадает со стороной квадрата. В результате в центре квадрата получили следующую фигуру:
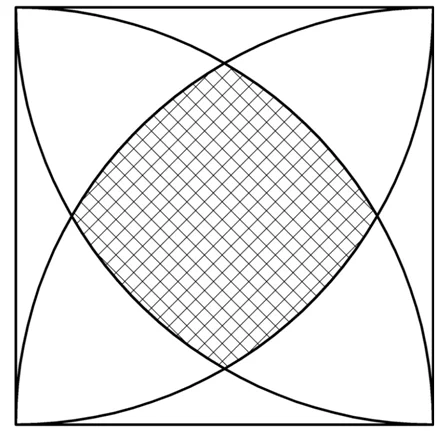
Определите, какую долю квадрата занимает эта центральная фигура. Ответ дайте в процентах и округлите его до десятых.
Решение. Задача решается в несколько действий, причем нам потребуется составить формулы для вычисления площадей вспомогательных фигур. Сначала найдем площадь маленького треугольника с «кривыми» сторонами, для чего используем такое построение:
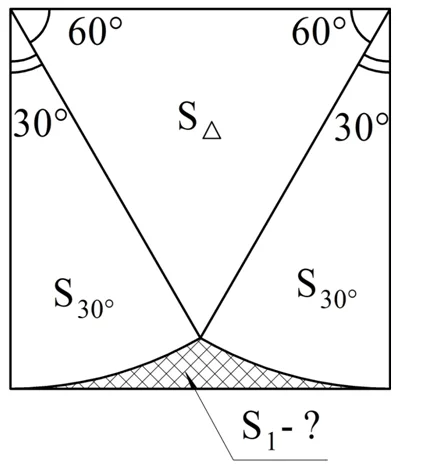
Площадь, которую мы пытаемся найти, обозначена здесь как S1. Ее можно получить, просто вычтя из площади квадрата (она составляет а2) площади двух секторов и площадь треугольника. Треугольник на рисунке – равносторонний, ведь и сторона квадрата, и радиусы окружностей равны величине а. Тогда каждый его угол составляет 60°, и его площадь можно найти так:

Также мы можем найти центральные углы обоих секторов. Так как углы в квадраты составляют 90°, а в равностороннем треугольнике 60°, то эти углы окажутся равными 90° – 60° = 30°. Тогда площадь сектора вычисляется по формуле:

На следующем шаге вычислим площадь другой фигуры:

Попытаемся выразить величину S2. Для этого из площади квадрата надо вычесть площадь сектора, у которого центральный угол составляет 90°. Найдем площадь этого сектора:

Здесь мы ищем площадь S3
Обратите внимание, что ее можно выразить через уже найденные нами величины S1 и S2:

Мы составили выражения для всех необходимых нам вспомогательных фигур. Теперь вернемся к исходному рисунке и отметим на нем эти вспомогательные фигуры:
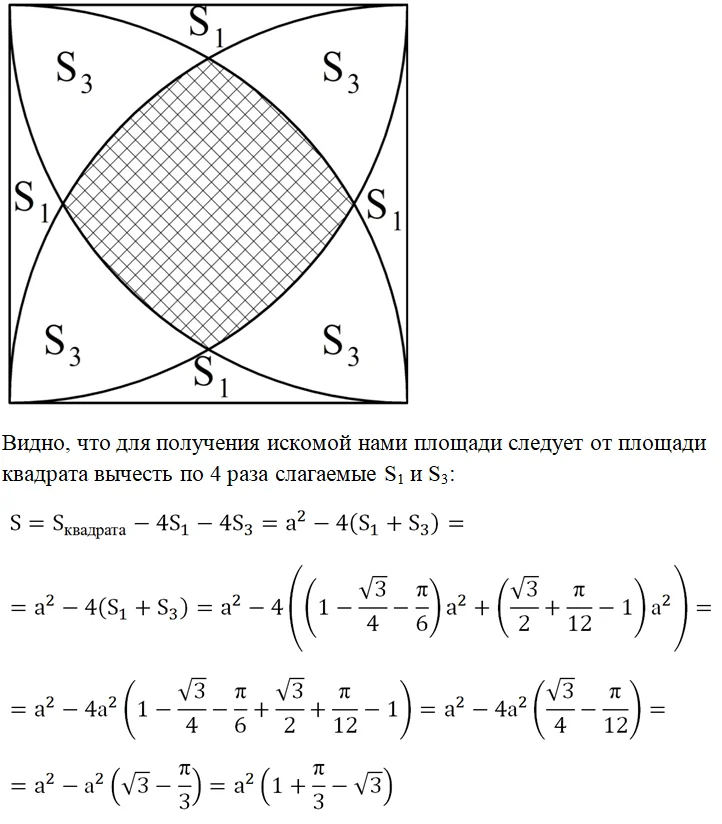
Итак, мы составили выражение для вычисления площади центральной фигуры. По условию надо указать, сколько процентов она составляет от площади всего квадрата. Для ответа на этот вопрос поделим площадь фигуры на площадь квадрата и умножив это отношение на 100%:
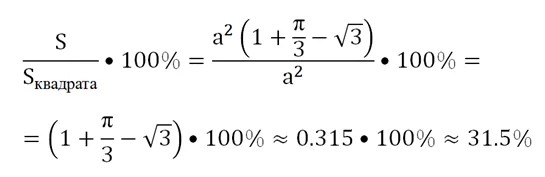
Ответ: 31,5%.
В рамках этого урока мы узнали, как вычислять длину окружности и дуги, площади круга, сектора, сегмента, кольца и других фигур, одна или несколько сторон которых представляют собой дуги окружности. Эти навыки могут пригодиться и в реальной жизни, так как именно от площади многих предметов часто зависит потребность в краске, лаке, клее и т. п.
Что такое длина окружности?
После того как мы рассмотрели все определения, мы можем высчитывать диаметр окружности. Формула будет рассмотрена немного позже.

Для начала мы попробуем измерить длину очертания стакана. Для этого мы обмотаем его ниткой, затем ее измерим линейкой и узнаем приблизительную длину воображаемой линии вокруг стакана. Потому что размер зависит от правильного измерения предмета, а данный способ не является надежным. Но тем не менее сделать точные измерения вполне возможно.
Для этого опять вспомним о колесе. Неоднократно мы видели, что если увеличить спицу в колесе (радиус), то увеличится и длина обода колеса (окружности). И так же при уменьшении радиуса окружности уменьшается и длина обода.
Если внимательно проследить за этими изменениями, то увидим, что длина воображаемой круглой линии пропорциональна ее радиусу. И данное число является постоянным. Дальше рассмотрим, как определяется диаметр окружности: формула для этого применится в примере ниже. И рассмотрим ее, следуя шаг за шагом.
Что такое окружность
Окружность представляет собой кривую линию, достаточно распространенную в окружающем нас мире. Ее рассматривают в рамках какой-либо плоскости. Изобразить окружность можно с помощью циркуля или веревки, один конец которой фиксируют в одной точке. В том и другом варианте начертания точки окружности равноудалены от центра.
Некий отрезок, соединяющий центральную точку и такую точку, которая лежит на окружности, принято считать радиусом. Если перевести этот термин с латинского языка, то получится «спица колеса». Данная ассоциация вполне логична, так как, по сути, окружность является математической моделью колеса.
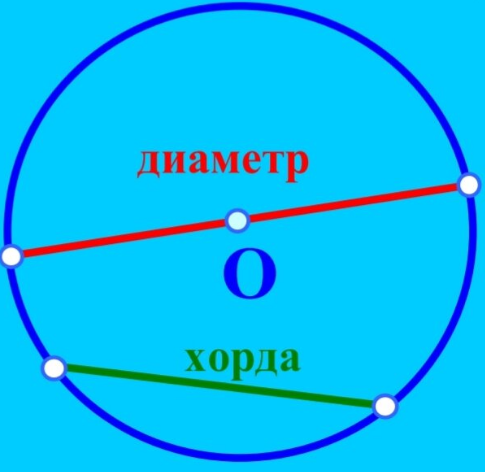
Соединяя пару точек, расположенных на окружности, получают хорду. В греческом языке хорда понимается как «струна». В том случае, когда этот отрезок пересекает центральную точку окружности, его называют диаметром. Протяженность диаметра ровно в два раза больше по сравнению с размером радиуса окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут


Окружностью называют множество точек, расположенных на некой плоскости, которые равноудалены от одной заданной точки.
Радиус окружности представляет собой отрезок с началом, совпадающим с центральной точкой, и концом, расположенным в любой из точек рассматриваемой окружности.
Хорда является отрезком, который соединяет пару каких-либо точек окружности.
Диаметром называют хорду, проходящую через центральную точку окружности.
Число пи
Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Такие калькуляторы легко найти любым поисковиком. Найти номера телефонов проституток Питера теперь легко. В этом поможет богатый каталог шлюх, на сайте. А потому и не стоит растрачивать время зря. Заходи, выбирай, звони. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Формулы круга и окружности
- Формула площади круга
- Формула периметра круга (длины окружности)
Круг — геометрическое место точек плоскости, расстояние от которых до данной точки не больше, чем заданное ненулевое.
Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая. Также круг можно определить как часть плоскости, ограниченную окружностью.
Формула площади круга
Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади круга выражается числом заключающихся в него квадратных единиц.
1) Площадь круга равна произведению квадрата радиуса на число пи (3.1415).
2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.
S — площадь круга
π — число пи (3.1415)
r — радиус круга
Формула периметра круга (длины окружности)
Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.
1) Периметр круга равен произведению радиуса на два пи (3.1415).
P — Периметр круга (длина окружности)
π — число пи (3.1415)
r — радиус круга (окружности)
Основные формулы с пояснением
Обладая информацией о радиусе и диаметре окружности, достаточно просто рассчитать ее длину. Однако не во всех задачах присутствуют эти данные. Есть ряд примеров, в которых определить длину окружности необходимо с помощью параметров другой геометрической фигуры.
Вычисление длины окружности через площадь круга
В том случае, когда известна площадь круга, можно рассчитать длину окружности по формуле:
\(L=\sqrt{S4\pi }\)
где \(\pi\) — является числом пи, значение которого равно 3,14;
S — определяет площадь круга
Расчет длины окружности через диагональ вписанного прямоугольника
В задачах можно встретить примеры вписанного в окружность прямоугольника.

В этом случае длина окружности рассчитывается по формуле:
\(L=\pi * d\)
где \( \pi\) — является числом пи, значение которого равно 3,14;
d — является диагональю рассматриваемого прямоугольника.
Как вычислить длину окружности через сторону описанного квадрата
В том случае, когда окружность вписана в квадрат с прямыми углами, сторона которого известна, можно определить длину этой окружности.
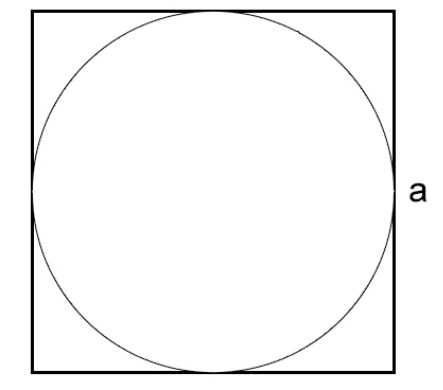
\(L=\pi * a\)
где \(\pi \) — является числом пи, значение которого равно 3,14;
a — определяет длину стороны квадрата
Расчет длины окружности с помощью сторон и площади вписанного треугольника
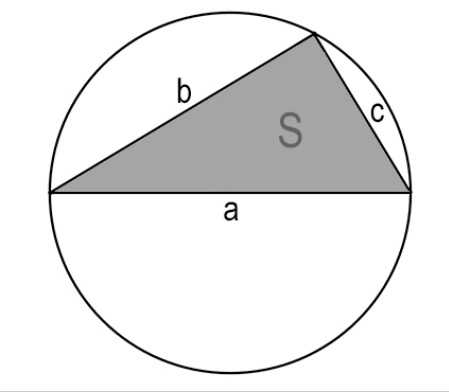
Предположим, что в окружность вписан треугольник. Если имеется информация о всех его трех сторонах, а также площади, то можно рассчитать длину окружности, оперируя следующей формулой:
\(L=\pi *\frac{abc}{2S}\)
где \(\pi\) — математическая константа со значением 3,14;
a — является первой стороной треугольника;
b — является второй стороной треугольника;
с – является третьей стороной треугольника;
S – определяется, как площадь рассматриваемого треугольника.
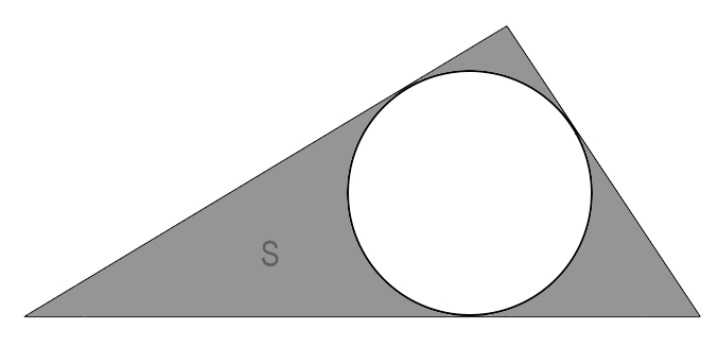
Способ нахождения длины окружности при известной площади и полупериметру описанного треугольника
Представим, что в какой-то треугольник вписана окружность. Известно значение площади треугольники и его полупериметр. Необходимо рассчитать длину окружности. Следует заметить, что периметром треугольника называют сумму всех его сторон, а полупериметр составляет половину этой суммы. Таким образом, для нахождения полупериметра нужно определить периметр треугольника и разделить его на два.
Формула расчета длины окружности:
\(L=2\pi *\frac{S}{p}\)
где \(\pi\) — математическая константа со значением 3,14;
S — является площадью треугольника;
p — представляет собой полупериметр треугольника.
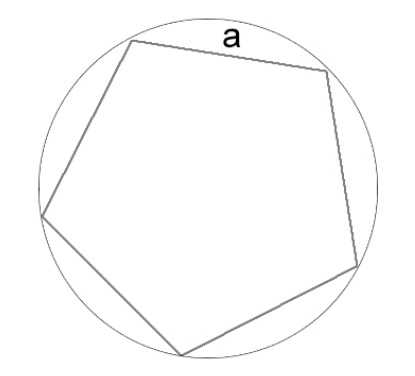
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Когда в окружность вписан правильный многоугольник, в первую очередь стоит сосчитать количество его сторон. Также требуется знать длину стороны этой геометрической фигуры. Стороны правильного многоугольника одинаковы, как у квадрата. В этом случае формула для расчета длины окружности имеет вид:
\(L=\pi *\frac{a}{\sin \frac({180}{N})}\)
где \(\pi\) — математическая константа со значением 3,14;
a — это сторона многоугольника;
N — определяет количество сторон многоугольника.
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
В пределах окружности имеются точки Х такие
, что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
Основные термины окружности
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками
, проходящее через центр фигуры.
Онлайн калькулятор
Для того чтобы рассчитать периметр круга (длину граничной окружности) вам необходимо знать его радиус или диаметр, либо его площадь.
Ликбез: Круг — часть плоскости, лежащая внутри окружности.
Как посчитать периметр круга зная радиус
Чему равен периметр круга если
Каков периметр круга (L) если его радиус r ?
L = 2⋅π⋅r , где π ≈ 3.14
Если радиус круга равен 0.5 см, то его периметр равен числу π, то есть ≈ 3.14 см.
Как посчитать периметр круга зная диаметр
Чему равен периметр круга если
Каков периметр круга (L) если его диаметр d?
L = π⋅d , где π ≈ 3.14
Если диаметр круга d = 1 см, то его периметр равен числу π, то есть ≈ 3.14 см.
Чему равен периметр круга если
Каков периметр круга (L) если его площадь S?
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
∠ОAС = ∠OAB
Примеры решения задач
Задача 1
Имеется некая окружность с радиусом 12 см. Необходимо вычислить, чему равна длина этой окружности.
Решение
Зная, что вычислить длину окружности при известном ее радиусе можно по стандартной формуле, подставим в выражение числовые значения и запишем ответ:
\(C = 2 \cdot 3,14 \cdot 12 = 75,36\)
Ответ: 75,36 см.
Задача 2
Диаметр окружности равен 15 см. Нужно определить периметр круга, который ограничен этой окружностью.
Решение
Периметр круга в данном случае соответствует длине окружности. Вычислить искомую величину можно, зная диаметр окружности:
\(C = 3,14 \cdot 15 = 47,1\)
Ответ: 47,1 см.
Задача 3
Окружность обладает длиной, равной 12. Ее центр обозначен буквой О. Угол \(\angle AOB\) составляет \(120^{\circ}\). С помощью точек А и В, которые принадлежат окружности, она делится на пару дуг. Требуется вычислить, во сколько раз длина максимальной из образованных дуг больше по сравнению с длиной меньшей.
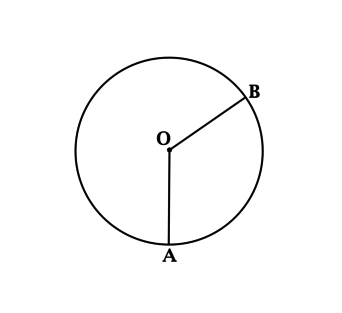
Решение
Известно, что отношение длин дуг соответствует отношению их градусных мер. Зная, что О является центральной точкой окружности, определим \(\angle AOB\), как центральный. Дуга по градусной мере меньше по сравнению с полуокружностью. Ее градусная мера соответствует градусной мере центрального угла, опирающегося на эту дугу. Меньшая дуга равна \(120^{\circ}\), а градусная мера максимальной дуги составляет \(240^{\circ}\). Таким образом:
\(240 \div 120 = 2\)
Ответ: 2.
Задача 4
На рисунке изображена окружность с центральной точкой О. Длина этой окружности составляет 18 см. Сектор АОВ обладает площадью \(\dfrac{18}{\pi}см^2\). Требуется определить, чему равна длина дуги АВ рассматриваемого сектора.
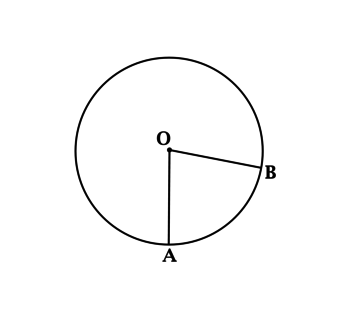
Решение
Запишем формулу для вычисления длины окружности при ее известном радиусе:
\(С = 2\pi R\)
Согласно условию задачи:
\(18 = 2\pi R\)
В таком случае:
\(R = \dfrac{9}{\pi}\)
Площадь сектора, градусная мера дуги которого составляет \(\alpha\), равна:
\(\pi R^2 \cdot \dfrac{\alpha}{360}\)
Тогда запишем выражение для расчета длины дуги с градусной мерой \(\alpha\):
\(2\pi R\cdot \dfrac{\alpha}{360}\)
Если умножить площадь сектора с дугой, равной \(\alpha\), на \(\dfrac{2}{R}\), то получится определить длину дуги с градусной мерой \(\alpha\). В результате длина дуги АВ рассматриваемого сектора составляет:
\(\dfrac{18}{\pi} \cdot \dfrac{2\pi}{9} = 4\)
Ответ: 4 см.
Задача 5
На рисунке изображено пересечение пары окружностей. Требуется вычислить длину внешней границы фигуры, которая получилась в результате. Длина окружности составляет 12.
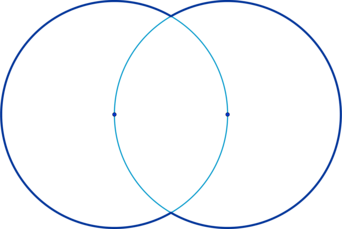
Решение
Проведем отрезок через центральные точки окружностей. Соединим центры этих фигур с точками, в которых окружности взаимно пересекаются. Заметим, что можно сформировать пару равносторонних треугольников со сторонами, равными радиусам рассматриваемых окружностей.
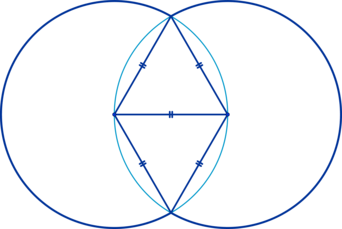
Дуга, принадлежащая одной окружности, которая находится внутри сформированной фигуры, имеет опору в виде угла. Этот угол равен паре углов, принадлежащих равностороннему треугольнику, и составляет \(120^\circ\). Таким образом, длину этой дуги допустимо вычислить по следующей формуле:
\(\frac{C_{120^\circ}}{12} = \frac{120^\circ}{360^\circ} \Rightarrow C_{120^\circ} = 4\)
В результате длина внешней границы при пересечении окружностей составляет:
\(L = 2\cdot C — 2\cdot C_{120^\circ} = 2\cdot12 — 2\cdot 4 = 16\)
Ответ: 16.
Задача 6
На рисунке изображена окружность с некоторыми известными величинами. Требуется рассчитать меру \(\angle AOB\).

Решение
Запишем, чему равна общая длина окружности:
С = 1 + 2 + 5 + 10 = 18
В таком случае упрощается нахождение искомого угла:
\(\frac{C_{\angle AOB}}{C} = \frac{\angle AOB}{360^\circ} \Rightarrow \frac{5}{18} = \frac{\angle AOB}{360^\circ} \Rightarrow \angle AOB = 100^\circ\)
Практическое применение
Формула длины окружности 2πr имеет широкое практическое применение в различных областях науки, техники и повседневной жизни. Например:
- Расчет длины провода для обмотки электромотора.
- Вычисление длины трубы для газопровода или водопровода, чтобы определить необходимое количество материала.
- Рассчёт периметра колеса велосипеда или автомобиля, который используется при измерении скорости и расстояния.
- Определение длины браслета или ожерелья, используя диаметр круглых бусин.
- Расчет длины ленты для изготовления декоративных украшений.
- Измерение длины проволоки, которая используется для создания каркаса строительных конструкций.
- Рассчёт количества обоймы для двуствольного оружия, зная длину каждой.
Без формулы длины окружности, измерение длины круга становится крайне сложной задачей.
Эта формула также является основой для других математических формул, таких как формула для нахождения площади круга S = πr^2 и объема шара V = (4/3)πr^3.































