Как найти площадь сектора круга

Примеры расчета площади круга

Площадь круга играет важную роль в повседневной жизни. Рассмотрим несколько интересных примеров:

1. Представьте, что у вас есть круглый бассейн диаметром 10 метров. Сколько воды он может вместить? Начнем с расчета площади: S = π * (10/2)² = 78.54 м². Теперь вы знаете, что поверхность вашего бассейна составляет 78.54 м².

2. Шляпа-сомбреро для пляжного отдыха! Если радиус вашей шляпы равен 35 см, то какова ее площадь? S = π * 35² = 3848.45 см². Это впечатляющая площадь для шляпы!

3. Представьте круглую пиццу диаметром 30 см. Какова площадь этой пиццы? Именно столько сыра и томатного соуса понадобится пиццерии. S = π * (30/2)² = 706.86 см². Очень аппетитно!

Площадь сегмента круга по хорде и высоте

Пусть градусная мера ограничивающей дуги мала, длина хорды равна a, h — высота сегмента (перпендикуляр, опущенный из точки на окружности к середине хорды). Примечание: часто высота сегмента называется «стрелкой».

Тогда можно приближённо считать, что

Погрешность такого вычисления уменьшается вместе с отношением

В частности, когда дуга содержит угол, меньший 50º, то есть, 

погрешность оказывается менее 1%.

Более точной является формула для любого сегмента меньшего полукруга:

Точный расчёт производится, исходя из свойства нахождения сложной фигуры, являющейся суммой или разностью двух и более объектов.

Сегмент является частью сектора, к которому либо добавлен треугольник, содержащий центральный угол (для дуг больших 180º), либо убран (соответствующий центральный угол меньше 180º).

Отсюда следует, что

Задача №5

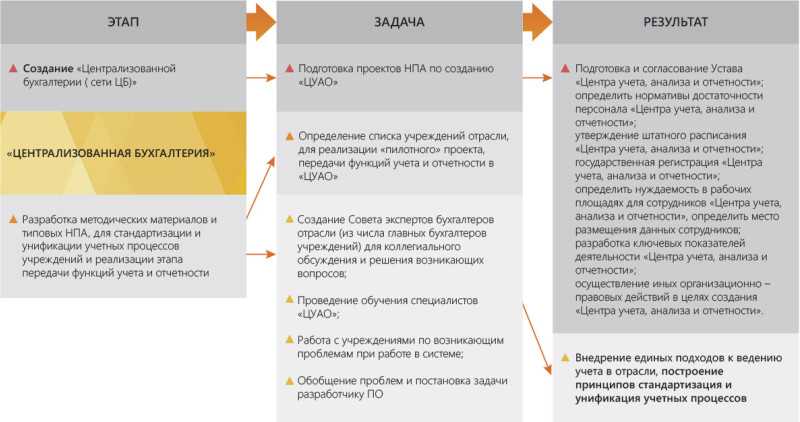
Вычислить стрелку и площадь сегмента, если центральный угол содержит 60º, а 

Решение.

Для нахождения стрелки достаточно из радиуса вычесть высоту треугольника AOB. Поскольку угол AOB по условию равен 60º, то треугольник AOB равносторонний. Поэтому его высота в √3/2 раз отличается от стороны (от радиуса). 

Отсюда следует, что:

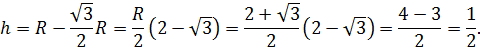
Площадь по первой формуле будет приблизительно равна

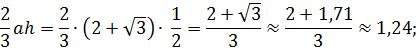
По второй:

Применяя точную формулу и учитывая, что

находим:

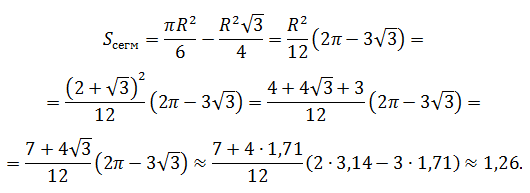
Ответ: S_сегм = 1,26 см2.

Основные преимущества мониторинга обменников BestChange

• Один из самых первых и проверенных временем мониторингов электронных обменников, работающий с 2007 года.
• В базе мониторинга более 400 онлайн обмеников.
• БестЧендж посещает несколько десятков тысяч пользователей ежедневно, что говорит о высоком доверии к нему.
• Для сравнения курса обмена в мониторинге можно выбрать десятки наиболее популярных направлений обмена: платежные системы (QIWI, Advanced Cash, Payeer, Perfect Money, WebMoney, Яндекс Деньги и т.д.), криптовалюты (Bitcoin, Ethereum, Ripple, Monero, Waves и т.д.), онлайн-банкинги (Сбербанк Онлайн, Приват24, Альфа Банк, Тинькофф, Бинбанк и т.д.), системы денежные переводов (Western Ubion, Money Gram, Contact, Золотая Корона и т.д.), а также наличные деньги (РФ, Украина).
• Обновление данных по реальному курсу обмена, отзывам и резерву в обменниках проходят каждые 5-10 секунд.
• Для удобства работы пользователей есть расширение BestChange для браузеров.
• Можно посмотреть статистику изменения курса в выбранном направлении обмена за определенный период времени.
• Пользователям доступна возможность подписываться на уведомления, когда в обменниках по выбранному направлению появиться нужный резерв средств или курс обмена станет более выгодным.
• Для постоянных пользователей мониторинга BestChange есть система ежедневных бонусов и выгодная партнерская программа.

Зачем иметь дело с областями секторов?

Сектора тесно связаны с углами в

градусы и радианы

и очень часто с ними приходится иметь дело в геометрии, и с ними связано несколько интересных математических результатов.

Идея о том, что площадь секторов связана с размером кусочка пиццы, должна быть достаточной, чтобы заинтересоваться, да?

Пример: площадь сектора

Найдите площадь сектора, соответствующего углу \(\alpha = \pi\) радиан, с радиусом r = 3.

Отвечать:

Нам нужно найти площадь сектора. У нас есть информация, что радиус равен \(r = 3\), а сектор задан углом \(\alpha = \pi\) радиан.

Пусть \(A\) — площадь соответствующего сектора, а \(r\) — радиус круга. Мы имеем следующую прямую пропорцию:

Эта прямая пропорция показывает, что площадь сектора \(A\) прямо пропорциональна углу сектора. Мы можем решить для \(A\), и получим

Теперь осталось только подставить известные значения радиуса и угла, и мы получим:

На этом вычисления завершены. Мы выяснили, что площадь соответствующего сектора круга равна \(\displaystyle A = \frac{9}{2}\pi{}\).

Пример: вычисление площади сектора

Теперь вычислите площадь сектора для круга с радиусом r = 2 и углом сектора \(\alpha = 45\) градусов

Отвечать:

Нам нужно найти площадь сектора. У нас есть информация, что радиус равен \(r = 2\), а сектор задан углом \(\alpha = 45\) градусов. Поэтому в данном случае угол задан в градусах.

Пусть \(A\) — площадь соответствующего сектора, а \(r\) — радиус круга. Мы имеем следующую прямую пропорцию:

Эта прямая пропорция показывает, что площадь сектора \(A\) прямо пропорциональна углу сектора. Мы можем решить для \(A\), и получим

Теперь осталось только подставить известные значения радиуса и угла, и мы получим:

На этом вычисления завершены. Мы выяснили, что площадь соответствующего сектора круга равна \(\displaystyle A = \frac{1}{2}\pi{}\).

Пример: другой расчет

Какова площадь сектора, если угол равен \(2\pi\) радиан.

Отвечать:

В данном случае \(2\pi\) радиан соответствует полному кругу, поэтому площадь равна площади круга, \(A = \pi r^2\).

Онлайн-калькулятор для расчета длины дуги кругового сектора

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

В публикации представлены онлайн-калькуляторы и формулы, с помощью которых можно рассчитать длину дуги кругового сектора через радиус окружности и центральный угол сектора (в градусах или радианах).

• Расчет длины дуги сектора
  • Через радиус круга и угол сектора в градусах
  • Через радиус круга и угол сектора в радианах

Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина с учетом указанных данных.

Напомним, дуга кругового сектора – это участок между двумя точками, лежащими на линии окружности и полученными в результате пересечения этой окружности двумя радиусами, образовавшими сектор круга.

AOBAB

Примечание: число π, используемое в калькуляторе, округлено до 3,1415926536.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Похожие калькуляторы

Вам могут пригодиться следующие калькуляторы на эту же тему:

• Калькулятор площади поверхности шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы) с помощью нашего онлайн-калькулятора.
• Калькулятор площади правильного шестиугольника. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью нашего онлайн-калькулятора.
• Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
• Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
• Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
• Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
• Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в квадратных метрах или литрах.
• Онлайн-калькулятор длины дуги. Найдите длину дуги, используя радиус, угол центрального сектора или формулу Гюйгенса.
• Калькулятор объема трубы. Определите объем трубы в кубических метрах или литрах, просто введя диаметр и длину трубопровода.
• Калькулятор объема пирамиды. Оцените объем пирамиды, используя высоту, площадь или сторону её основания. Подходит для всех форм оснований.

Расчёт полукруглой теплицы — онлайн калькулятор

Укажите необходимый масштаб чертежей.

Заполните параметры теплицы в миллиметрах:

X – Ширина теплицы выбирается исходя из бюджета, наличия свободного места для размещения на участке, а также Ваших пожеланий и целей. Стандартная ширина теплиц заводского изготовления находится в пределах 1800-6000 мм. Оптимальное значение X для комфортной работы в теплице не меньше 2400 мм. Такой размер позволяет оборудовать в теплице проход шириной 600 мм (что оптимально), поставить стеллажи с рассадой или оборудовать грядки по обе стороны до 900 мм (сложно ухаживать за растениями дотягиваясь дальше указанного расстояния).

Z – Длина парника, может быть любой, если позволяют размеры участка.  При выборе значения Z следует учитывать стандартные размеры материала, который будет применяться для остекления. Например, если используется полиэтиленовая пленка значение длины Z должно быть кратным 1000 мм, а если поликарбонат – кратным 2100 мм.

Один из решающих аспектов, влияющих на выбор ширины и длины теплицы, это ширина покрытия.

Y – Высота теплицы выбирается исходя из удобства работы в ней (определяющим фактором является рост работника). Значение Y влияет на длину дуги каркаса (больше высота – длиннее дуга и большее количество материала необходимо для остекления). Оптимальная высота теплицы 2000 – 2200 мм.

При выборе основных параметров теплицы следует учитывать рекомендации СП 107.13330.2012 «Теплицы и парники» (актуализированная редакция СНиП 2.10.04-85).

A – Количество вертикальных секций на фасаде теплицы, следует выбирать с учетом геометрических размеров материала для обшивки.

E – Число вертикальных сегментов стен, зависит от размеров используемого для обшивки материала и длины парника. Например, для шести метровой теплицы остекленной поликарбонатом стандартной ширины, значение E следует принимать не меньше 3.

D – Количество ячеек в вертикальном сегменте принимается с учетом свойств материала остекления и прочности каркаса.  Если используется поликарбонат, достаточно значения  D=3 (поскольку в конструкции он согнут и напряжен, то хорошо воспринимает нагрузки на растяжение-сжатие), для парниковой пленки следует принимать значение D больше чтобы исключить провисание.

У Вас есть возможность подобрать оптимальные размеры секций и ячеек изменяя их количество, при этом размеры будут отображены на чертежах теплицы.

Нажмите «Рассчитать»

Калькулятор поможет посчитать площадь, объем и периметр полукруглой теплицы. А также площади крыши, боковых стен и фасадов и полную площадь остекления, что необходимо для закупки материала обшивки в нужном количестве.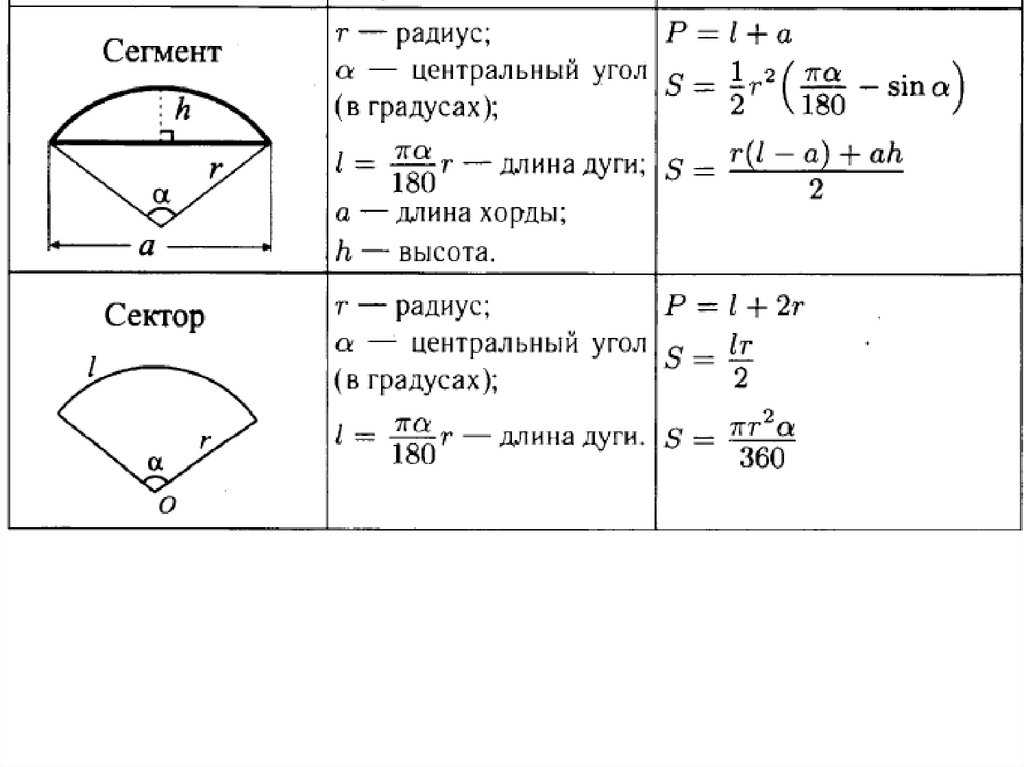

Как использовать формулу площади сектора?

Площадь сектора будет основана на

формула площади круга

при рассмотрении всего круга.

— Во-первых, чтобы дать формулу для площади сектора, нужно различать два случая: угол задан в радианах или угол задан в радианах.

— Предположим, что угол α задан в градусах, и пусть A — площадь соответствующего сектора, а r — радиус. Мы имеем следующую прямую пропорцию:

Эта прямая пропорция говорит о том, что площадь сектора прямо пропорциональна углу. Решив для A, мы получим

— Предположим, что угол α задан в радианах, и пусть A — площадь соответствующего сектора, а r — радиус. Теперь мы имеем следующую прямую пропорцию:

Эта прямая пропорция говорит о том, что площадь сектора прямо пропорциональна углу. Решив для A, мы получим

Как рассчитать длину хорды, образованной углом

Длину хорды можно рассчитать с помощью правила косинуса.

Для треугольника XYZ на схеме ниже сторона, противоположная углу θ, представляет собой хорду длиной c.

Из правила косинуса:

Упрощение:

или c 2 = 2 R 2 (1 — cos θ )

Но из формулы половинного угла (1- cos θ ) / 2 = sin 2 ( θ / 2) или (1- cos θ ) = 2sin 2 ( θ / 2)

Подстановка дает:

c 2 = 2 R 2 (1 — cos θ ) = 2 R 2 2sin 2 ( θ / 2) = 4 R 2 sin 2 ( θ / 2)

Извлечение квадратного корня из обеих сторон дает:

с = 2 R sin ( θ / 2)

Более простой вывод, полученный путем разделения треугольника XYZ на 2 равных треугольника и использования синусоидального соотношения между противоположной стороной и гипотенузой, показан в вычислении площади сегмента ниже.

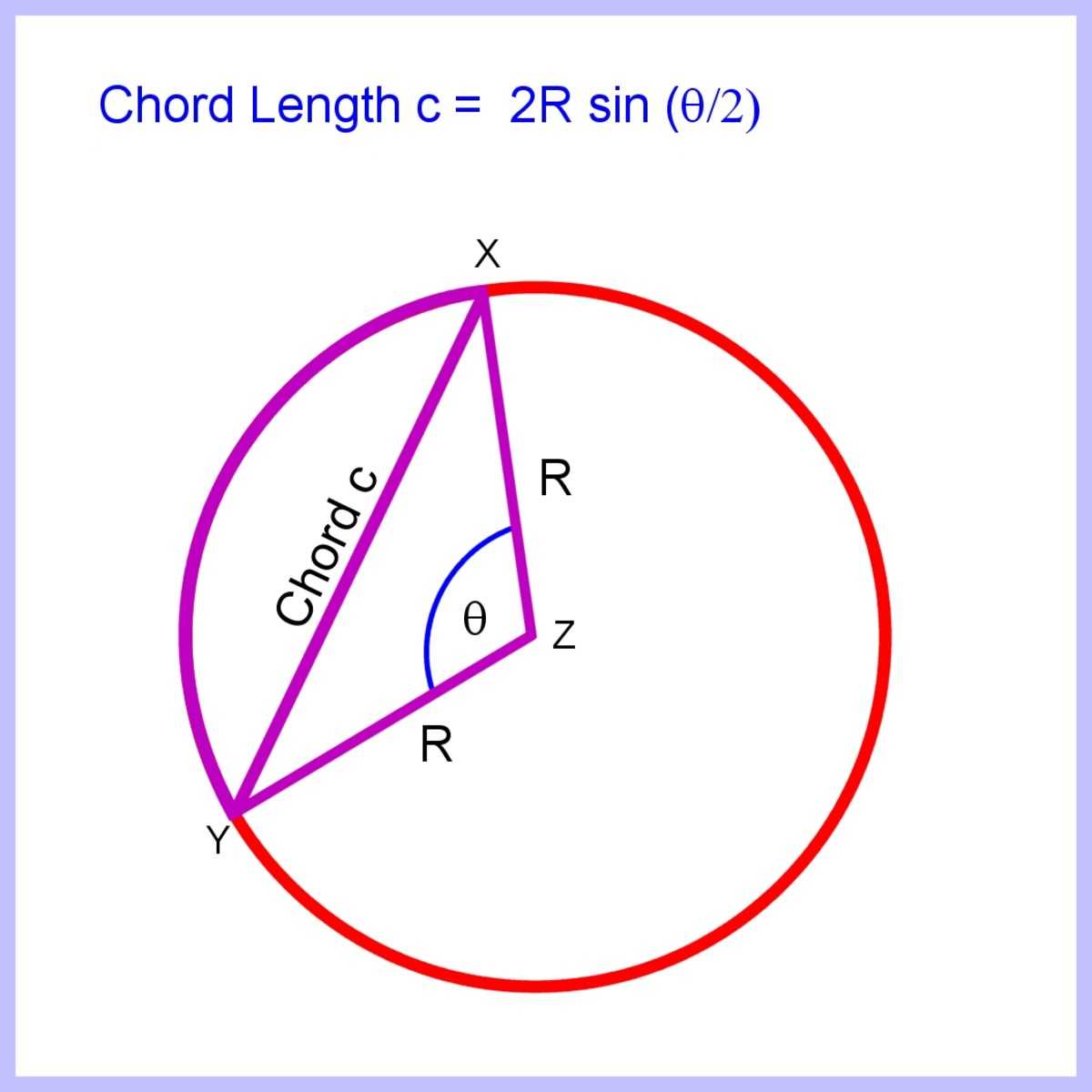
Длина хорды

Изображение Юджин Бреннан

Площадь сектора круга через радиус и длину дуги

Пусть известны радиус круга R, длина дуги l. Как в этом случае определить площадь сектора, стягиваемого данной дугой?

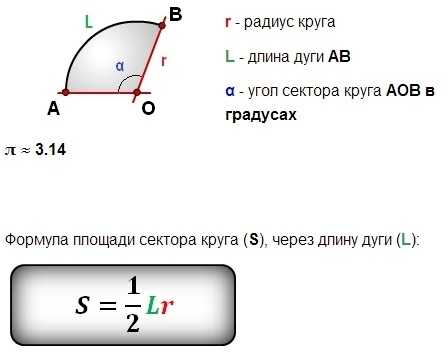
Для ответа на вопрос понадобится формула нахождения длины окружности:

C = 2πR.

Определение, представленное через третью формулировку, даёт возможность соотнести численные величины понятий: сектор и круг, дуга и окружность, центральный и полный углы.

Поскольку отношения постоянны, то для ответа на поставленный вопрос достаточно найти отношение части к целому, затем умножить полученный результат на площадь круга S = πR2.

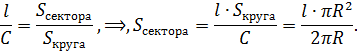
После сокращения дроби получают формулу:

Онлайн калькулятор

По углу и радиусу

Угол α = °радРадиус r = ммсмдммПлощадь сегмента круга S_ск =
мм²см²дм²м²Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*Округление числа π: 3.143.1415915 знаков

По длине хорды и высоте сегмента

Хорда c = ммсмдммВысота сегмента h = ммсмдммПлощадь сегмента круга S_ск =
мм²см²дм²м²Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*

По высоте и радиусу (или диаметру)

Радиус rДиаметр d = ммсмдммВысота сегмента h = ммсмдммПлощадь сегмента круга S_ск =
мм²см²дм²м²Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*

Просто введите данные и получите ответ.

Нюансы расчета площади круга

При расчете площади круга следует учитывать ряд нюансов:

1. Точность значения числа π. В большинстве случаев π приближенно равно 3.14, но для более точных расчетов лучше использовать более длинное значение.

2. Округление результатов. Для большинства повседневных задач округление до двух десятичных знаков будет достаточным.

3. Учет толщины линии при измерении диаметра или радиуса. В некоторых случаях это может повлиять на итоговый результат.

4. Влияние измерительных ошибок. Даже маленькая ошибка в измерении радиуса может значительно повлиять на итоговую площадь.

5. Помните, что результаты в разных единицах измерения (метры, сантиметры, миллиметры) требуют пересчета, если нужно сравнить или комбинировать их.

6. Убедитесь, что используете правильные формулы при комбинировании различных геометрических фигур.

7. Помните о возможных искажениях при визуализации круга на плоскости. На практике идеальные круги редки.

Калькулятор разницы в процентах — Онлайн калькулятор разницы в процентах

Калькулятор разницы в процентах — это онлайн-инструмент, который помогает рассчитать процентную разницу любых двух чисел. Абсолютная величина отношения разности двух чисел к их среднему, выраженная в процентах, называется процентной разницей.

Что такое калькулятор процентной разницы?

Калькулятор процентной разницы поможет вам рассчитать относительную разницу между двумя числами и выразить результат в процентах.

Калькулятор процентной разницы

Калькулятор процентной разницы

Как пользоваться калькулятором процентной разницы?

Пожалуйста, следуйте инструкциям ниже, чтобы найти процентную разницу с помощью калькулятора процентной разницы:

• Шаг 1 : Используйте онлайн-калькулятор процентной разницы Cuemath.
• Шаг 2: Введите начальное значение и конечное значение в поля ввода.
• Шаг 3 : Нажмите « Вычислить », чтобы найти разницу в процентах.
• Шаг 4 : Нажмите « Сброс », чтобы очистить поля и ввести новые значения.

Как работает калькулятор процентной разницы?

Предположим, что заданы начальное и конечное значения величины.

1. Вычтите конечное значение из начального значения.
2. Взять среднее из двух значений. Среднее значение можно рассчитать как сумму наблюдений, деленную на общее количество наблюдений.
3. Разделите разницу, полученную на шаге 1, на среднее значение, полученное на шаге 2.
4. Затем мы берем абсолютное значение числа, полученного на шаге 3. Получение абсолютного значения числа подразумевает, что мы удаляем отрицательный знак числа. Таким образом, абсолютное значение всегда будет положительной величиной. Абсолютное значение величины, скажем, x, представляется как |x|.
5. Значение, полученное на шаге 4, затем умножается на 100, чтобы получить результат в процентах.

Формула для процентной разницы приведена ниже:

Процентная разница = \(\left | \frac{Начальное значение — Конечное значение}{\frac{Начальное значение + Конечное значение}{2}} \right |\times 100\)

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы.

Записаться на бесплатный пробный урок

Решенные примеры на калькуляторе процентной разницы

Пример 1:

Найдите процентную разницу, если заданы значения 100 и 200. Проверьте это с помощью онлайн-калькулятора процентной разницы.

Решение:

Дано: Начальное значение (a) = 100, конечное значение (b) = 200

Разница в процентах = |Разница / Среднее| × 100%

= |(a − b) / ((a + b)/2)| × 100%

= |(100 — 200) / ((100 + 200)/2)| × 100%

= |-100/150| × 100%

= |-0,666| × 100%

= 0,666 × 100%

= 66,666%

Таким образом, процентная разница двух значений = 66,666%.

Пример 2:

Найдите процентную разницу, если заданы значения 300 и 148. Проверьте ее с помощью онлайн-калькулятора процентной разницы.

Решение:

Дано: Начальное значение (a) = 300, конечное значение (b) = 148

Разница в процентах = |Разница / Среднее| × 100%

= |(a − b) / ((a + b)/2)| × 100%

= |(300 — 148) / ((300 + 148)/2)| × 100%

= |152 / 224| × 100%

= 0,678 × 100%

= 67,8%

Таким образом, процентная разница между двумя значениями = 67,8%

Точно так же вы можете попробовать калькулятор процентной разницы, чтобы найти процентную разницу для следующих значений.

• Начальное значение = 80, конечное значение = 280
• Начальное значение = 220, Конечное значение = 120

☛ Математические калькуляторы:

Как рассчитать площадь отрезка круга

Чтобы вычислить площадь сегмента, ограниченного хордой и дугой, образованной углом θ , сначала вычислите площадь треугольника, а затем вычтите ее из площади сектора, получив площадь сегмента. (см. диаграммы ниже)

Треугольник с углом θ можно разделить пополам, получив два прямоугольных треугольника с углами θ / 2.

грех ( θ / 2) = а / R

Таким образом, a = Rs в ( θ / 2) (длина шнура c = 2 a = 2 Rs в ( θ / 2)

cos ( θ / 2) = b / R

Итак, b = Rc os ( θ / 2)

Площадь треугольника XYZ равна половине основания на высоту перпендикуляра, поэтому, если основание является хордой XY, половина основания равна a, а высота перпендикуляра b. Итак, площадь такая:

ab

Подстановка на a и b дает:

Также площадь сектора составляет:

R 2 ( θ / 2)

А площадь сегмента — это разница между площадью сектора и треугольника, поэтому вычитание дает:

Площадь сегмента = R 2 ( θ / 2) — (1/2) R 2 sin θ

= ( R 2/2) ( θ — грех θ )

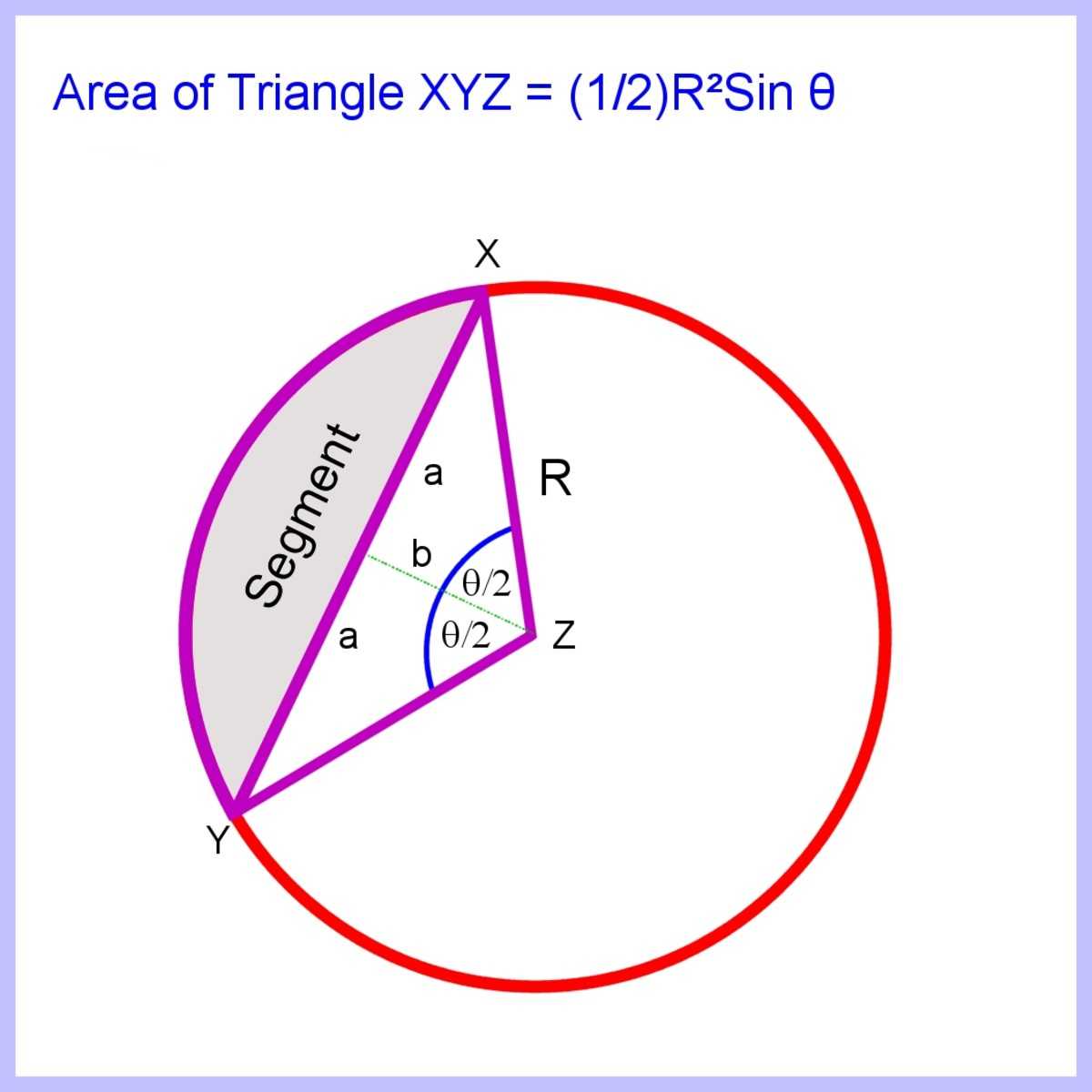
Чтобы вычислить площадь сегмента, сначала вычислите площадь треугольника XYZ, а затем вычтите ее из сектора.

Изображение Юджин Бреннан

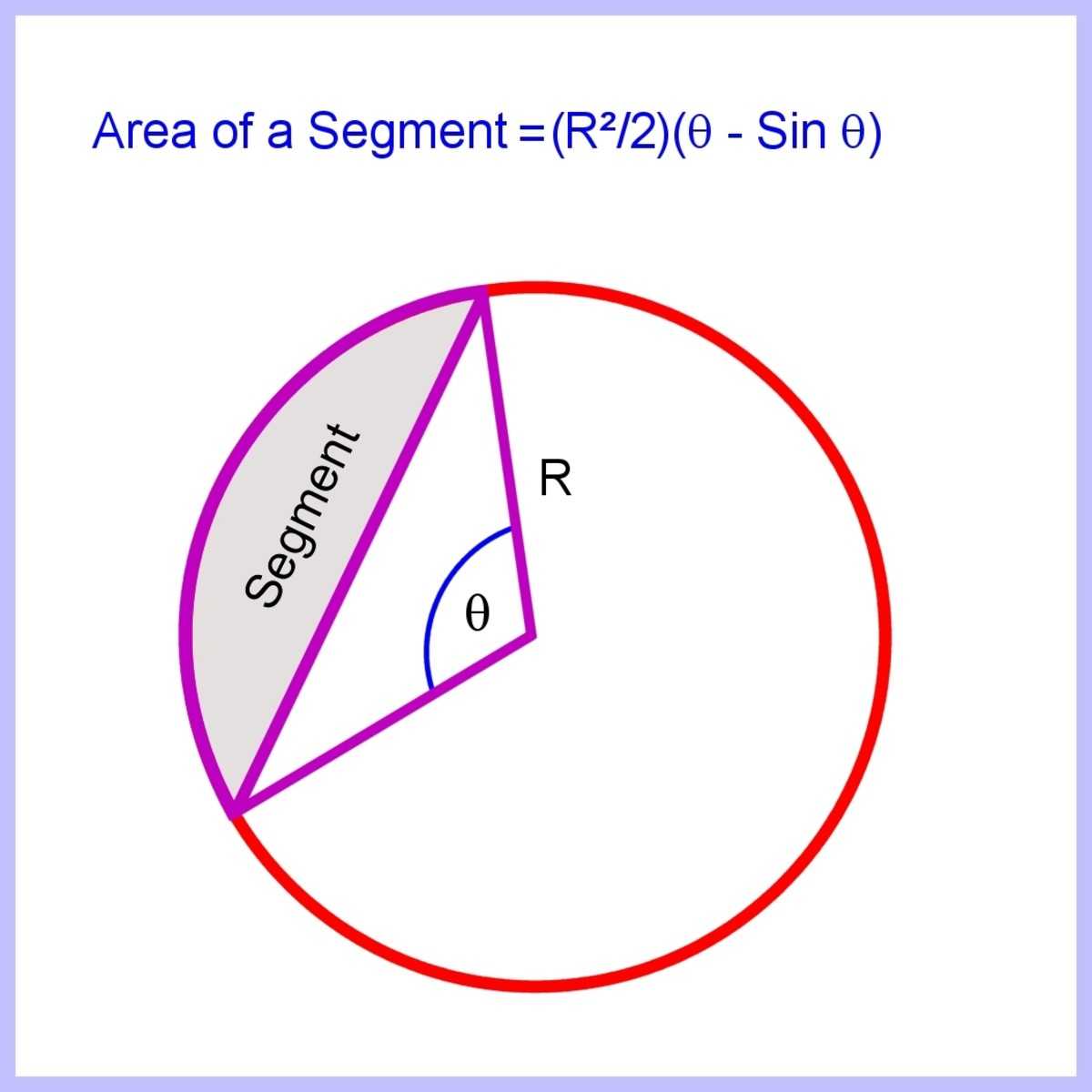
Площадь сегмента круга, зная угол

Изображение Юджин Бреннан