Основные свойства углов
- Все вписанные углы, которые опираются на одну дугу — равны.
- Вписанний угол, который опирается на диаметр будет прямым (90°).
- Вписанный угол равен половине центрального угла, что опирается на ту же дугу
β = α2
Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.
α + β = 180°
Дуга окружности (◡) — часть окружности, которая соединяет две точки на окружности.Определение.Градусная мера дуги — угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла,который ограничивает эту дугу своими сторонами.
Формула длины дуги через центральный угол (в градусах):
l = πr180°∙ α
Определение.Полуокружность — дуга в которой концы соединены диаметром окружности.Определение.Полукруг (◓) — часть круга, которая ограничена полуокружностью и диаметром.Определение.Сектор (◔) — часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.
Формула.Формула площади сектор через центральный угол (в градусах)
S = πr2360°∙ α
Сегмент — часть круга, которая ограничена дугой и хордой, что соединяет ее концы. Концентрические окружности — окружности с различными радиусами, которые имеют общий центр.
Кольцо — часть плоскости ограниченная двумя концентрическими окружностями.
Как ускорить процесс обучения: советы специалистов
Есть несколько простых рекомендаций, которые помогают значительно ускорить учебный процесс, помогают быстрее освоиться с тем, как искать площадь круга по разным известным параметрам.
К ним относятся такие, как:
- Убедитесь в том, что ребенок хорошо понимает основные определения. Педагогическая практика показывает, что дети часто путают радиус и диаметр, что приводит к появлению ошибок и выставлению низких оценок учителями.
- В геометрии очень важна наглядность. Все задачи стоит решать исключительно вместе с рисунками круга на бумаге. Это также поможет ребенку значительно быстрее освоиться с использованием циркуля, линейки. Такие навыки сильно помогут в учебе в будущем.
- Не показывайте ученику своего непонимания предмета. Он всегда должен видеть в вас человека, который обладает уверенными знаниями по такому вопросу. Не стоит демотивировать его, рассказывать о бесполезности расчетов.
- Хорошее понимание предмета достигается исключительно через многократное решение задач. Их вы сможете без труда составить своими силами. Все что нужно – ставить условие поиска площади с разными исходными параметрами – длиной окружности, диаметром, радиусом и другими.
- Усложните задачи через введение разных параметров обозначения площади. Есть множество вариантов прописывания площади – это квадратные сантиметры, миллиметры, метры, дециметры и километры. Хорошей математической тренировкой станет перевод разных значений друг в друга. Также можно попробовать посчитать в гектарах. Все это помогает в таких предметах, как геометрия, тригонометрия и математика.
Вычисление радиуса
Радиус можно посчитать разными способами.
Если известна длина окружности круга
Также несложно будет узнать радиус, если известна длина окружности круга. Формула для расчета длины окружности C=2πr, в которой C является длиной окружности, π=3,14, а r — это как раз искомый радиус.
Преобразовав данную формулу, получим: r=C/2π. Вообще, число «Пи» в формуле — это постоянное значение, округленное до 3,14. На самом деле «Пи» выглядит так:

Означает данное значение отношение длины окружности к диаметру той же окружности.
Если известна площадь круга
Формула площади круга выглядит так: A= π(r²). Эту формулу можно преобразовать в формулу радиуса:
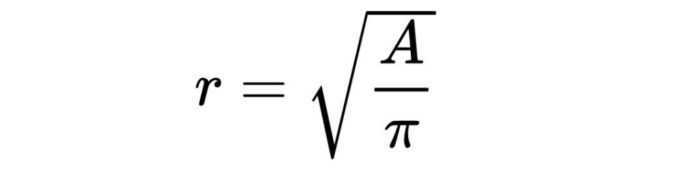
В ней A — это площадь круга, число «Пи» мы уже знаем, оно равно округленно 3,14, а r — это и есть искомое значение радиуса.
Как найти радиус круга, все школьники учат на геометрии. Взрослые, конечно, со временем забывают эти формулы. Но, прочитав данную статью, радиус круга может найти каждый: и взрослый, и ребенок.
👉🏻 Что такое окружность?
Описание длины окружности
Окружность – одна из самых известных геометрических фигур. С её помощью мы можем объяснить множество явлений, которые встречаются нам в повседневной жизни. Например, мы можем использовать её для измерения углов и расстояний, а также для создания кривых форм в дизайне и архитектуре. В данной статье мы рассмотрим, что такое окружность, как она строится и для чего она используется.
️ Описание
Окружность – это геометрическая фигура, которая представляет собой множество точек на плоскости, расположенных на одинаковом расстоянии от центра. Радиус окружности – это расстояние от центра до любой точки на окружности. Диаметр (d) – это расстояние между двумя точками на окружности, проходящими через её центр. Длина окружности (L) – это расстояние, которое необходимо пройти по окружности. Она вычисляется по формуле L = 2πr, где π – число «пи», примерно равное 3,14.
️ Построение
Существуют различные методы построения окружности, одним из которых является следующий:
- На плоскости нарисуйте точку А – центр будущей окружности.
- Найти точку В – любую точку на будущей окружности.
- Найдите расстояние от точки А до точки В – это будет радиус окружности .
- Найдите любую другую точку С на будущей окружности.
- Найдите расстояние между точками В и С – это будет диаметр окружности (d).
️ Использование
Окружность используется в различных областях науки, техники и искусства. Например:
- В математике и геометрии окружность – это одна из основных фигур. Многие теоремы и формулы связаны с окружностью (например, теорема Пифагора, формула площади круга).
- В физике окружность используется для измерения углов и расстояний. Для этих целей используются инструменты, такие как гониометры и микрометры.
- В технике окружность используется при проектировании колес и шестерен – они имеют форму окружности, чтобы обеспечивать определённое соотношение скоростей.
- В искусстве окружность может быть использована для создания кривых форм и изображений. Например, галерея Гуггенхайма в Нью-Йорке имеет форму окружности.
- Кроме того, в различных религиозных символах окружность играет важную роль (например, мандалы в буддизме или знак ом в индуизме).
Итак…
Окружность – это геометрическая фигура, которая имеет множество применений в различных областях знания. Она является основой для множества теорем и формул, а также используется в технике и искусстве для создания различных форм и изображений. Окружность – это не только абстрактная фигура, но и ежедневный предмет изучения в различных науках.
Площади усеченных частей круга
А также полезно знать следующие геометрические элементы, связанные с кругами и окружностями:
Хорда — отрезок, соединяющий любые две точки окружности.
Сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сектор является частью круга, а его площадь относится к площади круга так же, как и длина окружности сектора к длине всей окружности. Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.
Но площадь сектора можно вычислить и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:
где S — площадь сектора, r — радиус круга.
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой.
Площадь сегмента можно найти по формулам:
где S — площадь сегмента, sinα — синус угла двух между радиусов до концов хорды, r — радиус круга.
Часто задаваемые вопросы о площади круга?
И конечно, стоит ответить на некоторые вопросы, которые возникают во время расчетов.
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разнообразные калькуляторы, в частности калькуляторы: длины окружности, диаметра и площади круга. Для последней калькулятор находится на данной странице.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Кто впервые научился вычислять площадь круга?
Гиппократ Хиосский (не тот, в честь которого назвали клятву) первым сформулировал, что площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение. А Архимед в III веке до н. э. нашёл число Пи и продемонстрировал, что оно чуть меньше, чем 3 и 1/7.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Круг и окружность
В геометрии есть 2 фигуры, которые, вроде бы очень похожи, но при этом отличаются. И отличия заключаются не только во внешнем виде, но и в формулах вычисления отдельных элементов данных фигур.
Окружность
По своей сути окружность — это всего лишь линия, а точнее, кривая линия, начало и конец которой совпадают (замкнутая линия).
Все точки этой кривой удалены на равное расстояние от центра. Этот центр находится в той же плоскости, что и кривая. Внутри окружности ничего нет. То есть имеется центр и имеется линия, проведенная вокруг этого центра на определенном расстоянии.
Круг
Круг — это практически та же самая окружность, проведенная на определенном расстоянии от центра, но область между линией и центром заполнена множеством точек, которые находятся на расстоянии от центра, не большем, чем радиус этого круга.

Площадь круга
Определение 4
Круг — часть плоскости, ограниченной окружностью.
Выведем формулу для вычисления площади круга.
Рассмотрим следующую ситуацию. Пусть нам дана окружность с радиусом $R$. Обозначим её площадь через $S$. В нее вписан правильный -угольник с площадью $S_n$, в который, в свою очередь вписана окружность с площадью ${S’}_n$ (рис. 3).
Рисунок 3.
Из рисунка очевидно, что
Используем следующую известную формулу для правильного многоугольника:
Будем теперь неограниченно увеличивать число сторон правильного многоугольника. Тогда, при $n\to \infty $, получим
Тогда
По формуле, площадь правильного многоугольника равна $S_n=\frac{1}{2}P_nr$, $P_n\to 2\pi R$, следовательно
Формула (3) и есть формула для вычисления площади круга.
Как найти радиус окружности если известна только длина окружности
В данной публикации мы рассмотрим, как можно вычислить радиус круга (окружности) и разберем примеры решения задач для закрепления материала.
Формулы вычисления радиуса круга
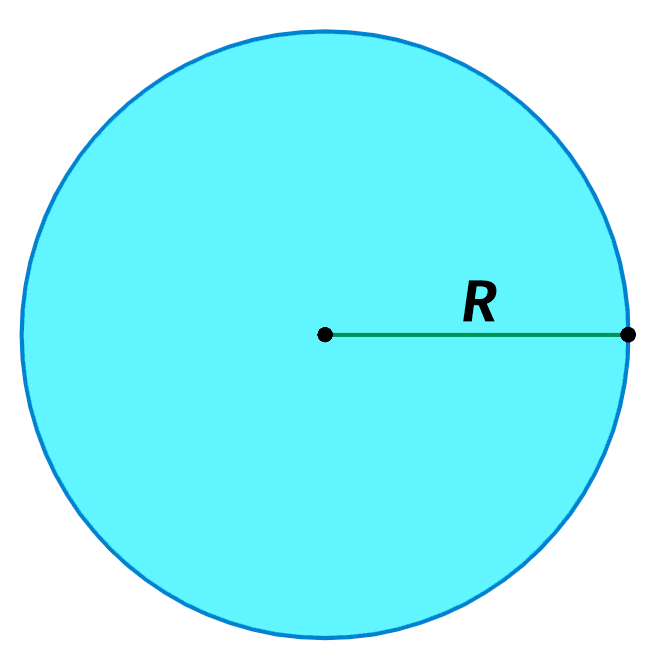
1. Через длину окружности/периметр круга
Радиус круга/окружности рассчитывается по формуле:
C – это длина окружности/периметр круга; равняется удвоенному произведению числа π на его радиус:
C = 2 π R
π – число, приближенное значение которого равно 3,14.
2. Через площадь круга
Радиус круга/окружности вычисляется таким образом:
S – это площадь круга; равна числу π , умноженному на квадрат его радиуса:
S = π R 2
Примеры задач
Задание 1 Длина окружности равняется 87,92 см. Найдите ее радиус.
Решение: Используем первую формулу (через периметр):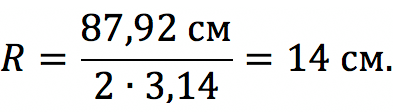
Задание 2 Найдите радиус круга, если его площадь составляет 254,34 см 2 .
Решение: Воспользуемся формулой, выраженной через площадь фигуры: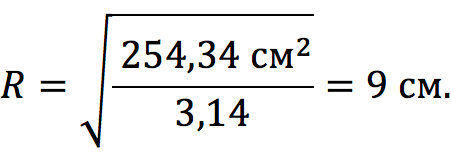
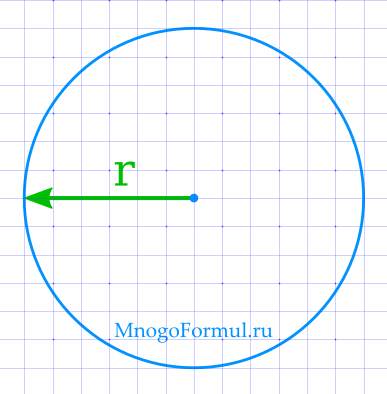
Формула для нахождения длины окружности через радиус:
, где r — радиус окружности.
Радиус и диаметр
Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.
А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:
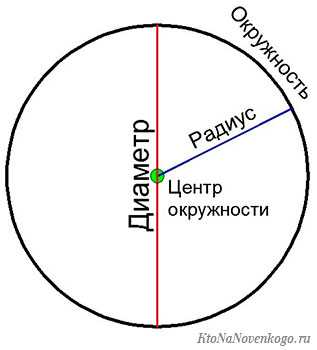
Обозначается диаметр также первой буквой своего слова – D или d.
Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.
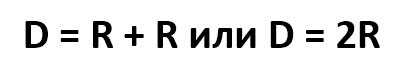
Вычисление радиуса
Радиус можно посчитать разными способами.
Если известна длина окружности круга
Также несложно будет узнать радиус, если известна длина окружности круга. Формула для расчета длины окружности C=2πr, в которой C является длиной окружности, π=3,14, а r — это как раз искомый радиус.
Преобразовав данную формулу, получим: r=C/2π. Вообще, число «Пи» в формуле — это постоянное значение, округленное до 3,14. На самом деле «Пи» выглядит так:

Означает данное значение отношение длины окружности к диаметру той же окружности.
Если известна площадь круга
Формула площади круга выглядит так: A= π(r²). Эту формулу можно преобразовать в формулу радиуса:
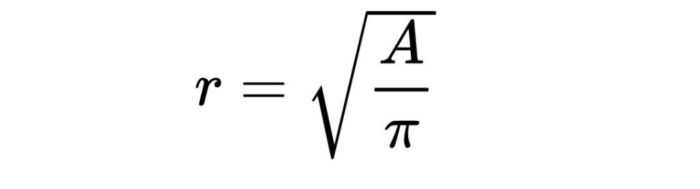
В ней A — это площадь круга, число «Пи» мы уже знаем, оно равно округленно 3,14, а r — это и есть искомое значение радиуса.
Как найти радиус круга, все школьники учат на геометрии. Взрослые, конечно, со временем забывают эти формулы. Но, прочитав данную статью, радиус круга может найти каждый: и взрослый, и ребенок.
Способ расчета радиуса круга:
Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга). Формула радиуса круга: где P – длина окружности, pi – число π, равное примерно 3.14
Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга). Формула радиуса круга: где S – площадь круга, pi – число π, равное примерно 3.14
Через сторону описанного квадрата
Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
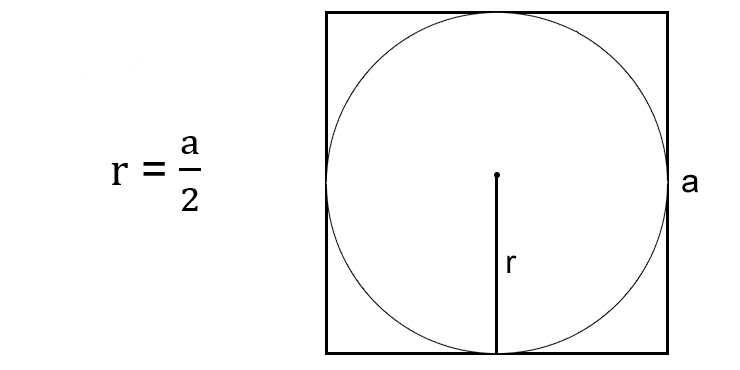
- r — искомый радиус окружности.
- a — сторона описанного квадрата.
Формула
r = C /2π , где π ≈ 3.14
Свойства радиуса
В отношении радиуса действуют несколько важных правил:
- Радиус составляет половину диаметра. Это мы продемонстрировали только что.
- У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.
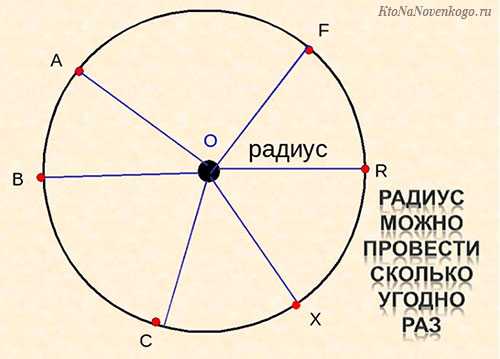
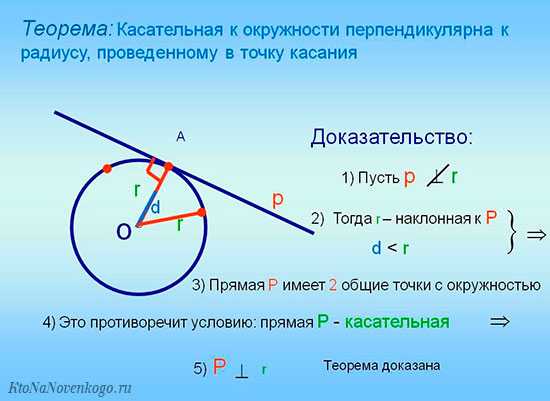
Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.
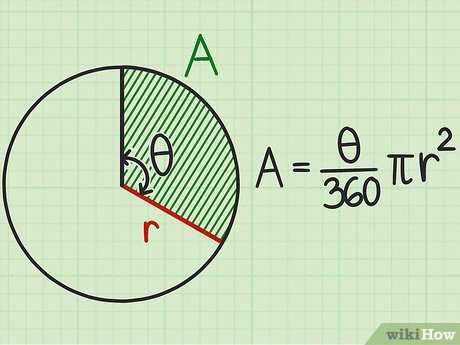
По площади сектора и центральному углу
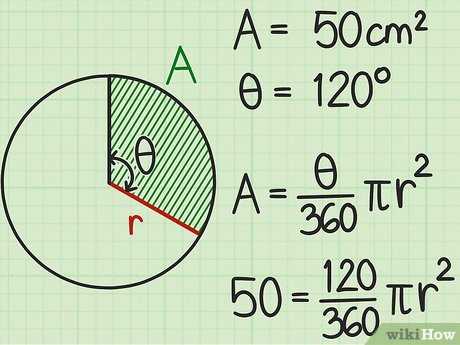
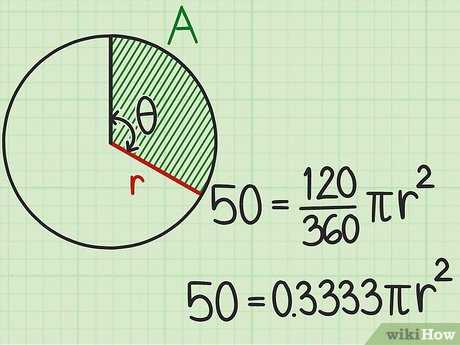
Например, если площадь сектора равна 50 см 2 , а центральный угол равен 120 градусов, формула запишется следующим образом: .
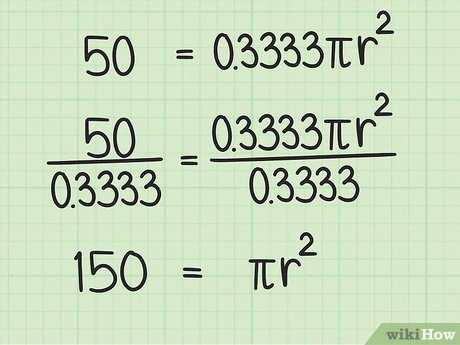

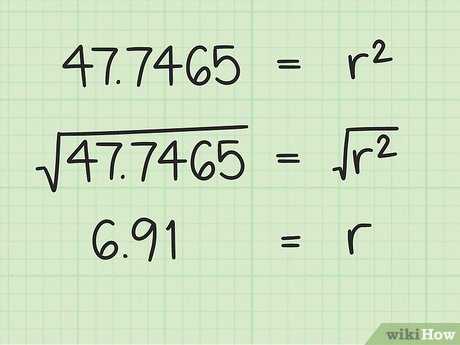
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла .
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах , получаем
В случае, когда величина α выражена в в радианах , получаем
Формулы для площади круга и его частей
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |
где R – радиус круга, D – диаметр круга
если величина угла α выражена в радианах
если величина угла α выражена в градусах
если величина угла α выражена в радианах
если величина угла α выражена в градусах
| Площадь круга |
где R – радиус круга, D – диаметр круга
Площадь сектора
если величина угла α выражена в радианах
если величина угла α выражена в градусах
Площадь сегмента
Примеры задач с решением
Задача № 1
Найдите площадь круга, если известно, что длина окружности составляет 85 миллиметров.
Решение:
Произведем расчеты на основании известной формулы:
\(S=\frac{\mathrm L^2}{4\mathrm\pi}\)
\(S=\frac{\mathrm L^2}{4\mathrm\pi}=\frac{85^2}{4\cdot13,14}=\frac{7225}{52,56}=137,46\)
Ответ: 137,46 мм2.
Задача № 2
Детская песочница имеет квадратную форму со стороной, равной 1,5 метрам. По технологии песочницу устанавливают на прорезиненном участке круглой формы, равном кругу, в который можно вписать такую песочницу. Найдите площадь территории, на которую нужно уложить резиновую крошку.
Решение:
Воспользуемся формулой: \(S=0,5a^2\mathrm\pi=0,5\cdot1,5^2\cdot13,14=14,7825 \)
Как вычислить радиус и диаметр окружности через площадь круга?
Площадь круга — это показатель, который характеризует площадь поверхности, ограниченной окружностью. Чтобы найти радиус и диаметр окружности по известной площади круга, нужно использовать математические формулы.
Для начала, необходимо знать формулу для вычисления площади круга. Она выглядит следующим образом: S = π * r^2, где S — площадь круга, π (пи) — математическая константа, равная примерно 3.14159, r — радиус окружности.
Окружность — это геометрическая фигура, состоящая из всех точек, равноудаленных от центра. Радиус окружности — это расстояние от центра окружности до любой точки на ее границе.
Чтобы найти радиус по известной площади круга, необходимо воспользоваться формулой: r = √(S / π), где r — радиус, S — площадь круга, π — математическая константа.
Диаметр окружности — это расстояние между двумя противоположными точками на границе окружности. Он является удвоенным радиусом (d = 2r).
Таким образом, чтобы найти диаметр по известной площади круга, можно применить следующую формулу: d = 2 * √(S / π), где d — диаметр, S — площадь круга, π — математическая константа.
Пример задачи на понятие окружности
Пример 1
Найти уравнение окружности с центром в точке $(1,\ 1)$. проходящей через начало координат, найти длину данной окружности и площадь круга, ограниченного данной окружностью.
Решение.
Найдем сначала уравнение данной окружности. Для этого будем использовать формулу (1). Так как центр окружности лежит в точке $(1,\ 1)$, получим
\
Найдем радиус окружности как расстояние от точки $(1,\ 1)$ до точки $(0,0)$
\
Получаем, уравнение окружности имеет вид:
\
Найдем длину окружности по формуле (2). Получим
\
Найдем площадь по формуле (3)
\
Ответ: ${(x-1)}^2+{(y-1)}^2=2$, $C=2\sqrt{2}\pi $, $S=2\pi $
Формулы квадрата
Для расчёта всех основных параметров квадрата воспользуйтесь калькулятором.
Свойства квадрата
- Длины сторон квадрата равны.
- Все углы квадрата прямые, равны 90°.
- Противолежащие стороны квадрата параллельны друг другу.
- Сумма всех углов квадрата равна 360°.
- Величина угла между диагональю и стороной равна 45°.
- Диагонали квадрата — тождественны, перпендикулярны и разделяются точкой пересечения пополам.
- Каждая из диагоналей делит квадрат на два равнобедренных прямоугольных треугольника.
- Обе диагонали делят квадрат на 4 равнобедренных прямоугольных треугольника.
- Пересечение диагоналей является центром вписанной и описанной окружности.
Сторона квадрата
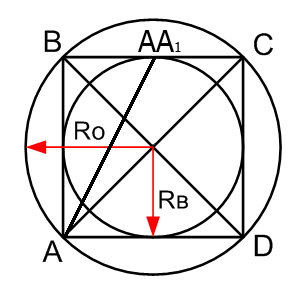
| Где: | AB – сторона квадрата |
| AC(BD) – диагональ квадрата | |
| RВ – радиус вписанной окружности | |
| RO – радиус описанной окружности | |
| AA1 — линия выходящая из угла на середину стороны квадрата |
Стороны квадрата через диагональ
Стороны квадрата через радиус вписанной окружности
Стороны квадрата через радиус описанной окружности
Стороны квадрата через площадь, S
Стороны квадрата через периметр, P
Стороны квадрата через линию выходящую из угла на середину стороны квадрата, AA1
Углы
Центральный угол
Если длина дуги составляет $\theta$ градуов или радиан, то значение центрального угла также $\theta$ (градусов или радиан).
Если вы знаете длину дуги (в дюймах, ярдах, футах, сантиметрах, метрах …) вы можете найти значение её соответствующего центрального угла ($\theta$) по формуле:
$l$ — длина дуги.
Вписанный угол
Вписанный угол это угол с вершиной на окружности и со сторонами, которые содержат хорды окружности. На рисунке, угол APB это вписанный угол.
Пример: $\widehat{AB} = 84^\circ$ $\angle APB = \frac{84}{2} = 42^\circ$
Углы между двумя хордами
Случай 1: два секущие пересекаются внутри окружности.
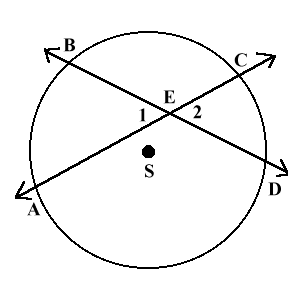
Когда две секущие пересекаются внутри окружности, величина образованных угла, в два раза меньше суммы величин дуг, на которые они опираются. На рисунке дуга AB и дуга CD равны 60° и 50° тогда углы 1 и 2 равны $\frac{1}{2}(60^\circ + 50^\circ)=55^\circ$
Случай 2: две секущие пересекаются вне окружности.
Иногда секущие пересекаются за пределами окружности. Когда это случается, величина образующихся углов равна половине разности дуг, на которые они опираются.
$\angle ABC =\frac{1}{2}(x — y)$
На рисунке дуга AB=80° и дуги CD=30°. $\angle ABC = \frac{1}{2}(80 — 30) = \frac{1}{2} \cdot 50 = 25^\circ$
Примеры решения задач
Задача 1
Имеется некая окружность с радиусом 12 см. Необходимо вычислить, чему равна длина этой окружности.
Решение
Зная, что вычислить длину окружности при известном ее радиусе можно по стандартной формуле, подставим в выражение числовые значения и запишем ответ:
\(C = 2 \cdot 3,14 \cdot 12 = 75,36\)
Ответ: 75,36 см.
Задача 2
Диаметр окружности равен 15 см. Нужно определить периметр круга, который ограничен этой окружностью.
Решение
Периметр круга в данном случае соответствует длине окружности. Вычислить искомую величину можно, зная диаметр окружности:
\(C = 3,14 \cdot 15 = 47,1\)
Ответ: 47,1 см.
Задача 3
Окружность обладает длиной, равной 12. Ее центр обозначен буквой О. Угол \(\angle AOB\) составляет \(120^{\circ}\). С помощью точек А и В, которые принадлежат окружности, она делится на пару дуг. Требуется вычислить, во сколько раз длина максимальной из образованных дуг больше по сравнению с длиной меньшей.
Решение
Известно, что отношение длин дуг соответствует отношению их градусных мер. Зная, что О является центральной точкой окружности, определим \(\angle AOB\), как центральный. Дуга по градусной мере меньше по сравнению с полуокружностью. Ее градусная мера соответствует градусной мере центрального угла, опирающегося на эту дугу. Меньшая дуга равна \(120^{\circ}\), а градусная мера максимальной дуги составляет \(240^{\circ}\). Таким образом:
\(240 \div 120 = 2\)
Ответ: 2.
Задача 4
На рисунке изображена окружность с центральной точкой О. Длина этой окружности составляет 18 см. Сектор АОВ обладает площадью \(\dfrac{18}{\pi}см^2\). Требуется определить, чему равна длина дуги АВ рассматриваемого сектора.
Решение
Запишем формулу для вычисления длины окружности при ее известном радиусе:
\(С = 2\pi R\)
Согласно условию задачи:
\(18 = 2\pi R\)
В таком случае:
\(R = \dfrac{9}{\pi}\)
Площадь сектора, градусная мера дуги которого составляет \(\alpha\), равна:
\(\pi R^2 \cdot \dfrac{\alpha}{360}\)
Тогда запишем выражение для расчета длины дуги с градусной мерой \(\alpha\):
\(2\pi R\cdot \dfrac{\alpha}{360}\)
Если умножить площадь сектора с дугой, равной \(\alpha\), на \(\dfrac{2}{R}\), то получится определить длину дуги с градусной мерой \(\alpha\). В результате длина дуги АВ рассматриваемого сектора составляет:
\(\dfrac{18}{\pi} \cdot \dfrac{2\pi}{9} = 4\)
Ответ: 4 см.
Задача 5
На рисунке изображено пересечение пары окружностей. Требуется вычислить длину внешней границы фигуры, которая получилась в результате. Длина окружности составляет 12.
Решение
Проведем отрезок через центральные точки окружностей. Соединим центры этих фигур с точками, в которых окружности взаимно пересекаются. Заметим, что можно сформировать пару равносторонних треугольников со сторонами, равными радиусам рассматриваемых окружностей.
Дуга, принадлежащая одной окружности, которая находится внутри сформированной фигуры, имеет опору в виде угла. Этот угол равен паре углов, принадлежащих равностороннему треугольнику, и составляет \(120^\circ\). Таким образом, длину этой дуги допустимо вычислить по следующей формуле:
\(\frac{C_{120^\circ}}{12} = \frac{120^\circ}{360^\circ} \Rightarrow C_{120^\circ} = 4\)
В результате длина внешней границы при пересечении окружностей составляет:
\(L = 2\cdot C — 2\cdot C_{120^\circ} = 2\cdot12 — 2\cdot 4 = 16\)
Ответ: 16.
Задача 6
На рисунке изображена окружность с некоторыми известными величинами. Требуется рассчитать меру \(\angle AOB\).
Решение
Запишем, чему равна общая длина окружности:
С = 1 + 2 + 5 + 10 = 18
В таком случае упрощается нахождение искомого угла:
\(\frac{C_{\angle AOB}}{C} = \frac{\angle AOB}{360^\circ} \Rightarrow \frac{5}{18} = \frac{\angle AOB}{360^\circ} \Rightarrow \angle AOB = 100^\circ\)
Способ Эрастофена
Эрастофен жил в городе Александрия, расположенном на севере Египта неподалеку от устья реки Нил на побережье Средиземного моря. Он знал, что в определенный день всего года в городе Сиена на юге Египта на дне колодцев не было ясной тени. То есть Светило в тот момент находится прямо над головой. Впрочем в Александрии, располагавшейся севернее Сиены, даже в день летнего солнцестояния Светило никогда не бывает прямо над головой. Эрастофен осознал, что дозволено определить, насколько Светило смещено от расположения «прямо над головой», измерив угол, образованный тенью от вертикального объекта. Он измерил длину тени от высокой башни в Александрии и, применяя геометрию, вычислил угол между тенью и вертикальной башней. Он оказался равен приблизительно 7,2 градуса.Дальше Эрастофен применял больше трудные геометрические построения. Предположил, что угол от тени верно такой, как между Александрией и Сиеной, если считать от центра Земли. Для комфорта посчитал, что 7,2 градуса составляет 1/50 часть полного круга. Дабы обнаружить длину окружности Земли, оставалось расстояние между Сиеной и Александрией умножить на 50. По данным Эрастофена, расстояние между городами составляло 5 тыс. стадиев. Но всеобщей единицы длины в те дальнии времена не существовало, и сегодня неведомо, каким именно стадием пользовался Эрастофен. Если он использовал египетский, составлявший 157,5 м, радиус Земли равнялся 6287 км. Погрешность в таком случае была 1,6%. А если применял больше общеизвестный греческий стадий, равный 185 м, погрешность составляла бы 16,3%. В любом случае точность вычислений достаточно отличная для того времени.
Площадь круга
Напомним, что кругом называется часть плоскости, ограниченная окружностью. Для нахождения площади круга можно использовать все тот же метод многоугольников, который мы применили для нахождения длины окружности и вычисления числа π.
Возьмем окружность и впишем в нее n-угольник. В свою очередь в него впишем окружность.
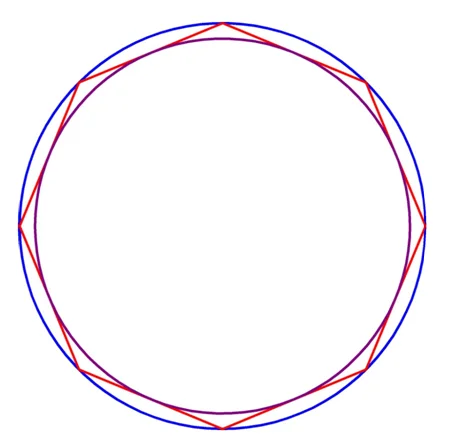
Выпишем изученные нами ранее две формулы:
Здесь r и R – радиусы вписанной и описанной окружности соответственно, Р – периметр многоугольника, Sмног. – площадь многоугольника. С ростом n периметр многоугольника приближается к длине описанной окружности, что можно записать в таком виде

Одновременно с этим и площадь многоугольника приближается к площади круга (имеется ввиду больший, то есть описанный круг), что позволяет вычислить ее:

Задание. Определите площадь круга, ограниченного окружностью 10 см.
Решение. В этой задаче надо просто подставить числа в формулу:
![]()
Ответ: 100π см2.
Задание. Площадь круглого бассейна составляет 10 м2. Каков его радиус? При расчете примите число π равным 3,14.
Решение. Здесь надо из формулы площади получить выражение для вычисления радиуса:
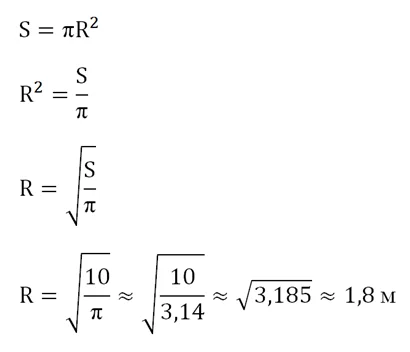
Ответ: ≈ 1,8 м.
Задание. Во сколько раз увеличится площадь круга, если его радиус увеличится в 2 раза?
Решение. Пусть радиус исходного круга – это R. Тогда его площадь рассчитывается так:

Ответ: в 4 раза.
Примечание. В общем случае увеличение радиуса круга в k раз приводит к увеличению его площади в k2 раз.
Задание. Ваня и Петя решили купить пиццу. Сначала Ваня заметил пиццу диаметром 30 см, цена которой – 300 рублей. Но тут же Петя обнаружил на витрине такую же пиццу диаметром 40 см, которая стоила уже 450 рублей, и предложил ее купить. Ваня сказал, что этот невыгодная покупка, ведь радиус у второй пиццы больше только на треть, а цена больше уже наполовину. Прав ли Ваня?
Решение. Масса пиццы пропорциональна их площади. У второй пиццы радиус больше в 4/3 раза (так как 40/30 = 4/3), значит, площадь у нее больше в
Получается, что вторая пицца больше в 1,78 раза, а цена у нее выше только в 1,5 раза. То есть выгодней купить именно вторую, то есть большую пиццу.
Ответ: Ваня не прав, лучше купить пиццу диаметром 40 см.
Примечание. В этой задаче можно было посчитать площадь каждой пиццы, а потом поделить их стоимость на площадь и получить цену 1 см2 пиццы в каждом варианте. Ответ бы при этом не изменился.
Задание. Завод изготавливает круглые столы радиусом 1,5 метра. Их поверхность надо покрывать лаком, причем на каждый 1 м2 поверхности необходимо тратить 20 г лака. Лак закупается раз в месяц, и в течение ближайшего месяца завод должен изготовить 5000 столов. Сколько лака должен закупить завод на ближайший месяц?
Решение. Считаем площадь поверхности каждого стола:

Ответ: 706,5 кг.
Практическое применение нахождения радиуса окружности
1. Инженерия и архитектура:
- Расчет радиуса колеса для различных видов транспорта;
- Расчет размеров кругов, используемых в архитектуре;
- Расчет размеров труб и других объектов, имеющих форму круга.
2. Медицина:
- Расчет радиуса линз для очков;
- Расчет размеров катетеров.
3. Физика и математика:
- Расчет радиуса кривизны при моделировании;
- Расчет объема шаровой частицы в физических и математических моделях.
4. Производство:
- Расчет радиуса гибких труб и рукавов;
- Расчет размеров колец и пружин, используемых в производстве.
Всегда полезно знать, как найти радиус окружности, зная ее длину, так как это позволяет избежать дополнительных расчетов и сэкономить время и силы.

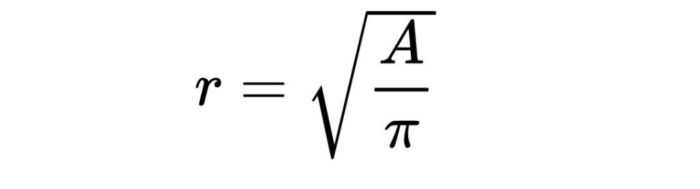



![Math-public:dlina-okruzhnosti-ploshchad-kruga [президентский фмл №239]](http://rwvt.ru/wp-content/uploads/4/f/e/4fe52c44a1a3a7964b41e7fcb3b5293f.jpeg)

























