Векторное произведение — определения, свойства, формулы, примеры и решения

Линейные операции над геометрическими векторами

Умножение вектора на число

Произведением вектора на число
называется вектор, получающийся из вектора растяжением
(при ) или сжатием (при )
в раз, причём направление вектора
сохраняется, если ,
и меняется на противоположное, если . (Рис. 2)

Из определения следует, что векторы и =
всегда расположены на одной или на параллельных прямых. Такие векторы называются коллинеарными. (Можно говорить также, что эти векторы параллельны, однако в векторной алгебре принято говорить «коллинеарны».) Справедливо и обратное утверждение:
если векторы и коллинеарны,
то они связаны отношением

.   (1)

Следовательно, равенство (1) выражает условие коллинеарности двух векторов.

Сложение и вычитание векторов

При сложении векторов нужно знать, что суммой векторов и
называется вектор , начало которого
совпадает с началом вектора , а конец — с концом вектора ,
при условии, что начало вектора приложено к концу вектора . (Рис. 3)

Это определение может быть распределено на любое конечное число векторов. Пусть в пространстве даны n
свободных векторов . При сложении
нескольких векторов за их сумму принимают замыкающий вектор, начало которого
совпадает с началом первого вектора, а конец — с концом последнего вектора. То есть, если к концу вектора
приложить начало вектора , а к концу вектора
— начало вектора и т.д. и, наконец, к концу вектора
— начало вектора , то
суммой этих векторов служит замыкающий вектор , начало которого совпадает с началом первого вектора
, а конец — с концом последнего вектора . (Рис. 4)

Слагаемые называются составляющими вектора , а
сформулированное правило — правилом многоугольника. Этот многоугольник может и не быть плоским.

При умножении вектора на число -1 получается противоположный вектор
.
Векторы и имеют одинаковые длины и противоположные направления.
Их сумма даёт нулевой вектор,
длина которого равна нулю. Направление нулевого вектора не определено.

В векторной алгебре нет необходимости рассматривать отдельно операцию вычитания: вычесть из вектора
вектор
означает прибавить к вектору противоположный вектор
, т.е.

Пример 1. Упростить выражение:

.

Решение:

,

то есть, векторы можно складывать и умножать на числа так же, как и многочлены (в частности,
также задачи на упрощение выражений). Обычно необходимость упрощать линейно подобные выражения с векторами возникает перед
вычислением произведений векторов.

Пример 2. Векторы и
служат диагоналями параллелограмма ABCD (рис. 4а).
Выразить через и
векторы , ,
и ,
являющиеся сторонами этого параллелограмма.

Решение. Точка пересечения диагоналей параллелограмма делит каждую диагональ пополам.
Длины требуемых в условии задачи векторов находим либо как половины сумм векторов, образующих с искомыми треугольник, либо как половины разностей (в зависимости
от направления вектора, служащего диагональю), либо, как в последнем случае, половины суммы, взятой со знаком минус. Результат —
требуемые в условии задачи векторы:

Есть все основания полагать, что теперь Вы правильно ответили на вопрос о векторах «Предприимчивость»
и «Инновационные способности» в начале этого урока. Правильный ответ: над этими векторами производится
операция сложения.

Решить задачи на векторы самостоятельно, а затем посмотреть решения

Пример 3. Даны векторы
и
. Построить на
чертеже векторы 1) ,
2) ,
3) ,
4) .

Пример 4. Даны векторы
и
. Построить на
чертеже векторы 1) ,
2) ,
3) ,
4) .

Как найти длину суммы векторов?

Эта задача занимает особое место в операциях с векторами, так как
предполагает использование тригонометрических свойств. Допустим, Вам попалась задача
вроде следующей:

Даны длины векторов
и длина суммы этих векторов .
Найти длину разности этих векторов .

Решения этой и других подобных задач и объяснения, как их решать — в
уроке «Сложение векторов: длина суммы векторов и теорема косинусов».

А проверить решение таких задач можно на Калькуляторе
онлайн «Неизвестная сторона треугольника (сложение векторов и теорема косинусов)».

А где произведения векторов?

Произведения вектора на вектор не являются линейными операциями и рассматриваются отдельно. И у нас есть уроки «Скалярное произведение векторов» и «Векторное и смешанное произведения векторов».

Числовая проекция вектора на ось

Числовая характеристика проекции вектора на ось – числовая проекция вектора на заданную ось.

Числовой проекцией вектора на ось называют число, которое равно произведению длины данного вектора на косинус угла между данным вектором и вектором, который определяет направление оси.

Числовая проекция A B → на L имеет обозначение n p L A B → , а a → на b → — n p b → a → .

Исходя из формулы, получим n p b → a → = a → · cos a → , b → ^ , откуда a → является длиной вектора a → , a ⇀ , b → ^ — угол между векторами a → и b → .

Получим формулу вычисления числовой проекции: n p b → a → = a → · cos a → , b → ^ . Она применима при известных длинах a → и b → и угле между ними. Формула применима при известных координатах a → и b → , но имеется ее упрощенный вид.

Узнать числовую проекцию a → на прямую по направлению b → при длине a → равной 8 и углом между ними в 60 градусов. По условию имеем a ⇀ = 8 , a ⇀ , b → ^ = 60 ° . Значит, подставляем числовые значения в формулу n p b ⇀ a → = a → · cos a → , b → ^ = 8 · cos 60 ° = 8 · 1 2 = 4 .

Ответ: 4.

При известном cos ( a → , b → ^ ) = a ⇀ , b → a → · b → , имеем a → , b → как скалярное произведение a → и b → . Следуя из формулы n p b → a → = a → · cos a ⇀ , b → ^ , мы можем найти числовую проекцию a → направленную по вектору b → и получим n p b → a → = a → , b → b → . Формула эквивалента определению, указанному в начале пункта.

Числовой проекцией вектора a → на ось , совпадающей по направлению с b → , называют отношение скалярного произведения векторов a → и b → к длине b → . Формула n p b → a → = a → , b → b → применима для нахождения числовой проекции a → на прямую, совпадающую по направлению с b → , при известных a → и b → координатах.

Задан b → = ( — 3 , 4 ) . Найти числовую проекцию a → = ( 1 , 7 ) на L .

Решение

На координатной плоскости n p b → a → = a → , b → b → имеет вид n p b → a → = a → , b → b → = a x · b x + a y · b y b x 2 + b y 2 , при a → = ( a x , a y ) и b → = b x , b y . Чтобы найти числовую проекцию вектора a → на ось L , нужно: n p L a → = n p b → a → = a → , b → b → = a x · b x + a y · b y b x 2 + b y 2 = 1 · ( — 3 ) + 7 · 4 ( — 3 ) 2 + 4 2 = 5 .

Ответ: 5.

Найти проекцию a → на L , совпадающей с направлением b → , где имеются a → = — 2 , 3 , 1 и b → = ( 3 , — 2 , 6 ) . Задано трехмерное пространство.

Решение

По заданным a → = a x , a y , a z и b → = b x , b y , b z вычислим скалярное произведение: a ⇀ , b → = a x · b x + a y · b y + a z · b z . Длину b → найдем по формуле b → = b x 2 + b y 2 + b z 2 . Отсюда следует, что формула определения числовой проекции a → будет: n p b → a ⇀ = a → , b → b → = a x · b x + a y · b y + a z · b z b x 2 + b y 2 + b z 2 .

Подставляем числовые значения: n p L a → = n p b → a → = ( — 2 ) · 3 + 3 · ( — 2 ) + 1 · 6 3 2 + ( — 2 ) 2 + 6 2 = — 6 49 = — 6 7 .

Просмотрим связь между a → на L и длиной проекции a → на L . Начертим ось L , добавив a → и b → из точки на L , после чего проведем перпендикулярную прямую с конца a → на L и проведем проекцию на L . Существуют 5 вариаций изображения:

Первый случай при a → = n p b → a → → означает a → = n p b → a → → , отсюда следует n p b → a → = a → · cos ( a , → b → ^ ) = a → · cos 0 ° = a → = n p b → a → → .

Второй случай подразумевает применение n p b → a → ⇀ = a → · cos a → , b → , значит, n p b → a → = a → · cos ( a → , b → ) ^ = n p b → a → → .

Третий случай объясняет, что при n p b → a → → = 0 → получаем n p b ⇀ a → = a → · cos ( a → , b → ^ ) = a → · cos 90 ° = 0 , тогда n p b → a → → = 0 и n p b → a → = 0 = n p b → a → → .

Четвертый случай показывает n p b → a → → = a → · cos ( 180 ° — a → , b → ^ ) = — a → · cos ( a → , b → ^ ) , следует n p b → a → = a → · cos ( a → , b → ^ ) = — n p b → a → → .

Пятый случай показывает a → = n p b → a → → , что означает a → = n p b → a → → , отсюда имеем n p b → a → = a → · cos a → , b → ^ = a → · cos 180 ° = — a → = — n p b → a → .

Числовой проекцией вектора a → на ось L , которая направлена как и b → , имеет значение:

• длины проекции вектора a → на L при условии, если угол между a → и b → меньше 90 градусов или равен 0: n p b → a → = n p b → a → → с условием 0 ≤ ( a → , b → ) ^ 90 ° ;
• ноля при условии перпендикулярности a → и b → : n p b → a → = 0 , когда ( a → , b → ^ ) = 90 ° ;
• длины проекции a → на L , умноженной на -1, когда имеется тупой или развернутый угол векторов a → и b → : n p b → a → = — n p b → a → → с условием 90 ° a → , b → ^ ≤ 180 ° .

Дана длина проекции a → на L , равная 2 . Найти числовую проекцию a → при условии, что угол равен 5 π 6 радиан.

Решение

Из условия видно, что данный угол является тупым: π 2 5 π 6 π . Тогда можем найти числовую проекцию a → на L : n p L a → = — n p L a → → = — 2 .

Дана плоскость О х y z с длиной вектора a → равной 6 3 , b → ( — 2 , 1 , 2 ) с углом в 30 градусов. Найти координаты проекции a → на ось L .

Решение

Для начала вычисляем числовую проекцию вектора a → : n p L a → = n p b → a → = a → · cos ( a → , b → ) ^ = 6 3 · cos 30 ° = 6 3 · 3 2 = 9 .

По условию угол острый, тогда числовая проекция a → = длине проекции вектора a → : n p L a → = n p L a → → = 9 . Данный случай показывает, что векторы n p L a → → и b → сонаправлены, значит имеется число t , при котором верно равенство: n p L a → → = t · b → . Отсюда видим, что n p L a → → = t · b → , значит можем найти значение параметра t : t = n p L a → → b → = 9 ( — 2 ) 2 + 1 2 + 2 2 = 9 9 = 3 .

Тогда n p L a → → = 3 · b → с координатами проекции вектора a → на ось L равны b → = ( — 2 , 1 , 2 ) , где необходимо умножить значения на 3. Имеем n p L a → → = ( — 6 , 3 , 6 ) . Ответ: ( — 6 , 3 , 6 ) .

Необходимо повторить ранее изученную информацию об условии коллинеарности векторов.

Векторное произведение коллинеарных векторов

Случаи, при которых векторы являются коллинеарными:

• когда вектора возможно расположить на одной прямой;
• параллелограмм визуально, также становится плоским относительно оси координат;
• площадь параллелограмма равна нулю \(синус нуля равняется или 180 градусов равняется нулю следовательно и площадь также будет нулевой).

Поэтому , если \=\overline{0} \text{ и }|\bar{N}|=||=0\].

Нужно всегда помнить, что именно само векторное произведение равно нулю.

При решении практических задач данным моментом часто пренебрегают.

Пример частного случая \=\overline{0}\].

Векторное произведение помогает определить коллинеарность векторов трехмерного типа.

Определение смешанного произведения векторов

Определение: Смешанным произведением векторов называется число  – скалярное произведение a  на векторное произведение
Смешанное произведение обозначается так:

Пусть в некоторой пдск
Обозначим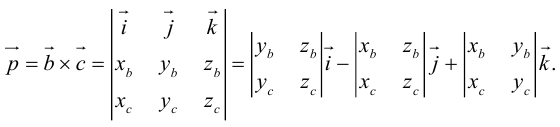      
Тогда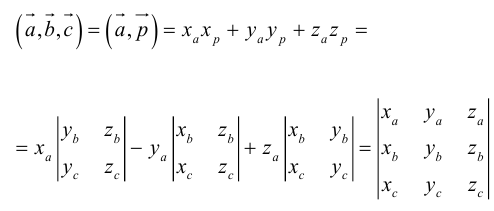   
по 7 свойству определителей. 
Таким образом,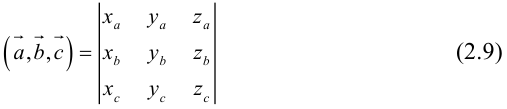                              
По  определению  скалярного  произведения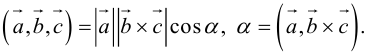 
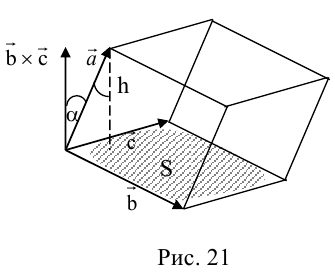
Совместим начала всех трех векторов в одной точке. Тогда (рис. 21)   – площадь параллелограмма,    – высота параллелепипеда,   – объем параллелепипеда.  

Геометрический  смысл  смешанного  произведения:  модуль  смешанного произведения численно равен объему параллелепипеда, построенного на векторах-сомножителях,  при  этом  –  правая  тройка,  и  – левая тройка. 
 

Свойства смешанного произведения

1. Необходимым и достаточным условием компланарности трех векторов является  равенство  нулю  их  смешанного  произведения:    компланарны  
 

Доказательство:   а) компланарны
Если компланарны, то на них нельзя построить параллелепипед, а потому
б)компланарны.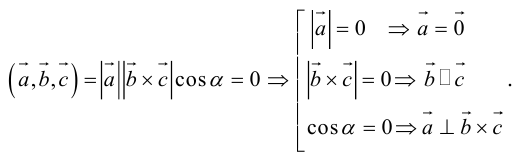   
Во всех трех случаях   компланарны: в частности,  если  параллелен плоскости векторов  , что означает их компланарность. 

2.  Круговая  перестановка  сомножителей  в  смешанном  произведении  не изменяет  его  величины.  Перестановка  соседних  сомножителей  изменяет  его знак, не изменяя абсолютной величины: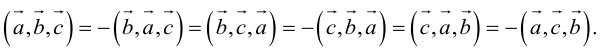  

Доказательство следует из формулы (2.9) и свойства 3 определителей, при этом круговая перестановка сомножителей соответствует двойной перемене строк в определителе, а потому оставляет его неизменным.  

3. В смешанном произведении векторное и скалярное произведения можно менять местами:
 

Доказательство:  из свойства 2 смешанного произведения и свойства 1 скалярного получим:

4.  Смешанное произведение линейно по каждому из трех сомножителей.  – линейность по первому сомножителю. 

Доказательство следует из формулы (2.9) и свойств определителей. 

Пример №14

Найти  объем  тетраэдра,  построенного  на  векторах   , и его высоту, перпендикулярную плоскости векторов . 
Объем тетраэдра в 6 раз меньше объема параллелепипеда, построенного на этих векторах, поэтому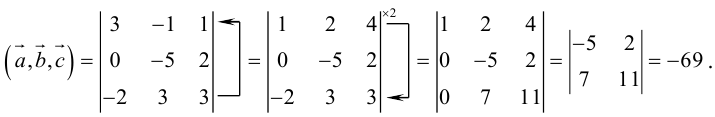
Отсюда (заметим, что – левая тройка, так как смешанное произведение отрицательно). 
Чтобы найти высоту, воспользуемся формулой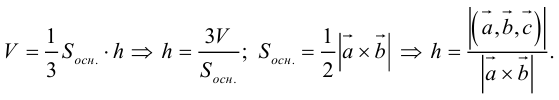    
По формуле (2.7)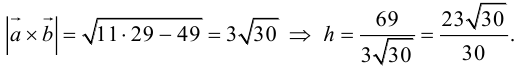

Лекции по предметам:

1. Математика
2. Алгебра
3. Линейная алгебра
4. Геометрия
5. Аналитическая геометрия
6. Высшая математика
7. Дискретная математика
8. Математический анализ
9. Теория вероятностей
10. Математическая статистика
11. Математическая логика

Почему мы используем $ijk$ для векторов?

Ответить

Проверено

157,8 тыс.+ просмотров

Подсказка: В этом вопросе нам задали вопрос о причине использования $ijk$ для векторов. Из основных представлений о векторах мы знаем, что $i,j,k$ — это единичные векторы вдоль осей x, y и z соответственно. В декартовой системе координат любой вектор обычно представляется в терминах его единичных векторов.

Полное пошаговое решение: Теперь, рассматривая вопрос, нам задали вопрос о причине использования $ijk$ для векторов.  Из основных представлений о векторах мы знаем, что $i,j,k$ — это единичные векторы вдоль осей x, y и z соответственно. В декартовой системе координат любой вектор обычно представляется в терминах его единичных векторов. Здесь единичные векторы представляют направление вектора. Мы знаем, что вектор — это физическая величина, имеющая как величину, так и направление. 9{2}}}$ . Обычно величина любого единичного вектора всегда равна единице. Вот почему для них придумано название единичного вектора. Единичный вектор также известен как вектор направления.

Примечание: При ответе на вопросы этого типа нас попросили обсудить всю концепцию, поэтому наша концепция должна быть ясной. Любой вектор можно представить в пространстве с помощью единичных векторов. Единичный вектор, лежащий вдоль направления $\vec{P}$, задается как $\hat{p}=\dfrac{{\vec{P}}}{\left| {\vec{P}} \right|}$ .

Недавно обновленные страницы

Если ab и c единичные векторы, то left ab2 right+bc2+ca2 математика класса 12 JEE_Main

Стержень AB длиной 4 единицы перемещается горизонтально, когда математика класса 11 JEE_Main

Оценить значение intlimits0pi cos 3xdx A 0 B 1 класс 12 математика JEE_Main

Что из следующего верно цианид с А Этиловый спирт класс 12 по химии JEE_Main

Если ab и c единичные векторы, то влево ab2 right+bc2+ca2 математика класса 12 JEE_Main

Стержень AB длиной 4 единицы перемещается горизонтально, когда математика класса 11 JEE_Main

Вычислить значение intlimits0pi cos 3xdx A 0 B 1 математика класса 12 JEE_Main

Что из следующего является правильным 1 nleft S чашка T справа класс 10 математика JEE_Main

Какова площадь треугольника с вершинами Aleft математика класса 11 JEE_Main

KCN легко реагирует с образованием цианида с A Этил спирт 12 класс химия JEE_Main

Актуальные сомнения

Студенты также читают

Почему мы дышим?

Почему мы болеем

Почему у нас два глаза?

How Much Water Do We Use

Векторное произведение – примеры и решения

В большинстве случаев встречаются три типа задач.

В задачах первого типа обычно заданы длины двух векторов и угол между ними, а нужно найти длину векторного произведения. В этом случае пользуются следующей формулойc→=a→·b→·sin∠a→,b→ .

Пример 1

Найдите длину векторного произведения векторов a→ и b→, если известноa→=3, b→=5, ∠a→,b→=π4.

Решение

С помощью определения длины векторного произведения векторов a→ и b→ решим данную задач: a→×b→=a→·b→·sin∠a→,b→=3·5·sinπ4=1522.

Ответ: 1522.

Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов a→=(ax; ay; az) и b→=(bx; by; bz).

Для такого типа задач, можно решить массу вариантов заданий. Например, могут быть заданы не координаты векторов  a→ и b→, а их разложения по координатным векторам вида b→=bx·i→ +by·j→+bz·k→ и c→=a→×b→=(ay·bz—az·by)·i→+(az·bx—ax·bz)·j→+(ax·by—ay·bx)·k→, или векторы a→ и b→ могут быть заданы координатами точек их начала и конца.

Рассмотрим следующие примеры.

Пример 2

В прямоугольной системе координат заданы два вектора a→=(2; 1; -3), b→=(; -1; 1). Найдите их векторное произведение.

Решение

По второму определению найдем векторное произведение двух векторов в заданных координатах:a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→==(1·1-(-3)·(-1))·i→+((-3)·-2·1)·j→+(2·(-1)-1·)·k→==-2i→-2j→-2k→.

Если записать векторное произведение через определитель матрицы, то решение данного примера выглядит следующим образом: a→×b→=i→j→k→axayazbxbybz=i→j→k→21-3-11=-2i→-2j→-2k→.

Ответ: a→×b→=-2i→-2j→-2k→.

Пример 3

Найдите длину векторного произведения векторов i→-j→ и i→+j→+k→, где i→, j→, k→ — орты прямоугольной декартовой системы координат.

Решение

Для начала найдем координаты заданного векторного произведения i→-j→×i→+j→+k→ в данной прямоугольной системе координат.

Известно, что векторы i→-j→ и i→+j→+k→ имеют координаты (1; -1; )  и (1; 1; 1) соответственно. Найдем длину векторного произведения при помощи определителя матрицы, тогда имеем i→-j→×i→+j→+k→=i→j→k→1-1111=-i→-j→+2k→.

Следовательно, векторное произведение i→-j→×i→+j→+k→ имеет координаты (-1; -1; 2) в заданной системе координат.

Длину векторного произведения найдем по формуле (см. в разделе нахождение длины вектора): i→-j→×i→+j→+k→=-12+-12+22=6.

Ответ: i→-j→×i→+j→+k→=6..

Пример 4

В прямоугольной декартовой системе координат заданы координаты трех точек A(1,,1), B(,2,3), C(1,4,2) . Найдите какой-нибудь вектор, перпендикулярный AB→ и AC→ одновременно.

Решение

Векторы  AB→ и AC→ имеют следующие координаты (-1; 2; 2) и (; 4; 1) соответственно. Найдя векторное произведение векторов AB→ и AC→, очевидно, что оно является перпендикулярным вектором по определению и к  AB→​​​​​ и к AC→, то есть, является решением нашей задачи. Найдем его AB→×AC→=i→j→k→-12241=-6i→+j→-4k→.

Ответ: -6i→+j→-4k→. — один из перпендикулярных векторов.

Задачи третьего типа ориентированы на использование свойств векторного произведения векторов. После применения которых, будем получать решение заданной задачи.

Пример 5

Векторы  a→ и b→ перпендикулярны и их длины равны соответственно 3 и 4. Найдите длину векторного произведения 3·a→-b→×a→-2·b→=3·a→×a→-2·b→+-b→×a→-2·b→==3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→.

Решение

По свойству дистрибутивности векторного произведения мы можем записать 3·a→-b→×a→-2·b→=3·a→×a→-2·b→+-b→×a→-2·b→==3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→

По свойству ассоциативности вынесем числовые коэффициенты за знак векторных произведений в последнем выражении: 3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→==3·a→×a→+3·(-2)·a→×b→+(-1)·b→×a→+(-1)·(-2)·b→×b→==3·a→×a→-6·a→×b→-b→×a→+2·b→×b→

Векторные произведения a→×a→ и b→×b→ равны 0, так как a→×a→=a→·a→·sin= и b→×b→=b→·b→·sin=, тогда 3·a→×a→-6·a→×b→-b→×a→+2·b→×b→=-6·a→×b→-b→×a→..

Из антикоммутативности векторного произведения следует -6·a→×b→-b→×a→=-6·a→×b→-(-1)·a→×b→=-5·a→×b→..

Воспользовавшись свойствами векторного произведения, получаем равенство 3·a→-b→×a→-2·b→==-5·a→×b→.

По условию векторы  a→ и b→ перпендикулярны, то есть угол между ними равен π2. Теперь остается лишь подставить найденные значения в соответствующие формулы: 3·a→-b→×a→-2·b→=-5·a→×b→==5·a→×b→=5·a→·b→·sin(a→,b→)=5·3·4·sinπ2=60.

Ответ: 3·a→-b→×a→-2·b→=60.

Смешанное произведение векторов

Смешанное произведение применяется довольно редко, поэтому и примеров задач не много.

Практически вся информация сводится к следующим данным:

• главному определению;
• геометрическому смыслу;
• рабочие формулы.

Важно

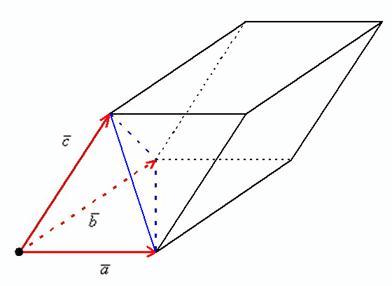
Смешанным произведение нескольких векторов, будет называться произведение трёх характерных векторных значений:

Смешанное произведение трех векторов \ и некомпланарных векторов \, которые берутся в определенном порядке, будет называется объём геометрического параллелепипеда.

Данная геометрическая фигура построена на заданных векторах, которые отражены с положительным значением.

 Если базисное значение векторов  \ имеет правое направление , когда отрицательный знак, то  базис векторов \ имеет  левое направление.

Все характеристики подробно изображены на рисунке.

Коллинеарные и компланарные векторы. Основные определения

Определение 1

Компланарные вектора — это вектор или несколько векторов, которые расположены на одной плоскости либо располагаются параллельно ей.

Компланарность характерна всегда двум любым, на выбор, векторам. Так как всегда можно вычистить плоскость, которой будет параллельны произвольные вектора.

Выведем основное правило признака копланарности вектора.

При условии, что два вектора a и b не характеризуются как календарные, а для вектора с свойственны только одна пара чисел x и y. c=xa+yb. Если соблюдаются данные условия, то перечисленные векторы можно назвать компланарными.

Обратное утверждение компланарности.

Когда вектора a , b , c — компланарны, при этом a , b не относятся к коллинеарным. можно вектор c разложить по двум любым векторам, только одним способом.

Определение 2

Коллинеарность векторов это — принцип соотношения параллельности векторов. Два вектора с нулевым значением, будут иметь коллинеарность, при условии, что они находятся лежат на параллельной прямой или на одной плоскости с ней.

Векторные уравнения плоскости и прямой.

Параметрическое уравнение плоскости утверждает, что точка \(M\) лежит на плоскости тогда и только тогда, когда разность ее радиус-вектора и радиус-вектора начальной точки \(M_\) компланарна направляющим векторам \(\boldsymbol

\) и \(\boldsymbol\). Эту компланарность можно выразить и равенством $$ (\boldsymbol-\boldsymbol_, \boldsymbol

, \boldsymbol) = 0.\label$$ Вектор \(\boldsymbol = [\boldsymbol

, \boldsymbol]\) — ненулевой вектор, перпендикулярный плоскости. Используя его, мы можем записать уравнение \eqref в виде $$ (\boldsymbol-\boldsymbol_, \boldsymbol) = 0.\label$$

Уравнения \eqref и \eqref называют векторными уравнениями плоскости. Им можно придать форму, в которую не входит радиус-вектор начальной точки. Например, положив в \eqref \(D = -(\boldsymbol_, \boldsymbol)\), получим $$ (\boldsymbol, \boldsymbol)+D = 0.\label$$

Для прямой на плоскости можно также написать векторные уравнения, аналогичные \eqref и \eqref, $$ (\boldsymbol-\boldsymbol_, \boldsymbol) = 0\ \mbox\ (\boldsymbol, \boldsymbol)+C = 0.\nonumber $$ Первое из них выражает тот факт, что вектор \(\boldsymbol-\boldsymbol_\) перпендикулярен ненулевому вектору \(\boldsymbol\), перпендикулярному направляющему вектору \(\boldsymbol\), и потому коллинеарен \(\boldsymbol\).

Пусть \(x, y, z\) — компоненты вектора \(\boldsymbol\) в общей декартовой системе координат. Тогда скалярное произведение \((\boldsymbol-\boldsymbol_, \boldsymbol)\) при \(\boldsymbol \neq 0\) записывается линейным многочленом \(Ax+By+Cz+D\), где \((A^+B^+C^ \neq 0)\).

Обратно, для любого линейного многочлена найдутся такие векторы \(\boldsymbol_\) и \(\boldsymbol \neq 0\), что в заданной общей декартовой системе координат \(Ax+By+Cz+D = (\boldsymbol-\boldsymbol_, \boldsymbol)\).

Первая часть предложения очевидна: подставим разложение вектора \(\boldsymbol\) по базису в данное скалярное произведение: $$ (x\boldsymbol_+y\boldsymbol_+z\boldsymbol_-\boldsymbol_, \boldsymbol),\nonumber $$ раскроем скобки и получим многочлен \(Ax+By+Cz+D\), в котором \(D = -(\boldsymbol_, \boldsymbol)\) и $$ A = (\boldsymbol_, \boldsymbol),\ B = (\boldsymbol_, \boldsymbol),\ C = (\boldsymbol_, \boldsymbol)\label$$ \(A\), \(B\) и \(C\) одновременно не равны нулю, так как ненулевой вектор \(\boldsymbol\) не может быть ортогонален всем векторам базиса.

Для доказательства обратного утверждения найдем сначала вектор \(\boldsymbol\) из равенств \eqref, считая \(A\), \(B\) и \(C\) заданными. Из ранее доказанного утверждения 10 следует, что $$ \boldsymbol = \frac_, \boldsymbol_]>_, \boldsymbol_, \boldsymbol_)>+\frac_, \boldsymbol_]>_, \boldsymbol_, \boldsymbol_)>+\frac_, \boldsymbol_]>_, \boldsymbol_, \boldsymbol_)>.\label$$

Вектор \(\boldsymbol_\) должен удовлетворять условию \(D = -(\boldsymbol_, \boldsymbol)\). Один из таких векторов можно найти в виде \(\boldsymbol_ = \lambda \boldsymbol\). Подставляя, видим, что \(-\lambda(\boldsymbol, \boldsymbol) = D\), откуда \(\boldsymbol_ = -D\boldsymbol/|\boldsymbol|^\).

Итак, мы нашли векторы \(\boldsymbol\) и \(\boldsymbol_\) такие, что линейный многочлен записывается в виде $$ x(\boldsymbol_, \boldsymbol)+y(\boldsymbol_, \boldsymbol)+z(\boldsymbol_, \boldsymbol)-(\boldsymbol_, \boldsymbol),\nonumber $$ который совпадает с требуемым \((\boldsymbol-\boldsymbol_, \boldsymbol)\).

Если система координат декартова прямоугольная, то вектор с компонентами \(A\), \(B\), \(C\) является нормальным вектором для плоскости с уравнением \(Ax+By+Cz+D = 0\).

Это сразу вытекает из формул \eqref и доказанного ранее утверждения о нахождении компонент в ортогональном базисе.

Любые два неколлинеарных вектора, удовлетворяющие уравнению \eqref, можно принять за направляющие векторы плоскости.

Утверждение 5 нетрудно доказать и непосредственно, рассматривая координаты вектора, параллельного плоскости, как разности соответствующих координат двух точек, лежащих в плоскости.

Все, сказанное о плоскостях, почти без изменений может быть сказано и о прямых на плоскости. В частности, верно следующее утверждение.

Действительно, \(\alpha_, \alpha_\), должны быть пропорциональны компонентам — \(B\), \(A\) направляющего вектора прямой.

Смешанное произведение векторов в координатах

Для данного способа определения произведения векторов, используется сугубо алгебраический метод.

Перечень смешанных векторов: \, которые непосредственно заданы в координатной системе данных  \  для правого направления, следует выражать характерной формулой, виде матрицы:

Определение

Ориентация базиса – это его стандартная ориентация, для которой решаются практически все задачи.

С практической точки зрения стоит отметить следующие важные моменты:

• для всего векторного произведения, координатные данные векторов следует изображать в конкретный определитель в особо строгом порядке.
• когда в любом смешанном произведении \ выбрать несколько векторов, затем переставить их местами, следовательно нужно переставить и все характерные строки определителя.
• при перестановке строк в количестве двух штук, соответствующие строки изменяют знак на противоположный.
• при перемене местами любых векторов, для смешанного произведения будет характерно изменение знака на противоположный.

Соответственно, все координаты векторов не всегда нужно записывать в виде строк. Также они могут изображаться как таблица: слева направо, и обязательно, в строгом порядке.

Основное значение главного определителя при этом изменяться не будет: компланарность векторов также имеет огромное значение в данном случае.

Пример 1

Даны следующие значения векторов \.

Необходимо определить:

• смешанное векторное произведение;
• значение объема параллелепипеда, который построен на векторах \;
• значение объёма геометрической фигуры тетраэдра, который также построен на векторах \.

Процесс решения заключается в следующем

1. Применяя формулу для смешанного произведения вычисляем неизвестную:

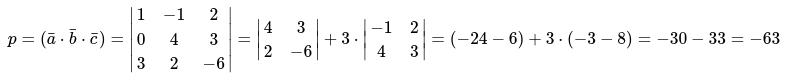
Значение определителя раскрыто по первому столбцу

2. Определение значения объёма параллелепипеда, который построен на векторах \, равняется модулю смешанного векторного произведения:

3. Определяем значение объема тетраэдра, который построен на заданных векторах:

Ответ:

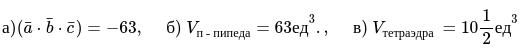
Пример 2

Определить значение объема, которое характерно для треугольной пирамиды. Применяя все известные ее вершины: A(-2 ;-2 ; 0), B(0 ; 4 ;-1), C(1 ; 2 ; 1), D(-13 ; 8 ; 11)

Решение: Для простоты выполнения, рекомендуется выполнять схематический рисунок геометрической пирамиды, это необходимо для более понятного процесса решения.

Для начал определяются значения векторов, по исходным данным:

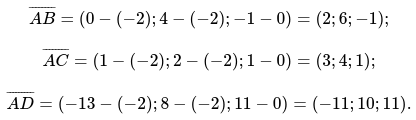
Следующим действием произведение векторов смешанного типа.

\

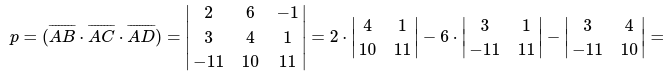Выполним расчет для треугольной пирамиды ABCD:

Ответ задачи: \

Пример 3

Определить объём заданной пирамиды, с известными вершинами: \

Для начала определим значения векторов

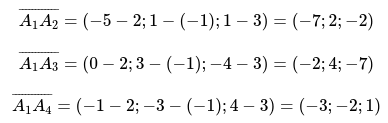
Смешанное произведение определим по формуле:

\

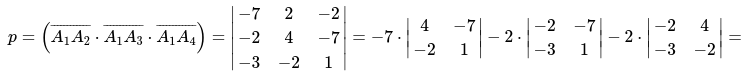Применяя формулу из геометрии определим объем пирамиды \

\

\

Правые и левые тройки векторов

Для того, чтобы получить векторное произведение двух векторов, необходимо, чтобы:

1) векторы были не коллинеарны;

2) векторы были взяты в определённом порядке.

Определённый порядок связан с понятием упорядоченных троек векторов. В этой тройке два вектора —
перемножаемые векторы, а третий — векторное произведение этих векторов.

Определение 1. Три вектора называются упорядоченной тройкой (или просто тройкой), если указано,
какой из этих векторов является первым, какой — вторым и какой — третьим.

При записи тройки векторов мы всегда будем располагать эти векторы в порядке их следования.
Так, запись означает, что первым
элементом тройки является вектор , вторым —
вектор и третьим — вектор .

Определение 2. Тройка некомпланарных векторов
называется правой (левой), если выполнено одно из следующих трёх условий:

1. если, будучи приведены к общему началу, эти векторы располагаются так, как могут быть расположены
соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки;

2. если после приведения к общему началу вектор располагается по ту
сторону от плоскости, определяемой векторами и ,
откуда кратчайший поворот от к
представляется совершающимся против часовой стрелки (по часовой стрелке);

3. если, находясь внутри телесного угла, образованного приведёнными к общему началу векторами , , ,
мы видим поворот от к и от него к
совершающимся
против часовой стрелки (по часовой стрелке).

Условия 1, 2 и 3 эквивалентны между собой. С помощью каждого из приведённых условий можно
убедиться в том, что тройка , изображённая
на рис. 1, является правой, а тройка , изображённая на
рис. 2, является левой.

Замечание. Понятие правой и левой тройки теряет смысл для компланарных векторов.

Если две тройки векторов либо обе являются правыми, либо обе являются левыми, то принято считать, что эти тройки
одной ориентации. В противном случае — две тройки противоположной ориентации.

Всего из трёх векторов , и
можно составить следующие шесть троек:

;  ;    (1)

;  ;    (2)

С помощью условия 3 определения 2 легко проверить, что все три тройки (1) той же ориентации, что и тройка
, а все три тройки (2) имеют ориентацию, противоположную
.

Определение 3. Аффинная или декартова система координат называется правой (левой), если три базисных вектора
образуют правую (левую) тройку.

Главные свойства векторного произведения

Для некоторых произвольных векторов \ и произвольного значения числа \, являются справедливыми следующие главные свойства:

1. \=\overline{0}\] — данное свойство обычно не выделяют. Однако именно оно является важным моментом процессе решения векторных задач.
2. \=-\] – это свойство часто называют анти коммуникативным. Иными словами, порядок векторов может иметь разное направление и значение.
3. \=\lambda, \quad=\lambda\] – суммарные и ассоциативные законы для векторных произведений. Константа выносится за пределы векторного произведения в координатной оси.
4. \=+, \quad=+\] – распределительные или действующие законы векторного произведения. Для решения главным моментом является умение правильно раскрывать значение в скобках.

Некоторые приложения векторного произведения Установление коллинеарности векторов

Если , то (и наоборот), т. е.

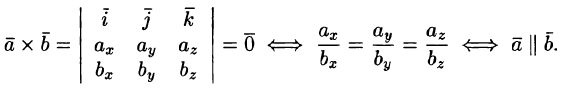
Определение момента силы относительно точки

Пусть в точке А приложена сила и пусть О — некоторая точка пространства (см. рис. 20).

Из физики известно, что моментом силы относительно точки О называется вектор , который проходит через точку О и:

1) перпендикулярен плоскости, проходящей через точки О, А, В;

2) численно равен произведению силы на плечо

3) образует правую тройку с векторами . Стало быть,

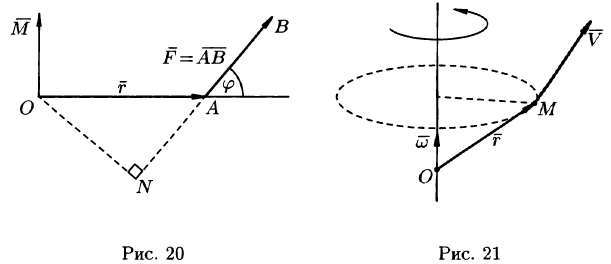
Нахождение линейной скорости вращения

Скорость точки М твердого тела, вращающегося с угловой скоростью вокруг неподвижной оси, определяется формулой Эйлера , где , где О — некоторая неподвижная точка оси (см. рис. 21).

Vectors

Contents

• Entering vectors in MATLAB
• Комментарии к стилю
• Векторная арифметика
• Скалярное произведение
• Перекрестное произведение

Ввод векторов в MATLAB

столбцы). Итак, чтобы войти в векторы A = -3 I — 4 J — K , B = 6 I + 2 J + 3 K и U = x J + 3 K и U = x J + 3 K и U = x J + 3 K и U = x J + 3 K и U = x . я + у j + z k введите

 a = 
 

а =

    -3 -4 -1

 

 б = 
 

б =

     6 2 3

 

и

 символов x y z
и = 
 

ты =
 

 
 

Команда syms необходима, чтобы сообщить MATLAB, что x,y,z являются символическими. Если вы забудете это сделать, вы получите сообщение об ошибке, говорящее о том, что у вас есть неопределенная функция или переменная. 92

Вы можете складывать и вычитать их, а также умножать на скаляры.

 а + б
 

ответ =

     3 -2 2

 

 5*а
 

ответ =

   -15 -20 -5

 

2 Вектор на плоскости и в пространстве

Вектором
называется направленный отрезок с началом и концом, изображаемым на
рисунке стрелкой. Произвольная точка пространства может считаться
нулевым вектором. Нулевой вектор не имеет конкретного направления,
так как начало и конец совпадают, поэтому ему можно придать любое
направление.

Длина
(модуль) ненулевого вектора

— это длина отрезка AB, которая
обозначается

.
Длина вектора

обозначается

.
Нулевой вектор имеет длину равную нулю

= 0.

Коллинеарными
называются ненулевые векторы, лежащие на одной прямой или на
параллельных прямых. На рисунках ниже изображены коллинеарные векторы

,

.

На
рисунке ниже также изображены коллинеарные векторы

,
и
.

Нулевой
вектор коллинеарен любому вектору.

Нулевой
вектор сонаправлен с любым вектором.

Равными
называются сонаправленные векторы равной длины. На рисунке ниже
изображены равные векторы

=
.

Противоположными
называются два ненулевых противоположно направленных вектора равной
длины. Вектор —

является противоположным вектору

Противоположные
векторы противоположно направленные и равны по модулю. Если даны
точки A и B,
то следующие векторы противоположные

Равные
по модулю равные или противоположные, или нулевые векторы.

Многие
физические величины являются векторными величинами: сила, скорость,
электрическое поле и т.д.

Если
не задана точка приложения (начала) вектора, то она выбирается
произвольно.

Если
в точку O поместить начало вектора, то
считается, что вектор отложен от точки O.
Из любой точки можно отложить единственный вектор, равный данному
вектору.