Смешанное произведение векторов: что это, его свойства и как найти по формуле

Определитель третьего порядка

Отныне и впредь, когда ты будешь иметь дело с методом координат на плоскости, тебе очень часто будут встречаться эти самые определители.

Что же такое определитель третьего порядка? Как ни странно, это всего-навсего число. Осталось понять, какое конкретно число мы будем сопоставлять с определителем.

Давай вначале запишем определитель третьего порядка в более общем виде:

Причем под первым индеком $ \displaystyle i$ мы понимаем номер строки, а под индеком $ \displaystyle j$ – номер столбца.

Например, $ {{a}_{23}}$ означает, что данное число стоит на пересечении второй строки и третьего столбца.

Давай поставим следующий вопрос: каким именно образом мы будем вычислять такой определитель?

То есть, какое конкретно число мы будем ему сопоставлять?

Для определителя именно третьего порядка есть эвристическое (наглядное) правило треугольника оно выглядит следующим образом:

Как его читать? А понимать его надо следующим образом: мы составляем два выражения:

Произведение элементов главной диагонали (с верхнего левого угла до нижнего правого) $ \displaystyle +$ произведение элементов, образующих первый треугольник «перпендикулярный» главной диагонали $ \displaystyle +$ произведение элементов, образующих второй треугольник «перпендикулярный» главной диагонали;
Произведение элементов побочной диагонали (с верхнего правого угла до нижнего левого) $ \displaystyle +$ произведение элементов, образующих первый треугольник «перпендикулярный» побочной диагонали $ \displaystyle +$ произведение элементов, образующих второй треугольник «перпендикулярный» побочной диагонали;
Тогда определитель равен разности значений, полученных на шаге $ \displaystyle 1$ и $ \displaystyle 2$.

Если записать все это цифрами, то мы получим следующее выражение:

$ \left| {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\{{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}\end{array}} \right| = $$ = {a_{11}}{a_{22}}{a_{33}} + {a_{12}}{a_{23}}{a_{31}} + {a_{21}}{a_{32}}{a_{13}} — \left( {{a_{13}}{a_{22}}{a_{31}} + {a_{23}}{a_{32}}{a_{11}} + {a_{21}}{a_{12}}{a_{33}}} \right)$Тем не менее, запоминать способ вычисления в таком виде не нужно, достаточно в голове просто держать треугольники и саму идею, что с чем складывается и что из чего затем вычитается).

Длина отрезка. Расстояние между точками: онлайн-калькулятор

Чтобы найти расстояние между точками (длину отрезка) онлайн, необходимо:

Задать размерность (плоскость или пространство).
Ввести в поля координаты точек.
Нажать «рассчитать».

Как найти длину отрезка (расстояние между точками) с помощью онлайн-калькулятора

Рассмотрим пример, наглядно демонстрирующий работу с онлайн-калькулятором. Найдем длину произвольного отрезка, начальная и конечная точки которого имеют координаты (1;4) и (3;0). Для этого:

Выберем размерность (2 или 3). Калькулятор позволяет задать отрезок соответственно на плоскости, или в пространстве. В нашем конкретном примере выберем плоскость (2):
Введем в пустые поля координаты начальной и конечной точек отрезка:
После ввода координат остается нажать «Рассчитать» и получить ответ с решением:

Материалы, которые помогут вам лучше разобраться в теме:

Середина отрезка
Каноническое уравнение прямой проходящей через две точки
Параметрическое Уравнение прямой проходящей через две точки
Расстояние от точки до прямой на плоскости
Уравнение плоскости (координаты трех точек)
Уравнение плоскости (координаты вектора нормали и точки)
Точка пересечения прямых (с угловыми коэффициентами)
Расстояние от точки до прямой в пространстве
Расстояние от точки до плоскости
Расстояние между плоскостями
Угол между плоскостями
Угол между прямой и плоскостью

Расстояние между точками онлайн

Для нахождения длины отрезка по координатам существует формула. Для отрезка AB в трехмерном пространстве она имеет вид:

d = x b — x a 2 + y b — y a 2 + z b — z a 2

Даже если вы забыли данную формулу, расстояние между точками всегда можно найти по координатам онлайн. Калькулятор не только предоставляет правильный ответ, но и подробно расписывает решение.

Онлайн-калькулятор нахождения длины отрезка по координатам будет полезен школьникам и студентам в самостоятельной подготовке, а также преподавателям и всем любителям математики.

1.3. Умножение матриц

Матрицы можно перемножать, но только в том случае, когда они имеют
соответствующие размерности. Почему это так, будет ясно из определения.
Произведением матрицы A, размерностью I×K, и
матрицы B, размерностью K×J, называется
матрица C, размерностью I×J, элементами
которой являются числа

Таким образом для произведения AB необходимо, чтобы число
столбцов в левой матрице A было равно числу строк в правой
матрице B. Пример произведения матриц —

Рис.6 Произведение матриц

Правило перемножения матриц можно сформулировать так. Для того, чтобы найти
элемент матрицы C, стоящий на пересечении i-ой строки
и j-ого столбца (c_ij) надо поэлементно перемножить
i-ую строку первой матрицы A на j-ый столбец
второй матрицы B и сложить все результаты. Так в показанном
примере, элемент из третьей строки и второго столбца, получается как сумма
поэлементных произведений третьей строки A и второго столбца
B

Рис.7 Элемент произведения матриц

Произведение матриц зависит от порядка, т.е. AB ≠
BA, хотя бы по соображениям размерности. Говорят, что оно
некоммутативно. Однако произведение матриц ассоциативно. Это означает, что
ABC = (AB)C =
A(BC). Кроме того, оно еще и дистрибутивно,
т.е. A(B+C) =
AB+AC. Очевидно, что AO =
O.

Вычисление нормальных векторов для плоскостей

Нормальные векторы — это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.

Другими словами, нормаль — это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение — правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом — хоть прямой, хоть вектором.

Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).

Итак, плоскость тоже можно успешно заменить вектором — той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:

Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A₁, B и C₁, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;

Аналогично, для точек B = (1; 0; 0) и C₁ = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;

Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B:
B = − 1 − A − C = − 1 + 1 + 1 = 1.

Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).

В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A₁ и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;

Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;

Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).

Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т.е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и правильности ответа.

Выбор системы координат

Ну вот, теперь у нас есть весь необходимый фундамент знаний, чтобы решать сложные стереометрические задачи по геометрии.

Однако прежде чем приступать непосредственно к примерам и алгоритмам их решения, я считаю, что будет полезно остановиться еще вот на каком вопросе: как именно выбирать систему координат для той или иной фигуры.

Ведь именно выбор взаимного расположения системы координат и фигуры в пространстве в конечном счете определит, насколько громоздкими будут вычисления.

Я напомню, что в этом разделе мы рассматриваем следующие фигуры:

куб;
Прямоугольный параллелепипед;
Прямая призма (треугольная, шестиугольная…);
Пирамида (треугольная, четырехугольная);
Тетраэдр (одно и то же, что и треугольная пирамида).

2.1. Системы линейных уравнений

Пусть A — матрица размером I×J, а
b — вектор размерности J. Рассмотрим уравнение

Ax = b

относительно вектора
x, размерности I. По сути — это система из I
линейных уравнений с J неизвестными
x₁,…,x_J. Решение существует в том, и
только в том случае, когда

rank(A) = rank(B) =
R,

где B — это расширенная матрица размерности
I×(J+1), состоящая из матрицы A, дополненной
столбцом b, B = (A
b). В противном случае уравнения несовместны.

Если R = I = J, то решение единственно

x = A−1b.

Если
R < I, то существует множество различных решений, которые
можно выразить через линейную комбинацию J−R векторов. Система
однородных уравнений Ax = с квадратной
матрицей A (N×N) имеет нетривиальное решение
(x ≠ ) тогда и только тогда, когда
det(A) = 0. Если R =
rank(A)<N, то существуют N−R
линейно независимых решений.

Понятие смешанного произведения векторов

Определение 3

Смешанным произведением векторов $overline{α}$, $overline{β}$ и $overline{γ}$ будем называть такой скаляр (или число), которое будет равняться скалярному произведению первого вектора $overline{α}$ на вектор векторного произведения $overline{β}хoverline{γ}$ двух других векторов.

Обозначение: $(overline{α},overline{β},overline{γ})$.

Математически это выглядит следующим образом:

$(overline{α},overline{β},overline{γ})=overline{α}cdot (overline{β}хoverline{γ})$

Очевидно, что смешанное произведение будет равняться нулю в двух случаях:

Если длина одного или нескольких векторов равняется нулю.
Если эти векторы будут являться компланарными.

Пример 1

Найти значение смешанного произведения векторов $overline{α}$, $overline{β}$ и $overline{γ}$, которые имеют координаты $(0,0,5)$, $(0,4,0)$ и $(3,0,0)$, соответственно.

Решение.

Из определений 1, и 3 будем получать

$(overline{α},overline{β},overline{γ})=overline{α}cdot (overline{β}хoverline{γ})=|overline{a}||overline{β}хoverline{γ}|cos∠(overline{α},overline{β}хoverline{γ})$

Изобразим эти векторы в декартовом координатном пространстве (рис. 2):

Найдем вначале длину вектора векторного произведения векторов $overline{β}$ и $overline{γ}$

Видим, что эти векторы лежат на осях $Ox$ и $Oy$, соответственно. Следовательно, угол между ними будет равняться $90^0$. Найдем длины этих векторов:

$|overline{β}|=sqrt{0+16+0}=4$

$|overline{γ}|=sqrt{9+0+0}=3$

Тогда, по определению 2, получим

$|overline{β}хoverline{γ}|=|overline{α}||overline{β}|sin90^circ=4cdot 3cdot 1=12$

Из 3 части определения 2 очевидно, что вектор $overline{β}хoverline{γ}$ принадлежит оси $Oz$ и направлен в туже сторону, что и сама ось, следовательно, угол между векторами $overline{α}$ и $overline{β}хoverline{γ}$ равняется $0^circ$.

Длина вектора $overline{α}$

$|overline{α}|=sqrt{0+0+25}=5$

Получим

$(overline{α},overline{β},overline{γ})=|overline{a}||overline{β}хoverline{γ}|cos∠(overline{α},overline{β}хoverline{γ})=5cdot 12cdot cos0^circ=60$

Ответ: $60$.

Векторное произведение

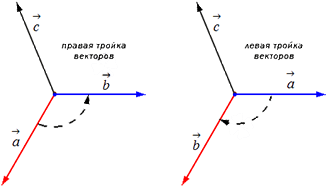
Для того чтобы дать правильное определение векторного произведения, необходимо разобраться в следующем моменте: рассмотреть вопрос, касающийся ориентации всей упорядоченной группы векторов. Для всего пространства на координатной плоскости.

Нужно отложить все три вектора от одной конкретной точки в системе. Ориентация для векторов может быть двух направлений:

правая;
левая.

Направление непосредственно зависит от направления самого вектора. Именно в каком направление будет осуществляться самый кратчайший поворот от двух векторов, а и b от конца третьего вектора с. При условии, что самый короткий поворот против часовой стрелки, тогда все три вектора будут именоваться – правыми.

Соответственно левыми будут называться вектора, движение которых происходит по направлению часовой стрелки.

Определение

Произведение векторов неколлинеарных векторов \, которые взятых в определённом порядке – это любой принятый вектор \, у которого длина равняется площади геометрической фигуры параллелограмм. Именно он построен на основании данных векторов; вектор \ ортогонален двум другим векторам \, и направлен так, что \ являются ориентированы в правом направлении.

Следовательно, можно выделить следующие основные моменты:

1. Заданные векторы, которые обозначены линиями красного цвета, и основываясь на определение являются не коллинеарными

2. Векторы \ приняты в заданном порядке: произведение \_{-}\]

Окончательный результат выражен как: \\], обозначенный синим цветом.

Если вектора перемножить в обратном порядке, получится равный по всей длине и противоположный по направлению вектор \\].

Следовательно: \=-\]

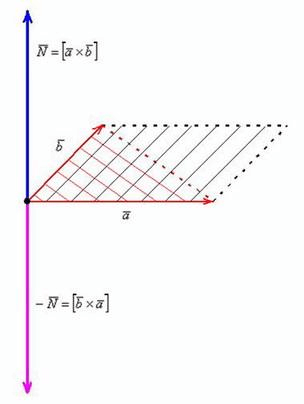
3. Геометрический смыл векторного произведения.

Величина длины синего вектора \\] (следовательно это справедливо и для красного вектора \\]) будет равна площади параллелограмма. Который построен на векторах \. На схеме, данная фигура изображена штриховкой черного цвета. чёрным цветом.

Исходя из вышесказанного, справедливой будет формула определения длины для векторного произведения:

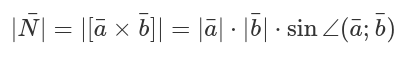
Данная формула отражает длину вектора а не его самого \. Для задач геометрии площадь параллелограмма зачастую определяют через главное понятие произведения векторов:

Выведем следующую формулу. Диагональ у параллелограмма (красная пунктирная линия) делит фигуру два равных треугольника.

Из этого следует, что площадь треугольника, который построен на векторах \, определяется по формуле:

4. Стоит помнить, что вектор \ ортогонален векторам \, иными словами \.

1.13. Ранг матрицы

Рассмотрим набор из K векторов x₁,
x₂,…,x_K размерности
N. Рангом этой системы векторов называется максимальное число
линейно-независимых векторов. Например в наборе

имеются только два линейно независимых вектора, например
x₁ и x₂, поэтому ее ранг
равен 2.

Очевидно, что если векторов в наборе больше, чем их размерность
(K>N), то они обязательно линейно зависимы.

Рангом
матрицы (обозначается rank(A)) называется ранг системы
векторов, из которых она состоит. Хотя любую матрицу можно представить двумя
способами (векторы столбцы или строки), это не влияет на величину ранга, т.к.

rank(A) = rank(At).

Вычисление смешанного произведения по координатам векторов

Из определения 1 сразу же вытекает и способ нахождения смешанного произведения для трех данных векторов. Но существует еще способ нахождения с помощью координат данных нам векторов.

Пусть нам даны векторы $overline{α}$, $overline{β}$ и $overline{γ}$, которые будут иметь координаты $(α_1,α_2,α_3)$, $(β_1,β_2,β_3)$ и $(γ_1,γ_2,γ_3)$, соответственно. Тогда значение смешанного произведения можно найти по следующей формуле:

$(overline{α},overline{β},overline{γ})=begin{vmatrix}α_1&α_2&α_3\β_1&β_2&β_3\γ_1&γ_2&γ_3end{vmatrix}$

Иначе, получим

$overline{α}хoverline{β}=α_1 β_2 γ_3+α_3 β_1 γ_2+α_2 β_3 γ_1-α_3 β_2 γ_1-α_2 β_1 γ_3-α_1 β_3 γ_2$

Пример 2

Найти значение смешанного произведения векторов $overline{α}$, $overline{β}$ и $overline{γ}$ с координатами $(1,1,0)$, $(0,3,3)$ и $(-1,2,6)$.

Решение.

Воспользуемся формулой, приведенной выше. Получим

$(overline{α},overline{β},overline{γ})=begin{vmatrix}1&1&0\0&3&3\-1&2&6end{vmatrix}=18+(-3)+0-0-6-0=18-9=9$

Ответ: $9$.

Примеры решения

Для решения некоторых категорий задач, необходимо пользоваться тригонометрической таблицей. Для определения углов функций.

Пример 1:

Необходимо определить длину векторного произведения двух векторов \, , если:

Определить площадь параллелограмма, который построен на основании векторов \, если:

По условию задачи необходимо вычислить длину векторного произведения. По следующей формуле:

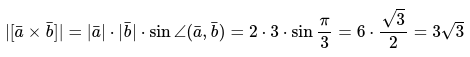
Ответ:

В ответе обязательно следует указывать единицы измерения, так как определится длина.

Из условия задачи нужно определить площадь фигуры параллелограмм, который построен на векторах \.

Площадь равняется значению длины векторного произведения:

Ответ:

Пример 2:

Определить площадь геометрической фигуры треугольник, который построен на векторах \, , если:

Для решения задачи применим соответствующую формулу и вспомним все преобразования, которые необходимы для определения площади.

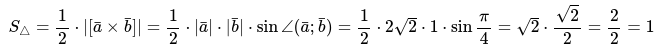
Ответ:

Пример 3:

Найти:

Решение: По условию требуется определить длину векторного произведения:

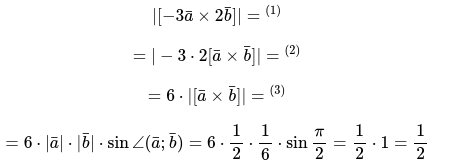
Алгоритм решения:

вынести за пределы скобок векторного произведения все константы, согласно ассоциативного закона.

затем выносим значение константы за пределы модуля; при этом модуль изменят отрицательный знак на положительный.

Ответ:

Пример 4:

Необходимо определить значение площади треугольника.

Для этого задано в задаче следующие данные:

, если:

Алгоритм решения задачи:

Площадь треугольника определяется по уже известной формуле:

Данный алгоритм стандартный и частично имеет схожесть с другими примерами.

Решение для удобства, необходимо разделить на три этапа:

Этап 1:

Нужно правильно выразим произведение векторов: \\] через определение векторного произведения \\].

Иными словами, выражение вектора через вектор.

Для этого сформулируем и запишем следующее:

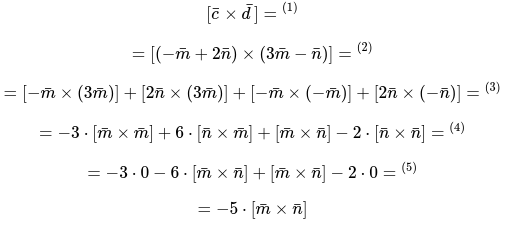
подставляем в формулу соответствующие выражения векторов \.

используя определённые законы, нужно раскрыть скобки по характерным правилам умножения числовых многочленов.

применяя ассоциативные векторные законы, можно вынести все константы за скобки и пределы векторных произведений.

Первое и последнее выражение равно нулевому значению или нулевому вектору, исходя из принятого свойства: \=\overline{0}\].

Для второго слагаемого применяется свойство анти коммутативности и выглядит следующим образом: \=-6 \cdot\]

— приведение подобных слагаемых.

По результатам вычисления заданный вектор получился выражен через вектор. Этого и требовалось доказать:\=-5 \cdot\]

Этап 2:

На втором этапе определяется длина заданного векторного произведения.

Приведенное действие напрямую напоминает задачу №3:

Этап 3:

Применяя все известные данные и формулы, можно определить площадь треугольника:

Ответ

Пример 5:

Определить векторное произведение, применяя все заданные значения векторов:

\|\], если:

Необходимо выразить вектор \\] через другой вектор \\]:

Используя все данные и алгоритм решения можно составить формулу и записать следующее выражение подставляя числа:

Окончательным действием будет определение произведения векторов, поэтапно подставляя все числовые значения:

Ответ задачи: \|=4 \text { ед }\]

Коллинеарные и компланарные векторы. Основные определения

Определение 1

Компланарные вектора — это вектор или несколько векторов, которые расположены на одной плоскости либо располагаются параллельно ей.

Компланарность характерна всегда двум любым, на выбор, векторам. Так как всегда можно вычистить плоскость, которой будет параллельны произвольные вектора.

Выведем основное правило признака копланарности вектора.

При условии, что два вектора a и b не характеризуются как календарные, а для вектора с свойственны только одна пара чисел x и y. c=xa+yb. Если соблюдаются данные условия, то перечисленные векторы можно назвать компланарными.

Обратное утверждение компланарности.

Когда вектора a , b , c — компланарны, при этом a , b не относятся к коллинеарным. можно вектор c разложить по двум любым векторам, только одним способом.

Определение 2

Коллинеарность векторов это — принцип соотношения параллельности векторов. Два вектора с нулевым значением, будут иметь коллинеарность, при условии, что они находятся лежат на параллельной прямой или на одной плоскости с ней.

1.5. След и определитель

Следом квадратной матрицы A (обозначается
Tr(A) или Sp(A)) называется сумма ее
диагональных элементов,

Например,

Рис. 11 След матрицы

Очевидно, что

Sp(α A) = α
Sp(A) и

Sp(A+B) =
Sp(A)+ Sp(B).

Можно показать, что

Sp(A) =
Sp(At), Sp(I) = N,

а также, что

Sp(AB) = Sp(BA).

Другой важной характеристикой квадратной матрицы является ее
определитель (обозначается det(A)). Определение
определителя в общем случае довольно сложно, поэтому мы начнем с простейшего
варианта — матрицы A размерностью (2×2)

Тогда

Для матрицы (3×3) определитель будет равен

В случае матрицы (N×N) определитель вычисляется как сумма 1·2·3· …
·N = N! слагаемых, каждый из которых равен

Индексы
k₁, k₂,…, k_N
определяются как всевозможные упорядоченные перестановки r чисел в
наборе (1, 2, … , N). Вычисление определителя матрицы — это сложная
процедура, которую на практике осуществляется с помощью специальных программ.
Например,

Рис. 12 Определитель матрицы

Отметим только очевидные свойства:

det(I) = 1,
det(A) = det(At),

det(AB) =
det(A)det(B).

Главные условия и класс компланарности векторов

Если произведение трех векторов равно нулевому значению. Данные вектора можно характеризовать как компланарные.
Когда три любых вектора независимы друг от друга, то они будут компланарными.
Когда задано несколько векторов, выполняется условие: компланарность будет характерна, для двух любых векторов, если они линейно друг от друга зависимы.

Для более лучшего восприятия материала, необходимо применить правила компланарности и коллинеарности при решении практических задач.

Для этого решим, и подробно распишем три конкретных примера.

Пример №1:

В условии задачи даны три вектора со следующими числовыми значениями.

a(1,2,3);

b(1,1,1);

c(1,2,1).

При условии, что произведение векторов будет равняться нулевому значению, можно сделать вывод о компланарности векторов.

Определяем произведение заданных значений.

Запишем все значения в виде матрицы и решим ее, применяя правила произведения и разности чисел.

a, b, с = 1*1*1+1*2*3+2*1*1-1*1*3-2*1*1-1*2*1=2 0

Так как окончательный ответ не равен нулю, а равен значению два. Следует, что вектора не являются компланарными.

Пример №2:

Заданы три вектора с положительными и отрицательными значениями. Необходимо составить и решить матрицу чисел.

a(1,-1,2);

b(0,1,-1);

c(2,-2,4).

Для решения задачи, нужно вычислить произведение значений векторов.

a, b, с=1*1*1+0*(-2)*2+(-1)*(-1)*2-2*(-1)*1-0*(-1)=0

Выполнив все действия по вычислению произведения данных, мы видим, что ответ уравнения равен нулю.

Согласно основному правило компланарности, можно сделать вывод, что вектора ему соответствую. То есть являются компланарными между собой.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Вычисление углов между двумя плоскостями

Алгоритм решения будет таков:

По трем точкам ищем уравнение первой плоскости: $ {{A}_{1}}x+{{B}_{1}}y+{{C}_{1}}z+{{D}_{1}}=0$
По другим трем точкам ищем уравнение второй плоскости: $ {{A}_{2}}x+{{B}_{2}}y+{{C}_{2}}z+{{D}_{2}}=0$
Применяем формулу: $ cos\varphi =\frac{\left| {{A}_{1}}{{A}_{2}}+{{B}_{1}}{{B}_{2}}+{{C}_{1}}{{C}_{2}}~ \right|}{\sqrt{A_{1}^{2}+B_{1}^{2}+C_{1}^{2}}\cdot \sqrt{A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}}$

Как видишь, формула очень похожа на две предыдущие, при помощи которых мы искали углы между прямыми и между прямой и плоскостью.

Так что запомнить эту тебе не составит особого труда. Сразу переходим к разбору задач:

Расстояние между двумя точками на координатной плоскости

Давай рассмотрим теперь следующую задачу: у нас есть две точки на координатной плоскости. Как найти расстояние между ними?

Пусть первая точка будет $ {{P}_{1}}({{x}_{1}},{{y}_{1}})$, а вторая $ {{P}_{2}}\left( {{x}_{2}},{{y}_{2}} \right)$.

Обозначим расстояние между ними через $ d$. Давай сделаем для наглядности следующий чертеж:

Что я сделал?

Я, во-первых, соединил точки $ {{P}_{1}}\left( {{x}_{1}},{{y}_{1}} \right)$ и $ {{P}_{2}}\left( {{x}_{2}},{{y}_{2}} \right)$.

А также из точки $ {{P}_{1}}$ провел линию, параллельную оси $ Ox$, а из точки $ {{P}_{2}}$ провел линию, параллельную оси $ Oy$.

Они пересеклись в точке $ R$, образовав при этом замечательную фигуру. Чем она замечательна?

Да мы с тобой почти что все знаем про прямоугольный треугольник. Ну уж теорему Пифагора – точно!

Искомый отрезок – это гипотенуза этого треугольника, а отрезки $ {{P}_{1}}R,~{{P}_{2}}R$ – катеты.

Чему равны координаты точки $ R$?

Да, их несложно найти по картинке: $ R\left( {{x}_{2}},{{y}_{1}} \right).~$

Так как отрезки $ {{P}_{1}}R,~{{P}_{2}}R$ параллельны осям $ Ox$ и $ Oy$ соответственно, то их длины легко найти: если обозначить длины отрезков $ {{P}_{1}}R,~{{P}_{2}}R$ соответственно через $ \left| {{P}_{1}}R\left| ,~ \right|{{P}_{2}}R \right|$, то$ \left| {{P}_{1}}R \right|={{x}_{2}}-{{x}_{1}}$$ \left| {{P}_{2}}R \right|={{y}_{2}}-{{y}_{1}}$Теперь воспользуемся теоремой Пифагора. Длины катетов нам известны, гипотенузу мы найдем:

Легко заметить, что расстояние между точками не зависит от направления.

Тогда:

Отсюда делаем три вывода:

Длина вектора = корень из суммы квадратов его координат;
Найти расстояние между двумя точками = найти длину вектора, их соединяющего (в любом направлении);
Длины векторов, соединяющих две точки в разном направлении, равны.