Как построить график корреляции excel

ПОСТРОИМ МАТРИЦУ КОЭФФИЦИЕНТОВ ПАРНОЙ КОРРЕЛЯЦИИ

1. ПОСТРОИМ МАТРИЦУ КОЭФФИЦИЕНТОВ ПАРНОЙ КОРРЕЛЯЦИИ.

Для этого рассчитаем коэффициенты парной корреляции по формуле:

Необходимые расчеты представлены в таблице 9.

—

связь между выручкой предприятия Y и объемом капиталовложений Х₁ слабая и прямая;

—

связи между выручкой предприятия Y и основными производственными фондами Х₂ практически нет;

—

связь между объемом капиталовложений Х₁ и основными производственными фондами Х₂ тесная и прямая;

Вспомогательная таблица для расчета коэффициентов парных корреляций

Также матрицу коэффициентов парных корреляций можно найти в среде Excel с помощью надстройки АНАЛИЗ ДАННЫХ, инструмента КОРРЕЛЯЦИЯ.

Матрица коэффициентов парной корреляции имеет вид:

Матрица парных коэффициентов корреляции показывает, что результативный признак у (выручка) имеет слабую связь с объемом капиталовложений х₁, а с Размером ОПФ связи практически нет. Связь между факторами в модели оценивается как тесная, что говорит о их линейной зависимости, мультиколлинеарности.

2. ПОСТРОИТЬ ЛИНЕЙНУЮ МОДЕЛЬ МНОЖЕСТВЕННОЙ РЕГРЕССИИ

Параметры модели найдем с помощью МНК. Для этого составим систему нормальных уравнений.

Расчеты представлены в таблице 10.

Решим систему уравнений, используя метод Крамера:

Вспомогательные вычисления для нахождения параметров линейной модели множественной регрессии

Линейная модель множественной регрессии имеет вид:

Если объем капиталовложений увеличить на 1 млн. руб., то выручка предприятия увеличиться в среднем на 2,317 млн. руб. при неизменных размерах основных производственных фондов.

Если основные производственные фонды увеличить на 1 млн. руб., то выручка предприятия уменьшиться в среднем на 1,171 млн. руб. при неизменном объеме капиталовложений.

коэффициент множественной корреляции:

Связь выручки предприятия с объемом капиталовложений и основными производственными фондами тесная.

67,82% изменения выручки предприятия обусловлено изменением объема капиталовложений и основных производственных фондов, на 32,18% — влиянием факторов, не включенных в модель.

F – критерий Фишера

Проверим значимость уравнения

Табличное значение F – критерия при уровне значимости α = 0,05 и числе степеней свободы d.f.₁ = k = 2 (количество факторов), числе степеней свободы d.f.₂ = (n – k – 1) = (10 – 2 – 1) = 7 составит 4,74.

Так как F_расч. = 7,375 > F_табл. = 4.74, то уравнение регрессии в целом можно считать статистически значимым.

Рассчитанные показатели можно найти в среде Excel с помощью надстройки АНАЛИЗА ДАННЫХ, инструмента РЕГРЕССИЯ.

Вспомогательные вычисления для нахождения средней относительной ошибки аппроксимации

среднюю относительную ошибку аппроксимации

В среднем расчетные значения отличаются от фактических на 3,53 %. Ошибка небольшая, модель можно считать точной.

4. Построить степенную модель множественной регрессии

Для построения данной модели прологарифмируем обе части равенства

Сделаем замену Y = lg y, A = lg a, X₁ = lg x₁, X₂ = lg x₂.

Тогда Y = A + β₁ ∙ X₁ + β₂ ∙ X₂ – линейная двухфакторная модель регрессии. Можно применить МНК.

Расчеты представлены в таблице 12.

Вспомогательные вычисления для нахождения параметров степенной модели множественной регрессии

Решаем систему уравнений применяя метод Крамера.

Степенная модель множественной регрессии имеет вид:

В степенной функции коэффициенты при факторах являются коэффициентами эластичности. Коэффициент эластичности показывает на сколько процентов измениться в среднем значение результативного признака у, если один из факторов увеличить на 1 % при неизменном значении других факторов.

Если объем капиталовложений увеличить на 1%, то выручка предприятия увеличиться в среднем на 0,897% при неизменных размерах основных производственных фондов.

Если основные производственные фонды увеличить на 1%, то выручка предприятия уменьшиться на 0,226% при неизменных капиталовложениях.

коэффициент множественной корреляции:

Связь выручки предприятия с объемом капиталовложений и основными производственными фондами тесная.

Вспомогательные вычисления для нахождения коэффициента множественной корреляции, коэффициента детерминации, ср.относ.ошибки аппроксимации степенной модели множественной регрессии

Трехмерное представление диаграммы разброса (рассеивания)

Помимо традиционного 2D-представления диаграммы разброса в настоящее время используется 3D-отображение графического представления корреляционного анализа.

Также используется матрица диаграммы рассеивания, которая отображает все парные графики на одном рисунке в матричном формате. Для n переменных матрица содержит n строк и n столбцов. Диаграмма, расположенная на пересечении i-ой строки и j-ого столбца, представляет собой график переменных Xi по сравнению с Xj. Таким образом, каждая строка и столбец являются одним измерением, отдельная ячейка отображает диаграмму рассеивания двух измерений.

Что представляет собой корреляционный анализ

Простыми словами, корреляция – это связь между двумя явлениями. В свою очередь, под корреляционным анализом подразумевают выявление этой связи. Очень частое утверждение гласит, что корреляция – это зависимость между разными объектами, но на деле это неточное определение. Ведь существует множество изображений, которые показывают связь между явлениями, которые никак не могут быть зависимы друг от друга или одного третьего фактора, который влияет на них.

Величина, определяющая степень выраженности взаимосвязи, называется коэффициентом корреляции. Это единственная величина, которая рассчитывается корреляционным анализом по сравнению с регрессионным. Возможные вариации коэффициента корреляции могут быть в пределах от -1 до 1. Если это число положительное, взаимосвязь между динамикой изменения значений прямая. Если же отрицательное, то увеличение числа 1 приводит к аналогичному уменьшению числа 2. Если число меньше единицы по модулю, то корреляция неполная. Например, увеличение числа 1 на единицу приводит к увеличению числа 2 на 0,5. В таком случае коэффициент корреляции составляет 0,5. Если же коэффициент корреляции составляет 0, то взаимосвязи между двумя переменными нет.

Интересный факт: корреляции делятся на истинные и ложные. То есть, иногда то, что графики идут в одинаковом направлении, может быть чистой случайностью, а не закономерным следствием воздействия одной переменной на другую или влияния общего фактора на обе переменные. В узких кругах довольно популярны картинки, где коррелируют между собой абсолютно не связанные явления. Вот некоторые примеры:

1. Количество человек, которые стали утопленниками в бассейнах, четко коррелирует с количеством фильмов, в которых Николас Кейдж был актером.
2. Количество съеденной моцареллы и количество человек, которые получили докторскую степень, также коррелирует на протяжении 2000-2009 годов. Наверно, действительно, моцарелла как-то влияет на мозг и стимулирует желание совершать научные открытия.
3. Почти во всех случаях средний возраст женщин, которые получили статус «Мисс Америка» коррелирует с количеством людей, которые погибли от нахождения в горячем паре.
4. Число людей, которое погибло в результате дорожно-транспортного происшествия, четко коррелирует с количеством сметаны, которое съедают люди.
5. Мало кто знает, что чем больше курятины человек ест, тем больше сырой нефти импортируется в мире. Правда, это тоже пример ложной корреляции. Кстати, импорт сырой нефти родом из Норвегии тесно связано с количеством людей, которые погибли в результате столкновения автомобиля с поездом. Причем в этом случае корреляция почти 100 процентов.
6. А еще маргарин негативно влияет на статистику разводов. Чем больше людей, которые проживали в штате Мэн, потребляли маргарина, тем выше была частота разводов. Правда, здесь еще может быть рациональное зерно. Ведь частота потребления маргарина имеет обратную корреляцию с экономическим положением в семье. В свою очередь, плохое экономическое положение в семье имеет непосредственную связь с количеством разводов. И это уже доказано научно. Так что кто знает, может, эта корреляция и не является такой ложной. Правда, никто этого не перепроверял.
7. Количество денег, которое правительство США тратит на развитие науки, космоса и технологий, имеет тесную связь с количеством самоубийств, проведенных в форме повешения или удушения.

Поэтому несмотря на то, что корреляция является эффективным статистическим инструментом, нужно учиться отфильтровывать истинные взаимосвязи между явлениями и ложные. Иначе исследование может получить такие интересные результаты. А теперь переходим непосредственно к тому, как проводить корреляционный анализ в Excel.

Вычисление коэффициента корреляции осуществляется двумя способами. Первый – это использование Мастера функций, который позволяет ввести формулу КОРРЕЛ. Второй инструмент – это пакет анализа, требующий отдельной активации.

Линейный коэффициент корреляции Пирсона

Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.

Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.

Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.

Далее будет рассматриваться только линейная корреляция. На диаграмме рассеяния (график корреляции) изображена взаимосвязь двух переменных X и Y. Пунктиром показаны средние.

При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего. Это прямая или положительная корреляция. Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.

Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.

Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?

Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.

Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.

Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число). Большая положительная ковариация говорит о прямой взаимосвязи между переменными. Обратная взаимосвязь дает отрицательную ковариацию. Если количество совпадающих по знаку отклонений примерно равно количеству не совпадающих, то ковариация стремится к нулю, что говорит об отсутствии линейной взаимосвязи.

Таким образом, чем больше по модулю ковариация, тем теснее линейная взаимосвязь. Однако значение ковариации зависит от масштаба данных, поэтому невозможно сравнивать корреляцию для разных переменных. Можно определить только направление по знаку. Для получения стандартизованной величины тесноты взаимосвязи нужно избавиться от единиц измерения путем деления ковариации на произведение стандартных отклонений обеих переменных. В итоге получится формула коэффициента корреляции Пирсона.

Показатель имеет полное название линейный коэффициент корреляции Пирсона или просто коэффициент корреляции.

Коэффициент корреляции показывает тесноту линейной взаимосвязи и изменяется в диапазоне от -1 до 1. -1 (минус один) означает полную (функциональную) линейную обратную взаимосвязь. 1 (один) – полную (функциональную) линейную положительную взаимосвязь. 0 – отсутствие линейной корреляции (но не обязательно взаимосвязи). На практике всегда получаются промежуточные значения. Для наглядности ниже представлены несколько примеров с разными значениями коэффициента корреляции.

Таким образом, ковариация и корреляция отражают тесноту линейной взаимосвязи. Последняя используется намного чаще, т.к. является относительным показателем и не имеет единиц измерения.

Диаграммы рассеяния дают наглядное представление, что измеряет коэффициент корреляции. Однако нужна более формальная интерпретация. Эту роль выполняет квадрат коэффициента корреляции r 2 , который называется коэффициентом детерминации, и обычно применяется при оценке качества регрессионных моделей. Снова представьте линию, вокруг которой расположены точки.

Линейная функция является моделью взаимосвязи между X иY и показывает ожидаемое значение Y при заданном X. Коэффициент детерминации – это соотношение дисперсии ожидаемых Y (точек на прямой линии) к общей дисперсии Y, или доля объясненной вариации Y. При r = 0,1 r 2 = 0,01 или 1%, при r = 0,5 r 2 = 0,25 или 25%.

Как рассчитать коэффициент корреляции

Давайте продемонстрируем механизм получения коэффициента корреляции на реальном кейсе. Допустим, у нас есть таблица с информацией о суммах продаж и рекламу. Нам нужно понять, в какой степени количество продаж и количество денег, которые были использованы на продвижение, взаимосвязаны.

Способ 1. Определение корреляции с помощью Мастера Функций

Функция КОРРЕЛ – один из самых простых методов, как можно реализовать поставленную задачу. В своем общем виде этот оператор имеет следующий вид: КОРРЕЛ(массив1;массив2). Как же ее ввести? Для этого нужно осуществлять следующие действия:

1. С помощью левой кнопки мыши выделяем ту ячейку, в которой будет находиться получившийся коэффициент корреляции. После этого находим слева от строки формул кнопку fx, которая откроет инструмент ввода функций. 
2. Далее выбираем категорию «Полный алфавитный перечень», в котором ищем функцию КОРРЕЛ. Как видно из названия категории, все названия функций располагаются в алфавитном порядке. 
3. Далее открывается окно ввода параметров функции. У нас два основных аргумента, каждый из которых являет собой массив данных, которые сравниваются между собой. В поле «Массив 1» указываем координаты первого диапазона, а в поле «Массив 2» – адрес второго диапазона. Для ввода данных массива, используемого для расчета, достаточно выделить нажать левой кнопкой мыши по соответствующему полю и выделить правильный диапазон. 
4. После того, как мы введем данные в аргументы, нажимаем кнопку «ОК», чем подтверждаем совершенные действия.

После выполнения описанных выше шагов мы видим в ячейке, выбранной нами на первом этапе, коэффициент корреляции. В нашем примере он составляет 0,97, что указывает на очень сильно выраженную взаимосвязь между данными двух диапазонов. 

Способ 2. Вычисление корреляции с помощью пакета анализа

Также довольно неплохой инструмент для определения корреляции между двумя диапазонами – пакет анализа. Но перед тем, как его использовать, нам надо его включить. Для этого выполняем следующие действия:

1. Нажимаем на кнопку «Файл», которая находится в левом верхнем углу сразу возле вкладки «Главная». 
2. После этого открываем раздел с настройками. 
3. В меню слева переходим в предпоследний пункт, озаглавленный, как «Надстройки». Делаем левый клик по соответствующей надписи. 
4. Открывается окно управления надстройками. Нам нужно переключить поле ввода, находящееся внизу, на пункт «Надстройки Excel» и нажать на «Перейти». Если это поле уже находится в таком положении, то не выполняем никаких изменений. 
5. Затем включаем пакет анализа в настройках. Для этого ставим соответствующую галочку и нажимаем на кнопку «ОК». 

Все, теперь наша надстройка включена. Теперь мы во вкладке «Данные» можем увидеть кнопку «Анализ данных». Если она появилась, то мы все сделали правильно. Нажимаем на нее. 

Появляется перечень с выбором разных способов анализа информации. Нам следует выбрать пункт «Корреляция» и нажать на «ОК». 

Затем нам нужно ввести настройки. Основное отличие этого метода от предыдущего заключается в том, что нам нужно вводить полностью диапазон, а не разрывать его на две части. В нашем случае, это информация, указанная в двух столбцах «Затраты на рекламу» и «Величина продаж».

Не вносим никаких изменений в параметр «Группирование». По умолчанию выставлен пункт «По столбцам», и он правильный. Эта настройка определяет, каким образом программа будет разбивать данные. Если же наши данные были бы представлены в двух рядах, то надо было бы изменить этот пункт на «По строкам».

В настройках вывода уже стоит пункт «Новый рабочий лист». То есть, информация о корреляции будет располагаться на отдельном листе. Пользователь может настроить место самостоятельно с помощью соответствующего переключателя – на текущий лист или в отдельный файл. Проверяем, все ли настройки были введены правильно. Если да, подтверждаем свои действия нажатием на клавишу «ОК».

Поскольку мы оставили поле с данными о том, куда будут выводиться результаты, таким, каким оно было, мы переходим на новый лист. На нем можно найти коэффициент корреляции. Конечно, он такой же самый, как был в предыдущем методе – 0,97. Причина этого в том, что вычисления производятся одинаковые, исходные данные мы также не меняли. Просто разными методами, но не более. 

Таким образом, Эксель дает сразу два метода осуществления корреляционного анализа. Как вы уже понимаете, в результате вычислений итог получится таким же. Но каждый пользователь может выбрать тот метод расчета, который ему больше всего подходит.

Корреляционный анализ в Excel

С помощью корреляционного анализа данных в Excel можно быстро выявить зависимость одного показателя от другого. Для упрощения реализации анализа в программу внесен специальный инструмент, который настраивается отдельно и интегрируется в документ.

1. Как проводится корреляционный анализ в Excel
2. Вариант 1: Вызов через Мастер функций
3. Вариант 2: Применение пакета анализа

Как проводится корреляционный анализ в Excel

Суть данного анализа сводится к выявлению зависимостей между различными факторами, представленными в таблицах. Таким образом можно определить как повлияет уменьшение или увеличение определенных показателей на исследуемые данные.

Если была выявлена зависимость, то определяется уже коэффициент корреляции. Коэффициент будет варьироваться в значениях от -1 до +1. При положительной корреляции, увеличение одного показателя повлечет за собой увеличение другого. Соответственно при отрицательной будет уменьшение. Чем больше значение корреляции, тем сильнее оказываемое влияние.

Для примера возьмем таблицу, где представлена прямая зависимость одних показателей от других. Например, зарплата сотрудников и величина прибыли компании. Далее рассмотрим два способа реализации корреляционного анализа на примере этой таблицы.

Вариант 1: Вызов через Мастер функций

В отличии от некоторых других типов анализов, корреляционный анализ можно вызвать с помощью функций. За него отвечает функция КОРРЕЛ вида: КОРРЕЛ(массив1;массив2):

1. Выделите ячейку в таблицу, куда хотите вставить полученный результат. В строке ввода формул воспользуйтесь значком функции.

Откроется окно мастера функций. В поле “Категория” нужно поставить значение “Полный алфавитный перечень”, чтобы отобразились все доступные для применения функции. Там отыщите пункт “КОРРЕЛ” нажмите по нему и затем на кнопку “Ок”.

Вам потребуется заполните в окошке настройки функции два поля, то есть указать два массива ячеек. В первый массив укажите номера ячеек, зависимость которых следует определить. Для рассматриваемой таблицы это будет массив столбца дохода компании. Номера можно вписать вручную или выделить их, кликнув по иконке таблицы в поле.
Во втором же массиве потребуется указать перечень ячеек, которые предположительно должны оказывать влияние на первый массив. В рассматриваемой таблице это величина зарплат сотрудников.

Закончив с заполнением нажмите кнопку “Ок”. Подсчет будет произведен автоматически и выведен в указанной ранее ячейке.
Если полученный коэффициент оказался больше +/-0.5, то это значит, что одна величина сильно зависима от другой.

Вариант 2: Применение пакета анализа

Вы можете использовать уже заданный шаблон корреляционного анализа, используя один из представленных пакетов анализа. По умолчанию пакеты анализа в Excel отключены, поэтому вам потребуется их включать отдельно.

1. Перейдите во вкладку “Файл”, что расположена в верхней части окна.

В левой части переключитесь в раздел “Параметры”.
Откройте подраздел “Надстройки”, что находятся в левой части окна с параметрами.
У строки “Управление”, что расположена в нижней части открывшегося окна, установите значение “Надстройки Excel”. Нажмите “Перейти”, чтобы увидеть перечень доступных надстроек.

В открывшемся окне установите галочку у пункта “Пакет анализа” и нажмите “Ок”. После этого у вас должны появится дополнительные инструменты в верхней панели Excel.
Нужные нам инструменты расположена во вклакде “Данные”. Там должен будет появится дополнительный блок инструментов — “Анализ”. Воспользуйтесь в нем единственным инструментом — “Анализом данных”.

Открывается список с различными вариантами анализа данных. Укажите пункт “Корреляция”. Нажмите “Ок” для применения.
В открывшемся окошке настройки анализа уже потребуется заполнить только поле “Входной интервал”. Туда добавляется сразу два массива. В нашем случае это столбцы с зарплатой и доходом фирмы.
В блоке ниже можно указать, куда будет выводится результат. По умолчанию он выводит на новый рабочий лист, но вы можете настроить вывод в новую книгу или в определенных ячейках на текущем листе. Нажмите для применения и расчетов.
В итоге вы получите тот же результат, что и в первом способе. Единственное, в некоторых таблицах, при обработке большего количества данных значений может быть гораздо больше (в основном носят вспомогательный характер).

Первый рассмотренный нами способ подойдет для большинства таблиц, в то время как второй больше подходит для таблиц с большим перечнем данных, где еще желательно отследить логику проводимого анализа.

Как рассчитать коэффициент корреляции в Excel

В сегодняшней статье речь пойдет о том, как переменные могут быть связаны друг с другом. С помощью корреляции мы сможем определить, существует ли связь между первой и второй переменной. Надеюсь, это занятие покажется вам не менее увлекательным, чем предыдущие!

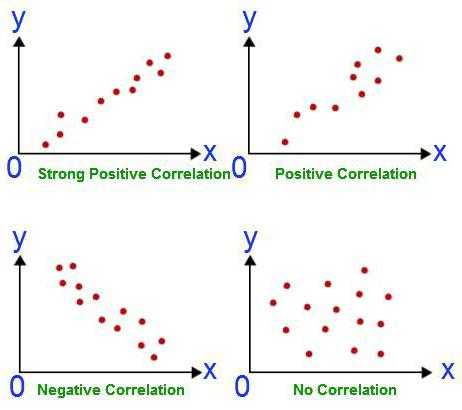
Корреляция измеряет мощность и направление связи между x и y. На рисунке представлены различные типы корреляции в виде графиков рассеяния упорядоченных пар (x, y). По традиции переменная х размещается на горизонтальной оси, а y — на вертикальной.

График А являет собой пример положительной линейной корреляции: при увеличении х также увеличивается у, причем линейно. График В показывает нам пример отрицательной линейной корреляции, на котором при увеличении х у линейно уменьшается. На графике С мы видим отсутствие корреляции между х и у. Эти переменные никоим образом не влияют друг на друга.

Наконец, график D — это пример нелинейных отношений между переменными. По мере увеличения х у сначала уменьшается, потом меняет направление и увеличивается.

Оставшаяся часть статьи посвящена линейным взаимосвязям между зависимой и независимой переменными.

Коэффициент корреляции

Коэффициент корреляции, r, предоставляет нам как силу, так и направление связи между независимой и зависимой переменными. Значения r находятся в диапазоне между — 1.0 и + 1.0. Когда r имеет положительное значение, связь между х и у является положительной (график A на рисунке), а когда значение r отрицательно, связь также отрицательна (график В). Коэффициент корреляции, близкий к нулевому значению, свидетельствует о том, что между х и у связи не существует график С).

Сила связи между х и у определяется близостью коэффициента корреляции к — 1.0 или +- 1.0. Изучите следующий рисунок.

График A показывает идеальную положительную корреляцию между х и у при r = + 1.0. График В — идеальная отрицательная корреляция между х и у при r = — 1.0. Графики С и D — примеры более слабых связей между зависимой и независимой переменными.

Коэффициент корреляции, r, определяет, как силу, так и направление связи между зависимой и независимой переменными. Значения r находятся в диапазоне от — 1.0 (сильная отрицательная связь) до + 1.0 (сильная положительная связь). При r= 0 между переменными х и у нет никакой связи.

Мы можем вычислить фактический коэффициент корреляции с помощью следующего уравнения:

Ну и ну! Я знаю, что выглядит это уравнение как страшное нагромождение непонятных символов, но прежде чем ударяться в панику, давайте применим к нему пример с экзаменационной оценкой. Допустим, я хочу определить, существует ли связь между количеством часов, посвященных студентом изучению статистики, и финальной экзаменационной оценкой. Таблица, представленная ниже, поможет нам разбить это уравнение на несколько несложных вычислений и сделать их более управляемыми.

Как видите, между числом часов, посвященных изучению предмета, и экзаменационной оценкой существует весьма сильная положительная корреляция. Преподаватели будут весьма рады узнать об этом.

Какова выгода устанавливать связь между подобными переменными? Отличный вопрос. Если обнаруживается, что связь существует, мы можем предугадать экзаменационные результаты на основе определенного количества часов, посвященных изучению предмета. Проще говоря, чем сильнее связь, тем точнее будет наше предсказание.

Использование Excel для вычисления коэффициентов корреляции

Я уверен, что, взглянув на эти ужасные вычисления коэффициентов корреляции, вы испытаете истинную радость, узнав, что программа Excel может выполнить за вас всю эту работу с помощью функции КОРРЕЛ со следующими характеристиками:

КОРРЕЛ (массив 1; массив 2),

массив 1 = диапазон данных для первой переменной,

массив 2 = диапазон данных для второй переменной.

Например, на рисунке показана функция КОРРЕЛ, используемая при вычислении коэффициента корреляции для примера с экзаменационной оценкой.

Зависимость и причинно-следственная связь

Предположим, мы вычислили коэффициент корреляции объема экспорта и ВВП. Он оказался равным единице по модулю. Провели ли мы корреляционно-регрессионный анализ до конца? Конечно же нет. Полученный результат вовсе не означает, что ВВП можно выразить через экспорт. Мы еще не доказали причинно-следственную связь между показателями. Корреляционно-регрессионный анализ – прогнозирование значений одной переменной на основе другой. Однако нужно понимать, что зачастую на параметр влияет множество факторов. Экспорт обуславливает ВВП, но не только он. Есть и другие факторы. Здесь имеет место быть и корреляция, и причинно-следственная связь, хотя и с поправкой на другие составляющие валового внутреннего продукта.

Гораздо опаснее другая ситуация. В Великобритании был проведен опрос, который показал, что дети, родители которых курили, чаще являются правонарушителями. Такой вывод сделан на основе сильной корреляции между показателя. Однако правилен ли он? Во-первых, зависимость могла быть обратной. Родители могли начать курить из-за стресса от того, что их дети постоянно попадают в переделки и нарушают закон. Во-вторых, оба параметра могут быть обусловлены третьим. Такие семьи принадлежат к низким социальным классам, для которых характерны обе проблемы. Поэтому на основе корреляции нельзя сделать вывод о наличии причинно-следственной связи.