Метод гаусса и слау

Метод Гаусса — что это такое

Метод Гаусса представляет собой методику эквивалентного преобразования исходной системы линейных уравнений в систему, решаемую существенно проще, чем исходный вариант.

Метод Гаусса используют для решения систем линейных алгебраических формул. Такой способ обладает рядом важных преимуществ:

1. Нет необходимости сравнивать уравнения для оценки совместимости.
2. Решение систем равенств, в которых число определителей совпадает или не совпадает с количеством неизвестных переменных.
3. Поиск решений для уравнений с нулевым определителем.
4. Сравнительно небольшое количество вычислительных операций для получения результата.

Матрицы: определение и свойства

Такие системы являются наиболее удобным способом представления данных, с которыми впоследствии производят манипуляции. Матрица имеет вид прямоугольника для удобства расчетов. При использовании метода Гаусса работа осуществляется с треугольными матрицами, при записи которых применяется прямоугольник с нулями на тех местах, где числа отсутствуют. Часто нули не записывают, а только подразумевают.

Важным параметром матрицы является размер:

• ширина — это количество строк, обозначают буквой m;
• длину выражают числом столбцов, записывают буквой n.

Размер матрицы будет записан в формате А m*n. В случае, когда m=n, матрица является квадратной, а m=n служит ее порядком. Номера строк и столбцов изменяются.

Определитель

Матрица обладает крайне важной характеристикой. Таким параметром является определитель

Данную величину рассчитывают с помощью диагонали. Для этого в матрице необходимо провести воображаемые диагональные линии. Затем следует найти произведение элементов, которые располагаются на этих диагоналях, а полученные значения суммировать таким образом:

1. Если диагональ обладает наклоном в правую сторону, то знак «+».
2. Для диагоналей, наклоненных влево, знак «–».

Рассчитать определитель представляется возможным лишь в случае работы с квадратной матрицей.

Если необходимо определить данный параметр для прямоугольной матрицы, то следует выполнить следующие манипуляции:

• из числа строк и числа столбцов выбрать наименьшее и обозначить его k;
• отметить в матрице произвольным образом k столбцов и k строк.

Элементы, которые расположены на пересечении отмеченных столбцов и строк, образуют новую квадратную матрицу. В случае, когда определитель является числом, не равным нулю, то данный параметр будет обозначен как базисный минор первоначальной прямоугольной матрицы. Перед решением систем уравнений методом Гаусса полезно рассчитать определитель. Если данная характеристика равна нулю, то матрица имеет бесконечное множество решений либо не имеет их вовсе. В таком случае потребуется определить ранг матрицы.

Классификация систем

Ранг матрицы является распространенным понятием. Он обозначает максимальный порядок ее определителя, который не равен нулю. По-другому можно сказать, что ранг матрицы представляет собой порядок базисного минора. Исходя из данного критерия, СЛАУ классифицируют на несколько типов. В совместных системах, которые состоят лишь из коэффициентов, ранг основной матрицы совпадает с рангом расширенной. Для подобных систем характерно одно или множество решений. По этой причине совместные системы подразделяют на следующие типы:

• определенные, обладающие одним решением, в которых наблюдается равенство ранга матрицы и количество неизвестных;
• неопределенные;
• обладающие бесконечным числом решений с рангом матрицы, который меньше количества неизвестных.

В несовместных системах ранги, характеризующие основную и расширенную матрицы, отличаются. С помощью метода Гаусса в процессе решения можно прийти либо к однозначному доказательству несовместности системы, либо к решению общего вида для системы, обладающей бесконечным количеством решений.

Последовательное исключение

Исключения Гаусса основаны на идее последовательного исключения переменных по одной до тех пор, пока не останется только одно уравнение с одной переменной в левой части. Затем это уравнение решается относительно единственной переменной. Таким образом, систему уравнений приводят к треугольной (ступенчатой) форме. Для этого среди элементов первого столбца матрицы выбирают ненулевой (а чаще максимальный) элемент и перемещают его на крайнее верхнее положение перестановкой строк. Затем нормируют все уравнения, разделив его на коэффициент a_i1, где i– номер столбца.
Затем вычитают получившуюся после перестановки первую строку из остальных строк: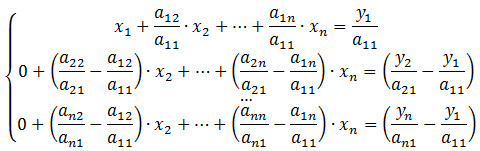
Получают новую систему уравнений, в которой заменены соответствующие коэффициенты.
После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают указанный процесс для всех последующих уравнений пока не останется уравнение с одной неизвестной: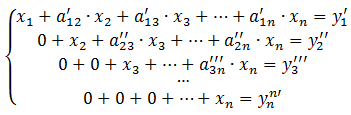

Определение СЛАУ

Определение

Системой линейных алгебраических уравнений (СЛАУ) называется система вида:

$$left{begin{array}{l} a_{11} cdot x_{1}+a_{12} cdot x_{2}+ldots+a_{1 n} cdot x_{n}=b_{1} \ a_{21} cdot x_{1}+a_{22} cdot x_{2}+ldots+a_{2 n} cdot x_{n}=b_{2} \ ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots . . \ a_{m 1} cdot x_{1}+a_{m 2} cdot x_{2}+ldots+a_{m n} cdot x_{n}=b_{m} end{array}right.$$

Упорядоченный набор значений $$left{x_{1}^{0}, x_{2}^{0}, ldots, x_{n}^{0}right}$$ называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество.

Пример

Задание. Проверить, является ли набор ${0,3}$ решением системы $left{begin{array}{l} 3 x-2 y=-6 \ 5 x+y=3 end{array}right.$

Решение. Подставляем в каждое из уравнений системы $x=0$ и $y=3$:

$$left{begin{array}{l} 3 x-2 y=-6 \ 5 x+y=3 end{array}right.$$

$$5 x+y=3 Rightarrow 5 cdot 0+3=3 Rightarrow 3=3$$

Так как в результате подстановки получили верные равенства, то делаем вывод, что заданный набор является решением указанной СЛАУ.

Ответ. Набор ${0,3}$ является решением системы $left{begin{array}{l} 3 x-2 y=-6 \ 5 x+y=3 end{array}right.$

Правила преобразования системы уравнений в матрицу

Применительно к системам уравнений в качестве чисел матрицы записывают коэффициенты и свободные члены уравнений, одно уравнение — одна строка матрицы.

Строка матрицы называется ненулевой, если хотя бы один элемент строки не равен нулю. Поэтому если в каком-либо из уравнений количество переменных разнится, то необходимо на месте отсутствующей неизвестной вписать нуль.

Столбцы матрицы должны строго соответствовать переменным. Это означает что коэффициенты переменной x могут быть записаны только в один столбец, например первый, коэффициент неизвестной y — только во второй.

При умножении матрицы все элементы матрицы последовательно умножаются на число.

Метод Гаусса

Наиболее распространенные прямые методы основаны на приведении СЛАУ к «треугольному» виду (см. матрицу Т). Это достигается последовательным исключением неизвестных из уравнений исходной системы. Сначала с помощью первого уравнения исключается X₁ из всех последующих уравнений системы, затем, используя второе уравнение, исключается X₂ из третьего и всех последующих уравнений. Этот процесс, называемый прямым ходом метода Гаусса, продолжается до тех пор, пока в левой части последнего (n-го) уравнения не останется лишь один член с неизвестным X_n, т. е. матрица системы будет приведена к треугольному виду. (Замечание: к такому виду приводится только невырожденная матрица, иначе данный метод неприменим).

Пусть методом исключения Гаусса требуется решить СЛАУ

x1+  x2+  x3–  x4= 2 ; x1–  x2–  x3+  x4= 0 ; 2x1+ x2–  x3+ 2x4= 9 ; 3x1+ x2+ 2x3–  x4= 7 .

Для удобства обозначим уравнения буквами и будем выписывать только коэффициенты при неизвестных и свободные члены уравнений. Тогда исходная СЛАУ примет вид

A₁      1  1  1 -1     2

A₂      1 -1 -1  1    0

A₃      2  1 -1  2     9

A₄      3  1  2 -1     7

Исключая члены, содержащие x₁, получим

B₁ = A₁/1              1  1  1 -1     2

B₂ = A₂ – B₁          0 -2 -2  2    -2

B₃ = A₃ – 2B₁        0 -1 -3  4    5

B₄ = A₄ – 3B₁        0 -2 -1  2    1

После исключения членов с x₂ имеем

B₁                         1  1  1 -1     2

C₂ = B₂/(-2)          0  1  1 -1     1

C₃ = B₃ + C₂        0  0 -2  3     6

C₄ = B₄ + 2C₂      0  0  1  0     3

Исключения членов с x₃ дает

В₁                         1  1  1 -1     2

С₂                        0  1  1 -1     1

D₃ = C₃ /(-2)         0  0  1 -3/2  -3

D₄ = C₄ – D₃        0  0  0  3/2  6

Продолжая аналогичные действия с последним рядом, получим

B₁                         1  1  1 -1     2

C₂                        0  1  1 -1     1

D₃                        0  0  1 -3/2  -3

E₄ = 2D₄ /3           0  0  0  1     4

Возвращаясь к общепринятой форме уравнений, запишем

x1 + x2  +  x3–  x4=  2 ; x2  +  x3–  x4=  1 ; x3–1.5 x4=  -3 ; x4=  4 .

Обратный ход метода Гаусса состоит в последовательном вычислении исходных неизвестных. Из последнего уравнения находим единственное неизвестное x₄, подставляя значение x₄в третье уравнение, x₃ – во второе и т. д., находим решение заданной СЛАУ:

x₁ = 1,   x₂ = 2,   x₃ = 3,  x₄ = 4.

Аналогично строится алгоритм для СЛАУ с произвольным числом уравнений. Необходимо помнить, что при решении СЛАУ может потребоваться операция перестановок уравнений (т. е. перестановки соответствующих коэффициентов), служащая для предотвращения деления на нулевой элемент.

Данный метод целесообразно использовать для решения систем с плотно заполненной матрицей. Все элементы матрицы и правые части системы уравнений (все вместе есть расширенная матрица) находятся в оперативной памяти ЭВМ. Объем вычислений определяется порядком системы n: число арифметических операций примерно равно (2/3)n3.

Вычисленное по методу Гаусса решение X* для СЛАУ, записанной в матричном виде A × X = B, отличается от точного решения X из-за погрешностей округления, связанных с ограниченностью разрядной сетки ЭВМ. Существуют две величины, характеризующие степень отклонения полученного решения X*от точного X. Одна из них – погрешность Е, равная разности этих значений: E = X– X*.

Решение систем линейных алгебраических уравнений

Системы линейных алгебраических уравнений (СЛАУ) появляется почти в каждой области прикладной математики. В некоторых случаях эти СЛАУ непосредственно составляют ту задачу, которую необходимо решить, в других случаях задача сводится к решению такой системы. Примерами таких задач являются системы нелинейных уравнений, дифференциальных уравнений в частных производных, задачи аппроксимации и интерполяции и др. Решение СЛАУ является одной из самых распространенных и важных задач вычислительной математики.

Систему n линейных алгебраических уравнений с n неизвестными запишем как:

a11.x1+a12.x2+…+a1n.xn=b1 ; a21.x1+a22.x2+…+a2n.xn=b2 ;  …………………………      an1.x1+an2.x2+…+ann.xn=bn .

Коэффициенты  a_i,j   (i=1, 2,…,n;   j=1,2,…,n) этой СЛАУ можно представить в виде квадратной матрицы n × n:

A =

a11a12…a1n a21a22 …a2n …………… an1an2…ann

Систему можно записать в матричном виде A×X=B, где X – вектор-столбец неизвестных; B – вектор-столбец правых частей.

Рассмотрим некоторые специальные виды матриц :

С =  1  2  3 2  7  4 3  4  8	T =  1  2  3 0  5  7 0  0  9
K =  1  2  0 0 3  4  0  0 0  0  5  6 0  0  7  8	Д =  2  3  0  0  0 1  2  3  0  0 0  3  4  5  0 0  0  4  5  6 0  0  0  1  2

Здесь С – симметричная матрица (ее элементы расположены симметрично относительно главной диагонали, т. е. a_ij=a_ji); T – верхняя треугольная матрица с равными нулю элементами, расположенными ниже диагонали; К – клеточная матрица (ее ненулевые элементы составляют отдельные группы-клетки); Д – ленточная матрица (ее ненулевые элементы составляют «ленту», параллельную диагонали; в данном случае данная матрица Д одновременно является также трехдиагональной).

Примеры решения методом Гаусса

Выше мы подробно расписали решение системы методом Гаусса. Чтобы закрепить материал, решим несколько примеров, в которых опять нам поможет метод Гаусса. Соответственно, начнём с самой простой системы.

Задача

Решить систему линейных алгебраических уравнений методом Гаусса:

Решение

Выписываем матрицу, куда добавляем столбец свободных членов:

Прежде всего мы смотрим на элемент, который находится в матрице в левом верхнем углу (первая строка, первый столбец). Для наглядности выделим цифру зелёным квадратом. На этом месте практически всегда стоит единица:

Так как

Соответственно, первая строка остаётся неизменной, а вторая поменяется:

Подбираем такое элементарное преобразование строк, чтобы во второй строке в первом столбце образовался

Как всегда у нас первая строка осталась без изменений, а вторая с новыми числами.

Итак, у нас получился ступенчатый вид матрицы:

Записываем новую систему уравнений:

Для проверки решаем систему обратным ходом. Для этого находим сначала

Так как

Подставляем в изначальную нашу систему уравнений найденные

Как видите из решения, система уравнений решена верно. Запишем ответ.

Ответ

Выше мы решали систему уравнений в двумя неизвестными, а теперь рассмотрим систему уравнений с тремя неизвестными.

Задача

Решить систему уравнений методом Гаусса:

Решение

Составляем матрицу, куда вписываем и свободные члены:

Что нам надо? Чтобы вместо цифры 2 появился 0. Для этого подбираем ближайшее число. Например, можно взять цифру -2 и на неё перемножить все элементы первой строки. Значит, умножаем

Дальше необходимо проделать те же самые действия по отношению к третьей строке. То есть, первую строку нужно умножать не на (-2), а на цифру 3, так как и в третьей строке нужно коэффициенты привести у нулю. Также первую строку умножаем на 3 и прибавляем третью строку. Получается так:

Теперь нужно обнулить элемент 7, который стоит в третьей строке во втором столбце. Для этого выбираем цифру (-7) и проделываем те же действия. Однако, необходимо задействовать вторую строку. То есть, вторую строку умножаем на (-7) и прибавляем с третьей строкой. Итак,

В результате получилась ступенчатая система уравнений:

Сначала находим

Обратный ход:

Итак, уравнение системы решено верно.

Ответ

Система с четырьмя неизвестными более сложная, так как в ней легко запутаться. Попробуем решить такую систему уравнений.

Задача

Решите систему уравнений методом Гаусса:

Решение

В уравнении

Из данного уравнения составим расширенную матрицу:

Теперь нужно умножить последние три строки (вторую, третью и четвёртую) на:

Поменяем вторую и третью строку местами и получим:

Получилось так, что

Получилась такая матрица:

Также, учитывая, что

Теперь необходимо решить уравнение обратным ходом и найдём из последнего, четвёртого уравнения

из третьего:

второе уравнение находим:

из первого уравнения:

Значит, решение системы такое: (1, 2, -1, -2).

Ответ

Добавим ещё несколько примеров для закрепления материла, но без такого подробного описания, как предыдущие системы уравнений.

Задача

Решить систему уравнений методом Гаусса:

Решение

Сначала смотрим на левое верхнее число:

Как выше уже было сказано, на этом месте должна стоять единица, но не обязательно. Производим такие действия: первую строку умножаем на -3, а потом ко второй строке прибавляем первую:

Производим следующие действия: первую строку умножаем на -1. Затем к третьей строки прибавляем вторую:

Теперь вторую строку умножаем на 1, а затем к третьей строке прибавляем вторую:

Получился ступенчатый вид уравнения:

Ответ

Система линейных алгебраических уравнений

В данной публикации мы рассмотрим определение системы линейных алгебраических уравнений (СЛАУ), как она выглядит, какие виды бывают, а также как ее представить в матричной форме, в том числе расширенной.

• Определение системы линейных уравнений
• Виды СЛАУ
• Матричная форма записи системы
• Расширенная матрица СЛАУ

Определение системы линейных уравнений

Система линейных алгебраических уравнений (или сокращенно “СЛАУ”) – это система, которая в общем виде выглядит так:

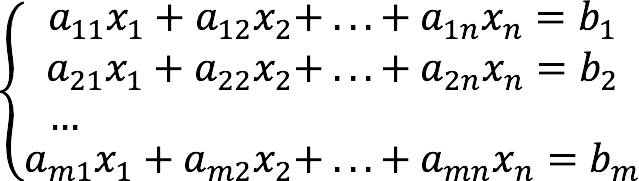
• m – количество уравнений;
• n – количество переменных.
• x₁, x₂,…, x_n – неизвестные;
• a₁₁, a₁₂,…, a_mn – коэффициенты при неизвестных;
• b₁, b₂,…, b_m – свободные члены.

Индексы коэффициентов ( a_ij ) формируются следующим образом:

• i – номер линейного уравнения;
• j – номер переменной, к которой относится коэффициент.

Решение СЛАУ – такие числа c₁, c₂,…, c_n , при постановке которых вместо x₁, x₂,…, x_n , все уравнения системы превратятся в тождества.

Виды СЛАУ

1. Однородная – все свободные члены системы равны нулю ( b₁ = b₂ = … = b_m = 0 ).
2. Неоднородная – если не выполняется условие выше.
3. Квадратная – количество уравнений равно числу неизвестных, т.е. .
4. Недоопределенная – число неизвестных больше количества уравнений.
5. Переопределенная – уравнений больше, чем переменных.

В зависимости от количества решений, СЛАУ может быть:

1. Совместная – имеет хотя бы одно решение. При этом если оно единственное, система называется определенной, если решений несколько – неопределенной.СЛАУ выше является совместной, т.к. есть хотя бы одно решение: , y = 3 .
2. Несовместная – система не имеет решений.Правые части уравнений одинаковые, а левые – нет. Таким образом, решений нет.

Матричная форма записи системы

СЛАУ можно представить в матричной форме:

• A – матрица, которая образована коэффициентами при неизвестных:
• X – столбец переменных:
• B – столбец свободных членов:

Пример Представим систему уравнений ниже в матричном виде:

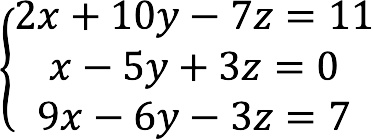
Пользуясь формами выше, составляем основную матрицу с коэффициентами, столбцы с неизвестными и свободными членами.

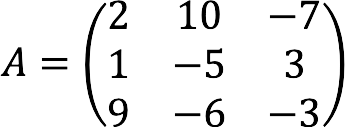
Полная запись заданной системы уравнений в матричном виде:

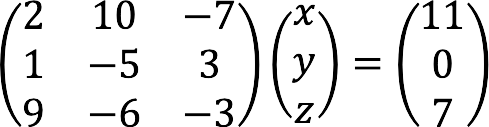
Расширенная матрица СЛАУ

Если к матрице системы A добавить справа столбец свободных членов B , разделив данные вертикальной чертой, то получится расширенная матрица СЛАУ.

Для примера выше получается так:

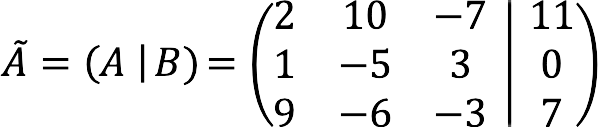
– обозначение расширенной матрицы.

Алгебраическое сложение

Способ заключается в сложении или вычитании выражений. Это довольно простой способ и в то же время эффективный. Алгоритм нахождения ответа для равенств с двумя переменными n и m сводится к следующему:

• уравниванию модулей коэффициентов при любом из неизвестных;
• сложению или вычитанию равенства;
• вычисления составленного выражения;
• прогонки каждого найденного корня через первую или вторую строчку системы уравнений;
• нахождению второго неизвестного.

То есть после выполнения арифметических действий с уравнениями должно получиться одно выражение с одним неизвестным. Затем находят значение этой переменной и в него подставляют полученный корень. Например, нужно узнать, какие корни системы, состоящей из двух строчек, превращают её в тождество:

n2 – m2 = 21.

n2 + m2 = 29.

В первую очередь необходимо сложить равенства между собой. В итоге получится:

• 2 * n 2 = 50;
• n 2 = 25;
• n = +5 (-5).

Подставив поочерёдно в каждое равенство найденные корни можно найти второе неизвестное. Для корня n = – 5 ответом будет:

• (-5)2 + m2 = 29;
• 25 + m2 = 29;
• m2 = 29 – 25;
• m2 = 4.

Существуют системы, требующие подготовительного этапа. Например, такого вида:

3 * n – 4 * m = 5.

2 * n + 3 * m = 7.

Исключить здесь сразу переменную не выйдет. Если умножить все члены первой строчки на тройку, а второй на четвёрку, получится запись:

9 * n – 12 * m = 15.

8 * n + 12 * m = 28.

Теперь равенства можно сложить, тем самым исключив переменную m. Затем система решается по базисному алгоритму. Чтобы понять, можно ли решить систему этим методом, следует предварительно её проанализировать. Необходимое условие заключается в том, что коэффициенты второй переменной должны быть одинаковыми по модулю, но противоположными по знаку.

1.2. Система двух линейных уравнений с двумя неизвестными

Покажем,
как применяются определители второго
порядка для исследования и

отыскания
решений системы двух линейных уравнений
с двумя неизвестными

(коэффициенты
,

и
свободные члены
,

считаются
при этом заданными). Напомним, что пара
чисел

Называется

решением
системы (3.3), если подстановка этих чисел
на место

и
в данную систему

обращает
оба уравнения (3.3) в тождества.

Умножая
первое уравнение системы (3.3) на —

А второе — на -и

затем
складывая полученные при этом равенства,
получим

Аналогично
путем умножения уравнений (3.3) на -исоответственно получим:

Введем
следующие обозначения:

С
помощью этих обозначений и выражения
для определителя второго порядка

уравнения
(3.4) и (3.5) могут быть переписаны в виде:

Определитель
,

составленный
из коэффициентов при неизвестных системы
(3.3), принято называть

определителем
этой системы
.
Заметим, что определители

и
получаются из

определителя
системы

посредством
замены его первого или соответственно
второго столбца свободными

Могут
представиться два случая: 1) определитель
системы

отличен
от нуля; 2) этот определитель равен нулю.

Рассмотрим
сначала случай

0.
Из уравнений (3.7) мы сразу же получаем
формулы для неизвестных,

называемые
формулами
Крамера
:

Полученные
формулы Крамера (3.8) дают решение системы
(3.7) и потому доказывают

единственность
решения исходной системы (3.3). В самом
деле, система (3.7)

является
следствием системы (3.3), поэтому всякое
решение системы (3.3) (в

случае,
если оно существует!) должно являться
решением и системы (3.7). Итак,

пока
доказано, что если у исходной системы
(3.3) существует при

0
решение, то это решение однозначно
определяется формулами Крамера (3.8).

Легко
убедиться и в существовании решения,
т. е. в том. что при

0
два числа
и

Определяемые формулами Крамера (3.8).
будучи поставлены на место неизвестных
в

уравнения
(3.3), обращают эти уравнения в тождества.
(Предоставляем читателю

самому
расписать выражения для определителей

И убедиться в справедливости указанных
тождеств.)

Мы
приходим к следующему выводу: если
определитель

системы
(3.3) отличен от нуля, то существует, и
притом единственное решение этой

системы,
определяемое формулами Крамера (3.8).

Рассмотрим
теперь случай, когда определитель

системы
равен нулю
.
Могут представиться два
подслучая
:
а) хотя

бы
один из определителей

или
,
отличен от

нуля;
б) оба определителя

и
равны нулю. (если

определитель
и

один
из двух определителей

и
равны нулю, то и

другой
из указанных двух определителей равен
нулю. В самом деле, пусть,

например
= 0

Тогда из этих пропорций получим, что

В
подслучае а) оказывается невозможным
хотя бы одно из равенств (3.7), т. е.

система
(3.7) не имеет решений, а поэтому не имеет
решений и исходная система

(3.3)
(следствием которой является система
(3.7)).

В
подслучае б) исходная система (3.3) имеет
бесчисленное множество решений. В

самом
деле, из равенств

0 и из утверждения в конце разд. 1.1
заключаем, что второе уравнение системы

(3.3)
является следствием первого и его можно
отбросить. Но одно уравнение с

двумя
неизвестными

имеет
бесконечно много решений (хотя бы один
из коэффициентов

Или
отличен от

нуля,
и стоящее при нем неизвестное может
быть определено из уравнения (3.9)

через
произвольно заданное значение другого
неизвестного).

Таким
образом, если определитель

системы
(3.3) равен нулю, то система (3.3) либо вовсе
не имеет решений (в

случае,
если хотя бы один из определителей

или
отличен от

нуля),
либо имеет бесчисленное множество
решений (в случае, когда

0). В последнем

случае
два уравнения (3.3) можно заменить одним
и при решении его одно

неизвестное
задавать произвольно.

Замечание
.
В случае, когда свободные члены

и
равны нулю,

линейная
система (3.3) называется однородной
.
Отметим, что однородная

система
всегда имеет так называемое тривиальное
решение:

0,
= 0 (эти два

числа
обращают оба однородных уравнения в
тождества).

Если
определитель однородной системы

отличен
от нуля, то эта система имеет только
тривиальное решение. Если же

=
0, то однородная система имеет бесчисленное
множество решений

(поскольку

для
однородной системы возможность отсутствия
решений исключена). Таким

образом,
однородная
система имеет нетривиальное решение в
том и только в

том
случае, когда определитель ее равен
нулю.

Метод прогонки

Он является модификацией метода Гаусса для частного случая разреженных систем – системы уравнений с трехдиагональной матрицей. Такие системы получаются при моделировании некоторых инженерных задач, а также при численном решении краевых задач для дифференциальных уравнений.

Запишем систему уравнений в виде

b₁x₁ +c₁x₂ = d₁ ;

a₂x₁ + b₂x₂  + c₂x₃  = d₂ ;

a₃x₂+ b₃x₃  + c₃x₄  = d₃ ;(8.3)

……………………………….

a_n-1x_n-2+b_n-1x_n-1+c_n-1x_n = d_n-1 ;

a_nx_n-1  +  b_nx_n = d_n. .

На главной диагонали матрицы этой системы стоят элементы b₁, b₂,…,b_n, над ней – элементы c₁, c₂,…, c_n-1, под ней – элементы a₂,a₃,a_n. При этом обычно все коэффициенты b_i не равны нулю.

Метод прогонки состоит из двух этапов – прямой прогонки (аналога прямого хода метода Гаусса) и обратной прогонки (аналога обратного хода метода Гаусса). Прямая прогонка состоит в том, что каждое неизвестное x_i выражается через x_i+1 с помощью прогоночных коэффициентов a_i, b_i:

x_i=a_i-x_i+1+b_i,    i=1, 2,…, n – 1.                            (8.4)

Из первого уравнения системы (8.3) найдем   x₁=(–c₁/b₁) x₂ + d₁/b₁.

С другой стороны, по формуле (8.4)   x₁=a₁x₂+b₁.

Приравнивая коэффициенты в обоих выражениях для x₁,получаем

a₁= – c₁/b₁,  b₁=d₁/b₁.                                            (8.5)

Из второго уравнения системы (8.3) выразим x₂ через x₃, заменяя x₁по формуле (8.4):

a₂(a₁x₂ + b₁) + b₂x₂ + c₂x₃ = d₂.

Отсюда найдем x₂ = (– c₂x₃ + d₂ – a₂b₁) / (a₂a₁ + b₂),

или              x₂=a₂x₃ + b₂ ;

a₂= – c₂/e₂ ;

b₂=(d₂ – a₂b₁)/e₂ ;

e₂=a₂a₁+b₂  .

Аналогично можно вычислить прогоночные коэффициенты для любого номера i:

a_i = – c_i/e_i ,  b_i=(d_i – a_ib_i-1)/e_i  ;(8.6)

e_i = a_ia_i-1 + b_i ,i = 2, 3,…, n – 1 .

Обратная прогонка состоит в последовательном вычислении неизвестных x_i. Сначала нужно найти x_n . Для этого воспользуемся выражением (8.4) при i = n – 1 и последним уравнением системы (8.3). Запишем их:

x_n-1= a_n-1x_n+b_n-1 ;

a_nx_n-1+b_nx_n= d_n .

Отсюда, исключая x_n-1, находим   x_n = (d_n – a_nb_n-1)/(b_n+a_na_n-1).

Матричная запись[]

СЛАУ может быть представлена и в матричной форме:

(a11a12⋯a1na21a22⋯a2n⋮⋮⋱⋮am1am2⋯amn)(x1x2⋮xn)=(b1b2⋮bm){\displaystyle {\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{pmatrix}}{\begin{pmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{pmatrix}}={\begin{pmatrix}b_{1}\\b_{2}\\\vdots \\b_{m}\end{pmatrix}}}

или:

Ax=b{\displaystyle Ax=b}.

Здесь A{\displaystyle A} — это матрица системы, x{\displaystyle x} — столбец неизвестных, а b{\displaystyle b} — столбец свободных членов. Если к матрице A{\displaystyle A} приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.
Теорема Кронекера — Капелли устанавливает необходимое и достаточное условие совместности системы линейных алгебраических уравнений посредством свойств матричных представлений: система совместна тогда и только тогда, когда ранг её матрицы совпадает с рангом расширенной матрицы.

Следствия из теоремы Кронекера — Капелли

Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).

Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).

В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.

Рекомендую подробно изучить предметы:

Математика Алгебра Линейная алгебра Векторная алгебра Высшая математика Дискретная математика Математический анализ Математическая логика

Ещё лекции с примерами решения и объяснением:

• Скалярное произведение и его свойства
• Векторное и смешанное произведения векторов
• Преобразования декартовой системы координат
• Бесконечно малые и бесконечно большие функции
• Критерий совместности Кронекера-Капелли
• Формулы Крамера
• Матричный метод
• Экстремум функции

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

1.1. Понятие матрицы и определителя второго порядка

Прямоугольную
таблицу из чисел,

матрицей.
Для обозначения матрицы используют
либо сдвоенные вертикальные

черточки,
либо круглые скобки. Например:

1
7 9.2 1 7 9.2

28
20 18 28 20 18

6
11 2 -6 11 2

Если
число строк матрицы совпадает с числом
ее столбцов, то матрица называется

квадратной.
Числа, входящие в состав матрицы, называют
ее элементами
.

Рассмотрим
квадратную матрицу, состоящую из четырех
элементов:

Определителем
второго порядка, соответствующим матрице
(3.1), называется число,

и
обозначаемое символом

Итак,
по определению

Элементы,
составляющие матрицу данного определителя,
обычно называют

элементами
этого определителя.

Справедливо
следующее утверждение: для
того чтобы определитель второго

порядка
был равен нулю, необходимо и достаточно,
чтобы элементы его строк (или

соответственно
его столбцов) были пропорциональны
.

Для
доказательства этого утверждения
достаточно заметить, что каждая из

пропорций
/

эквивалентна
равенству

А последнее равенство в силу (3.2)
эквивалентно обращению в нуль определителя.

Прямые методы

Прямые методы используют заранее известное, зависящее от n, количество соотношений (формул) для вычисления неизвестных. К ним относятся правило Крамера, метод Гаусса (или метод последовательного исключения неизвестных), метод Гаусса с выбором главного элемента, метод прогонки (частный случай метода Гаусса для СЛАУ с трехдиагональной матрицей), метод Жордана (часто используется для нахождения обратной матрицы), метод квадратного корня (применяется тогда, когда матрица системы является симметричной), клеточные методы (используются для решения больших СЛАУ, когда матрица и вектор правых частей целиком не помещаются в оперативной памяти ЭВМ) и др. Алгоритмы этих методов сравнительно просты и наиболее универсальны, т. е. пригодны для решения широкого класса СЛАУ. К недостаткам таких методов относится требование хранения в оперативной памяти ЭВМ сразу всей исходной матрицы, и, следовательно, при больших значениях n используется большой объем памяти. Прямые методы не учитывают конкретный вид матрицы или ее структуру, т. е. при большом числе нулевых элементов в ленточных или клеточных матрицах эти элементы занимают место в памяти ЭВМ, и над ними проводятся практически бесполезные арифметические операции. Кроме того, существенным недостатком прямых методов является увеличение погрешностей в процессе получения решения, т. к. вычисления на последующем этапе используют результаты предыдущих операций, полученных, в свою очередь, с какой-то погрешностью. Особенно актуальным становится вышеуказанное обстоятельство для больших СЛАУ вследствие резкого увеличения общего количества числа арифметических действий, а также для плохо обусловленных СЛАУ из-за их чувствительности к погрешностям.

Метод подстановки

Систему равенств возможно решить и способом подстановки. Используя любое из уравнений, можно выразить любую из неизвестных переменных, а затем подставить её в другое равенство. Алгоритм использования метода следующий:

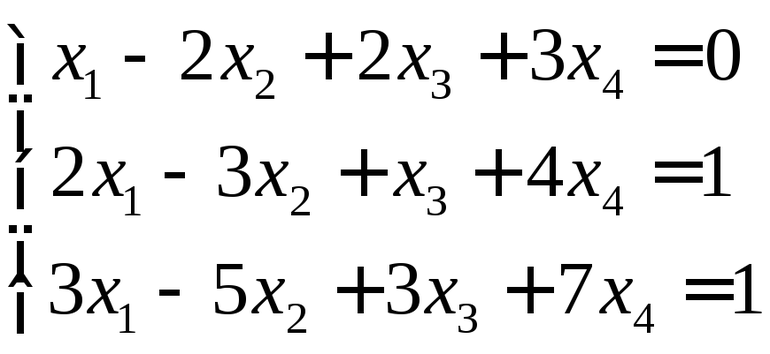
• через n в одном из уравнений выражают m;
• подставляют полученное равенство вместо n в другое тождество;
• решают уравнение и находя m;
• поочерёдно подставляют найденные корни и получают ответ.

8 * n – 5 * m = -16.

10 * n + 3 * m = 17.

Выразив m через n можно записать равенство: n = (8* m + 16) / 5. Так как n одинаково в обоих уравнениях, то следует подставить полученное тождество и записать: 10* n + 3*(8* n +16) / 5 = 17. Отсюда уже просто найти корень. Он будет равен дроби 1/2. Подставив его вместо n легко вычислить и второй корень: m = (8 * n + 16) / 5 = 4. Таким образом, у системы будет только один целый корень. При желании проверить ответ можно решить систему другим методом.