Примеры решения задач с матрицами

Отыскание ранга матрицы способом окаймляющих миноров

Окаймляющим минором называется минор большего порядка по отношению
к данному, если этот минорм большего порядка содержит в себе данный минор.

Например, дана матрица

.

Возьмём минор

,

окаймляющими будут такие миноры:

.

Алгоритм нахождения ранга матрицы следующий.

1. Находим не равные нулю миноры второго порядка. Если все миноры
второго порядка равны нулю, то ранг матрицы будет равен единице ().

2. Если существует хотя бы один минор второго порядка, не равный
нулю, то составляем окаймляющие миноры третьего порядка. Если все окаймляющие миноры
третьего порядка равны нулю, то ранг матрицы равен двум ().

3. Если хотя бы один из окаймляющих миноров третьего порядка не равен
нулю, то составляем окаймляющие его миноры. Если все окаймляющие миноры четвёртого
порядка равны нулю, то ранг матрицы равен трём ().

4. Продолжаем так, пока позволяет размер матрицы.

Пример 1. Найти ранг матрицы

.

Решение. Минор второго порядка .

Окаймляем его. Окаймляющих миноров будет четыре:

,

,

,

.

Таким образом, все окаймляющие миноры третьего порядка равны нулю,
следовательно, ранг данной матрицы равен двум ().

Проверить решение можно на калькуляторе онлайн Вычисление ранга матрицы.

Пример 2. Найти ранг матрицы

.

Решение. Ранг данной матрицы равен 1, так как все миноры второго
порядка этой матрицы равны нулю (в этом, как и в случаях окаймляющих миноров в двух следующих примерах,
дорогим студентам предлагается убедиться самостоятельно, возможно, используя
правила вычисления определителей), а среди миноров первого порядка, то есть среди
элементов матрицы, есть не равные нулю.

Проверить решение можно на калькуляторе онлайн Вычисление ранга матрицы.

Пример 3. Найти ранг матрицы

.

Решение. Минор второго порядка этой матрицы
,
в все миноры третьего порядка этой матрицы равны нулю. Следовательно, ранг данной матрицы
равен двум.

Проверить решение можно на калькуляторе онлайн Вычисление ранга матрицы.

Пример 4. Найти ранг матрицы

.

Решение. Ранг данной матрицы равен 3, так как единственный минор
третьего порядка этой матрицы равен 3.

Проверить решение можно на калькуляторе онлайн Вычисление ранга матрицы.

Общие понятия, основные формулы

Предположим, что существует какая-то квадратная матрица или квадратная матрица n-го порядка:

\(A_{n\times n}\)

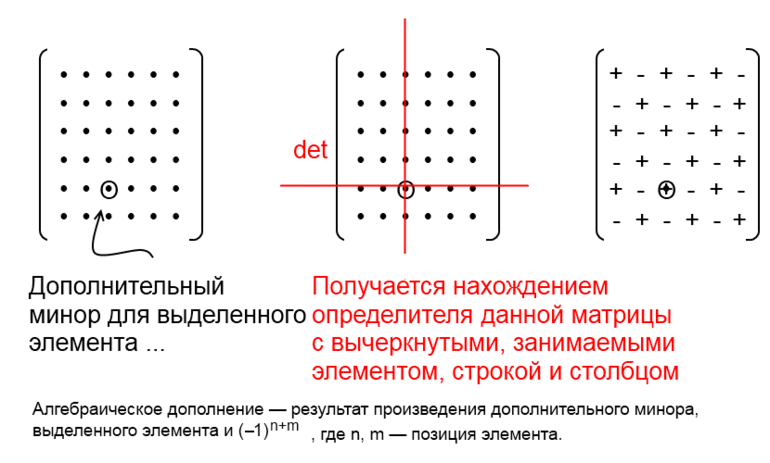
\(Минор \ M_{ij} \ элемента \ a_{ij} \ матрицы \ A_{n\times n}\) будет являться определитель матрицы, которая получается из матрицы A в результате устранения i-й строки и j-го столбца, которые расположены таким образом, что их пересечение совпадает с элементом \(a_{ij}.\)

В качестве доказательства можно рассмотреть такую квадратную матрицу четвертого порядка:

\(A=\left( \begin{array} {cccc} 1 & 0 & -3 & 9\\ 2 & -7 & 11 & 5 \\ -9 & 4 & 25 & 84\\ 3 & 12 & -5 & 58 \end{array} \right)\)

Необходимо определить минор для элемента \(a_{32}\), то есть \(M_{32}\). В первую очередь следует записать минор \(M_{32}\), а затем рассчитать его. Порядок действий для составления \(M_{32}\) включает вычерк из матрицы A третьей строки и второго столбца. Данное действие обусловлено тем, что элемент \(a_{32}\) расположен там, где третья строка и второй столбец пересекаются. Таким образом, была получена новая матрица с определителем в виде искомого минора \(M_{32}\).

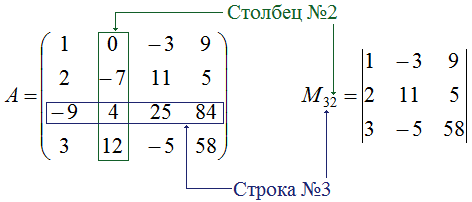
Данный минор достаточно просто рассчитать с помощью теоремы для вычисления определителей второго и третьего порядков. Расчет будет следующий:

\(M_{32}=\left| \begin{array} {ccc} 1 & -3 & 9\\ 2 & 11 & 5 \\ 3 & -5 & 58 \end{array} \right|= 1\cdot 11\cdot 58+(-3)\cdot 5\cdot 3+2\cdot (-5)\cdot 9-9\cdot 11\cdot 3-(-3)\cdot 2\cdot 58-5\cdot (-5)\cdot 1=579\)

Таким образом, минор элемента \(a_{32}\) равен 579, то есть \(M_{32}=579\)

Примечание

Нередко в тематической литературе вместо «минор элемента матрицы» употребляют понятие «минор элемента определителя». Смысл выражения сохраняется. Таким образом, для вычисления минора элемента \(a_{ij}\) требуется исключить из начального определителя i-ю строку и j-й столбец. Элементы, которые остались, следует записать в новый определитель, который представляет собой минор элемента \(a_{ij}.\)

В качестве примера можно рассчитать минор элемента \(a_{12}\) определителя:

\(\left| \begin{array} {ccc} -1 & 3 & 2\\ 9 & 0 & -5 \\ 4 & -3 & 7 \end{array} \right|\)

В первую очередь нужно записать искомый минор \(M_{12}\). Для этого можно исключить из заданного определителя первую строку и второй столбец:

Вычислить минор целесообразно с помощью формулы для расчета определителей второго и третьего порядков:

\(M_{12}=\left| \begin{array} {cc} 9 & -5\\ 4 & 7 \end{array} \right|=9\cdot 7-(-5)\cdot 4=83\)

В результате минор элемента \(a_{12}\) составит 83, то есть \(M_{12}=83\)

Предположим, что существует какая-то квадратная матрица \(A_{n\times n}\), то есть квадратная матрица n-го порядка. Алгебраическое дополнение \(A_{ij}\) элемента \(a_{ij}\) матрицы \(A_{n\times n}\) можно определить, используя формулу:

\(A_{ij}=(-1)^{i+j}\cdot M_{ij},\)

где \(M_{ij}\) является минором элемента \(a_{ij}.\)

В качестве примера можно рассчитать алгебраическое дополнение элемента \(a_{32}\) матрицы:

\(A=\left( \begin{array} {cccc} 1 & 0 & -3 & 9\\ 2 & -7 & 11 & 5 \\ -9 & 4 & 25 & 84\\ 3 & 12 & -5 & 58 \end{array} \right)\)

В результате необходимо получить значение для \(A_{32}\). В предыдущем примере уже был расчет для минора \(M_{32}=579\), поэтому целесообразно в данной задаче использовать имеющиеся данные:

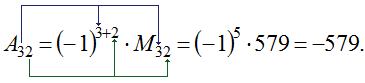
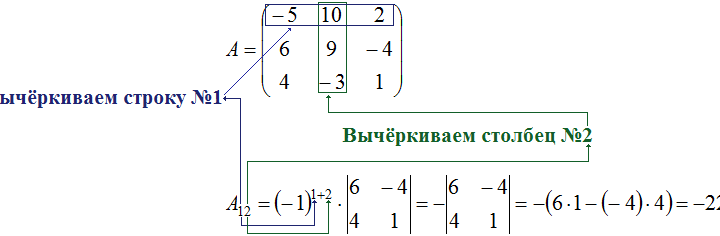
Как правило, при определении алгебраических дополнений не требуется выполнять отдельный расчет минора перед вычислением непосредственно дополнения. К примеру, если требуется определить \(A_{12}\) при условии, что:

\(A=\left( \begin{array} {ccc} -5 & 10 & 2\\ 6 & 9 & -4 \\ 4 & -3 & 1 \end{array} \right)\)

Необходимо записать справедливое равенство:

\(A_{12}=(-1)^{1+2}\cdot M_{12}=-M_{12}\)

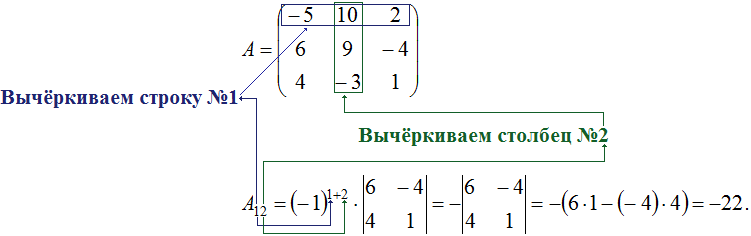
Рассчитать \(M_{12}\) легко с помощью вычерка первой строки и второго столбца матрицы А. Поэтому нет необходимости вводить лишнее обозначение для минора. Достаточно сразу записать уравнение для алгебраического дополнения \(A_{12}\):

Понятие ранга матрицы

Ранг матрицы используется при проверке условия совместности системы
линейных уравнений.

Определение. Рангом матрицы называется максимальное
число линейно независимых строк, рассматриваемых как векторы.

Можно открыть в новом окне материал о линейной независимости векторов.

Теорема 1 о ранге матрицы. Рангом матрицы называется максимальный
порядок отличного от нуля минора матрицы.

Понятие минора мы уже разбирали на ,
а сейчас обобщим его. Возьмём в матрице сколько-то строк и сколько-то
столбцов, причём это «сколько-то» должно быть меньше числа строк и стобцов матрицы,
а для строк и столбцов это «сколько-то» должно быть одним и тем же числом. Тогда на
пересечении скольки-то строк и скольки-то столбцов окажется матрица меньшего порядка,
чем наша исходная матрица. Определитель это матрицы и будет минором k-го порядка, если
упомянутое «сколько-то» (число строк и столбцов) обозначим через k.

Определение. Минор (r+1)-го порядка, внутри
которого лежит выбранный минор r-го порядка, называется называется окаймляющим для
данного минора.

Наиболее часто используются два способа отыскания ранга матрицы. Это способ
окаймляющих миноров и способ элементарных преобразований (методом Гаусса).

При способе окаймляющих миноров используется следующая теорема.

Теорема 2 о ранге матрицы. Если из элементов матрицы
можно составить минор r-го порядка, не равный нулю, то ранг матрицы равен r.

При способе элементарных преобразований используется следующее свойство:

— если путём элементарных преобразований получена трапециевидная матрица,
эквивалентная исходной, то рангом этой матрицы является число строк в ней кроме строк,
полностью состоящих из нулей.

Алгебраическое дополнение $A_{ij}$ элемента $a_{ij}$

Пусть задана квадратная матрица $A_{n\times n}$ (т.е. квадратная матрица n-го порядка).

Алгебраическое дополнением
$A_{ij}$ элемента
$a_{ij}$ матрицы $A_{n\times n}$ находится по следующей формуле:
$$
A_{ij}=(-1)^{i+j}\cdot M_{ij},
$$

где $M_{ij}$ — минор элемента $a_{ij}$.

Найдем алгебраическое дополнение элемента $a_{32}$ матрицы $A=\left(\begin{array} {ccc}
1 & 0 & -3 & 9\\
2 & -7 & 11 & 5 \\
-9 & 4 & 25 & 84\\
3 & 12 & -5 & 58 \end{array} \right)$, т.е. найдём $A_{32}$. Ранее мы уже находили минор $M_{32}=579$, поэтому используем полученный результат:

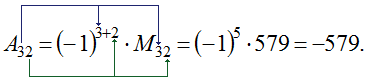
Обычно при нахождении алгебраических дополнений не вычисляют отдельно минор, а уж потом само дополнение. Запись минора опускают. Например, найдем $A_{12}$, если $A=\left(\begin{array} {ccc}
-5 & 10 & 2\\
6 & 9 & -4 \\
4 & -3 & 1 \end{array} \right)$. Согласно формуле $A_{12}=(-1)^{1+2}\cdot M_{12}=-M_{12}$. Однако чтобы получить $M_{12}$ достаточно вычеркнуть первую строку и второй столбец матрицы $A$, так зачем же вводить лишнее обозначение для минора? Сразу запишем выражение для алгебраического дополнения $A_{12}$:

Как найти определитель матрицы?

Чтобы найти определитель матрицы вводят понятие «минор». Обозначение: M_ij — минор,
M_ij2 — минор второго порядка (определитель матрицы 2*2) и т.д.

Чтобы найти минор для элемента a_ij, вычеркиваем из матрицы A i-ю строку и j-й столбец. Получаем матрицу
размерностью n-1*m-1, находим определитель этой матрицы.

Пример: найти минор второго порядка для элемента a₁₂ матрицы A:

Решение:

Вычеркиваем из матрицы A 1-ю строку и 2-й столбец. Получаем матрицу размерностью 2*2, находим определитель этой матрицы:

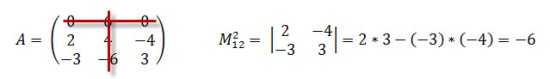
Ответ: -6.

Таким образом, минор — это не матрица, а число.

Пример: найти определитель (в общем виде) матрицы 2*2 разложением по 1) строке; 2) столбцу:

Решение:

По строке: det A = a₁₁*(-1)1+1*M₁₁+a₁₂*(-1)1+2*M₁₂ = a₁₁*1*a₂₂+a₁₂*(-1)*a₂₁ == a₁₁*a₂₂-a₁₂*a₂₁

По столбцу: det A = a₁₁*(-1)1+1*M₁₁+a₂₁*(-1)2+1*M₂₁ = a₁₁*1*a₂₂+a₂₁*(-1)*a₁₂ == a₁₁*a₂₂-a₂₁*a₁₂

Несложно увидеть, что получен одинаковый результат.

Таким образом, чтобы найти определитель матрицы 2*2 достаточно из произведения элементов
главной диагонали вычесть произведение элементов побочной:

Миноры матричного калькулятора

Поиск инструмента

Миноры матрицы

Инструмент для вычисления миноров матрицы, т.

Результаты

Миноры матрицы — dCode

Теги: Matrix

Share

dCode и другие

dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!

Запись в dCode

Загрузка… (если это сообщение не исчезнет, ​​попробуйте обновить эту страницу)

См. также: Определитель матрицы

Ответы на вопросы (FAQ)

Что такое минор матрицы? (Определение)

Миноры квадратной матрицы $M = m_{i, j}$ размера $n$ — это определители квадратных подматриц, полученные удалением строки $i$ и столбца $j$ из $M$ .

Иногда миноры определяются путем удаления противоположных строк и столбцов (т.

Как вычислить матрицу миноров?

Для квадратной матрицы второго порядка нахождение миноров — это вычисление матрицы кофакторов без коэффициентов.

Для больших матриц, таких как 3×3, вычислите определители каждой подматрицы.

Пример: $$ M = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} $$

Определитель подматрицы получается удалением первой строки и первого столбца: $ei-fh $$, проделайте то же самое для всех комбинаций строк и столбцов.

В чем разница между минором и кофактором?

Для квадратной матрицы минор идентичен кофактору, за исключением знака (действительно, кофакторы могут иметь — знак в зависимости от их положения в матрице). Несовершеннолетние не принимают этот знак минус.

Исходный код

dCode сохраняет за собой право собственности на исходный код Minors of a Matrix. За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Миноры матрицы», апплета или фрагмента (конвертер, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Миноры Матрицы» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т.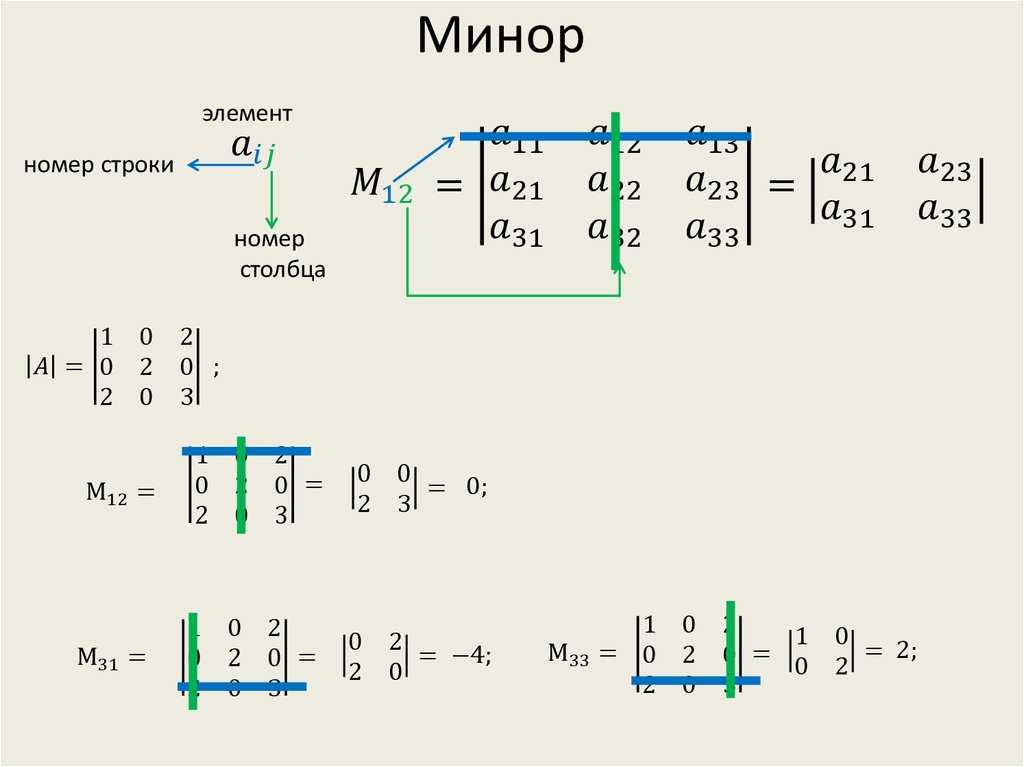

Цитировать dCode

Копирование и вставка страницы «Миноры матрицы» или любых ее результатов разрешено, если вы цитируете dCode! Цитировать как источник (библиографию): Minors of a Matrix на dCode.fr , получено 08 декабря 2022 г., https://www.dcode.fr/matrix-minors

Сводка

• Калькулятор миноров матрицы NxN
• Что такое минор матрицы? (Определение)
• Как вычислить миноры матрицы?
• В чем разница между минором и кофактором?

Similar pages

• Determinant of a Matrix
• Characteristic Polynomial of a Matrix
• Jordan Normal Form Matrix
• Matrix Subtraction
• Inverse of a Matrix
• Schur Decomposition (Matrix)
• Adjoint Matrix
• DCODE’S TOOLS СПИСОК

Поддержка

• Paypal
• Patreon
• Подробнее

Форум/Помощь

Ключевые слова

минор,матрица,детерминант,квадрат

Ссылки

4.Определители. Свойства определителей.

Квадратной матрице А порядка n можно сопоставить число det А (или |A|, или ), называемое ее определителем, следующим образом:

Определитель матрицы A также называют ее детерминантом. Правило вычисления детерминанта для матрицы порядка N является довольно сложным для восприятия и применения. Однако известны методы, позволяющие реализовать вычисление определителей высоких порядков на основе определителей низших порядков. Один из методов основан на свойстве разложения определителя по элементам некоторого ряда (свойство 7). При этом заметим, что определители невысоких порядков (1, 2, 3) желательно уметь вычислять согласно определению.

Вычисление определителя 2-го порядка иллюстрируется схемой:

Пример 4.1. Найти определители матриц

Решение:

При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса), которое символически можно записать так:

Пример 4.2. Вычислить определитель матрицы

Решение:

det А = 5*1*(-3) + (-2)*(-4)*6 + 3*0*1 — 6*1*1 — 3*(-2)*(-3) — 0*(-4)*5 = -15+48-6-18 = 48-39 = 9.

Сформулируем основные свойства определителей, присущие определителям всех порядков. Некоторые из этих свойств поясним на определителях 3-го порядка.

Свойство 1 («Равноправность строк и столбцов»). Определитель не изменится, если его строки заменить столбцами, и наоборот. Иными словами,

В дальнейшем строки и столбцы будем просто называть рядами определителя.

Свойство 2. При перестановке двух параллельных рядов определитель меняет знак.

Свойство 3. Определитель, имеющий два одинаковых ряда, равен нулю.

Свойство 4. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.

Действительно,

Свойство 5. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

Например,

Свойство 6. («Элементарные преобразования определителя»). Определитель не изменится, если к элементам одною ряда прибавить соответствующие элементы параллельного ряда, умноженные па любое число.

Пример 4.3. Доказать, что

Решение: Действительно, используя свойства 5, 4 и 3 подучим

Дальнейшие свойства определителей связаны с понятиями минора и алгебраического дополнения.

Минором некоторого элемента аij определителя n-го порядка называется определитель n — 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, па пересечении которых находится выбранный элемент. Обозначается mij

Алгебраическим дополнением элемента aij определителя называется его минор, взятый со знаком «плюс», если сумма i + j четное число, и со знаком «минус», если эта сумма нечетная. Обозначается Aij :

Свойство 7 («Разложение определителя по элементам некоторого ряда»). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.

Проиллюстрируем и одновременно докажем свойство 7 на примере определителя 3-его порядка. В этом случае свойство 7 означает, что

В самом деле, имеем

Свойство 7 содержит в себе способ вычисления определителей высоких порядков.

Пример 4.4. Вычислите определитель матрицы

Решение: Для разложения определителя обычно выбирают гот ряд, где есть нулевые элементы, т. к. соответствующие им слагаемые в разложении будут равны нулю.

Свойство 8. Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
Так, например,

Posted in Высшая математика, Лекции 1 курс and tagged Высшая математика

Судебная власть Индианы: калькулятор алиментов

Закрыть меню

• Судебная власть Индианы
• Услуги
• Текущий:
  Калькулятор алиментов

Для родителей

Расчет алиментов онлайн

Используйте этот калькулятор для расчета еженедельных выплат алиментов и подготовки форм для использования в суде.

Получить юридическую помощь

Даже если вы не нанимаете адвоката для ведения вашего дела, вы можете поговорить с адвокатом до подачи юридических документов (или бумаг) в суд. Здесь вы можете найти информацию о том, как получить юридическую помощь, в том числе о том, как найти недорогую или бесплатную юридическую помощь (бесплатно).

Расчет алиментов онлайн

Используйте этот калькулятор для расчета еженедельных выплат алиментов и подготовки форм для использования в суде. Введите информацию о детях, доходе, родительском времени, медицинском обслуживании и других расходах и создайте только те формы, которые вам нужны.

Минор k-го порядка матрицы $A_$

Если в предыдущих двух пунктах мы говорили лишь о квадратных матрицах, то здесь поведём речь также и о прямоугольных матрицах, у которых количество строк вовсе не обязательно равняется количеству столбцов. Итак, пусть задана матрица $A_$, т.е. матрица, содержащая m строк и n столбцов.

Например, рассмотрим такую матрицу:

$$A=left( egin -1 & 0 & -3 & 9\ 2 & 7 & 14 & 6 \ 15 & -27 & 18 & 31\ 0 & 1 & 19 & 8\ 0 & -12 & 20 & 14\ 5 & 3 & -21 & 9\ 23 & -10 & -5 & 58 end
ight) $$

Запишем для неё какой-либо минор третьего порядка. Чтобы записать минор третьего порядка нам потребуется выбрать какие-либо три строки и три столбца данной матрицы. Например, возьмём строки №2, №4, №6 и столбцы №1, №2, №4. На пересечении этих строк и столбцов будут располагаться элементы требуемого минора. На рисунке элементы минора показаны синим цветом:

Миноры первого порядка находятся на пересечении одной строки и одного столбца, т.е. миноры первого порядка равны элементам заданной матрицы.

Напомню, что главными диагональными элементами именуют те элементы матрицы, у которых индексы равны: $a_<11>$, $a_<22>$, $a_<33>$ и так далее. Например, для рассмотренной выше матрицы $A$ такими элементами будут $a_<11>=-1$, $a_<22>=7$, $a_<33>=18$, $a_<44>=8$. На рисунке они выделены зелёным цветом:

$$left( egin oldgreen <-1>& 0 & -3 & 9\ 2 & oldgreen <7>& 14 & 6 \ 15 & -27 & oldgreen <18>& 31\ 0 & 1 & 19 & oldgreen<8>\ 0 & -12 & 20 & 14\ 5 & 3 & -21 & 9\ 23 & -10 & -5 & 58 end
ight) $$

Например, если в матрице $A$ мы вычеркнем строки и столбцы с номерами 1 и 3, то на их пересечении будут расположены элементы минора второго порядка, на главной диагонали которого будут находиться только диагональные элементы матрицы $A$ (элементы $a_<11>=-1$ и $a_<33>=18$ матрицы $A$). Следовательно, мы получим главный минор второго порядка:

$$ M=left|egin oldgreen <-1>& -3 \ 15 & oldgreen <18>end
ight| $$

Естественно, что мы могли взять иные строки и столбцы, – например, с номерами 2 и 4, получив при этом иной главный минор второго порядка.

Для примера рассмотрим такую матрицу:

$$A=left( egin -1 & 0 & 3 & 0 & 0 \ 2 & 0 & 4 & 1 & 0\ 1 & 0 & -2 & -1 & 0\ 0 & 0 & 0 & 0 & 0 end
ight) $$

Запишем минор этой матрицы, элементы которого расположены на пересечении строк №1, №2, №3 и столбцов с №1, №3, №4. Мы получим минор третьего порядка (его элементы выделены в матрице $A$ фиолетовым цветом):

Найдём значение этого минора, используя формулу №2 из темы вычисления определителей второго и третьего порядков:

$$ M=left| egin -1 & 3 & 0\ 2 & 4 & 1 \ 1 & -2 & -1 end
ight|=4+3+6-2=11. $$

Итак, $M=11
eq 0$. Теперь попробуем составить любой минор, порядок которого выше трёх. Чтобы составить минор четвёртого порядка, нам придётся использовать четвёртую строку, однако все элементы этой строки равны нулю. Следовательно, в любом миноре четвёртого порядка будет нулевая строка, а это означает, что все миноры четвёртого порядка равны нулю. Миноры пятого и более высоких порядков составить мы не можем, так как матрица $A$ имеет всего 4 строки.

Мы нашли минор третьего порядка, не равный нулю. При этом все миноры высших порядков равны нулю, следовательно, рассмотренный нами минор – базисный. Строки матрицы $A$, на которых расположены элементы этого минора (первая, вторая и третья), – базисные строки, а первый, третий и четвёртый столбцы матрицы $A$ – базисные столбцы.

Данный пример, конечно, тривиальный, так как его цель – наглядно показать суть базисного минора. Вообще, базисных миноров может быть несколько, и обычно процесс поиска такого минора куда сложнее и объёмнее.

Введём ещё одно понятие – окаймляющий минор.

Для примера обратимся к такой матрице:

$$A=left( egin -1 & 2 & 0 & -2 & -14\ 3 & -17 & -3 & 19 & 29\ 5 & -6 & 8 & -9 & 41\ -5 & 11 & 19 & -20 & -98\ 6 & 12 & 20 & 21 & 54\ -7 & 10 & 14 & -36 & 79 end
ight) $$

Запишем минор второго порядка, элементы которого расположены на пересечении строк №2 и №5, а также столбцов №2 и №4. Эти элементы выделены в матрице красным цветом:

Добавим к набору строк, на которых лежат элементы минора $M$, ещё строку №1, а к набору столбцов – столбец №5. Получим новый минор $M’$ (уже третьего порядка), элементы которого расположены на пересечении строк №1, №2, №5 и столбцов №2, №4, №5. Элементы минора $M$ на рисунке выделены красным цветом, а элементы, которые мы добавляем к минору $M$ – синим:

Минор $M’$ является окаймляющим минором для минора $M$. Аналогично, добавляя к набору строк, на которых лежат элементы минора $M$, строку №4, а к набору столбцов – столбец №3, получим минор $M»$ (минор третьего порядка):

Минор $M»$ также является окаймляющим минором для минора $M$.

Приведение матрицы к треугольному виду, преобразование матрицы, облегчающее вычисление определителя

Показанные ниже методы нецелесообразно использовать для матриц 3×3, но я предлагаю рассмотреть суть методов на простом примере. Воспользуемся матрицей, для которой мы уже считали определитель — нам будет проще проверить правильность вычислений:

Используя 7-е свойство определителя, вычтем из второй строки третью, умноженную на 2:

из третьей строки вычтем соответствующие элементы первой строки определителя, умноженные на 3:

далее из третьей строки мы вычтем вторую строку, умноженную на -3:

Так как элементы определителя, расположенные под его главной диагональю, равны 0, то, следовательно, определитесь равен произведению элементов, расположенных на главной диагонали:

Как видим, ответ совпал с полученными ранее.

Давайте вспомним формулу определителя матрицы:

Детерминант — это сумма алгебраических дополнений, умноженная на члены одной из строк или одного из столбцов.

Если в результате преобразований мы сделаем так, что одна из строк (или столбец) будет состоять полностью из нулей кроме одной позиции, то нам не нужно будет считать все алгебраические дополнения, поскольку они заведомо будут равны нулю. Как и предыдущий метод, этот целесообразно применять для матриц больших размеров.

Покажем пример на той же самой матрице:

Замечаем, что второй столбец определителя уже содержит один нулевой элемент. Прибавляем к элементам второй строки элементы первой строки, умноженные на -1. Получим:

Вычислим определитель по второму столбцу. Нам нужно посчитать только одно алгебраическое дополнение, поскольку остальные заведомо сводятся к нулю:

Как быстро вычислить определитель третьего порядка?

Для вычисления определителя третьего порядка используют правило треугольника (или «звездочки»).

1. Перемножаем элементы главной диагонали: det(A)=11*22*33…

2. К полученному произведению прибавляем произведение «треугольников с основаниями, параллельными главной диагонали»: det(A)=11*22*33+31*12*23+13*21*32…

3. Все, что связано с побочной диагональю, берем со знаком «-«. Перемножаем элементы побочной диагонали и вычитаем: det(A)=11*22*33+31*12*23+13*21*32-13*22*31…

4. Аналогично «главным треугольникам» перемножаем побочные и вычитаем: det(A)=11*22*33+31*12*23+13*21*32-13*22*31-11*23*32-33*12*21.

det(A)=11*22*33+31*12*23+13*21*32-13*22*31-11*23*32-33*12*21=
=7986+8556+8736-8866-8096-8316=0

Как найти ранг матрицы?

Знание ранга матрицы повысит ваш ранг =)

Что такое ранг матрицы?

В юмористическом эпиграфе статьи содержится большая доля истины. Само слово «ранг» у нас обычно ассоциируется с некоторой иерархией, чаще всего, со служебной лестницей. Чем больше у человека знаний, опыта, способностей, блата и т.д. – тем выше его должность и спектр возможностей. Выражаясь по молодёжному, под рангом подразумевают общую степень «крутизны».

И братья наши математические живут по тем же принципам. Выведем на прогулку несколько произвольных нулевых матриц:

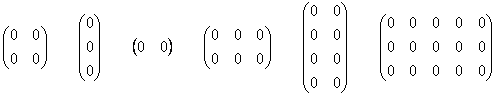
Задумаемся, если в матрице одни нули, то о каком ранге может идти речь? Всем знакомо неформальное выражение «полный ноль». В обществе матриц всё точно так же:

Ранг нулевой матрицы

любых размеров равен нулю

Примечание: нулевая матрица обозначается греческой буквой «тета»

В целях лучшего понимания ранга матрицы здесь и далее я буду привлекать на помощь материалы аналитической геометрии. Рассмотрим нулевой вектор

аффинного базисаматрицу(в указанном геометрическом смысле)

Теперь рассмотрим несколько ненулевых векторов-столбцов и векторов-строк:

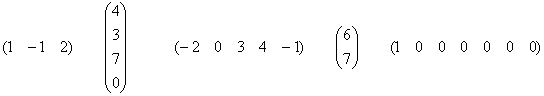
Ранг любого ненулевого вектора-строки (вектора-столбца) равен единице

И вообще – если в матрице произвольных размеров есть хотя бы один ненулевой элемент, то её ранг не меньше единицы.

Алгебраические векторы-строки и векторы-столбцы в известной степени абстрактны, поэтому снова обратимся к геометрической ассоциации. Ненулевой вектор

базиса

Теоретическая справка: в линейной алгебре вектор – это элемент векторного пространства (определяемое через 8 аксиом), который, в частности, может представлять собой упорядоченную строку (или столбец) действительных чисел с определёнными для них операциями сложения и умножения на действительное число. С более подробной информацией о векторах можно ознакомиться в статье Линейные преобразования.

Рассмотрим матрицу

линейно зависимы
трёхмерного базиса

Перепишем координаты векторов в столбцы (транспонируем матрицу):

Что изменилось с точки зрения ранга? Ничего. Столбцы пропорциональны, значит, ранг равен единице

Кстати, обратите внимание, что все три строки тоже пропорциональны. Их можно отождествить с координатами трёх коллинеарных векторов плоскости, из которых только один полезен для построения «плоского» базиса

И это полностью согласуется с нашим геометрическим смыслом ранга.

Из вышеприведённого примера следует важное утверждение:

Ранг матрицы по строкам равен рангу матрицы по столбцам. Об этом я уже немного упоминал на уроке об эффективных методах вычисления определителя.

Примечание: из линейной зависимости строк следует линейная зависимость столбцов (и наоборот). Но в целях экономии времени, да и в силу привычки я почти всегда буду говорить о линейной зависимости строк.

Продолжим дрессировать нашего любимого питомца. Добавим в матрицу третьей строкой координаты ещё одного коллинеарного вектора

Помог ли он нам в построении трёхмерного базиса? Конечно, нет. Все три вектора гуляют туда-сюда по одной дорожке, и ранг матрицы равен единице. Можно взять сколько угодно коллинеарных векторов, скажем, 100, уложить их координаты в матрицу «сто на три» и ранг такого небоскрёба всё равно останется единичным.

Познакомимся с матрицей

линейно независимы

А чему равен ранг матрицы

линейно выразилкомпланарных векторов

Как видите, линейная зависимость в рассмотренной матрице не очевидна, и сегодня мы как раз научимся выводить её «на чистую воду».

Думаю, многие догадываются, что такое ранг матрицы!

Рассмотрим матрицу

линейно независимы
аффинный базис

Как вы знаете, любой четвёртый, пятый, десятый вектор трёхмерного пространства будет линейно выражаться через базисные векторы. Поэтому, если в матрицу

всё равно будет равен трём

Аналогичные рассуждения можно провести для матриц бОльших размеров (понятно, уже без геометрического смысла).

Определение: ранг матрицы – это максимальное количество линейно независимых строк. Или: ранг матрицы – это максимальное количество линейно независимых столбцов. Да, их количество всегда совпадает.

Из вышесказанного также следует важный практический ориентир: ранг матрицы не превосходит её минимальной размерности. Например, в матрице

Обозначения: в мировой теории и практике не существует общепринятого стандарта для обозначения ранга матрицы, наиболее часто можно встретить:

Вычисление определителя для матриц

Определителем порядка n, соответствующим матрице А, называется число, обозначаемое det A и вычисляемое по формуле:

В этой формуле нам всё уже знакомо, давайте теперь посчитаем определитель матрицы для

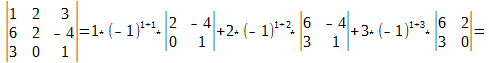
Каков бы ни был номер строки i=1,2,…, n или столбца j = 1, 2,…, n определитель n-го порядка равен сумме произведений элементов этой строки или этого столбца на их алгебраические дополнения, т. е.

Т.е. детерминант можно вычислить по любому столбцу или по любой строке.

Чтобы убедиться в этом, вычислим определитель для матрицы из последнего примера по второму столбцу

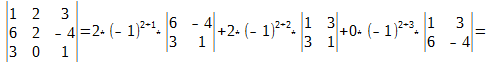
Как видим, результат идентичный и для этой матрицы определитель всегда будет -52 не зависимо от того, по какой строке или по какому столбцу мы его будем считать.

Решение задач

Для закрепления материала в школе и высших учебных заведениях учащимся предлагают выполнить расчёт несколько типовых заданий разной сложности. Умение их решать является доказательством понимания теории. Вот некоторые из них рекомендуемые для самостоятельного решения.

Найти в указанной матрице все определители второго уровня и алгебраические дополнения:

|5 7 3|

|8 5 6|

|6 8 10|

Для решения этой задачи нужно рассматривать первую и вторую строчки. Последовательно убирая строки и столбцы методом вычёркивания, можно получить шесть результатов:

1. M1,2 = |5 6| |8 5| = — 3;
2. ​ M1,3 = |5 3| |8 6| = — 6;
3. M2,3 = |6 3| |5 6| = — 3;
4. A1,2 = (-1)1+2+1+2 * M1,2′ = 9;
5. A1,2 = (-1)1+2+1+3 * M1,3′ = -8;
6. A1,2 = (-1) 1+2+2+3 * M2,3′ = 7.

В следующей задаче рассматривается квадратная матрица три на три, в которой необходимо найти дополнительную характеристику:

(1 2 0)

(-2 0 3)

(3 4 -2)

По условию в таблице имеется девять позиций, для которых можно найти дополнительный элемент. При решении нужно последовательно их все перебрать, вычёркивая соответственные столбцы и строки:

1. M11 = |1 2 | |2 1| = -3;
2. M12 = |0 2| |3 1| = -6;
3. M13 = |0 1 | |3 2| = -3;
4. M21 = |2 -1| |3 1| = -1
5. M22 = |1 -1| |3 1| = 4;
6. M23 = |1 2| |3 2| = -4;
7. M31 = |2 -1| |1 2| = 5;
8. M32 = |1 -1 | |0 2| = -2;
9. M33 = |1 2| |0 1| = -1.

В следующем примере необходимо рассчитать первые три алгебраических дополнения. Пусть дана матрица A:

(1 2 -1)

(0 1 2)

(3 2 1)

Для нахождения первого параметра нужно вычеркнуть первый столбец и строку, при этом для определения знака использовать формулу: A = M (-1) j+i. В итоге получится определитель: A11 = |1 2| |2 1| = 1 — 4 = 3. Знак положительный, так как минус единица будет во второй степени. При этом можно отметить, что далее знак будет попросту чередоваться. Другие вычисления нужно делать аналогично: A12 = |0 2| |3 1| = (-6) * (-1) = 6; A13 = |0 1| |3 2| = -3.

Как видно из примеров, вычисления обычно не вызывают трудностей, но требуют внимательности и усидчивости. Особенно это касается нахождения обратной матрицы. Вычисляется она с помощью алгебраических дополнений, которые равны минорам, умноженным на минус единицу. Довольно часто знаки путают, и в итоге получается неправильный ответ. Поэтому в случае сложных систем есть резон использовать онлайн-калькуляторы.

Свойства определителя матрицы.

• При перестановке местами двух параллельных строк или столбцов определителя его знак меняется на обратный;
• Определитель, содержащий две одинаковых строки или столбца, равен нулю;
• Если одну из строк определителя умножить на какое-либо число, то получится определитель, равный исходному определителю, умноженному на это число;
• При транспонировании матрицы её определитель не меняет своего значения;
• Если в определителе вместо любой строки записать сумму этой строки и любой другой строки, умноженной на некоторое число, то полученный новый определитель будет равен исходному;
• Если каждый элемент какой-либо строки или столбца определителя представляем в виде суммы двух слагаемых, то этот определитель может быть разложен на сумму двух соответствующих определителей;
• Общий множитель элементов какой-либо строки или столбца определителя можно выносить за знак определителя.

Использование интернет-калькулятора

В интернете есть определённая группа сайтов, позволяющая выполнять различные математические вычисления в автоматическом режиме. На их страницах содержится специальный скрипт, выполняющий нахождение минора матрицы онлайн любой сложности. При этом от потребителя не требуется никаких особых знаний, он даже и вовсе может ничего не понимать в алгебраических вычислениях.

Всё, что ему необходимо будет сделать для получения ответа, — это ввести исходные данные в предложенную форму и нажать кнопку «Вычислить». Система автоматически определит нужный алгоритм и, используя свойства матрицы, выведет на экран ответ. При этом, кроме результата, пользователю будет предоставлена возможность ознакомиться с подробным решением.

По отзывам потребителей, из множества таких сервисов можно выделить пять следующих сайтов:

1. Allcalc — сервис с простым интерфейсом, но в то же время позволяющий выполнить любые действия с матрицей, включая нахождение миноров и алгебраических дополнений.
2. Onlinemschool — сайт, умеющий не только быстро выполнять вычисления, но и выводить пошаговое решение с комментариями.
3. MathSemestr — программное обеспечение калькулятора, понимает даже соотношения, взятые из таких популярных программ, как World и Excel.
4. Pikod — бесплатный сайт, предлагающий получить не только ответ, но и подробно расписанный ход решения.
5. Kontrolnaya-rabota — сервис позволяет выполнять любые преобразования матриц, при этом для сложных заданий существует режим «модульный конструктор».

Все указанные сайты доступны на русском языке, бесплатны, имеют простой и понятный интерфейс. На их страницах содержится справочная и теоретическая математическая информация. Кроме неё, для каждого раздела приводится типовой пример с объяснением. Использование онлайн-калькуляторов поможет сэкономить время и научит правильно выполнять действия по вычислению миноров.

Их использование будет полезным не только ученикам или студентам, желающим научиться самостоятельно решать задачи, но и инженерам, выполняющим сложные вычисления. Для специалистов они довольно востребованы, так как при самостоятельном решении небольшая ошибка по невнимательности приведёт к неправильному ответу, что исключено при расчёте в автоматическом режиме.