Векторы

Понятия и определения

По сути, под вектором в математике понимают отрезок с определённой длиной и направлением. Его принято изображать в виде прямой линии, ограниченной двумя точками. Одна из них является началом, а другая концом. Подписывается вектор с помощью двух больших латинских букв или одной маленькой. Числовое значение, соответствующее длине отрезка, является модулем вектора. Изображается модульность двумя вертикальными линиями слева и справа.

Когда начальная и конечная точка отрезка совпадают, вектор называется нулевым. Соответственно, его длина равняется нулю. Кроме этого, векторы, в зависимости от расположения, разделяют на следующие виды:

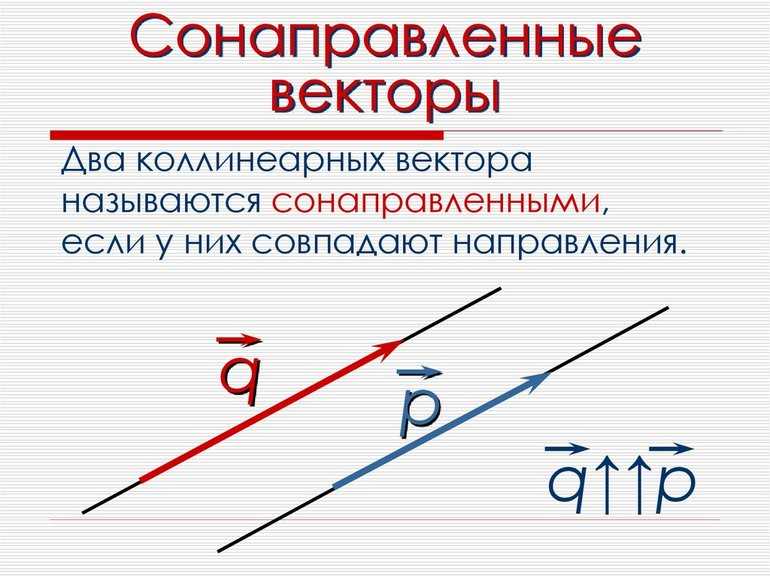
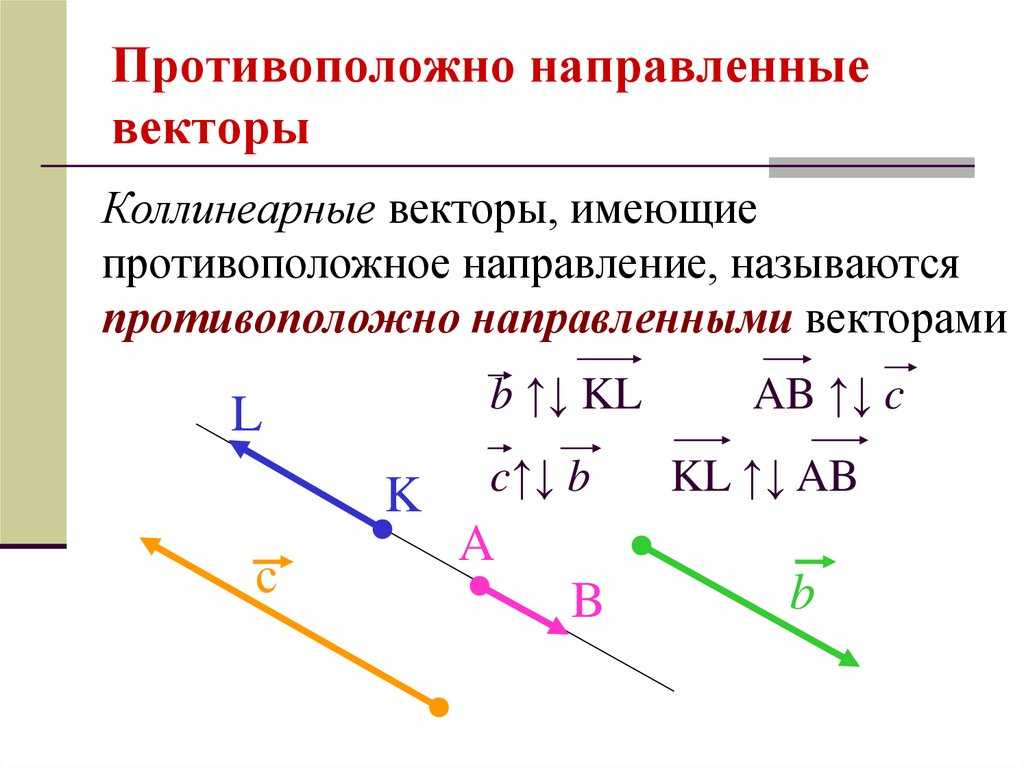
• коллинеарные — отрезки, располагающиеся в пространстве на одной прямой или параллельные одной линии;
• сонаправленные — векторы, совпадающие по направлению;
• противоположные — ограниченные линии, у которых направление является обратным по отношению друг к другу;
• ортогональными — прямые расположены на плоскости так, что создают угол 90 градусов;
• компланарные — отрезки, располагающиеся на одной плоскости, или параллельные;
• равные — прямые, совпадающие по направлению и длине.

Чтобы два вектора можно было назвать коллинеарными, должно выполняться любое из следующих условий:

• для двух отрезков существует число, при котором выполняется равенство a = c * b, где b может быть любым числом;
• координаты векторов равны.

Над векторами можно выполнять арифметические действия. Их можно складывать, вычитать или перемножать. Произведение может быть скалярным, векторным или смешанным. Под первым понимается произведение модулей отрезков на косинус угла, ими образованного, под вторым — площадь параллелограмма, выстроенного на перемножаемых векторах, под третьим — умножение скалярного произведения на векторное.

Линейная зависимость и базис

ортамилюбой вектор трёхмерного пространства можно
представить в виде суммы трёх заранее определённых векторов с зависящими
от этого самого вектора коэффициентами

линейной комбинациейлюбой вектор трёхмерного пространства является линейной комбинацией
векторов

статьёй о
матрицах

любые два вектора на плоскости могут
использоваться в качестве системы координат, если только они не
параллельны

1. каждый вектор интересующего нас пространства должен представляться в
   виде некоторой их линейной комбинации;
2. эта линейная комбинация должна быть единственна, то есть у любого вектора
   должен быть лишь один набор координат, описывающий его.

следующее фундаментальное определениебазисом

базисом

нетривиальнымитривиальной

линейно независимойлинейно зависимой

Линейной оболочкой

эта
линейная оболочка тоже будет являться линейным пространством

• Сумма любых двух векторов из должна лежать в . Проверим это. Пусть у
  нас есть два каких-то вектора и , лежащих в . Раз уж они лежат в ,
  то по определению они равны некоторым линейным комбинациям векторов
  :

  Но тогда, очевидно, их сумма тоже является линейной комбинацией тех же самых
  векторов:

  И тогда, снова по определению , получается, что сумма тоже обязательно
  лежит в .

• Произведение любого вектора на любое число должно лежать в . Тоже, в
  общем-то, довольно очевидный факт: ведь если линейную комбинацию некоторых
  векторов умножить на число, мы получим линейную комбинацию этих же векторов
  с коэффициентами, умноженными на это число.
• В пространстве должен лежать нулевой вектор. И он лежит, ведь он равен
  тривиальной линейной комбинации векторов .
• Для любого вектора в должен лежать вектор , обратный по
  сложению, то есть такой, что . Если заметить, что
  такой вектор всегда равен вектору , то видно, что он лежит в по
  причине, описанной в предпредыдущем пункте.

линейными подпространствами

базисом

Базис в пространстве, на плоскости и на прямой

Определение 4. Базисом в пространстве называется упорядоченная тройка некомпланарных векторов.

Определение 5. Базисом на плоскости называется пара неколлинеарных векторов, взятых в определенном порядке.

Определение 6. Базисом на прямой называется любой ненулевой вектор на этой прямой.

Определение 7. Пусть — базис в пространстве. Если

,

то говорят, что вектор разложен по базису. Числа называются координатами вектора в этом базисе. Аналогично определяются координаты на плоскости и на прямой.

Предложение 7.

1. Каждый вектор, параллельный какой-либо прямой, может быть разложен по базису на этой прямой.
2. Каждый вектор, параллельный какой-либо плоскости, может быть разложен по базису на этой плоскости.
3. Каждый вектор может быть разложен по базису в пространстве.

Координаты вектора в каждом случае определяются однозначно.

Предложение 8. При сложении векторов складываются их соответствующие координаты. При умножении вектора на число все его координаты умножаются на это число.

Критерии линейной зависимости и линейной независимости систем векторов

Система векторов векторного пространства линейно зависима только в том случае, когда один из векторов системы можно выразить через остальные векторы данной системы.

Пусть система e 1 , e 2 , . . . , e n является линейно зависимой. Запишем линейную комбинацию этой системы равную нулевому вектору:

a 1 e 1 + a 2 e 2 + . . . + a n e n = 0

в которой хотя бы один из коэффициентов комбинации не равен нулю.

Пусть a k ≠ 0 k ∈ 1 , 2 , . . . , n .

Делим обе части равенства на ненулевой коэффициент:

a k — 1 ( a k — 1 a 1 ) e 1 + ( a k — 1 a k ) e k + . . . + ( a k — 1 a n ) e n = 0

— a k — 1 a m , где m ∈ 1 , 2 , . . . , k — 1 , k + 1 , n

β 1 e 1 + . . . + β k — 1 e k — 1 + β k + 1 e k + 1 + . . . + β n e n = 0

или e k = ( — β 1 ) e 1 + . . . + ( — β k — 1 ) e k — 1 + ( — β k + 1 ) e k + 1 + . . . + ( — β n ) e n

Отсюда следует, что один из векторов системы выражается через все остальные векторы системы. Что и требовалось доказать (ч.т.д.).

e k = γ 1 e 1 + . . . + γ k — 1 e k — 1 + γ k + 1 e k + 1 + . . . + γ n e n

Переносим вектор e k в правую часть этого равенства:

0 = γ 1 e 1 + . . . + γ k — 1 e k — 1 — e k + γ k + 1 e k + 1 + . . . + γ n e n

Поскольку коэффициент вектора e k равен — 1 ≠ 0 , у нас получается нетривиальное представление нуля системой векторов e 1 , e 2 , . . . , e n , а это, в свою очередь, означает, что данная система векторов линейно зависима. Что и требовалось доказать (ч.т.д.).

• Система векторов является линейно независимой, когда ни один из ее векторов нельзя выразить через все остальные векторы системы.
• Система векторов, которая содержит нулевой вектор или два равных вектора, линейно зависима.

Общие условия линейной зависимости векторов

Определение 1. Векторы , , . называются линейно зависимыми, если найдутся такие вещественные числа , из которых хотя бы одно отлично от нуля, что линейная комбинация векторов , , . с указанными числами обращается в нуль, т.е. имеет место равенство

Векторы , , . , не являющиеся линейно зависимыми, будем называть линейно независимыми.

Определение 2. Векторы , , . называются линейно независимыми, если равенство нулю их линейной комбинации возможно лишь в случае, когда все числа равны нулю.

Теорема 1. Если хотя бы один из векторов , , . является нулевым, то эти векторы являются линейно зависимыми.

Теорема 2. Если среди n векторов какие-либо (n — 1) векторов линейно зависимы, то и все n векторов линейно зависимы.

Определение линейной зависимости векторов

Линейная комбинация векторов – это вектор, заданный выражением , где – коэффициенты.

Представленная комбинация может быть:

• Тривиальная – все коэффициенты равняются нулю.
• Нетривиальная – хотя бы один из коэффициентов не равен нулю.

Векторы a ₁, …, a _n линейно независимы, если только их тривиальная комбинация равна нулевому вектору. То есть:

a ₁, …, a _n линейно независимы, если , исключительно когда .

Векторы a ₁, …, a _n линейно зависимы, если есть такая их нетривиальная комбинация, которая равняется нулевому вектору.

Свойства линейно зависимых векторов

• Линейно зависимые векторы в двух/трехмерном пространстве коллинеарны. Справедливо и обратное утверждение.
• В трехмерном пространстве три линейно зависимых вектора компланарны. Утверждение верно и в обратную сторону.

Линейные комбинации трёх векторов

Определение. Векторы называются компланарными, если они лежат либо в одной плоскости, либо в параллельных плоскостях.

Теорема 4. Необходимым и достаточным условием линейной зависимости трёх векторов является их компланарность.

Следствие 1. Каковы бы ни были неколлинеарные векторы и , для любого вектора , лежащего в одной плоскости с векторами и , найдутся такие вещественные числа и , что справедливо равенство

Следствие 2. Если векторы , и не компланарны, то они линейно независимы.

Следствие 3. Среди трёх некомпланарных векторов не может быть двух коллинеарных векторов и не может быть ни одного нулевого вектора (иначе эти векторы оказались бы линейно зависимыми).

Условия компланарности и линейная зависимость векторов

Среди условий компланарности векторов встречается понятие линейной зависимости, которое следует разобрать перед тем, как перейти непосредственно к условиям.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Линейная зависимость

Линейно зависимыми называются вектора \(\overline{a_1},\;\overline{a_2},\;\dots\;,\;\overline{a_n}\;\), которые можно составить в линейную комбинацию, равную нулю: \(\lambda_1\cdot\overline{a_1}+\;\lambda_2\cdot\overline{a_2}+\dots+\;\lambda_n\overline{\cdot a_n}\;=0.\)

Линейная комбинация — вектор, составленный из суммы векторов \(\overline{a_1},\;\overline{a_2},\;\dots\;,\;\overline{a_n}\;\) и коэффициентов разложения \(\lambda_{1,}\;\lambda_2,\;\dots\;,\;\lambda_n.\)

Существует пять критериев и свойств линейной зависимости векторов:

1. Хотя бы один из векторов можно представить в виде линейной комбинации других.
2. В n-мерном пространстве любые n+1 векторов линейно зависимы.
3. Хотя бы один из векторов — нулевой.
4. Если часть системы векторов линейно зависимы, то это справедливо и для остальных.
5. Если одна система векторов может быть выражена через другую и содержит больше векторов, то такая система линейно зависима.

Условия компланарности

Для неограниченного числа векторов справедливо следующее: если среди них есть не более двух линейно независимых векторов, то они компланарны.

На практике чаще всего встречаются задачи с тройками векторов. Для них существуют и другие условия компланарности:

1. Если три вектора линейно зависимы, то они компланарны.
2. Смешанное произведение компланарных векторов равняется нулю.

Определение вектора.

Понятие вектора известно из школьного курса, но лучше напомнить основные факты, с ним связанные. Пару точек мы называем упорядоченной, если про эти точки известно, какая из них первая, а какая — вторая.

Определение 1.

Отрезок, концы которого упорядочены, называется направленным отрезком или вектором. Первый из его концов называется началом, второй — концом вектора. К векторам относится и нулевой вектор, у которого начало и конец совпадают.

Направление вектора на рисунке принято обозначать стрелкой, над буквенным обозначением вектора тоже ставится стрелка, например \(\overrightarrow{AB}\) (при этом буква, обозначающая начало, обязательно пишется первой). В книгах буквы, обозначающие векторы, набираются полужирным шрифтом, например \(\boldsymbol{a}\). Нулевой вектор обозначается \(\boldsymbol{0}\).

Расстояние между началом и концом вектора называется его длиной (а также модулем или абсолютной величиной). Длина вектора обозначается |\(\boldsymbol{a}\)| или |\(\overrightarrow{AB}\)|.

Векторы называются коллинеарными если существует такая прямая, которой они параллельны. Векторы компланарны, если существует плоскость, которой они параллельны. Нулевой вектор считается коллинеарным любому вектору, так как он не имеет определенного направления. Длина его, разумеется, равна нулю.

Определение 2.

Два вектора называются равными, если они коллинеарны, одинаково направлены и имеют равные длины.

Из этого определения следует, что, выбрав любую точку \(A’\), мы можем построить (и притом только один) вектор|\(\overrightarrow{A’B’}\)|, равный некоторому заданному вектору |\(\overrightarrow{AB}\)|, или, как говорят, перенести вектор |\(\overrightarrow{AB}\)| в точку А’.

Зависимость векторов и свойства

В линейной алгебре вводится такое понятие, как векторная система. Под ней понимают заданный набор вида a1, a2, …, an. Если в это множество вести свободные коэффициенты, а векторные элементы системы сложить между собой, то получится выражение, являющееся линейной комбинацией рассматриваемого пространства: Ya1 + Ya2 + … + Yan.

Когда все свободные члены системы одновременно равняются нулю, то комбинация называется тривиальной. Но если хотя бы один из коэффициентов отличен от нуля, то множество уже будет нетривиальным. Например, система 0 * a1 + 0 * a2 — тривиальная, a 12 * a1 + 0 * a2 — нетривиальная. Разобравшись в этих терминах, можно дать определение зависимости системы. Так, она может быть двух типов:

• линейно независимая — когда тривиальная комбинация совпадает с нулевым отрезком;
• линейно зависимая — когда одна из нетривиальных комбинаций равняется нулевому отрезку.

Определение зависимости важно в векторной алгебре. Опираясь на него, исследуют размерность и базис пространства

Пусть имеется упорядоченная совокупность действительных или комплексных чисел a1, a2, … ap. Линейная комбинация будет выглядеть следующим образом: u * a1 + u * a2 + … + u * ap. Используя правила сложения и произведения векторов, а также понятие n-мерного массива, справедливо утверждать, что рассматриваемая линейная совокупность будет равняться некому отрезку: u * a1 + u * a2 + … + u * ap = b.

При исследовании системы на зависимость необходимо выполнить её проверку на достаточность признаков. Для этого вначале следует убедиться в том, что число векторов не превышает величины координат (в ином случае делается вывод о линейности), затем проверить систему на содержание нулевых отрезков. Если их нет, то необходимо составить матрицу, строками которой будут уравнения системы. При ранге составленной матрицы меньше p — система линейно зависима.

Свойства зависимых и независимых линейных отрезков:

• Система, содержащая нулевую линию, является линейно зависимой.
• Два одинаковых вектора в системе приводят её к линейной зависимости.
• Если в пространстве существуют два пропорциональных отрезка, то она считается линейно зависимой.
• Система из ограниченных прямых будет только тогда линейно зависимой, когда хотя бы один из отрезков является линейной комбинацией остальных.
• Когда к линейно независимой системе присоединяется отрезок и она превращается в линейно зависимую, то добавляемый вектор можно разложить по существующим прямым системы и только единственным образом.

Решение примеров

На практических занятиях в школе учащимся для закрепления курса учитель предлагает решить несколько типовых заданий. Школьники, решая их, выходят на достаточный уровень понимания темы и видят практическое применение знаниям. Вот некоторые из таких заданий:

• В пространстве размещены четыре вектора: a = {7; 9; 0}, b = {-8; 9; 4}, c = {2; 1; 6}, d = {-1; 8; 5}. Нужно проверить их линейную зависимость. Зная определение, можно утверждать, что отрезки будут линейно зависимыми, так как размерность линий не превышает их число.
• Установить линейную зависимость или доказать, что её нет для ограниченных прямых с координатами a = {1; 1; 1}, b = {1; 2; 0}, c = {0; -1; 1}. Чтобы решить это задание, нужно показать соответствие системы на критерии линейности или установить несоответствие. Для этого необходимо вначале найти значения свободных членов, при которых комбинация отрезков будет равняться нулевому вектору. Уравнение следует представить в виде матрицы. Решить ее проще поможет метод Гаусса. После решения матрицы можно будет установить, что система имеет множество корней. Отсюда следует, что имеется ненулевая комбинация коэффициентов, равная нулевому отрезку, например, a — b + c = 0. А это и подтверждает линейную зависимость.
• Проверить отрезки a = {1; -1; 3}, b = 2; -1; 4}, c = {2; 0; 2} на линейную зависимость. Для решения примера из заданных координат необходимо построить матрицу. Её ранг можно вычислить методом Гаусса. В ответе получится, что её размерность равняется двум. Так как 2 < 3, то заданная система соответствует линейности.

Простые школьные задания довольно просто решать самостоятельно. Но на практике часто исследование векторной системы занимает много времени и требует внимательности при анализе. Всё дело в том, что координатами могут быть дробные числа, работать с которыми не всегда удобно. В таких случаях есть резон использовать так называемые онлайн-калькуляторы.

С их помощью можно быстро и безошибочно проверить набор базисов на линейную зависимость. При этом от пользователя никаких особых знаний не требуется. Необходимо лишь иметь устройство с доступом в интернет, на котором установлен веб-обозреватель. Все действия сводятся к заполнению предложенной формы данными из задачи и нажатием кнопки «Проверить».

Примеры задач на линейную зависимость и линейную независимость векторов:

Вектора будут линейно зависимыми, так как размерность векторов меньше количества векторов.

Решение: Найдем значения коэффициентов при котором линейная комбинация этих векторов будет равна нулевому вектору.

Это векторное уравнение можно записать в виде системы линейных уравнений

	x 1 + x 2 = 0
x 1 + 2 x 2 — x 3 = 0
x 1 + x 3 = 0

Решим эту систему используя метод Гаусса

1 1 0 0 1 2 -1 0 1 0 1 0

из второй строки вычтем первую; из третей строки вычтем первую:

1 1 0 0 1 — 1 2 — 1 -1 — 0 0 — 0 1 — 1 0 — 1 1 — 0 0 — 0

1 1 0 0 0 1 -1 0 0 -1 1 0

из первой строки вычтем вторую; к третей строке добавим вторую:

1 — 0 1 — 1 0 — (-1) 0 — 0 0 1 -1 0 0 + 0 -1 + 1 1 + (-1) 0 + 0

1 0 1 0 0 1 -1 0 0 0 0 0

Данное решение показывает, что система имеет множество решений, то есть существует не нулевая комбинация значений чисел x ₁, x ₂, x ₃ таких, что линейная комбинация векторов a , b , c равна нулевому вектору, например:

а это значит вектора a , b , c линейно зависимы.

Ответ: вектора a , b , c линейно зависимы.

Решение: Найдем значения коэффициентов при котором линейная комбинация этих векторов будет равна нулевому вектору.

Это векторное уравнение можно записать в виде системы линейных уравнений

	x 1 + x 2 = 0
x 1 + 2 x 2 — x 3 = 0
x 1 + 2 x 3 = 0

Решим эту систему используя метод Гаусса

1 1 0 0 1 2 -1 0 1 0 2 0

из второй строки вычтем первую; из третей строки вычтем первую:

1 1 0 0 1 — 1 2 — 1 -1 — 0 0 — 0 1 — 1 0 — 1 2 — 0 0 — 0

1 1 0 0 0 1 -1 0 0 -1 2 0

из первой строки вычтем вторую; к третей строке добавим вторую:

1 — 0 1 — 1 0 — (-1) 0 — 0 0 1 -1 0 0 + 0 -1 + 1 2 + (-1) 0 + 0

1 0 1 0 0 1 -1 0 0 0 1 0

из первой строки вычтем третью; к второй строке добавим третью:

1 — 0 0 — 0 1 — 1 0 — 0 0 + 0 1 + 0 -1 + 1 0 + 0 0 0 1 0

1 0 1 0 0 1 0 0 0 0 1 0

Данное решение показывает, что система имеет единственное решение x ₁ = 0, x ₂ = 0, x ₃ = 0, а это значит вектора a , b , c линейно независимые.

Ответ: вектора a , b , c линейно независимые.

В данной статье мы расскажем:

• что такое коллинеарные векторы;
• какие существуют условия коллинеарности векторов;
• какие существуют свойства коллинеарных векторов;
• что такое линейная зависимость коллинеарных векторов.

Сложение и умножение на число.

Пусть \(A\) и \(B\) — матрицы размеров \(m \times n\). Мы можем сопоставить им третью матрицу \(C\) размеров \(m \times n\), элементы которой \(c_{ij}\) связаны с элементами и матриц \(A\) и \(B\) равенствами
$$
c_{ij}=a_{ij}+b_{ij}\ (i=1, \ldots, m,\ j=1, \ldots, n).\label{ref1}
$$

Определение.

Матрица \(C\), определяемая по \(A\) и \(B\) формулой \eqref{ref1}, называется их суммой и обозначается \(A+B\).

Определение.

Матрица \(C\), элементы которой \(c_{ij}\) равны произведениям элементов \(a_{ij}\) матрицы \(A\) на число \(\alpha\), называется произведением \(A\) на \(\alpha\) и обозначается \(\alpha A\). Мы имеем
$$
c_{ij}=\alpha a_{ij}\ (i=1, \ldots, m,\ j=1, \ldots, n).\label{ref2}
$$

Из свойств сложения и умножения чисел легко вытекает наше первое утверждение.

Утверждение 1.

Для любых матриц \(A, B, C\) и любых чисел \(\alpha\) и \(\beta\) выполнены равенства:

• \(A+B=B+A\),
• \((A+B)+C=A+(B+C)\),
• \(\alpha(A+B)=\alpha A+\alpha B\),
• \((\alpha+\beta)A=\alpha A+\beta A\),
• \((\alpha\beta)A=\alpha(\beta A)\).

Матрица, все элементы которой равны нулю, называется нулевой матрицей. Если \(O\) — нулевая матрица размеров \(m \times n\), то для любой матрицы тех же размеров
$$
A+O=A.\nonumber
$$

Матрицу \((-1)A\) называют противоположной матрице \(A\) и обозначают \(-A\). Она обладает тем свойством, что
$$
A+(-A)=O.\nonumber
$$

Сумма матриц \(B\) и \(-A\) называется разностью матриц \(B\) и \(A\) и обозначается \(B-A\). Мы видим, что сформулированные выше свойства линейных операций с матрицами совпадают со свойствами . Используя линейные операции, мы можем составлять из матриц одинаковых размеров \(A_{1}, \ldots, A_{k}\) и чисел \(\alpha_{1}, \ldots, \alpha_{k}\), выражения вида
$$
\alpha_{1}A_{1}+\ldots+\alpha_{k}A_{k}.\nonumber
$$

Такие выражения называются линейными комбинациями матриц. Если какая-то матрица представлена как линейная комбинация других матриц, то говорят, что она по ним разложена.

Пример 1.

Пусть \(\boldsymbol{p}_{1}, \ldots, \boldsymbol{p}_{k}\), — столбцы одинаковой высоты \(n\). Тогда столбец \(\boldsymbol{q}\) той же высоты по ним разложен, если при некоторых коэффициентах \(\alpha_{1}, \ldots, \alpha_{k}\)
$$
\boldsymbol{q}=\alpha_{1}\boldsymbol{p}_{1}+\ldots+\alpha_{k}\boldsymbol{p}_{k},\nonumber
$$
или, в более подробной записи,
$$
\begin{Vmatrix} q^{1}\\
\vdots\\
q^{n}
\end{Vmatrix}=\alpha_{1}
\begin{Vmatrix} p_{1}^{1}\\
\vdots\\
p_{1}^{n} \end{Vmatrix}+\ldots+\alpha_{k} \begin{Vmatrix} p_{k}^{1}\\
\vdots\\
p_{k}^{n} \end{Vmatrix}.\nonumber
$$
В силу определения линейных операций это матричное равенство равносильно \(n\) числовым равенствам
$$
\begin{matrix}
q^{1}=\alpha_{1}p_{1}^{1}+\ldots+\alpha_{k}p_{k}^{1},\\
\ldots\\
q^{n}=\alpha_{1}p_{1}^{n}+\ldots+\alpha_{k}p_{k}^{n}.
\end{matrix}\nonumber
$$

Конечномерные пространства

конечномерным

основную теорему о линейной
зависимости

1. Масштабирование одного из векторов базиса. Возьмём какое-нибудь число
   и умножим на него какой-нибудь вектор . Полученная система
   векторов будет базисом
   наравне с прежней. Почему? Потому что любой вектор пространства по-прежнему
   будет представим в виде линейной комбинации этих векторов, и по-прежнему
   единственным образом. Действительно, пусть в старом базисе произвольный
   вектор представлялся в виде

   Тогда в новом базисе он будет представляться в виде

   где . И представление это по-прежнему единственно, ведь будь
   их два, представлений в исходном базисе тоже было бы два (достаточно было бы
   умножить -е коэффициенты этих двух представлений на , чтобы получить
   коэффициенты двух представлений того же самого вектора в старом базисе).

2. Прибавление к одному из векторов базиса другого, умноженного на число.
   Возьмём какое-нибудь число (теперь никто не запрещает ему быть нулём,
   хотя случай с нулём тривиален и неинтересен) и вместо вектора
   «подсунем» в базис вектор , остальные векторы оставив
   без изменения. Новая система векторов
   тоже будет базисом.
   Проверим это. Пусть какой-либо вектор представлялся в старом базисе в
   виде

   Тогда в новом базисе он примет вид

   Это несложно проверить, подставив вместо сумму ,
   раскрыв пару скобок и сократив пару слагаемых. Совершенно аналогично можно
   получить представление вектора в прежнем базисе, зная представление в
   новом. Значит, представление в новом базисе всегда существует и всегда
   единственно, как и представление в прежнем базисе.

3. Перестановка двух векторов базиса местами. Ну тут всё очевидно.

основную теорему о
линейной зависимостив любом конечномерном линейном пространстве
все базисы состоят из одного и того же количества векторов

нулевые

если
есть некоторый базис из векторов, то никакого базиса из векторов
существовать не может

основная теорема о линейной зависимости

размерностью

Базис.

Ранее было дано определение . Введем теперь определение базиса.

Определение.

Базисом в векторном пространстве называется упорядоченная линейно независимая система векторов такая, что любой вектор этого пространства по ней раскладывается.

Из доказанной выше сразу вытекает, что

• В нулевом пространстве базиса не существует.
• В одномерном пространстве (на прямой линии) базис состоит из одного ненулевого вектора.
• В двумерном пространстве (на плоскости) базис — упорядоченная пара неколлинеарных векторов.
• В трехмерном пространстве базис — упорядоченная тройка некомпланарных векторов.

Требование упорядоченности означает, что, например, в случае плоскости \(\boldsymbol{a}\), \(\boldsymbol{b}\) и \(\boldsymbol{b}\), \(\boldsymbol{a}\) — два разных базиса.

Так как векторы базиса линейно независимы, коэффициенты разложения по базису для каждого вектора пространства определены однозначно. Они называются компонентами или координатами вектора в этом базисе.

Таким образом, если \(\boldsymbol{e_{1}}\), \(\boldsymbol{e_{2}}\), \(\boldsymbol{e_{3}}\) — базис трехмерного пространства, то по формуле \(\boldsymbol{a} = \alpha_{1}\boldsymbol{e_{1}} + \alpha_{2}\boldsymbol{e_{2}} + \alpha_{3}\boldsymbol{e_{3}}\) каждому вектору сопоставлена единственная упорядоченная тройка чисел \(\alpha_{1}\), \(\alpha_{2}\), \(\alpha_{3}\) и каждой тройке чисел — единственный вектор. Аналогично, вектор на плоскости имеет две компоненты, а на прямой — одну.

Компоненты пишутся в скобках после буквенного обозначения вектора, например \(\boldsymbol{a}\)(1,0,1).

В аналитической геометрии геометрические рассуждения о векторах сводятся к вычислениям, в которых участвуют компоненты этих векторов. Следующее предложение показывает, как производятся линейные операции над векторами, если известны их компоненты.

Утверждение 5.

При умножении вектора на число все его компоненты умножаются на это число. При сложении векторов складываются их соответствующие компоненты.

Действительно, если \(\boldsymbol{a} = \alpha_{1}\boldsymbol{e_{1}} + \alpha_{2}\boldsymbol{e_{2}} + \alpha_{3}\boldsymbol{e_{3}}\), то

$$
\lambda\boldsymbol{a} = \lambda(\alpha_{1}\boldsymbol{e_{1}} + \alpha_{2}\boldsymbol{e_{2}} + \alpha_{3}\boldsymbol{e_{3}}) = (\lambda\alpha_{1})\boldsymbol{e_{1}} + (\lambda\alpha_{2})\boldsymbol{e_{2}} + (\lambda\alpha_{3})\boldsymbol{e_{3}}.\nonumber
$$
Если \(\boldsymbol{a} = \alpha_{1}\boldsymbol{e_{1}} + \alpha_{2}\boldsymbol{e_{2}} + \alpha_{3}\boldsymbol{e_{3}}\) и \(\boldsymbol{b} = \beta_{1}\boldsymbol{e_{1}} + \beta_{2}\boldsymbol{e_{2}} + \beta_{3}\boldsymbol{e_{3}}\), то

$$
\boldsymbol{a} + \boldsymbol{b} = (\alpha_{1}\boldsymbol{e_{1}} + \alpha_{2}\boldsymbol{e_{2}} + \alpha_{3}\boldsymbol{e_{3}}) + (\beta_{1}\boldsymbol{e_{1}} + \beta_{2}\boldsymbol{e_{2}} + \beta_{3}\boldsymbol{e_{3}}) =\\= (\alpha_{1} + \beta_{1})\boldsymbol{e_{1}} + (\alpha_{2} + \beta_{2})\boldsymbol{e_{2}} + (\alpha_{3} + \beta_{3})\boldsymbol{e_{3}}.\nonumber
$$

Для одномерного и двумерного пространств доказательство отличается только числом слагаемых.

Линейная зависимость и независимость векторов

Рассмотрим далее основополагающие в линейной алгебре понятие о линейной зависимости и независимости векторов, а также определение базиса системы векторов.

Любую конечную последовательность векторов Будем называть системой векторов, а любую ее подпоследовательность – подсистемой векторов. Линейной комбинацией векторов назовем вектор , равный сумме произведений произвольных чисел на векторы системы, т. е. .

Система векторов называется линейно независимой, если их линейная комбинация равна нулевому вектору только в том случае, когда все числа равны нулю. В обратном случае система векторов называется линейно зависимой. Отсюда, система векторов является линейно зависимой в том случае, когда линейная комбинация векторов равна нулевому вектору, а хотя бы один числовой коэффициент отличен от нуля.

Линейная зависимость и независимость есть свойства системы векторов. Однако часто соответствующие прилагательные относят и к самим векторам. Поэтому вместо «линейно независимая система векторов» допустимо говорить «линейно независимые векторы».

Например, двумерные арифметические векторы И Линейно независимы. Их линейная комбинация равна вектору , который обращается в нулевой вектор Только тогда, когда и .

Если взять векторы И , то они являются линейно зависимыми, так как их линейная комбинация равна нулевому вектору при И , не равных нулю.

Из определения линейной зависимости (независимости) системы векторов вытекают следующие утверждения.

1) Если некоторая система векторов содержит нулевой вектор, то она является линейно зависимой.

Пусть для определенности первый вектор системы является нулевым, т. е.

Тогда линейная комбинация векторов вида равна нулевому вектору, что и доказывает наше утверждение.

2) Если среди векторов системы есть такие, которые сами образуют линейно зависимую подсистему, то вся система также линейно зависима.

Так как исходная подсистема линейно зависима, то среди коэффициентов линейной комбинации векторов подсистемы имеется хотя бы один отличный от нуля. Добавим к этой линейной комбинацию линейную комбинацию векторов, не вошедших в исходную подсистему, с числовыми коэффициентами, равными нулю. Мы получим линейную комбинацию из векторов полной системы, которая равна нулевому вектору, причем имеется хотя бы один коэффициент отличный от нуля. Таким образом, наше утверждение доказано.

3) Если система векторов линейно независима, то и любая ее подсистема также линейно независима.

Если предположить обратное, т. е. существование некоторой линейно зависимой подсистемы, то по предыдущему утверждению отсюда следует зависимость исходной системы, что противоречит условию доказываемой теоремы. Полученное противоречие доказывает сформулированное утверждение.

4) Для того чтобы система из Ненулевых векторов была линейно зависима необходимо и достаточно, чтобы хотя бы один из векторов системы мог быть представлен как линейная комбинация предшествующих векторов.

Необходимость. Пусть система векторов линейно зависима. Тогда равенство выполняется при том условии, что хотя бы одно из чисел в левой части равенства отлично от нуля. Будем перебирать эти числа, начиная с большего номера, и остановимся на некотором номере таком, что соответствующий коэффициент отличен от нуля, т. е. . Номер не может быть равен единице, так как иначе из условий И теоремы о нулевом произведении следовало бы равенство , что противоречит правилу выбора номера и условию теоремы. Таким образом , и справедливо равенство. Отсюда находим вектор Таким образом, чтобы он является линейной комбинацией предшествующих ему векторов, а именно .

Достаточность. Пусть имеется некоторый вектор , который представлен в виде линейной комбинации предшествующих ему векторов . Тогда выполняется условие , что по определению означает линейную независимость исходной системы векторов.

По аналогичной схеме доказывается следующее утверждение.

5) Система векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов системы может быть представлен в виде линейной комбинации остальных векторов.

Как найти подсистему системы векторов

1.4. РАНГ СИСТЕМЫ ВЕКТОРОВ

Рассмотрим систему векторов (1.1), где . Максимальной линейно независимой подсистемой системы векторов (1.1) называется любой набор векторов последней, удовлетворяющий следующим условиям: векторы этого набора линейно независимы; всякий вектор из системы (1.1) линейно выражается через векторы этого набора. В общем, система векторов (1.1) может иметь несколько разных максимальных линейно независимых подсистем.

Теорема 1. 6. Все максимальные линейно независимые подсистемы данной системы векторов содержат одно и то же число векторов.

Число векторов в максимальной линейно независимой подсистеме системы векторов (1.1) называется рангом последней. Системы векторов (1.1) и (1.2) называются эквивалентными, если векторы системы (1.1) линейно выражаются через систему векторов (1.2) и наоборот.

Теорема 1. 7. Ранги эквивалентных систем векторов равны.

Операции, переводящие систему векторов (1.1) в систему, ей эквивалентную, следующие:

1) изменение нумерации векторов в системе;

2) удаление нулевого вектора;

3) удаление вектора, являющегося линейной комбинацией остальных векторов системы;

4) умножение произвольного вектора системы на любое, не равное нулю число;

5) прибавление к одному из векторов системы линейной комбинации остальных векторов системы.

Линейная зависимость векторов и её связь с линейной комбинацией векторов

Чтобы понять, что такое линейная зависимость векторов, введём понятие линейной комбинации векторов.

Линейная комбинация — это сумма векторов, умноженных на некоторые числа. Эти векторы могут иметь разное направление.

То есть, линейная комбинация — это выражение вида

где — какие угодно вещественные числа.

На рисунке сверху — линейная комбинация, представленная вектором , являющимся суммой векторов и , умноженных соответственно на 2 и 3.

Векторы являются линейно зависимыми, если их линейная комбинация равна нулю и хотя бы один из коэффициентов линейной комбинации отличен от нуля.

Линейные комбинации векторов

Определение 1. Линейной комбинациейвекторов называется этих векторов на произвольные вещественные числа, то есть выражения вида

,

где — любые вещественные числа.

Определение 2. Векторы называются линейно зависимыми, если найдутся такие вещественные числа , из которых хотя бы одно отлично от нуля, что линейная комбинация векторов с этими числами обращается в нуль, то есть имеет место равенство:

.

Определение 3. Векторы называются линейно независимыми, если равенство нулю их линейной комбинации возможно лишь в случае, когда все числа равны нулю.

Предложение 1. Если хотя бы один из векторов нулевой, то эти векторы являются линейно зависимыми.

Предложение 2. Если среди векторов какие-либо векторов являются линейно зависимыми, то и все векторов являются линейно зависимыми.

Предложение 3. Система векторов линейно зависима тогда и только тогда, когда один из них представим в виде линейной комбинации остальных.

Обобщение понятия «линейная зависимость» можно посмотреть в соответствующей статье.