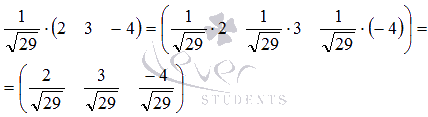Матрицы: примеры с решением и объяснением

Определение.

Определение.

Мы будем называть матрицей размеров \(m \times n\) совокупность \(mn\) чисел, расположенных в виде таблицы из \(m\) строк и \(n\) столбцов:
$$
\begin{Vmatrix}
a_{1}^{1}& a_{2}^{1}& \ldots & a_{n}^{1}\\
a_{1}^{2}& a_{2}^{2}& \ldots & a_{n}^{2}\\
\ldots&\ldots&\ldots&\ldots\\
a_{1}^{m}& a_{2}^{m}& \ldots& a_{n}^{m}
\end{Vmatrix}\nonumber
$$
Числа, составляющие матрицу, мы будем называть элементами матрицы. Если число строк в матрице равно числу столбцов, то матрица называется квадратной, а число строк — её порядком. Остальные матрицы носят название прямоугольных.

Можно дать и такое определение матрицы. Рассмотрим два множества целых чисел \(I={1, 2, \ldots, m}\) и \(J={1, 2, \ldots, n}\). Через \(I \times J\) обозначим множество всех пар вида \((i, j)\), где \(i \in I\), a \(j \in J\). Матрицей называется числовая функция на \(I \times J\), то есть закон, сопоставляющий каждой паре \((i, j)\) некоторое число \(a_{j}^{i}\).

Для читателя, знакомого с программированием, заметим, что матрица — это в точности то же, что и двумерный массив.

Две матрицы называются равными, если они имеют одинаковые размеры, и равны их элементы, стоящие на одинаковых местах.

Рассматривая произвольные матрицы, мы будем обозначать их элементы буквами с двумя индексами. Если оба индекса расположены внизу, то первый из них обозначает номер строки, а второй — номер столбца; если один из индексов расположен сверху, как в написанной выше матрице, то этот индекс обозначает номер строки. Не следует путать верхние индексы с показателями степени.

Матрицу размеров \(1 \times n\), состоящую из одной строки, мы будем называть строкой длины \(n\) или просто строкой. Матрицу размеров \(m \times 1\) называют столбцом высоты \(m\) или просто столбцом. Столбцы и строки мы будем обозначать полужирными буквами.

Часто бывает удобно записывать матрицу как столбец из строк или как строку из столбцов. Пусть
$$
\boldsymbol{a}_{1}=\begin{Vmatrix}
a_{1}^{1}\\
a_{1}^{2}\\
\vdots\\
a_{1}^{m}
\end{Vmatrix},\ \boldsymbol{a}_{2}=\begin{Vmatrix}
a_{2}^{1}\\
a_{2}^{2}\\
\vdots\\
a_{2}^{m}
\end{Vmatrix},\ \ldots,\ \boldsymbol{a}_{n}=\begin{Vmatrix}
a_{n}^{1}\\
a_{n}^{2}\\
\vdots\\
a_{n}^{m}
\end{Vmatrix}.\nonumber
$$
Тогда написанную в начале матрицу можно записать в виде
$$
\begin{Vmatrix}
\boldsymbol{a}_{1}& \boldsymbol{a}_{2}& \ldots& \boldsymbol{a}_{n}
\end{Vmatrix}.\nonumber
$$
Аналогично, если \(\boldsymbol{a}^{1}=\begin{Vmatrix} a_{1}^{1}& \ldots& a_{n}^{1} \end{Vmatrix}, \ldots, \boldsymbol{a}^{m}=\begin{Vmatrix} a_{1}^{m}& \ldots& a_{n}^{m} \end{Vmatrix}\) а же матрица записывается в виде
$$
\begin{Vmatrix}
\boldsymbol{a}^{1}\\
\vdots\\
\boldsymbol{a}^{m}
\end{Vmatrix}.\nonumber
$$

Рассмотрим матрицу \(A\) размеров \(m \times n\) и выберем какие-нибудь \(r\) номеров строк \(i_{1}, \ldots, i_{r}\) и \(s\) номеров столбцов \(j_{1}, \ldots, j_{s}\), причем будем предполагать, что номера выбраны в порядке возрастания: \(i_{1} < i_{2} < \ldots < i_{r}\) и \(j_{1} < j_{2} < \ldots < j_{s}\). Матрицу \(A’\) размеров \(r \times s\), составленную из элементов \(A\), стоящих на пересечении выбранных строк и столбцов, мы назовем подматрицей матрицы \(A\). Итак,
$$
A’=\begin{Vmatrix}
a_{j_{1}}^{i_{1}}& \ldots & a_{j_{s}}^{i_{1}}\\
\ldots&\ldots&\ldots\\
a_{j_{1}}^{i_{r}}& \ldots & a_{j_{s}}^{i_{r}}
\end{Vmatrix}.\nonumber
$$
Если матрица квадратная, то множество тех ее элементов \(a_{i}^{i}\), у которых номер строки равен номеру столбца, называется главной диагональю или просто диагональю матрицы.

Определитель матрицы

Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!

Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу. 

А если матрица три на три? Тут уже посложнее, но справиться можно.

Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.

К счастью, вычислять определители матриц больших размеров на практике приходится редко.

Здесь мы рассмотрели основные операции над матрицами. Конечно, в реальной жизни можно ни разу так и не встретить даже намека на матричную систему уравнений или же наоборот – столкнуться с гораздо более сложными случаями, когда придется действительно поломать голову. Именно для таких случаев и существует профессиональный студенческий сервис. Обращайтесь за помощью, получайте качественное и подробное решение, наслаждайтесь успехами в учебе и свободным временем.

Сложение матриц — теория

Сложение матриц – это алгоритм вычисления новой матрицы С при помощи попарного суммирования соответствующих элементов матриц А и В.

Формула:

(с_{ij} = a_{ij} + b_{ij})

где i – номер строки, а j – номер столбца.

То есть, чтобы получить, например, элемент (с_{11}), нужно сложить (а_{11}) и (b_{11}). 

Когда это возможно, можно ли складывать матрицы разной размерности

Как сложение, так и вычитание матриц возможно только в том случае, когда они равны по размеру.

Также подметим, что нельзя складывать матрицы с обычными целыми числами и дробями. Порядок элементов в таблице менять нельзя.

Определители 2-го и 3-го порядков. Свойства определителей.

Определителем
матрицы
второго
порядка, или определителем

второго порядка, называется число,
которое вычисляется по формуле:

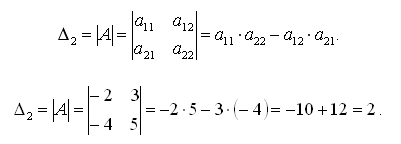
Определителем
матрицы
третьего
порядка, или определителем

третьего порядка, называется число,
которое вычисляется по формуле:

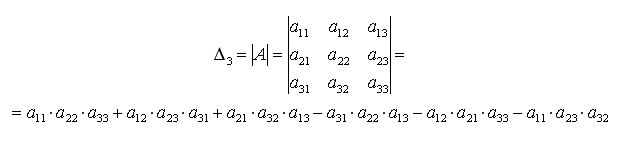
Это
число представляет алгебраическую
сумму, состоящую из шести слагаемых. В
каждое слагаемое входит ровно по одному
элементу из каждой строки и каждого
столбца матрицы
.
Каждое слагаемое состоит из произведения
трех сомножителей.

Знаки,
с которыми члены определителя
матрицы
входят в
формулу нахождения
определителя матрицы

третьего порядка можно определить,
пользуясь приведенной схемой, которая
называется правилом треугольников или
правилом Сарруса. Первые три слагаемые
берутся со знаком плюс и определяются
из левого рисунка, а последующие три
слагаемые берутся со знаком минус и
определяются из правого рисунка.

Определить
количество слагаемых, для нахождения
определителя матрицы
,
в алгебраической сумме, можно вычислив
факториал:
2! = 1 × 2 = 2
3! = 1 × 2 × 3 = 6

Свойства
определителей матриц

Свойства
определителей матриц:

Свойство
№ 1:

Определитель
матрицы

не изменится, если его строки заменить
столбцами, причем каждую строку столбцом
с тем же номером, и наоборот
(Транспонирование).
|А|
= |А| Т

Следствие:

Столбцы
и строки определителя
матрицы
равноправны,
следовательно, свойства присущие строкам
выполняются и для столбцов.

Свойство
№ 2:

При
перестановке 2-х строк или столбцов
определитель матрицы

изменит знак на противоположный, сохраняя
абсолютную величину, т.е.:

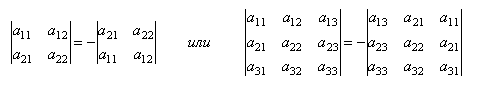
Свойство
№ 3:

Определитель
матрицы
, имеющий два одинаковых ряда,
равен нулю.

Свойство
№ 4:

Общий
множитель элементов какого-либо ряда
определителя матрицы

можно вынести за знак определителя
.

Следствия
из свойств № 3 и № 4:

Если
все элементы некоторого ряда (строки
или столбца) пропорциональны соответствующим
элементам параллельного ряда, то такой
определитель матрицы

равен нулю.

Свойство
№ 5:

определителя
матрицы
равны нулю,
то сам определитель
матрицы
равен нулю.

Свойство
№ 6:

Если
все элементы какой–либо строки или
столбца определителя

представлены в виде суммы 2-х слагаемых,
то определитель

матрицы

можно представить в виде суммы 2-х
определителей

по формуле:

Свойство
№ 7:

Если
к какой–либо строке (или столбцу)
определителя

прибавить соответствующие элементы
другой строки (или столбца), умноженные
на одно и тоже число, то определитель
матрицы
не
изменит своей величины.

Пример
применения свойств для вычисления
определителя матрицы
:

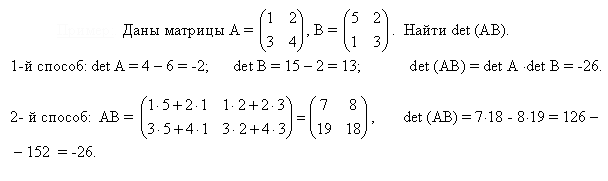
В этой теме будут рассмотрены такие операции, как сложение и вычитание матриц, умножение матрицы на число, умножение матрицы на матрицу, транспонирование матрицы. Все обозначения, которые используются на данной странице, взяты из предыдущей темы .

Нахождение обратной матрицы в Excel

Матрица А-1 называется обратной для матрицы А, если АА-1=А-1А=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).

Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().

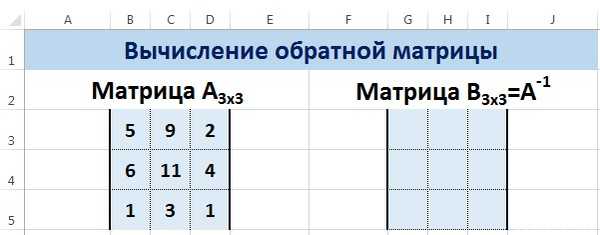
Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.

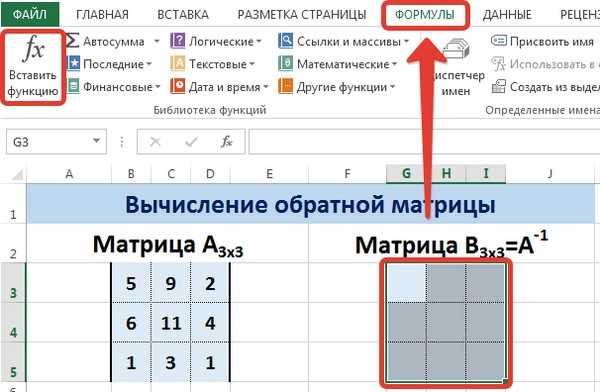
В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.

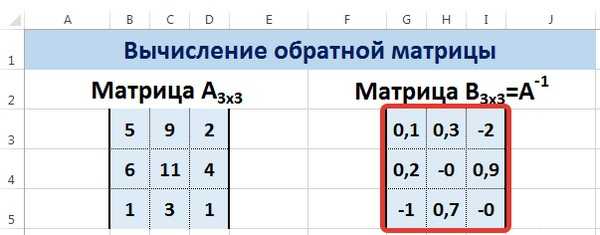
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А-1

Нажмите для увеличения

Мы получили обратную матрицу.

Умножение и деление матрицы на число в Excel

Способ 1

Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.

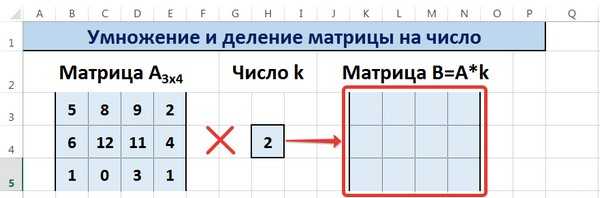
Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а₁₁ матрицы А.

Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.

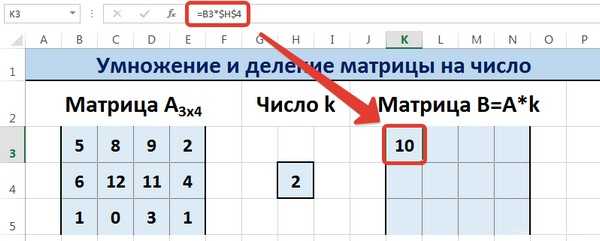
С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.

Таким образом, мы умножили матрицу А в Excel и получим матрицу В.

Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.

Способ 2

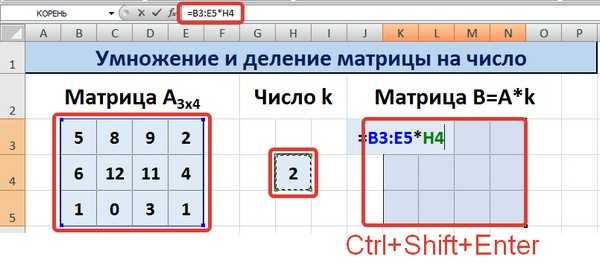
Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.

Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.

 

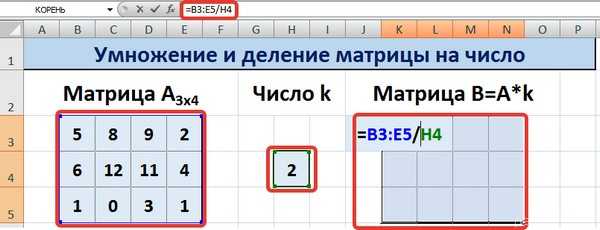
Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/H4, т.е. знак «*» меняем на «/».

Онлайн калькулятор сложения и вычитания матриц

Примеры сложения и вычитания матриц

Сложить или вычесть две матрицы возможно только в том случае, если матрицы одинакового размера.

При сложении или вычитании матриц A и B размерности m × n, получаем матрицу C такойже размерности m × n

b22 = -2
B23 = 7
B31 = 8.98
B32 = 51
B33 = -3

Сложить или вычесть две матрицы возможно только в том случае, если матрицы одинакового размера.

При сложении или вычитании матриц A и B размерности m × n, получаем матрицу C такойже размерности m × n

Сложить или вычесть две матрицы возможно только в том случае, если матрицы одинакового размера.

При сложении или вычитании матриц A и B размерности m × n, получаем матрицу C такойже размерности m × n

Примечание: найти можно только сумму матриц одинакового размера.

Калькулятор сложения матриц – Онлайн калькулятор. Сложение и вычитание матриц.

Наш онлайн калькулятор позволяет найти сумму и разность двух матриц всего в пару кликов. Для того чтобы сложить или вычесть две матрицы выберите размер матриц, введите необходимые значения в поля ввода и нажмите кнопку «Вычислить», калькулятор выдаст ответ и подробное решение! Каждый шаг будет детально расписан, это поможет вам понять, как был получен ответ.

Заполните элементы матриц

Решили сегодня: раз, всего раз

Разность матриц можно представить в виде сложения или умножения матрицы на число.

Свойства сложения матриц

Степени натуральных чисел.

19.04.2019 21:24:52

2019-04-19 21:24:52

Любые данныеЛюбые данныеЛюбые данные Любые данные

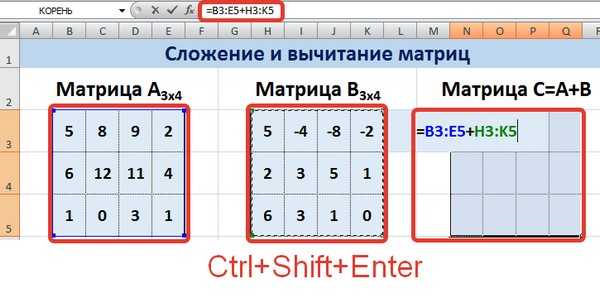
Сложение и вычитание матриц в Excel

Способ 1

Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. с_ij = а_ij + b_ij.

Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+H3, где B3 и H3 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.

С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.

Для вычитания матрицы В из матрицы А (С=А — В) в ячейку N3 введем формулу =B3 — H3 и скопируем её на весь диапазон матрицы С.

Способ 2

Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.

Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.

Возведение матрицы в степень

Среди всех операций умножения отдельного внимания заслуживает возведение в степень — это когда мы несколько раз умножаем один и тот же объект на самого себя. Матрицы — не исключение, их тоже можно возводить в различные степени.

Такие произведения всегда согласованы:

\\cdot \left=\left\]

И обозначаются точно так же, как и обычные степени:

\

На первый взгляд, всё просто. Посмотрим, как это выглядит на практике:

Как видите, ничего сложного в возведении матрицы в степень нет. Последний пример можно обобщить:

\}^{n}}=\left\]

Этот факт легко доказать через математическую индукцию или прямым перемножением. Однако далеко не всегда при возведении в степень можно выловить подобные закономерности. Поэтому будьте внимательны: зачастую перемножить несколько матриц «напролом» оказывается проще и быстрее, нежели искать какие-то там закономерности.

В общем, не ищите высший смысл там, где его нет. В заключение рассмотрим возведение в степень матрицы большего размера — аж $\left$.

Как видите, объём вычислений стал больше, но смысл от этого нисколько не поменялся.:)

На этом урок можно заканчивать. В следующий раз мы рассмотрим обратную операцию: по имеющемуся произведению будем искать исходные множители.

Как вы уже, наверное, догадались, речь пойдёт об обратной матрице и методах её нахождения.

Главные
применения матриц связаны м операцией
умножения.

Даны
две матрицы:

А
– размера mn

B
– размера nk

Т.к.
длина строки в матрице А совпадает с
высотой столбца в матрице В, можно
определить матрицу С=АВ, которая будет
иметь размеры mk.
Элемент
матрицы
С, расположенный в произвольнойi-й
строке (i=1,…,m)
и произвольном j-м
столбце (j=1,…,k),
по определению равен скалярному
проиведению двух векторов из
:i-й
строк марицы А и j-го
столбца матрицы В:

Свойства:

Как
определяется операция умножения матрицы
А на число λ?

Произведением
А на число λ
называется матрица, каждый элемент
которой равен произведению соответствующего
элемента А на λ.
Следствие: Общий множитель всех элементов
матрицы можно выносить за знак матрицы.

Обратные «модели»

Обратная матрица тоже встречается при решении задач. Вырожденная «модель» — это квадратный объект строк и столбцов n-го порядка, когда определитель равен нулю. Невырожденная – когда не равен ему соответственно.

Матрица A-1 – обратная, если для нее актуально соотношение типа: A x A-1=A-1 x A = E.

Если A-1 не вырождена, то существует всего одна обратная матрица A-1. Она будет равна значению:

А вот несколько наглядных примеров:

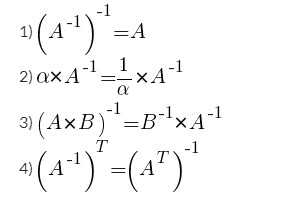
Как найти

Для того, чтобы определить A-1, необходимо:

• Найти детерминант A.
• Проверить, чтобы он не был равен нулю.
• Найти миноры матрицы – M_ij.
• Определить A_ij= (-1)i+jM_ij.
• Построить матрицу алгебраических дополнений:

Поделить каждое из слагаемых (каждый элемент матрицы) объекта на детерминант A.

Умножение числа на матрицу, как и другие операции – это не так трудно. Зная соответствующую базу, человек сможет производить вручную или через специальные калькуляторы необходимые подсчеты. А некоторые видео уроки объяснят теорию простым языком.

А(В + С) = АВ + АС

(А + В)С = АС + ВС.

4) Если произведение АВ определено, то для любого числа

верно соотношение:

(AB

) = (

A

)
B

=
A

(

B

).

5) Если определено произведение АВ, то определено произведение В Т А Т и выполняется равенство:

(АВ) Т = В Т А Т, где

индексом Т обозначается транспонированная
матрица.

6) Заметим также, что для любых квадратных матриц det (AB) = detA

detB.

Что такое det
будет рассмотрено ниже.

Определение

.
Матрицу В называют транспонированной
матрицей А, а переход от А к В транспонированием
, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В.

А = ; В = А Т =;

другими словами, b
ji
= a
ij
.

В качестве следствия из предыдущего свойства (5) можно записать, что:

(ABC
) T
= C
T
B
T
A
T
,

при условии, что определено произведение матриц АВС.

Пример.

Даны матрицы А = , В = , С = и число

= 2. Найти А
Т
В+

С.

A

T

=
;
A

T

B

=


=
=
;

C

=
; А
Т
В+

С =
+
=
.

Пример.
Найти произведение матриц А = и В = .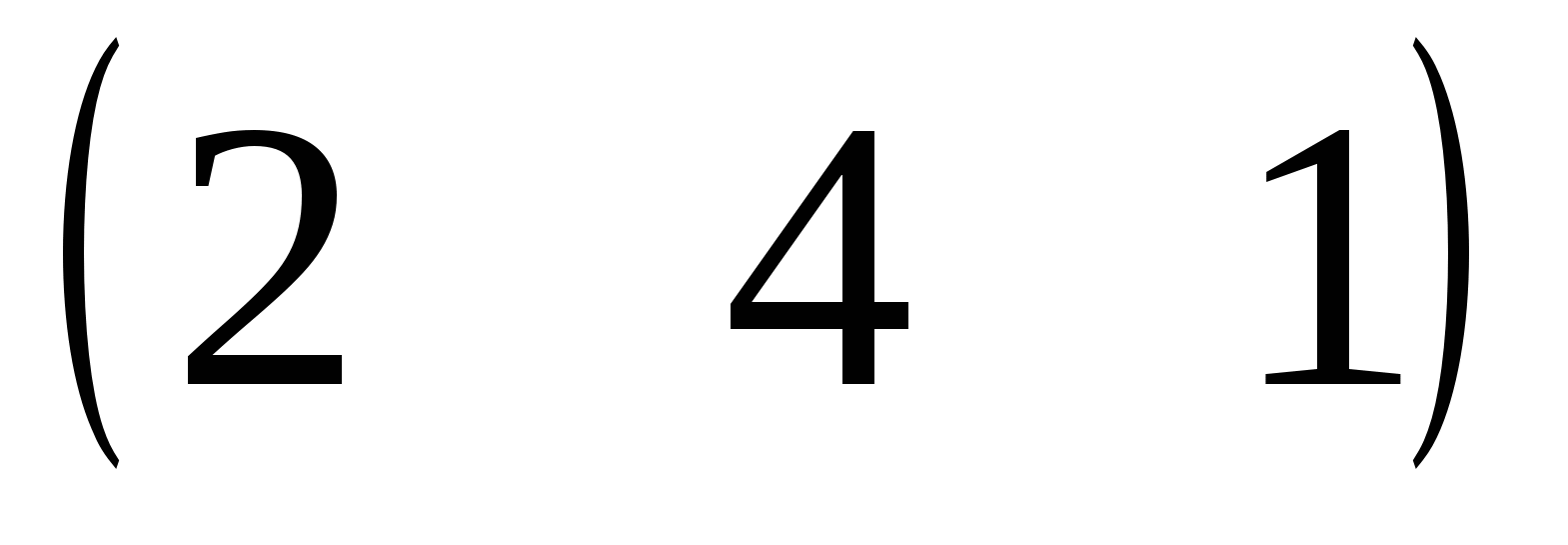

АВ =

= .

ВА = 
= 2

1 + 4

4 + 1

3 = 2 + 16 + 3 = 21.

Пример.
Найти произведение матриц А=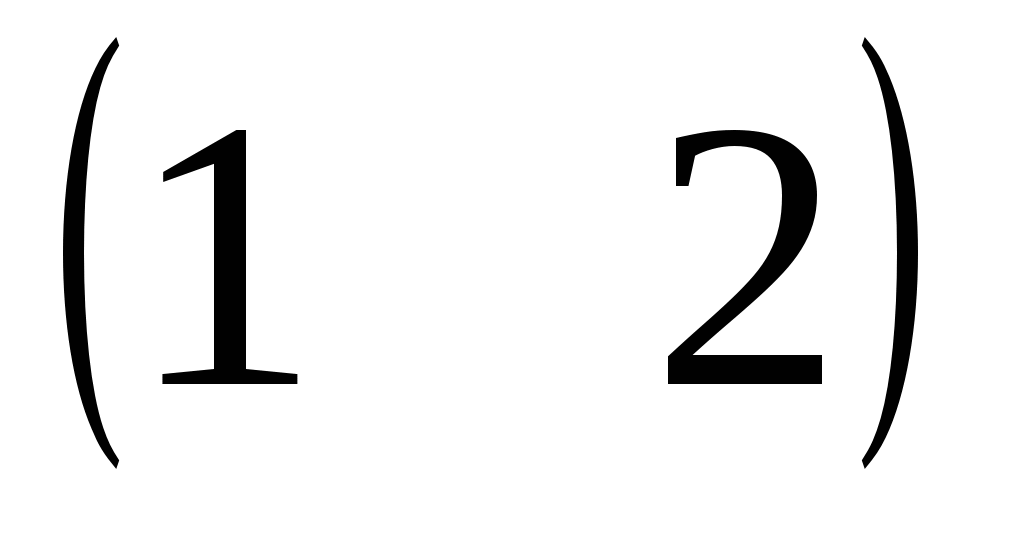, В =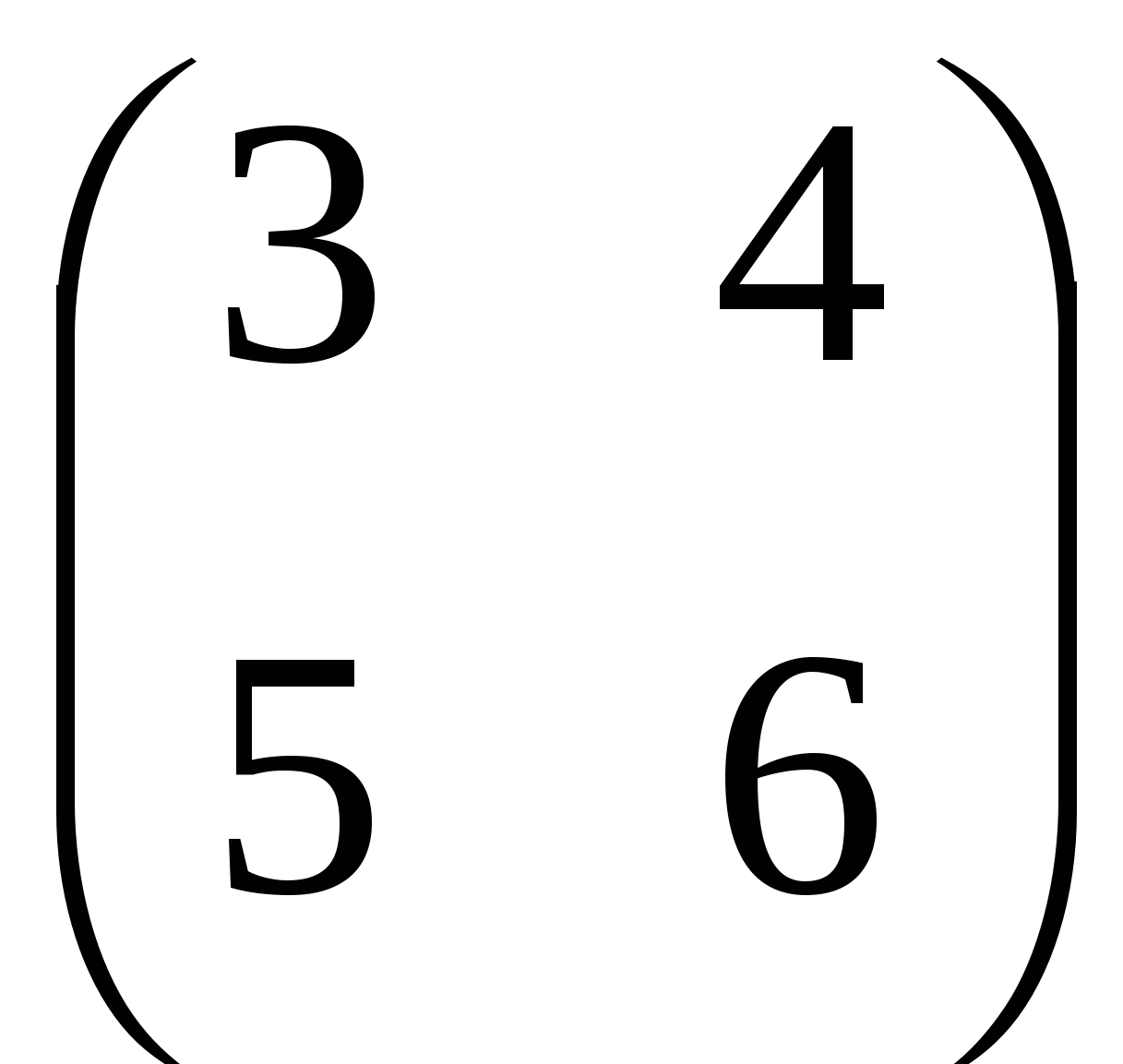

АВ = 
= = .

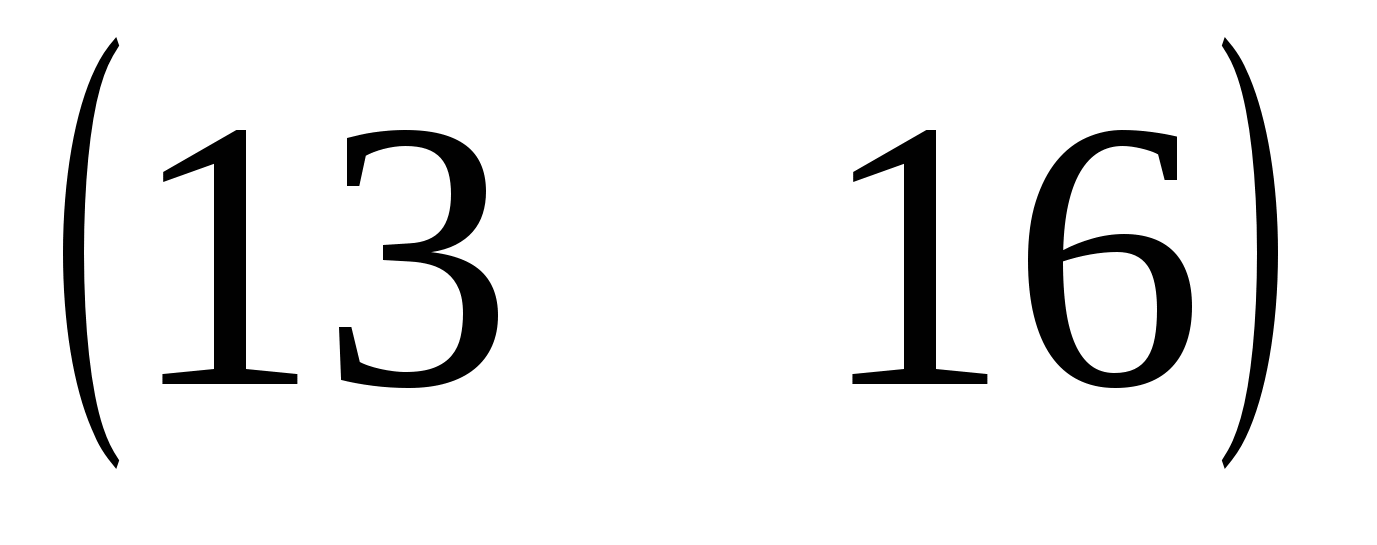Определители
(детерминанты).

Определение.

Определителем
квадратной матрицы А= называется число, которое может быть вычислено по элементам матрицы по формуле:

det
A
= , где (1)

М
1к
– детерминант матрицы, полученной из исходной вычеркиванием первой строки и k
– го столбца

Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.

Формула (1) позволяет вычислить определитель матрицы по первой строке, также справедлива формула вычисления определителя по первому столбцу:

det
A
= (2)

Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула:

detA
= , i
= 1,2,…,n
. (3)

Очевидно, что различные матрицы могут иметь одинаковые определители.

Определитель единичной матрицы равен 1.

Для указанной матрицы А число М 1к называется дополнительным минором
элемента матрицы a
1 k
. Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.

Определение.

Дополнительный минор
произвольного элемента квадратной матрицы a
ij
равен определителю матрицы, полученной из исходной вычеркиванием i
-ой строки и j
-го столбца.

Свойство1.

Важным свойством определителей является следующее соотношение:

det A = det A
T
;

Свойство

2.

det (A



B) = det A



det B.

Свойство 3.

det

(AB

) =
detA



detB

Свойство 4.

Если в квадратной матрице поменять местами какие-либо две строки (или столбца), то определитель матрицы изменит знак, не изменившись по абсолютной величине.

Свойство 5.

При умножении столбца (или строки) матрицы на число ее определитель умножается на это число.

Свойство 6.

Если в матрице А строки или столбцы линейно зависимы, то ее определитель равен нулю.

Определение:

Столбцы (строки) матрицы называются линейно зависимыми
, если существует их линейная комбинация, равная нулю, имеющая нетривиальные (не равные нулю) решения.

Свойство 7.

Если матрица содержит нулевой столбец или нулевую строку, то ее определитель равен нулю. (Данное утверждение очевидно, т.к. считать определитель можно именно по нулевой строке или столбцу.)

Свойство 8.

Определитель матрицы не изменится, если к элементам одной из его строк(столбца) прибавить(вычесть) элементы другой строки(столбца), умноженные на какое-либо число, не равное нулю.

Свойство 9.

Если для элементов какой- либо строки или столбца матрицы верно соотношение:
d

=

d

1



d

2

,

e

=

e

1



e

2

,

f

=
det (AB).

1-й способ: det A = 4 – 6 = -2; det B = 15 – 2 = 13; det (AB) = det A

det B = -26.

2- й способ:
AB

=
,
det

(AB

) = 7


18 — 8


19 = 126 –

– 152 = -26.

1-й курс, высшая математика, изучаем матрицы
и основные действия над ними. Здесь мы систематизируем основные операции, которые можно проводить с матрицами. С чего начать знакомство с матрицами? Конечно, с самого простого — определений, основных понятий и простейших операций. Заверяем, матрицы поймут все, кто уделит им хотя бы немного времени!

Некоторые свойства операций над матрицами.

Здесь предполагается, что $\alpha$, $\beta$ — некоторые числа, а $A$, $B$, $C$ — матрицы. Для первых четырех свойств я указал названия, остальные можно назвать по аналогии с первыми четырьмя.

1. $A+B=B+A$ (коммутативность сложения)
2. $A+(B+C)=(A+B)+C$ (ассоциативность сложения)
3. $(\alpha+\beta)\cdot A=\alpha A+\beta A$ (дистрибутивность умножения на матрицу относительно сложения чисел)
4. $\alpha\cdot(A+B)=\alpha A+\alpha B$ (дистрибутивность умножения на число относительно сложения матриц)
5. $A(BC)=(AB)C$
6. $(\alpha\beta)A=\alpha(\beta A)$
7. $A\cdot (B+C)=AB+AC$, $(B+C)\cdot A=BA+CA$.
8. $A\cdot E=A$, $E\cdot A=A$, где $E$ — единичная матрица соответствующего порядка.
9. $A\cdot O=O$, $O\cdot A=O$, где $O$ — нулевая матрица соответствующего размера.
10. $\left(A^T \right)^T=A$
11. $(A+B)^T=A^T+B^T$
12. $(AB)^T=B^T\cdot A^T$
13. $\left(\alpha A \right)^T=\alpha A^T$

В следующей части будет рассмотрена операция возведения матрицы в целую неотрицательную степень, а также решены примеры, в которых потребуется выполнение нескольких операций над матрицами.

Сложение матриц
$ A $ и $ B $ это арифметическая операция, в результате которой, должна получаться матрица $ C $, каждый элемент которой равен сумме соответствующих элементов складываемых матриц:

$$ c_{ij} = a_{ij} + b_{ij} $$

Более подробно формула сложения двух матриц выглядит так:

$$ A + B = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} + \begin{pmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{pmatrix} = $$

$$ = \begin{pmatrix} a_{11} + b_{11} & a_{12}+b_{12} & a_{13}+b_{13} \\ a_{21}+b_{21} & a_{22}+b_{22} & a_{23}+b_{23} \\ a_{31}+b_{31} & a_{32}+b_{32} & a_{33}+b_{33} \end{pmatrix} = C $$

В формуле складываются матрицы 3 на 3, значит и получиться должна матрица 3 на 3.

Вычитание матриц
полностью аналогично по алгоритму сложения, только знак минус. Каждый элемент искомой матрицы $ C $ получается благодаря вычитанию соответствующих элементов матриц $ A $ и $ B $:

$$ c_{ij} = a_{ij} — b_{ij} $$

Запишем подробную формулу вычитания двух матриц:

$$ A — B = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} — \begin{pmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{pmatrix} = $$

$$ = \begin{pmatrix} a_{11} — b_{11} & a_{12}-b_{12} & a_{13}-b_{13} \\ a_{21}-b_{21} & a_{22}-b_{22} & a_{23}-b_{23} \\ a_{31}-b_{31} & a_{32}-b_{32} & a_{33}-b_{33} \end{pmatrix} = C $$

Будет полезно знать для дальнейших решений задач с матрицами знать свойства сложения (вычитания).

Сумма матриц

Если сложить матрицы A и B одинакового размера, то получится матрица C того же размера, элементы которой равны сумме соответствующих элементов исходных матриц.

Примечание: найти можно только сумму матриц одинакового размера.

Свойства сложения матриц

1. Переместительный закон

2. Асоциативный закон

(A + B) + C = A + (B + C)

3. Если к матрице прибавить нулевую матрицу, она не изменится.

A + Θ = A, где Θ – нулевая матрица.

4. Если из матрицы вычесть ее же, получится нулевая матрица.

Примечание: вычитать также, как и складывать, можно только матрицы одинакового размера.

Разность матриц

Умножение обыкновенных дробей.

26.08.2018 22:50:37

2020-01-26 08:22:04

Любые данныеЛюбые данныеЛюбые данные Любые данные Любые данные

Определение матрицы

Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A

, матрица B

и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m

на n

, где m

– количество строк, а n

– количество столбцов.

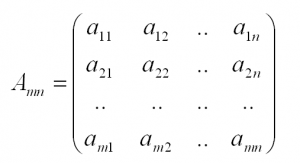
Элементы, для которых i=j

(a11, a22, ..

) образуют главную диагональ матрицы, и называются диагональными.

Что можно делать с матрицами? Складывать/вычитать
, умножать на число
, умножать между собой
, транспонировать
. Теперь обо всех этих основных операциях над матрицами по порядку.

Операция умножения матрицы на число.

Определение операции умножения матрицы на число.

Операция умножения матрицы на число определена ДЛЯ МАТРИЦ ЛЮБОГО ПОРЯДКА.

Определение.

Произведение матрицы и действительного (или комплексного) числа
— это матрица, элементы которой получаются умножением соответствующих элементов исходной матрицы на число , то есть, .

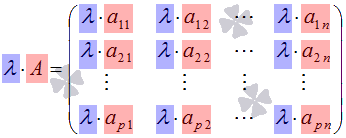
Таким образом, результатом умножения матрицы на число является матрица того же порядка.

Свойства операции умножения матрицы на число.

Из свойств операции умножения матрицы на число следует, что умножение нулевой матрицы на число ноль даст нулевую матрицу, а произведение произвольного числа и нулевой матрицы есть нулевая матрица.

Умножение матрицы на число — примеры и их решение.

Разберемся с проведением операция умножения матрицы на число на примерах.

Пример.

Найдите произведение числа 2
и матрицы .

Решение.

Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число: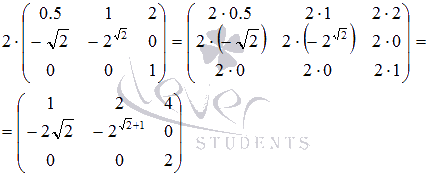

Пример.

Выполните умножение матрицы на число .

Решение.

Умножаем каждый элемент заданной матрицы на данное число: