1.7. Некоторые важные функции
Excel предоставляет широкий выбор стандартных
(встроенных) функций. Мы не можем рассмотреть их все, поэтому
остановимся только на тех, которые представляются нам самыми важными.
SUM/ СУММ
Суммирует все числа в
списке аргументов или в области.
Синтаксис
:
SUM
(number1
)
Пример
Рис.12
Функция SUM
SUMSQ
/ СУММКВ
Возвращает сумму квадратов аргументов.
Синтаксис
:
SUMSQ
(number1
)
Пример
Рис.13
Функция SUM
SQ
SUMPRODUCT / СУММПРОИЗВ
Перемножает соответствующие элементы заданных массивов и
возвращает сумму произведений
Синтаксис
:
SUMPRODUCT
(array1
,
array2
, …)
Пример
Рис.14
Функция SUMPRODUCT
AVERAGE / СРЗНАЧ
VAR
/ ДИСП
STDEV / СТАНДОТКЛОН
CORREL / КОРРЕЛ
Функции можно объединять в
составные формулы, пример которой показан на Рис. 19.
Рис.19 Пример составной формулы
1.7. Некоторые важные функции
Excel предоставляет широкий выбор стандартных
(встроенных) функций. Мы не можем рассмотреть их все, поэтому
остановимся только на тех, которые представляются нам самыми важными.
SUM/ СУММ
Суммирует все числа в
списке аргументов или в области.
Синтаксис:
SUM(number1
)
Пример
Рис.12
Функция SUM
SUMSQ / СУММКВ
Возвращает сумму квадратов аргументов.
Синтаксис:
SUMSQ(number1
)
Пример
Рис.13 Функция SUMSQ
SUMPRODUCT / СУММПРОИЗВ
Перемножает соответствующие элементы заданных массивов и
возвращает сумму произведений
Синтаксис:
SUMPRODUCT (array1,
array2, …)
Пример
Рис.14 Функция SUMPRODUCT
AVERAGE / СРЗНАЧ
Возвращает
своих аргументов
Синтаксис:
AVERAGE(number1
)
Пример
Рис.15 Функция AVERAGE
VAR / ДИСП
Оценивает по выборке .
Синтаксис:
VAR(number1
,number2,
…)
Пример
Рис.16 Функция VAR
STDEV / СТАНДОТКЛОН
Оценивает по выборке
.
Синтаксис:
STDEV(number1
,number2,
…)
Пример
Рис.17 Функция
STDEV
CORREL / КОРРЕЛ
Возвращает
между интервалами
ячеек array1 и array2
Синтаксис:
CORREL(array1,
array2)
Пример
Рис.17 Функция
CORREL
Функции можно объединять в
составные формулы, пример которой показан на Рис. 19.
Рис.19 Пример составной формулы
Решение матриц в Excel
С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число/матрицу; найти обратную матрицу и ее определитель.
Транспонирование
Транспонировать матрицу — поменять местами строки и столбцы.
Сначала отмечаем пустую область, куда будем транспонировать матрицу. В исходном массиве 4 строки — в области транспонирования должно быть 4 столбца. 5 столбцов — это пять строк в пустой области.
- 1 способ. Выберите исходную матрицу. Нажмите «копировать». Выберите пустую область. Клавиша «Развернуть» «Вставить». Откройте специальное меню «Вставить». Выберите операцию «Транспонирование». Закройте диалоговое окно, нажав кнопку OK.
- 2 пути. Выберите ячейку в верхнем левом углу пустой области. Вызов мастера функций. Функция ТРАНСПОЗЕР. Аргумент представляет собой диапазон исходной матрицы.
Нажимаем ОК. Пока функция выдает ошибку. Выберите всю область, в которую вы хотите транспонировать матрицу. Нажмите кнопку F2 (переход в режим редактирования формулы). Нажмите комбинацию клавиш Ctrl+Shift+Enter.
Преимущество второго метода заключается в том, что при изменении исходной матрицы транспонированная матрица изменяется автоматически.
Сложение
Вы можете добавлять массивы с одинаковым количеством элементов. Количество строк и столбцов в первой области должно быть равно количеству строк и столбцов во второй области.
В первую ячейку полученного массива введите формулу вида: = первый элемент первого массива + первый элемент второго: (=B2+H2). Нажмите Enter и разверните формулу на весь диапазон.
Умножение матриц в Excel
Задание:
Чтобы умножить массив на число, необходимо умножить каждый его элемент на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).
Умножьте матрицу на матрицу для разных областей. Произведение матриц можно найти только в том случае, если количество столбцов в первой матрице равно количеству строк во второй.
В полученной матрице количество строк равно количеству строк в первой матрице, а количество столбцов равно количеству столбцов во второй.
Для удобства выделим область, где будут размещены результаты умножения. Делаем первую ячейку получившегося поля активной. Вводим формулу: = МНОЖЕСТВО (А9:С13; Е9:Н11). Введите как формулу массива.
Обратная матрица в Excel
Его имеет смысл найти, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).
Размер обратной матрицы равен размеру исходной. Функция Excel — МОБР.
Выберите первую ячейку в пустой области для обратной матрицы. Введите формулу «=MOBR(A1:D4)» в качестве функции массива. Единственным аргументом является диапазон исходного массива. Получили обратную матрицу в Excel:
2.1. Формулы массива
Многие операции с матрицами выполняются с помощью формул
специального вида, называемыми формулами массива. От других формул они
отличаются тем, что их результатом является не одна величина (число), а
набор величин – массив. При вводе таких формул требуется специальное
подтверждение – вместо клавиши ENTER надо
нажимать комбинацию из трех клавиш CTRL+SHIFT+ENTER.
Поясним использование формул массивов на простом
примере. Предположим, что нам нужно выполнить автошкалирование
(стандартизацию) данных, записанных в матрице X. Для
этого сначала нужно вычислить средние значения mj и
среднеквадратичные отклонения sj для каждого (j-го)
столбца X, а затем вычесть из каждого столбца величину
mjи поделить на величину sj
Такое преобразование можно сделать с помощью обычных формул, как это
показано на Рис. 25.
Рис.25
Обычная формула
Надо только не забыть указать знак $ перед номерами строк
9 (m) и 11
(s) , чтобы зафиксировать положение соответствующих величин в
строках.
Если матрица X велика, то удобнее
воспользоваться формулой массива. (Рис. 26). Назовем соответствующие
области на листе: X,
m и
s. Отметим пустую область
N3:R7, размеры которой совпадают с ожидаемым результатом. После
этого введем в Formula Bar выражение
=(X-m)/s. Завершает ввод комбинация клавиш
CTRL+SHIFT+ENTER. Если все сделано правильно,
то в Formula Bar появится формула
{ =(X-m)/s}, заключенная в фигурные скобки
{}. Это – признак формулы массива. .
Рис.26
Формула массива
Решение матриц в Excel
С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.
Транспонирование
Транспонировать матрицу – поменять строки и столбцы местами.
Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.
- 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
- 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.
Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.
Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.
Сложение
Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.
В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.
Умножение матриц в Excel
Условие задачи:
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).
Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.
В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.
Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.
Обратная матрица в Excel
Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).
Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.
Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:
1 .10. Построение графиков
В Excel можно строить диаграммы разных типов. Но для нас
интересны только два вида: диаграмма рассеяния (scatter) и график (line).
Пример диаграммы рассеяния приведен на Рис. 24 .
Рис.24
Диаграмма рассеяния
Диаграммы такого типа используются для построения графиков
счетов, зависимостей «измерено-предсказано», и т.п. От линейных графиков
они отличаются равноправием обеих осей. В линейных графиках ось абсцисс
предназначена только для отображения категорийных переменных, т.е.
величин, в которых важна не их величина, а порядок следования. Поэтому
линейные графики подходят для представления зависимостей от числа
главных компонент, например, для изображения того, как величины RMSEC и
RMSEP меняются при усложнении модели.
Методы построения графиков в версиях 2003 и 2007 сильно
отличаются. Поэтому мы не будем на этом останавливаться, предоставив эту
тему для
самостоятельного изучения .
характеристики
Свойства группы
Набор регулярных матриц фиксированного размера над унитарным кольцом вместе с умножением матриц в качестве зацепления образует (обычно некоммутативную ) группу , общую линейную группу . В этой группе единичная матрица является нейтральным элементом, а обратная матрица — обратным элементом . Таким образом, ясно определена инверсия матрицы, а также левая и правая инверсия. В частности, обращение к единичной матрице снова приводит к единичной матрице, то есть
Р.{\ displaystyle R} GL(п,Р.){\ Displaystyle \ OperatorName {GL} (п, R)}
- Я.-1знак равноЯ.{\ displaystyle I ^ {- 1} = I},
и инверсия обратной матрицы снова является выходной матрицей, то есть
- (А.-1)-1знак равноА.{\ Displaystyle \ влево (А ^ {- 1} \ вправо) ^ {- 1} = А}.
Поэтому матрицы и также называются обратными друг другу. Произведение двух регулярных матриц снова является правильным, а обратное произведение является произведением соответствующего обратного, но в обратном порядке:
А.{\ displaystyle A}А.-1{\ displaystyle A ^ {- 1}}
- (А.⋅Б.)-1знак равноБ.-1⋅А.-1{\ Displaystyle \ влево (A \ cdot B \ right) ^ {- 1} = B ^ {- 1} \ cdot A ^ {- 1}}.
Если матрицу можно представить как произведение легко обратимых матриц, то таким образом можно быстро определить обратную матрицу. Общая формула произведения применяется к обратному произведению нескольких матриц.
- (А.1⋅А.2⋯А.k)-1знак равноА.k-1⋯А.2-1⋅А.1-1{\ displaystyle \ left (A_ {1} \ cdot A_ {2} \ dotsm A_ {k} \ right) ^ {- 1} = A_ {k} ^ {- 1} \ dotsm A_ {2} ^ {- 1 } \ cdot A_ {1} ^ {- 1}}
с . Это особенно относится к обратной матрице степениk∈N{\ Displaystyle к \ в \ mathbb {N}}
- (А.k)-1знак равно(А.-1)k{\ displaystyle \ left (A ^ {k} \ right) ^ {- 1} = \ left (A ^ {- 1} \ right) ^ {k}}.
Эта матрица также отмечена.
А.-k{\ displaystyle A ^ {- k}}
Прочие свойства
Следующие дополнительные свойства применяются к обратной матрице с записями из тела . Верно
обратное к произведению матрицы на скаляр сK{\ displaystyle K}c∈K{\ displaystyle c \ in K}c≠{\ displaystyle c \ neq 0}
- (cА.)-1знак равноc-1А.-1{\ Displaystyle (СА) ^ {- 1} = с ^ {- 1} А ^ {- 1}}.
Обратная транспонированная матрица равна транспонированной обратной, поэтому
- (А.Т)-1знак равно(А.-1)Т{\ displaystyle \ left (A ^ {T} \ right) ^ {- 1} = \ left (A ^ {- 1} \ right) ^ {T}}.
То же самое относится и к обратной к присоединенной комплексной матрице
- (А.ЧАС)-1знак равно(А.-1)ЧАС{\ displaystyle \ left (A ^ {H} \ right) ^ {- 1} = \ left (A ^ {- 1} \ right) ^ {H}}.
Эти две матрицы также иногда записываются через и . Относится к в ранге обратного
А.-Т{\ displaystyle A ^ {- T}}А.-ЧАС{\ displaystyle A ^ {- H}}
- классифицировать(А.-1)знак равноклассифицировать(А.)знак равноп{\ displaystyle \ operatorname {rank} \ left (A ^ {- 1} \ right) = \ operatorname {rank} (A) = n}
и для его определителя
- Det(А.-1)знак равно(DetА.)-1{\ displaystyle \ operatorname {det} \ left (A ^ {- 1} \ right) = (\ det A) ^ {- 1}}.
Если собственное от того, является к собственному вектору , то собственное число является также собственным вектором .
λ{\ displaystyle \ lambda}А.{\ displaystyle A} Икс{\ displaystyle x}λ-1{\ displaystyle \ lambda ^ {- 1}}А.-1{\ displaystyle A ^ {- 1}}Икс{\ displaystyle x}
Инварианты
Некоторые обычные матрицы сохраняют свои пользовательские свойства при инверсии. Примеры этого:
- верхние и нижние треугольные матрицы, а также строго верхние и нижние треугольные матрицы
- положительно определенные и отрицательно определенные матрицы
- симметричные , персимметричные , бисимметричные и центрально-симметричные матрицы
- унимодулярные и целочисленные унимодулярные матрицы
Функции для работы с матрицами в Excel
В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.
Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.
Формулы массива
Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).
Порядок применения формулы массива:
- Выделить диапазон, где должен появиться результат действия формулы.
- Ввести формулу (как и положено, со знака «=»).
- Нажать сочетание кнопок Ctrl + Shift + Ввод.
В строке формул отобразится формула массива в фигурных скобках.
Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.
Решение матриц в Excel
С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.
Транспонирование
Транспонировать матрицу – поменять строки и столбцы местами.
Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.
- 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
- 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.
Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.
Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.
Сложение
Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.

В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.
Умножение матриц в Excel
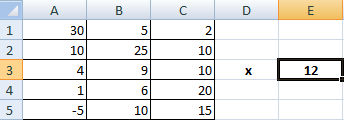
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).
Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.

В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.
Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.
Обратная матрица в Excel
Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).
Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.
Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:
Нахождение определителя матрицы
Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.
Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).
Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.
3 .3 . Пример макроса
Второй способ опирается на рекуррентное соотношение,
связывающее два соседних члена в ряду
Для того чтобы воспользоваться этим соотношением, надо
организовать на листе рекуррентную процедуру. Например, так, как
показано на Рис. 42
Рис.42
Вычисление функции E
1 (x
)
итерационным способом
Один шаг итерации – это переход от значений в области
J2:J4
к значениям в области
L2:L4
. Для того, чтобы сделать следующую
итерацию, нужно скопировать значения, получившиеся в области
L2:L4
и вставить их в область
J2:J4
. При этом вставлять нужно только
величины, без формул. Величины в области H2:H4
дают исходные значения для начала итерации.Повторяя многократно
операцию Copy-Paste Special
, можно получить в
ячейке L4
искомое значение. Однако
копирование – это скучное занятие и его было бы неплохо
автоматизировать. Для этого можно написать макрос.
Проще всего начать создание макроса через запись команд,
выполняемых на листе. Для этого идем в раздел меню Tools–Macro–Record
New Macro
. Появляется окно (Рис. 43
), в котором можно указать имя
макроса и где он будет расположен.
Рис.43
Запись макро
После нажатия OK
начинается
запись всех действий, выполняемых на листе. Когда все, что нужно
сохранено в макросе, запись надо остановить командой
Tools–Macro–Stop Recording
. Результат можно увидеть, зайдя в
редактор Visual Basic
.
Рис.44
Редактор Visual Basic
На Рис.
Рис.45
Функция IntExp
На Рис. 45
приведен
код этой функции и пример обращения к
ней.
Мы не будем рассказывать о программировании на VBA, т.к.
это очень большой и сложный вопрос. Самостоятельно его можно изучить по
имеющимся в сети многочисленным пособиям, например,
.
VBA – это довольно медленный язык и он плохо подходит
для больших вычислений. Например, не стоит писать на этом языке
процедуру для PCA декомпозиции – на больших массивах она будет считать
очень долго. Правильнее рассматривать Excel и VBA как интерфейс (front
end) для ввода и вывода данных, которые затем передаются в динамическую
библиотеку (DLL), написанную на быстром языке, таком как C++ (back end).
Именно эта концепция и была реализована в надстройках
Fitter
и
Chemometrics
.
Подробнее об использовании пользовательских функций для
расширения возможностей надстройки Chemometrics
можно прочитать
.
Использование математических функций в программе
В категорию математических функций входит более 60 различных операторов, которые позволяют выполнять различные вычисления.
Вставить функцию в свободную ячейку таблицы можно по-разному:
- Жмем кнопку “Вставить функцию” (fx) слева от строки формул. Выполнить данное действие можно, находясь в любой вкладке.
- Переключаемся во вкладку “Формулы”. Здесь также представлена кнопка “Вставить функцию” – в левом углу ленты инструментов.
- Нажимаем комбинацию клавиш Shift+F3, чтобы вызвать Мастер функций.
Результатом любого из вышеописанных способов будет открытие окна вставки функции. Здесь мы выбираем категорию “Математические”.
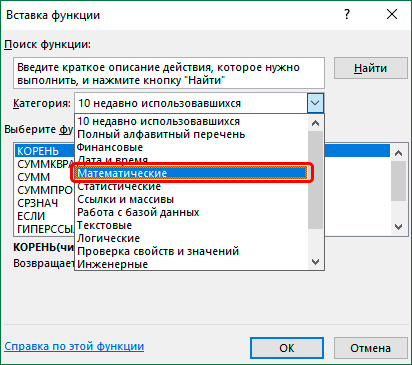
Теперь, когда категория выбрана, в поле ниже отмечаем требуемую функцию и щелкаем OK.
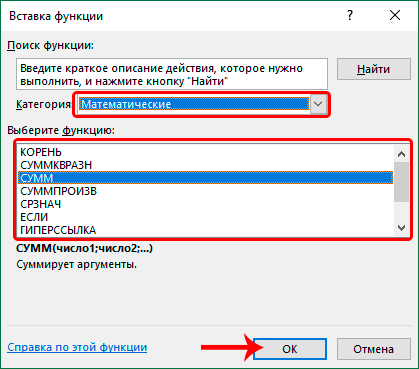
После этого откроется окно с аргументами для заполнения.
Примечание: Если мы, находясь во вкладке “Формулы”, в группе инструментов “Библиотека функций” нажмем по значку математических функций, сразу откроется список операторов, которые мы можем выбрать, минуя окно вставки функции.
Стоит учитывать, что в предлагаемом перечне присутствуют не все операторы, но самые необходимые здесь все же есть, и в большинстве случаев их достаточно.
Теперь перейдем к детальному рассмотрению самых популярных функций.
Пожалуй, это самая популярная функция, которая используется в Эксель. С помощью нее выполняется суммирование числовых данных. Формула функции:
В аргументах можно указать как конкретные числа, так и ссылки на ячейки, содержащие числовые значения. Причем указать координаты можно вручную (с помощью клавиш клавиатуры) или методом клика/выделения непосредственно в самой таблице.
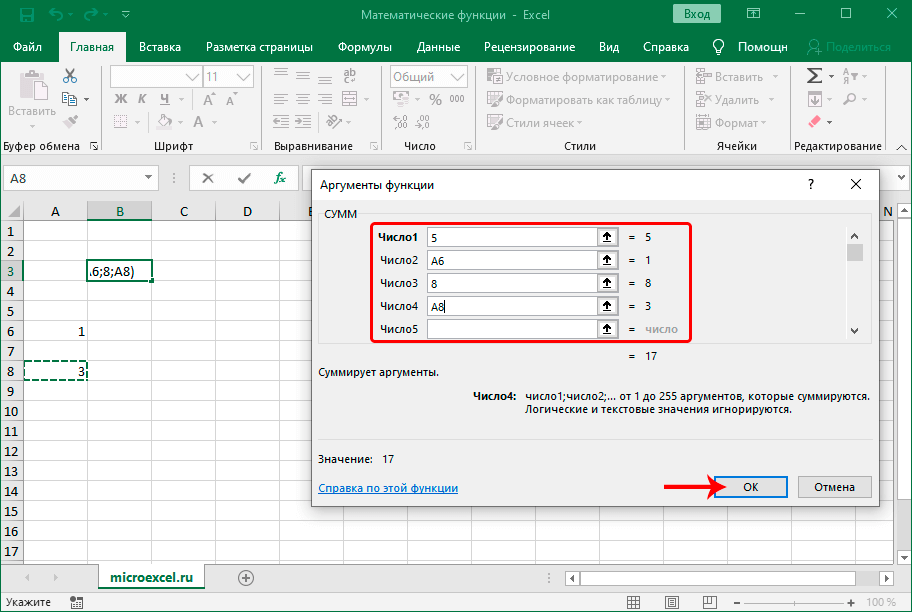
Для перехода к заполнению следующего аргумента достаточно кликнуть по полю напротив него или нажать клавишу Tab.
СУММЕСЛИ
Данная функция позволяет считать сумму чисел с заданным условиями, с помощью которых будет выполняться отбор значений, учитывающихся в суммировании. Формула выглядит следующим образом:
В аргументах функции указывается диапазон ячеек (вручную или путем выделения в таблице), значения которых нужно просуммировать. В качестве критерия можно задать следующие условия (в кавычках):
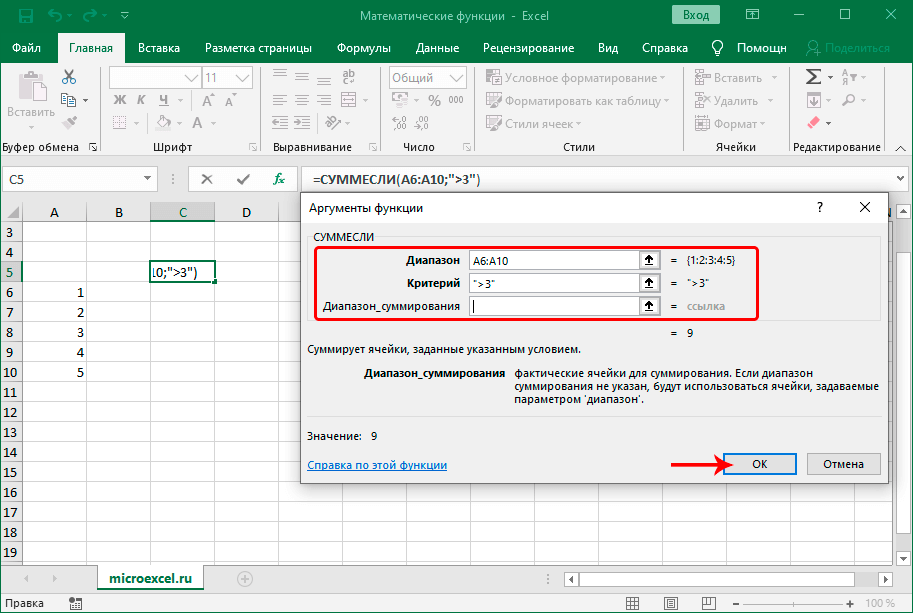
Аргумент “Диапазон_сумирования” заполнять не обязательно.
ПРОИЗВЕД
С помощью данного оператора выполняется умножение чисел. Синтаксис выглядит следующим образом:
В аргументах функции, как и в СУММ, можно указывать как конкретные числа, так и адреса ячеек (диапазоны ячеек), которые содержат числовые значения.
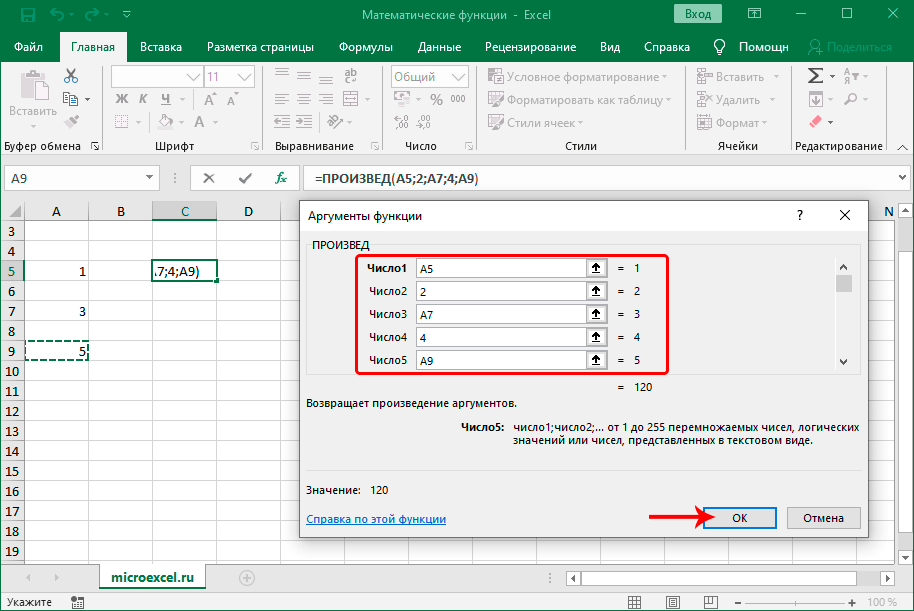
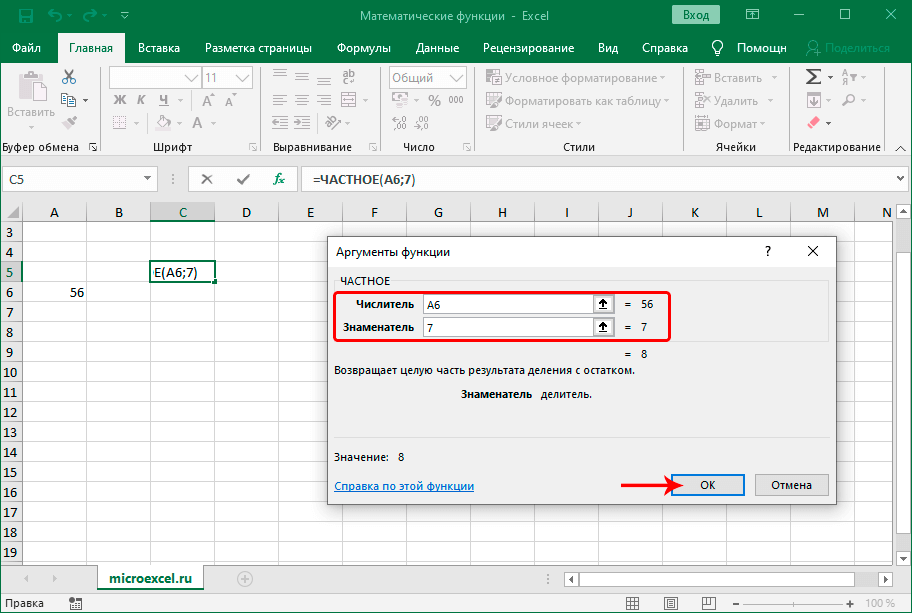
ЧАСТНОЕ
Чаще всего для деления используется формула со знаком “/” между делимым и делителем: =Число1/Число2 .
Однако в программе также есть отдельная функция для выполнения деления, синтаксис которой представлен ниже:
Заполнить нужно два аргумента: Числитель (Делимое) и Знаменатель (Делитель).
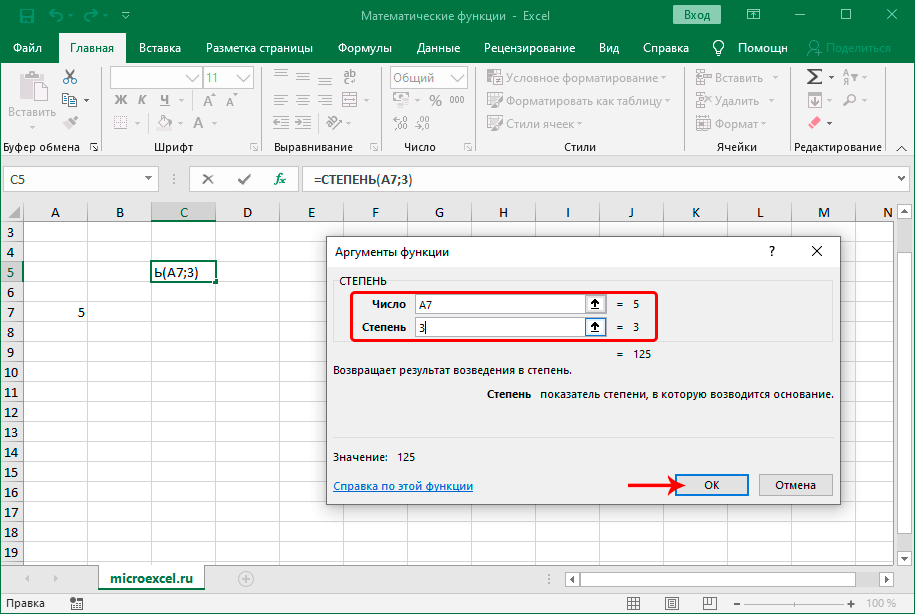
СТЕПЕНЬ
Оператор позволяет возвести число в указанную степень. Формула выглядит так:
В аргументах функции указывается само число, а также, степень, в которую нужно его возвести.
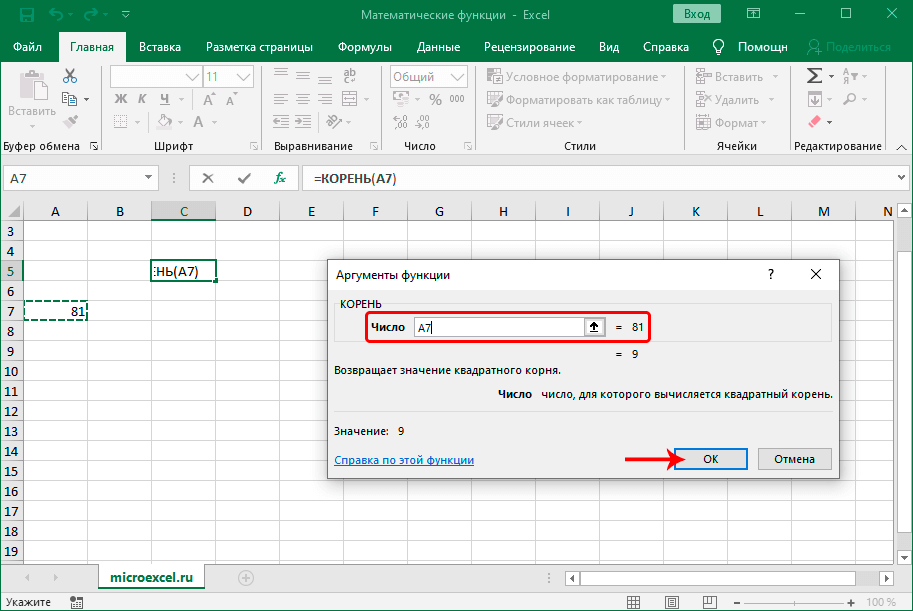
КОРЕНЬ
С помощью данного оператора можно извлечь квадратный корень из числа. Синтаксис выглядит следующим образом:
Заполнить требуется только один аргумент – “Число”.
ОКРУГЛ
Функция применяется для выполнения еще одного распространенного математического действия – округления чисел (по общематематическим правилам, т.е., к ближайшему по модулю значению). Синтаксис функции представлен ниже:
В аргументе “Число” указывается значение, которое требуется округлить. В числе разрядов, соответственно, пишем количество цифр, которые хотим оставить после запятой.
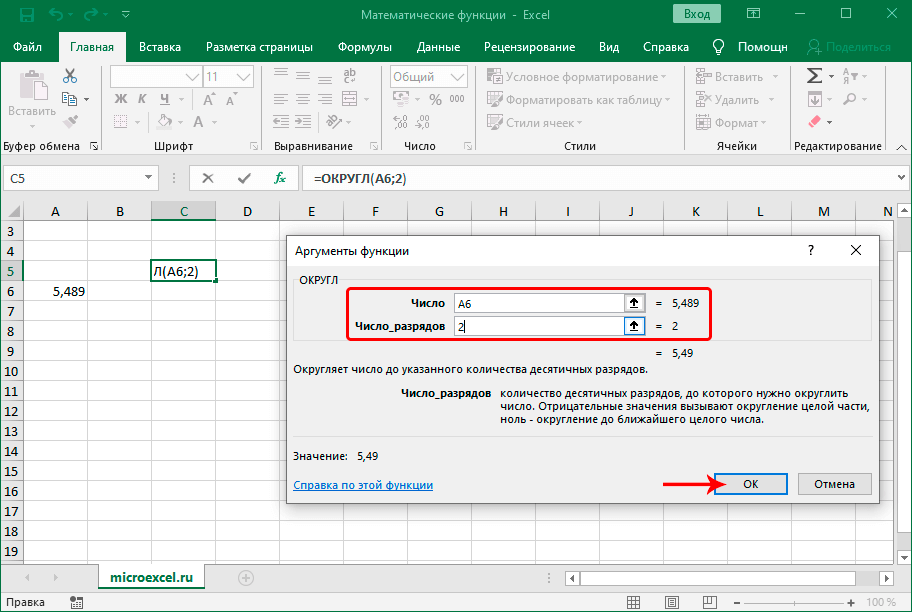
Также, в Excel доступны операторы ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые, как следует из их названий, используются для округления до ближайшего верхнего и нижнего числа, соответственно (по модулю).
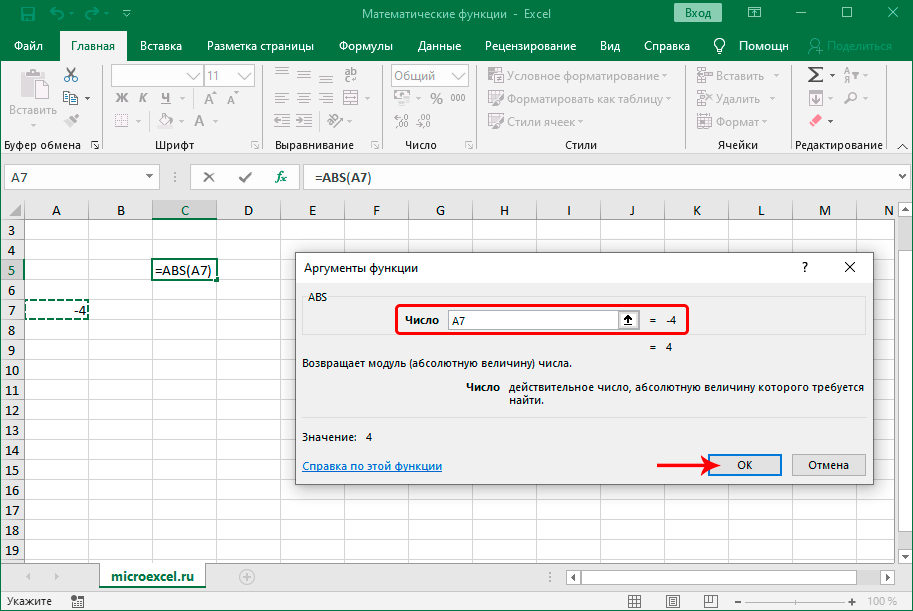
Позволяет получить модуль числа. Формула функции представлена ниже:
Заполнить нужно всего один аргумент – “Число”, модуль которого требуется найти.
С помощью этого оператора определяется логарифм числа по заданному основанию. Синтаксис функции представлен в виде:
Необходимо заполнить два аргумента: Число и Основание логарифма (если его не указать, программа примет значение по умолчанию, равное 10).
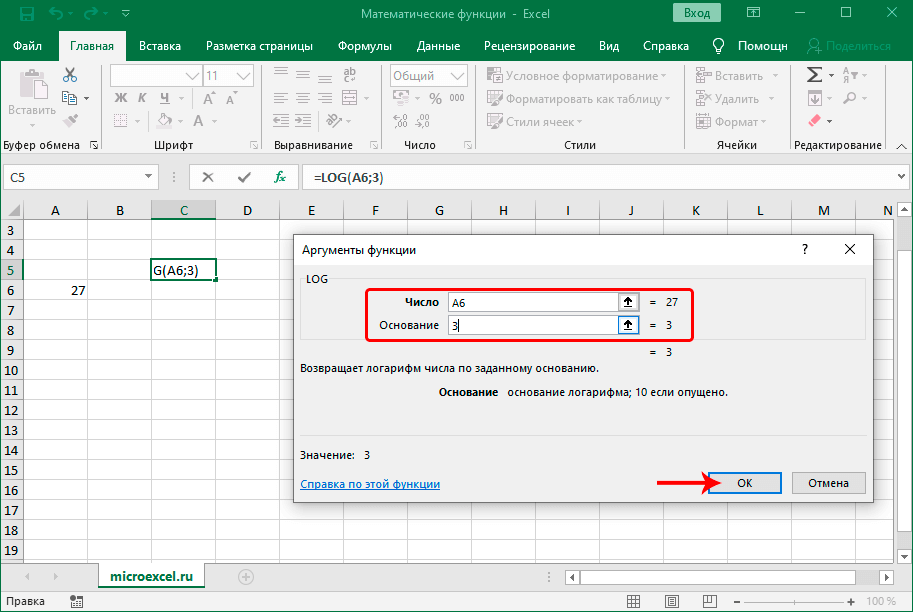
Также для десятичного логарифма предусмотрена отдельная функция – LOG10.
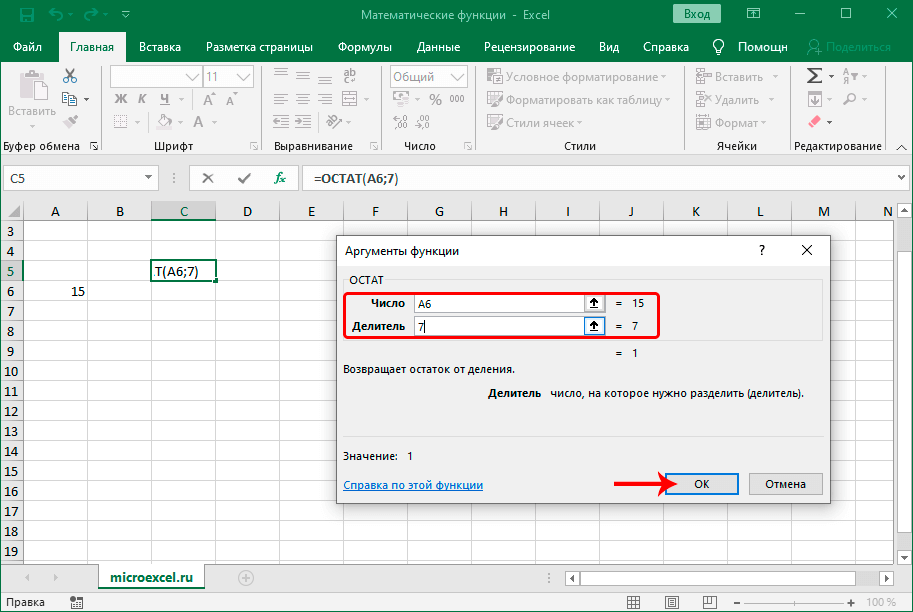
ОСТАТОК
Применяется для получения остатка от деления чисел. Формула оператора выглядит следующим образом:
Для того, чтобы получить результат, требуется заполнить значения двух аргументов: Число и Делитель.