Второй способ нахождения процента
Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.
Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.
Запись 50% заменяет собой запись , а если перевести эти в десятичную дробь, то мы получим 0,5
Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5
300 × 0,5 = 150
Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %

6. Формула расчета простых процентов. Расчет процентов на банковский вклад
Если проценты на депозит начисляются один раз в конце срока вклада, то расчет процентов выполняется по формуле простых процентов:
Sp = K * P/100 * d/D
Формула расчета вклада с процентами:
S = K + K * P/100 * d/D
Иногда удобнее использовать формулу расчета в таком виде:
S = K * (1 + P/100 * d/D)
Где:
S — сумма банковского вклада с процентами,
Sp — сумма процентов (доход),
K — первоначальный вклад (капитал),
P — годовая процентная ставка,
d — количество дней начисления процентов по привлеченному вкладу,
D — количество дней в календарном году (365 или 366).
Пример 6.1 Банком принят вклад 100 тыс. рублей сроком на 1 год по ставке 20%.
S = 100000 + 100000 * 20/100 * 365/365 = 120000
Sp = 100000 * 20/100 * 365/365 = 20000
Пример 6.2 Банком принят вклад 100 тыс. рублей сроком на 30 дней по ставке 20% годовых.
S = 100000 + 100000 * 20/100 * 30/365 = 101643.84
Sp = 100000 * 20/100 * 30/365 = 1643.84
Онлайн калькулятор
Расчет вклада с процентами
Как найти процент от числа пример
Вычисление процента от суммы – это важный навык, который помогает понимать расходы и доходы в нашей жизни. Рассмотрим пример, как найти процент от числа:
- Шаг 1: Разделите процент на 100, чтобы получить долю от суммы.
- Шаг 2: Умножьте исходное число на долю процента.
Например, если вам нужно найти 15% от суммы 300 рублей:
- Доля процента: 15 / 100 = 0,15
- Умножение на долю процента: 300 рублей x 0,15 = 45 рублей
Таким образом, 15% от 300 рублей составляет 45 рублей.
Также можно использовать таблицу процентов для быстрого вычисления процента от числа. Например, если процент равен 20%, то вы можете найти долю процента в таблице и умножить на исходную сумму.
| Процент | Доля |
|---|---|
| 10% | 0,1 |
| 20% | 0,2 |
| 30% | 0,3 |
| 40% | 0,4 |
| 50% | 0,5 |
Таким образом, для нахождения 20% от суммы 500 рублей необходимо умножить 500 рублей на 0,2, что равно 100 рублям.
Каким образом перевести процент в десятичную дробь?
Перевод процента в десятичную дробь может понадобиться при работе с различными вычислениями и формулами. Для этого необходимо выполнить небольшое преобразование, которое позволит перевести процент в числовое значение.
Чтобы перевести процент в десятичную дробь, нужно разделить значение процента на 100. Например, если имеется процентное значение 75%, чтобы перевести его в десятичную дробь, нужно выполнить следующую операцию: 75/100 = 0.75.
Таким образом, проценты могут быть представлены в виде десятичных дробей, где значение от 0 до 1 соответствует диапазону от 0% до 100%. Например, значения процентов 50% и 75% переводятся соответственно в десятичные дроби 0.5 и 0.75.
Удобство перевода процента в десятичную дробь заключается в том, что десятичные дроби легче использовать для математических расчетов, чем проценты. Например, при умножении числа на процент, необходимо будет сначала перевести процент в десятичную дробь, а затем выполнить вычисление. Поэтому перевод процента в десятичную дробь является важным навыком при работе с числовыми значениями.
Проценты: правила
Рассмотрим четыре известных способа поиска процентов.
|
Занимайтесь математикой в удовольствие вместе с нашими преподавателями на онлайн-курсах по математике для детей и подростков! |
Нахождение одного процента от числа
Найти процент от числа можно несколькими способами.
Первый способ
-
Найдем, чему равен 1%.
-
Умножим полученное значение на количество искомых процентов.
Пример: найти 12% от числа 48.
-
48 : 100 = 0,48.
-
0,48 × 12 = 5,76.
Второй способ
-
Переведем проценты в десятичную дробь.
-
Умножим число на полученную десятичную дробь.
Давайте снова найдем 12% от 48, но другим способом.
-
12 : 100 = 0,12.
-
48 × 0,12 = 5,76.
Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?
|
Как решаем:
|
Ответ: выгоднее воспользоваться скидкой 15%.
Составление пропорции
Равенство двух отношений называют пропорцией.
a : b = c : d или a/b = c/d
- a, d — крайние члены
- b, c — средние члены
Читается: а относится к b так, как с относится к d
Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение
Рассмотрим пример. Насколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?
|
Как решаем: Найдем, сколько рублей составляет выгода, то есть скидка в 14%. Обозначим стоимость футболки за 100%, значит 1390 рублей = 100%. Тогда 14% это х рублей. Получаем пропорцию: 1390 руб. = 100% x руб. = 14% Перемножим крест-накрест и найдем x: x = 1390 × 14 : 100 x = 194,6 |
Ответ: выгода по скидке составила 194,6 рубля.
Соотношения чисел
Есть случаи, при которых можно использовать простые дроби. Например, 10% — это десятая часть целого. Чтобы найти 10% от числа a, нужно разделить его на 10. Собрали примеры соотношения чисел в таблице.
| Процент | Дробь | Как найти % от числа a |
|---|---|---|
| 10% | 1/10 | a : 10 |
| 20% | 1/5 | a : 5 |
| 25% | 1/4 | a : 4 |
| 50% | 1/2 | a : 2 |
| 75% | 3/4 | a : 4 × 3 |
Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?
|
Как решаем:
|
Ответ: средств хватит, так как пиджак стоит 6375 рублей.
Как узнать на сколько процентов одно число
Для того чтобы определить, насколько процентов одно число превышает другое, необходимо разделить первое число на второе, затем умножить результат на 100 и вычесть из него 100. Формула для вычисления этого процента выглядит так: Р = Ч1/Ч2 х 100 — 100. Например, если нужно узнать, на сколько процентов число 20 больше числа 5, то необходимо выполнить следующие действия: 20/5 х 100 — 100 = 300%. Это означает, что число 20 в три раза больше числа 5. На основе этой формулы можно вычислить разницу в доходах двух сотрудников: если начальник зарабатывает 50000 рублей, а сотрудник — 35000, то разница между их доходами составляет примерно 42,9% (50000/35000 х 100 — 100 ≈ 42,9%).
Как правильно рассчитать проценты от суммы
Рассчитывать проценты от суммы — это важный навык, который пригодится в жизни каждого из нас. Чтобы правильно посчитать проценты, необходимо знать несколько простых правил.
- Шаг 1. Определите процент, который необходимо рассчитать. Например, если вы хотите рассчитать 10% от 1000 рублей, то процент составляет 10.
- Шаг 2. Определите сумму, от которой вы хотите рассчитать процент. Так, в нашем примере сумма равна 1000 рублей.
- Шаг 3. Переведите процент в дробь. Для этого необходимо разделить процент на 100. В нашем примере 10% равно 0,1.
- Шаг 4. Умножьте сумму на дробь-процент. То есть, умножьте 1000 рублей на 0,1. Получите результат — 100 рублей.
- Шаг 5. Итоговое число — это и есть сумма, равная проценту от начальной суммы. Так, в нашем примере, 10% от 1000 рублей составляет 100 рублей.
Как видите, рассчитать проценты от суммы несложно, если знать правила. Изучите эти шаги и применяйте их в жизни, чтобы правильно вычислять проценты от начальной суммы.
Процентный калькулятор: 7 основных операций с процентами
Один процент — это сотая часть от числа. Данное понятие используется, когда нужно обозначить отношение доли к целому.
Кроме этого, в процентах можно сравнивать несколько величин, при этом обязательно указывая, относительного какого целого проценты вычисляются.
Например, расходы выше доходов на 10 % или цена на железнодорожные билеты возросла на 15 % в сравнении с тарифами прошлого года. Число процентов выше 100 означает, что доля превышает целое, как часто бывает при статистических расчетах.
Процент как финансовое понятие — плата, заемщика кредитору за предоставление денег во временное пользование. В бизнесе встречается выражение «работать за проценты».
В данном случае подразумевается, что размер вознаграждения зависит от прибыли или оборота (комиссионные). Обойтись без вычисления процентов невозможно в бухгалтерии, бизнесе, банковском деле.
Чтобы упростить расчеты, разработан онлайн-калькулятор процентов.
Калькулятор позволяет вычислить:
- Процент от заданного значения.
- Процент из суммы (налог по фактической зарплате).
- Процент от разницы (НДС из суммы с НДС).
При решении задач на калькуляторе процентов нужно оперировать тремя значениями, одно из которых неизвестно (по заданным параметрам вычисляется переменная). Сценарий расчета следует выбирать, исходя из заданных условий.
1. Вычисление процента от числа
Чтобы найти число, составляющее 25 % от 1 000 руб., нужно:
- 1 000 × 25 / 100 = 250 руб.
- Или 1 000 × 0,25 = 250 руб.
Для расчета на обычном калькуляторе, нужно 1 000 умножить на 25 и нажать кнопку %.
2. Определение целого числа (100 %)
Мы знаем, что 250 руб. составляет 25 % от какого-то числа. Как его вычислить?
Составим простую пропорцию:
- 250 руб. — 25 %
- Y руб. — 100 %
- Y = 250 × 100 / 25 = 1 000 руб.
3. Процент между двумя числами
Допустим, предполагалась прибыль 800 руб., а получили 1 040 руб. Каков процент превышения?
Пропорция будет такой:
- 800 руб. — 100 %
- 1 040 руб. – Y %
- Y = 1 040 × 100 / 800 = 130 %
Перевыполнения плана по прибыли — 30 %, то есть выполнение — 130 %.
4. Расчет не из 100 %
Например, в магазин, состоящий из трех отделов, приходят 100 % покупателей. В продуктовый отдел — 800 человек (67 %), в отдел бытовой химии — 55. Какой процент покупателей приходит в отдел бытовой химии?
Пропорция:
- 800 посетителей – 67 %
- 55 посетителей — Y %
- Y = 55 × 67 / 800 = 4,6 %
5. На сколько процентов одно число меньше другого
Цена товара упала с 2 000 до 1 200 руб. На сколько процентов подешевел товар или на сколько процентов 1 200 меньше 2 000?
- 2 000 — 100 %
- 1 200 – Y %
- Y = 1 200 × 100 / 2 000 = 60 % (60 % к цифре 1 200 от 2 000)
- 100 % − 60 % = 40 % (число 1 200 меньше 2 000 на 40 %)
6. На сколько процентов одно число больше другого
Зарплата выросла с 5 000 до 7 500 рублей. На сколько процентов увеличилась зарплата? На сколько процентов 7 500 больше 5 000?
- 5 000 руб. — 100 %
- 7 500 руб. — Y %
- Y = 7 500 × 100 / 5 000 = 150 % (в цифре 7 500 150 % от 5 000)
- 150 % − 100 % = 50 % (число 7 500 больше 5 000 на 50 %)
7. Увеличение числа на определенный процент
Цена товара S выше 1 000 руб. на 27 %. Какова цена товара?
- 1 000 руб. – 100 %
- S — 100 % + 27 %
- S = 1 000 × (100 + 27) / 100 = 1 270 руб.
Онлайн-калькулятор делает вычисления намного проще: вам нужно выбрать вид расчета, ввести число и процент (в случае вычисления процентного соотношения — второе число), указать точность расчета и дать команду о начале действий.
Процент как сотая часть
$$1\% = 0.01$$
Мы привыкли, что сотая часть метра – это сантиметр. С помощью процентов мы можем обозначить сотую часть чего угодно – например, населения страны, заработанных денег, объёма кастрюли…
При сравнении двух величин за $100\%$ чаще всего принимается та величина, которая больше. Например, если мы говорим «$5\%$ учащихся школы», значит, $100\%$ — это все учащиеся школы.
Иногда за $100\% $ принимают исходную величину. Например, если говорится, что прибыль от фильма составила $134\%$, значит, расходы на фильм полностью окупились (на $100\%$), и плюс он принёс доход в размере $34\%$ от потраченных на съёмки денег.
{"questions":[{"content":"Детское фруктовое пюре на $49\\%$ состоит из яблок, на $35\\%$ из груш, на $12\\%$ из персиков. Также в состав входят вода и лимонный сок. Сколько процентов приходится на эти добавки?`input-1`","widgets":{"input-1":{"type":"input","answer":"4"}},"step":1,"hints":["Сначала найдём, сколько процентов составляют все фрукты вместе, для этого сложим число процентов. <br />$49 + 35 + 12 = 96 \\%$","За $100 \\%$ принимаем весь состав пюре. Значит, чтобы найти процентное число добавок, нам нужно из $100$ вычесть процент фруктов. У нас получится $4$."]}]}
Нахождения числа по его проценту
Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.
Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:
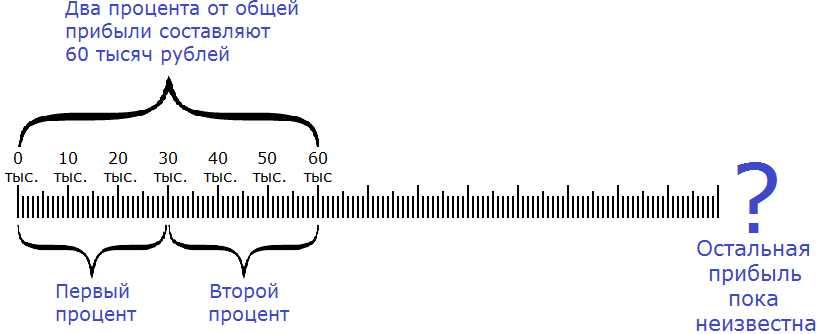
Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2
60 000 : 2 = 30 000
Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100
30 000 × 100 = 3 000 000
Мы нашли общую прибыль. Она составляет три миллиона.
Попробуем сформировать правило нахождения числа по его проценту.
Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.
Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.
Читаем первую часть правила:
Чтобы найти число по его проценту, нужно известное число разделить на данный процент
У нас известное число это 35, а данный процент это 7. Разделим 35 на 7
35 : 7 = 5
Читаем вторую часть правила:
и полученный результат умножить на 100
У нас полученный результат это число 5. Умножим 5 на 100
5 × 100 = 500
500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35
500 : 100 = 5
5 × 7 = 35
Получили 35. Значит задача была решена правильно.
Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.
Например, предыдущая задача может быть изложена так: число 35 это от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100
35 : 7 = 5
5 × 100 = 500
В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.
Примеры перевода процента в число
Для перевода процента в число необходимо выполнить простое математическое действие. Например, если нужно перевести 25% в число, то можно использовать следующую формулу:
число = процент / 100
Таким образом, для перевода 25% в число, необходимо поделить 25 на 100. Получается:
число = 25 / 100 = 0.25
Еще одним примером перевода процента в число может служить ситуация, когда нужно вычислить 50% от определенного значения. Для этого также применяется формула:
число = (процент / 100) * значение
Так, если мы хотим найти 50% от значения 200, то сначала находим 50 / 100 = 0.5, а затем умножаем на исходное значение:
число = 0.5 * 200 = 100
Кроме того, перевод процента в число может применяться при рассчете скидок. Например, если товар имеет скидку 20%, то для определения конечной цены нужно применить формулу:
число = значение — (процент / 100) * значение
Подставив значения в формулу, получим:
число = 100 — (20/100) * 100 = 80
Таким образом, перевод процента в число позволяет удобно проводить различные математические операции с процентами и получать конкретные числовые значения.
Полезные советы
Вот несколько советов, которые могут помочь при расчете процентов:
- Освойте основные формулы для расчета процентов, такие как формулы для нахождения процентного соотношения, процентного приращения или процентного уменьшения.
- Помните, что проценты могут быть выражены как десятичные дроби, например, 50% может быть записано как 0.5.
- Не забывайте учитывать порядок операций, например, в выражении «25% от 80» сначала нужно умножить 80 на 0,25, а затем округлить результат.
- Используйте дроби для более точных расчетов, особенно если нужно произвести несколько операций. Например, вы можете записать «25% от 80» как 1/4 от 80.
- Учитывайте различные типы процентов, например, простые и сложные проценты. Для расчета сложных процентов вам может потребоваться использовать формулу с учетом периода начисления процентов.
- Используйте калькулятор при необходимости, особенно при более сложных расчетах. Это может помочь избежать ошибок при пересчете значений.
- Не забывайте проверять свои расчеты на ошибки и перепроверять полученные результаты, чтобы убедиться в их правильности.
Вопросы и ответы
А вот несколько ответов на часто задаваемые вопросы при вычислении процентов.
Как вычислить процент от числа?
Для вычисления процента от числа нужно умножить число на процентное соотношение (долю) в виде десятичной дроби. Например, чтобы найти 25% от числа 200, нужно выполнить следующее вычисление: 200 x 0,25 = 50.
Как вычислить число, которому соответствует определенный процент?
Чтобы найти число, соответствующее определенному проценту, нужно разделить процентное значение на процентное соотношение (долю) в виде десятичной дроби. Например, чтобы найти число, которому соответствует 20%, нужно выполнить следующее вычисление: 20 ÷ 100 x N = N x 0,2.
Как вычислить процент изменения?
Чтобы вычислить процент изменения, нужно найти разницу между начальным и конечным значениями, разделить ее на начальное значение и умножить на 100%. Например, если начальное значение равно 100, а конечное значение равно 120, то процент изменения будет: ((120-100) ÷ 100) x 100% = 20%.
Как вычислить начальное значение при известном конечном значении и процентном изменении?
Чтобы найти начальное значение при известном конечном значении и процентном изменении, нужно разделить конечное значение на 1 плюс процент изменения в виде десятичной дроби. Например, если конечное значение равно 120, а процент изменения равен 20%, то начальное значение будет: 120 ÷ (1 + 0,2) = 100.
Как вычислить конечное значение при известном начальном значении и процентном изменении?
Чтобы найти конечное значение при известном начальном значении и процентном изменении, нужно умножить начальное значение на 1 плюс процент изменения в виде десятичной дроби. Например, если начальное значение равно 100, а процент изменения равен 20%, то конечное значение будет: 100 x (1 + 0,2) = 120.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор процентов от числа. Рассчитайте онлайн значение процента от любого числа с помощью данного калькулятора.
- Калькулятор процентов. Рассчитайте онлайн процент от числа, на сколько процентов одно число больше или меньше другого, или сколько процентов составляет одно число от другого числа, а также прибавьте или вычтете процент к числу.
- Добавить процент к числу. Прибавьте онлайн любой процент к любому числу с помощью специального калькулятора.
- На сколько процентов больше. Рассчитайте онлайн, на сколько процентов одно число больше другого.
- На сколько процентов меньше. Рассчитайте онлайн, на сколько процентов одно число меньше другого.
- Инженерный калькулятор. Посчитайте сложные примеры на продвинутом калькуляторе.
- Калькулятор сложного процента. Рассчитайте на инвесткалькуляторе сумму, полученную в результате применения сложного процента с реинвестированием, регулярным пополнением, капитализацией и с примерами.
- Бросить монетку онлайн. С помощью данной формы вы можете подбросить монетку онлайн любое количество раз.
- Калькулятор НДФЛ. Рассчитайте онлайн НДФЛ от суммы на руки или полной зарплаты по разным ставкам.
- Сумма прописью. Переведите сумму в виде цифр в сумму прописью — текстом. Сделайте расшифровку правильно для договоров и других документов.
Примеры решения задач на проценты
1. Расчет процента от числа
Найти число M, которое составляет P% от числа N.
В этом уравнении и в уравнениях ниже:
P% — процент, то есть число или отношение, выраженное в форме сотой части. В нашем примере P = 25%.
N — первое число (исходное число) , в нашем примере N = 150.
M — второе число, в нашем примере M = 37.5.
Пример: Сколько будет 25% от 150?
Результат: 25% от 150 равно 37.5.
2. Расчет процента увеличения или уменьшения, если известны исходное и новое значение
Какой процент P от N составляет число M? Иными словами, найти неизвестное число P, если известно, что P% от N равно M.
Пример: Какой процент от 200 составляет число 25?
Результат: 25 — это 12% от 200.
3. Расчет исходного числа по известному проценту от этого числа
Определить исходное число, если известно, что P% от этого числа равны M.
Пример: Определить исходное число, если известно, что 200% от этого числа равны 50. Иными словами, 50 — это 200% от какого числа?
Результат: 200% от 25 равны 50.

4. Расчет процентного увеличения (разницы в процентах между двумя числами)
Определить процент (P) увеличения исходного значения N, если известно, что после увеличения оно равно N.
Пример: На сколько процентов 200 больше 180?
Результат: 200 на 11,11% больше 180.
5. Расчет процентного уменьшения (разницы в процентах между двумя числами)
Определить процент (P) уменьшения исходного значения N, если известно, что после уменьшения оно равно N.
Другой пример: Магазин продавал товары по 20 евро за единицу. Продажа была не слишком успешной, поэтому для стимулирования продаж решили снизить стоимость до 15 евро. Определите убытки на единицу товара в процентном отношении к исходной цене.
Результат: Убытки на каждой единице товара с первоначальной стоимостью 20 евро и новой стоимостью 15 евро составили 25%.
6. Процентное увеличение числа
Определить число M, которое представляет собой P-процентное увеличение числа N.
Пример: Чему равно 10-процентное увеличение числа 5?
Результат: 10-процентное увеличение числа 5 равно 5,5.
7. Процентное уменьшение числа
Определить число M, которое представляет собой P-процентное уменьшение числа N.
Пример: Чему равно 10-процентное уменьшение числа 8?
Результат: 10-процентное уменьшение числа 8 равно 7,2.
Возможно, вас также заинтересует наш Калькулятор выделения и начисления НДС и налога с продаж.
Автор статьи: Анатолий Золотков
Терминологический словарь банковских и финансовых терминов
Плата, взимаемая за заем суммы денег. Процентная ставка есть плата, выраженная как процент от общей кредитуемой суммы, на определенный период времени, обычно на год. Так, процентная ставка, равная 15% ежегодно означает, что за каждые взятые в долг на один год 100 тыс. руб. заемщик должен заплатить 15 тыс. руб. или соответственно больше или меньше в зависимости от периода времени. При простом проценте оплата за кредит рассчитывается только с учетом суммы взятых взаймы денег; таким образом, I = Prt, где I — сумма денег, которую необходимо выплатить в качестве процентов по кредиту, P — основная сумма, r — процентная ставка, t — период времени. При сложном проценте оплата рассчитывается с кредитуемой суммы плюс любой процент, который нарос на нее за предшествующие периоды. В этом случае I = P((1 + r)n — 1), где n — число периодов, для которых процент рассчитывается отдельно. Так, если сумма в 500 тыс. руб. дана взаймы на два года по 12% годовых при поквартальном расчете сложного процента, показатель n составит 4 х 2 = 8, а показатель r — 12:4=3%. Отсюда получаем, что I = 500((1,03)8 — 1) = 133,38 тыс. руб., в то время как при условии простого процента оплата составила бы только 120 тыс. руб. Подобным же образом рассчитываются и проценты на депозиты, где процент является формой дохода. В целом процентные ставки зависят от количества денег в обращении, спроса на заемные средства, политики правительства, оценки кредитором риска невозвращения займа, периода займа и курса валюты относительно других валют.
Второй способ нахождения процента
Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.
Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.
Запись 50% заменяет собой запись , а если перевести эти в десятичную дробь, то мы получим 0,5
Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5
300 × 0,5 = 150
Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %
Проверка обычной дроби на возможность перевода ее в десятичную
Прежде, чем что-либо считать, необходимо убедиться, что полученная в итоге десятичная дробь будет конечной, иначе она окажется бесконечной и высчитать окончательный вариант будет попросту невозможно. Причем бесконечные дроби также могут быть периодическими и простыми, но это уже тема для отдельного раздела.
Перевести обыкновенную дробь в ее конечный, десятичный вариант можно только в том случае, если ее уникальный знаменатель способен раскладываться только на множители 5 и 2 (простые множители). Причем даже в том случае, если они повторяются произвольное количество раз.
Уточним, что оба эти числа являются простыми, так в итоге разделить без остатка их можно только на самих себя, или же, на единицу. Таблицу простых чисел можно отыскать без проблем в сети интернет, это вовсе не сложно, хотя непосредственного отношения к нашему счету она и не имеет.

Рассмотрим примеры:
Дробь 7/40 поддается преобразованию из обычной дроби в ее десятичный эквивалент, потому что ее знаменатель можно без труда разложить на множители 2 и 5.

Однако, если первый вариант даст в результате конечную десятичную дробь, то, к примеру, 7/60 уже никак не даст подобного результата, так как ее знаменатель не будет уже раскладываться на искомые нами числа, а будет иметь в числе множителей знаменателя тройку.
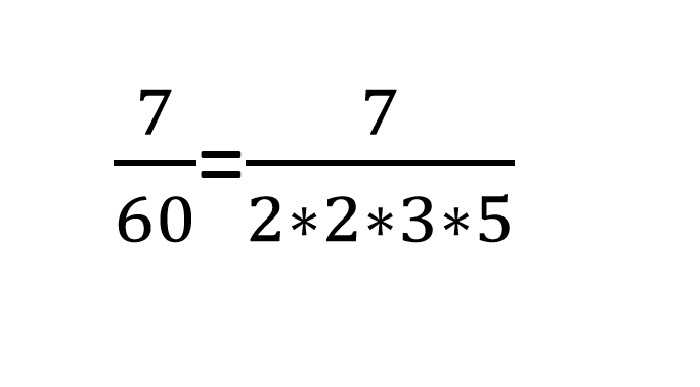
Избавляемся от запятой еще проще
Первый способ детально описывает алгоритм «удаления» запятой из десятичной дроби, однако мы можем упростить этот процесс. И вновь мы выполняем три шага.
Шаг 1
: Считаем, сколько цифр стоит после запятой. К примеру, у числа 1,375 таких цифр три, а у 0,000625 — шесть. Это количество мы обозначим буквой n.
Шаг 2
: Теперь нам достаточно представить дробь в виде C/10 n , где C – это значимые цифры дроби (без нулей, если они есть), а n – количество цифр после запятой. К примеру:
- для числа 1,375 C = 1375, n = 3, итоговая дробь согласно формуле 1375/10 3 = 1375/1000;
- для числа 0,000625 C = 625, n = 6, итоговая дробь согласно формуле 625/10 6 = 625/1000000.
По сути, 10 n – это 1 с количеством нулей, равным n, поэтому вам не нужно заморачиваться с возведением десятки в степень — достаточно указать 1 с n нулей. После этого столь богатую на нули дробь желательно сократить.
Шаг 3
: Сокращаем нули и получаем итоговый результат:
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8;
- 625/1000000 = 1 × 625/ 1600 × 625 = 1/1600.
Дробь 11/8 — это неправильная дробь, так как числитель у нее больше знаменателя, а значит, мы можем выделить целую часть. В этой ситуации мы вычитаем из 11/8 целую часть 8/8 и получаем остаток 3/8, следовательно, дробь выглядит как 1 и 3/8.
Совет 1: Как перевести процент в число
Процент — это по определению сотая часть числа. Поэтому 100% — это фактически единица, то есть само исходное число.
Проценты, величина которых меньше 100, обозначают долю от исходного числа, больше 100 — превышение исходного числа.Для удобства в использовании проценты записывают обычно в виде чисел от 1 до 100.
Просто чаще всего мы сталкиваемся с величинами именно из этого диапазона. Как и у любого числа, у процентов тоже бывают десятые, сотые и прочие доли.
Наиболее часто они встречаются при работе с финансами и другими экономическими операциями, а также при представлении нескольких величин, составляющих части целого.
Теперь займемся непосредственно переводом процента в число. Это совсем не сложно. Как уже говорилось выше, 1% является сотой долей от целого. Целое есть единица, значит 1% = 0.01. Таким образом, чтобы перевести процент в число, нужно данное количество процентов разделить на 100, или, другими словами. сдвинуть запятую в данном числе на два знака влево, то есть на два порядка.
Функции для работы с процентами также есть практически в любом, даже самом простом калькуляторе. но, как вы можете видеть, данная операция является очень простой и не требует никаких особых усилий или знаний в области математики. Фактически, нужно запомнить единственную формулу.
Полученная в результате этого действия дробь будет десятичной, а её, в свою очередь, можно перевести в обыкновенную, представив как значимые цифры десятичной дроби, делённые на 10 в соответствующей степени. Десятичные дроби вообще очень хорошо воспринимаются и записываются на слух, скорей всего именно стало поводом использования 10 во второй степени, то есть 100, как основной единицей процента.
Также верно будет и обратное действие (попробуйте преобразовать данный пример справа налево).































