Калькулятор вклада с капитализацией, пополнением и частичным снятием, пролонгацией

Считаем процент от суммы вклада

Напомню, что проценты по банковскому вкладу могут быть простыми и сложными.

В первом случае банк начисляет доход на начальную сумму депозита. То есть, каждый месяц/квартал/год вкладчик получает от банка один и тот же «бонус».

Схема со сложными процентами для вкладчика выгоднее. Начисленный за месяц доход «плюсуется» к сумме вклада. И уже в следующем периоде процент будет насчитываться на большую сумму. А в следующем – на еще большую и так далее. На «длинных» сроках (10-20 лет) сложные проценты творят настоящие чудеса!

Конечно, формулы расчета для простых и сложных процентов отличаются друг от друга.

Рассмотрим их на конкретном примере.

Доходность по вкладу с простыми процентами

Сумма % = (вклад*ставка*дней в расчетном периоде)/(дней в году*100)

Пример. Валера открыл вклад на сумму 20 000 рублей под 9% годовых на один год.

Рассчитаем доходность вклада за год, месяц, неделю и один день.

Сумма процентов за год = (20 000*9*365)/(365*100) = 1800 рублей

Понятно, что в нашем примере годовую доходность можно было посчитать гораздо проще: 20 000*0,09. И в результате получить те же самые 1800 рублей. Но раз решили считать по формуле, то и будем считать по ней. Главное – понять логику.

Сумма процентов за месяц (июнь) = (20 000*9*30)/(365*100) = 148 рублей

Сумма процентов за неделю = (20 000*9*7)/(365*100) = 34,5 рублей

Сумма процентов за день = (20 000*9*1)/(365*100) = 5 рублей

Согласитесь, формула простых процентов элементарна. Она позволяет рассчитать доходность по вкладу за любое количество дней.

Доходность по вкладу со сложными процентами

Усложняем пример. Формула расчета сложных процентов уж чуть «мудреней», чем в предыдущем варианте. Калькулятор должен иметь функцию «степень». Как вариант, можно использовать опцию степень в таблице Excel.

Сумма % = вклад*(1+ ставка за период капитализации)число капитализаций — вклад
Ставка за период капитализации = (годовая ставка*дни в периоде капитализации)/(число дней в году*100)

Вернемся к нашему примеру. Валера разместил на банковском вкладе те же 20 000 рублей под 9% годовых. Но в этот раз — с ежемесячной капитализацией процентов.

Сначала посчитаем ставку за период капитализации. По условиям вклада проценты начисляются и «плюсуются» к депозиту один раз в месяц. Значит, в периоде капитализации у нас 30 дней.

Таким образом, ставка за период капитализации = (9*30)/(365*100) = 0,0074%

А теперь считаем, сколько наш вклад принесет в виде процентов за разные периоды.

Сумма процентов за год = 20 000*(1+0,0074) 12 – 20 000 = 1 850 рублей

В степень «12» мы возводим, потому что год включает двенадцать периодов капитализации.

Как видите, даже на такой символической сумме и коротком сроке разница в доходности вклада с простыми и сложными процентами составляет 50 рублей.

Сумма процентов за полгода = 20 000*(1+0,0074) 6 – 20 000 = 905 рублей

Сумма процентов за квартал = 20 000*(1+0,0074) 3 – 20 000 = 447 рублей

Сумма процентов за месяц = 20 000*(1+0,0074) 1 – 20 000 = 148 рублей

Вкладчик получит все те же 148 рублей и с простыми, и со сложными процентами. Расхождения в доходности начнутся со второго месяца. И чем длиннее срок депозита – тем существенней будет разница.

Пока мы не отошли далеко от темы сложных процентов, давайте проверим, насколько справедлива одна из рекомендаций финансовых консультантов. Я имею в виду совет выбирать вклады с капитализацией процентов не раз в полгода или квартал, а раз в месяц.

Предположим, наш условный Валера оформил депозит на ту же сумму, срок и под ту же ставку, но с капитализацией процентов раз в полгода.

Для начала нам придется пересчитать ставку за период капитализации. Ведь теперь этот период составляет не 30 дней (месяц), а 182 дня (полгода).

Ставка = (9*182)/(365*100) = 0,0449%

Теперь считаем доходность по вкладу за год.

Сумма процентов за год = 20 000*(1+0,0449) 2 – 20 000 = 1 836 рублей

Вывод: при прочих равных условиях полугодовая капитализация принесет Валере на 14 рублей меньше, чем ежемесячная (1850 – 1836).

Понимаю, что разница совсем невелика. Но ведь и другие исходные данные у нас символические. На крупных суммах и длинных сроках 14 рублей превратятся в тысячи и миллионы.

Виды процентных ставок по вкладам в банках

Открывая депозит в банке, у вас есть возможность решить, что вы хотите делать с начисляемыми дивидендами – выводить их на карту или прибавлять к сумме первоначального вклада, тем самым капитализируя его. В зависимости от того, какой вариант вы выберете, такой будет и формула расчета процентов. Если вы хорошо помните школьную математику, то вы знаете, что проценты бывают простыми, а бывают сложными.

Как начисляются простые проценты?

Итак, простая ставка по депозитам рассчитывается следующим образом:

Для удобства понимания давайте разберем такой пример: вы открываете в банке депозит на сумму в 50 000 рублей на 1 год с простым начислением процентов. Ставка % составляет 11,5%. Пользуясь вышеуказанной формулой, получается, что через год, после того как будет закрыт ваш депозит, вы заработаете:

В данном случае проценты не будут прибавляться к телу депозита, а каждый месяц (раз в полгода или раз в год) будут выводиться на другой ваш счет. Очень выгодно в таком случае пользоваться ежемесячным выводом процентов на дебетовые карты с начислением процентов на остаток. Если вы не успеваете потратить заработанные на депозите средства, на них будет начислен % по вашей карте.

Как начисляются сложные проценты?

Расчет сложных процентов по вкладу несколько сложнее и интереснее. Однако, прежде, чем мы приступим к его изучению, я предлагаю вам выяснить, в каких случаях мы имеем дело со сложной ставкой.

Открывая в банке депозит, вы вправе решать, прибавлять к нему полученные проценты или выводить их на другой счет. В случае, если вы выбираете первый вариант, по вашему вкладу начисляется сложный процент. То есть, в каждом последующем периоде % начисляются на большую сумму, нежели в предыдущем, тем самым ускоряя рост размера депозита.

Это присоединение выплат по депозиту к первоначальной сумме вклада очень важно, поскольку сумма накоплений растет все быстрее и быстрее. Причем, моделью роста выступает не арифметическая прогрессия, а экспонента

Для сравнения давайте возьмем расчет простых и сложных процентов по одному и тому же вкладу. Условно положим на счёт 100 000 рублей под 10% годовых. В конце расчетного периода по простой ставке мы получим:

100 000 * 10 / 100 = 10 000 рублей;

Чтобы посчитать доходность вкладов с капитализацией выведем общую формулу:

Формула сложных процентов представлена ниже:

Переменные означают следующее,

Рассчитываем наш пример:

100 000 * (1+0,833*365 / 100*365)^12 = 10 466,92 рублей

Таким образом, один и тот же депозит, положенный в банк на разных условиях, может принести как 10 000 рублей чистой прибыли, так и 10 466 рублей.

В последнем случае мы имеем дело с капитализацией депозита – добавлением начисленных % к телу депозита. Как результат, получаем рост первоначальной суммы инвестиции и начисление % на увеличенную сумму.

Чтобы не считать доходность депозита вручную, советую вам воспользоваться калькулятором сложных процентов. В нем вы сможете указать суммы регулярных довложений за определенный период. Найти такой калькулятор можно на моем сайте с правой стороны, в сайдбаре, во вкладке «Калькулятор доходности».

Как начисляется эффективная ставка?

Ну а теперь давайте разберемся с эффективной процентной ставкой по депозиту, чтобы собрать в голове полную картинку банковских предложений.

Эффективной ставкой принято называть ставку, дающую равнозначный доход по идентичному депозиту без капитализации процентов. То есть, предположим, что вы открываете счёт в размере 50 000 на год под 8% годовых с условием капитализации. Проводим расчет по уже известной нам формуле и получаем:

50 000 * (1+0,6666*365/100*365) 12 = 54 150 рублей.

А теперь смотрим на предложение в соседнем банке. Здесь вы можете открыть тот же самый депозит, но без капитализации, зато под 8,3% годовых. Такое предложение позволит вам получить точно такой же доход, как в случае с капитализацией.

(50 000 * 8,3 * 365/365) / 100 = 4 150 рублей.

Чтобы быстро рассчитать эффективную ставку по депозиту, достаточно сделать следующее:

Именно эти 8,3% и являются нашей эффективной годовой ставкой по депозиту с ежемесячной капитализацией. То есть, если вклад без прибавления процентов к телу депозита будет иметь ставку, превышающую 8,3%, то такое вложение будет для нас более выгодно, нежели депозит с 8% годовых и ежемесячной капитализацией. Не забываем, что в случае с вкладом с 8.3% годовых, ежемесячный процент можно перевести на дебетовую карту с начислением на остаток, в этом случае этот вклад будет выгоднее.

Сложные проценты

РешитьСложная процентная ставка наращенияm=12m=4S=P·(1+im)m·nсмешанным методомn

Современная стоимость Р величины S находится в случае сложной процентной ставки по формуле:
P=S(1+i)n

Примеры задач на сложные проценты

Какой величины достигнет долг, равный P = 1 млн.руб., через n = 5 лет при росте по сложной ставке i = 15,5% годовых, если проценты начисляются раз в год, ежемесячно, поквартально и два раза в год?
1) Сложные проценты начисляются раз в год:
2) Сложные проценты начисляются два раза в год:
S=1 000 000·(1+0,1552)2·5 = 2 109 467,26 руб.
3) Сложные проценты начисляются 4 раза в год (поквартально):
S=1 000 000·(1+0,1554)4·5 = 2 139 049,01 руб.
4) Сложные проценты начисляются ежемесячно (12 раз в год):
S=1 000 000·(1+0,15512)12·5 = 2 159 847,20 руб.
Через n = 5 лет предприятию будет выплачена сумма S = 1 млн.руб. Определить ее современную стоимость при условии, что применяется ставка сложных процентов i = 10% годовых.
P=S(1+i)n
P=1 000 000(1+0,1)5 = 620 921,32 руб.
Если проценты начислялись ежеквартально.
P=S(1+im)m·n
P=1 000 000(1+0,14)4·5 = 610 270,94 руб.
Определить современную стоимость S = 20 тыс.руб., которые должны быть выплачены через четыре года (n = 4). В течение этого периода на первоначальную сумму начислялись сложные проценты по i = 8 %годовых: а)ежегодно; б)ежеквартально.
P=S(1+i)n
P=20 000(1+0,08)4 = 14 568,92 руб.
Если проценты начислялись ежеквартально.
P=S(1+im)m·n
P=20 000(1+0,084)4·4 = 14 570 руб.
За взятые в долг деньги под сложную процентную ставку i=35% годовых должник обязан уплатить кредитору 30 тыс. руб. 1 июля 1997 г. Какую сумму необходимо уплатить должнику, если он вернет долг: а) 1 января 1997 г.; б) 1 января 1998 г.; в) 1 июля 1999 г.?
Количество дней в 1997 году: T=365.
а) 1 января 1997 г.;
Эта дата ранее 1 июля 1997 г., поэтому речь идет о поиске P (S=30000). Количество дней между 1 января 1997 г. и 1 июля 1997 г. составляет d=181 дн..
б) 1 января 1998 г.;
Эта дата позже 1 июля 1997 г., поэтому находим S (P=30000). d1=01.07.1997 и d2=01.01.1998.
в) 1 июля 1999 г.Количество лет между 1 июля 1997 г. и 1 июля 1999 г. составляет n=2 года.
S=P·(1+i)n=30000·(1+0.35)2 = 54 675 руб.

Платежи и проценты по кредиту

Тип платежа соискатель выбирает сам, исходя из периодичности и размера личных финансовых поступлений. Аннуитетные и дифференцированные выплаты имеют существенные отличия, которые определяют их достоинства и недостатки.

Аннуитетный

Клиент совершает фиксированные ежемесячные взносы, первая часть которых идёт на погашение процентов по договору, вторая – уменьшает тело кредита. Проценты начисляются на фактическую сумму долга, а она с каждым периодом уменьшается, в последующих выплатах соотношение частей будет изменяться. При этом сумма основного платежа останется неизменной.

Кредитный калькулятор при выборе аннуитета по заданным соискателем параметрам рассчитывает:

Процентную ставку за платёжный период, чаще всего это 1 месяц (ПСМ). Вычисляется следующим образом: ПСГ/100/12 (количество месяцев в году).

Коэффициент аннуитета (КА) по формуле, где * — степень, равная общему количеству платежей:

ПСМ x (1 + ПСМ) *

(1 + ПСМ) * — 1

Сумму аннуитетного платежа (АП), которая равна: ОД x КА.

Проценты (СП) по формуле, где СЗ – размер фактической задолженности, которая в первом взносе всегда равна ОД: СЗ x ПСМ.

Их долю (ДСП): АП – СП.

Долю погашения ОД (ДОД): АП – ДСП.

Анализ расчётов, диаграммы и графика онлайн-сервиса Сбербанка покажет, что аннуитетный тип наиболее выгоден для финансового учреждения (переплата выше, чем при дифференцированном). Но он удобен для клиентов, которые получают стабильный фиксированный доход.

Дифференцированный

На практике данный тип платежей применяется для ипотечных кредитов, но нередко банки используют его для потребительских программ. Главное отличие – стабильное уменьшение суммы ежемесячного платежа на протяжении всего срока действия договора. Основная финансовая нагрузка приходится на первые месяцы. Доля погашения ОД остаётся фиксированной для каждого периода, а размер процентов уменьшается.

Алгоритм расчёта параметров кредита с дифференцированным типом выплат для онлайн-калькулятора выглядит проще и состоит из вычислений:

Доли платежей, ежемесячно погашающих ОД – соотношение ОД и количества периодов срока кредитования (количество месяцев).
Доли процентов: произведение фактического ОД на ПСМ.
Размер дифференцированного платежа (ДП) для каждого периода: сумма доли процентов и ОД.

Проценты так же начисляются на остаток ОД, то есть их сумма становится меньше с каждым периодом.

Анализ результатов кредитного калькулятора покажет, что при строгом соблюдении графика выплат, дифференцированный тип предпочтительнее для некоторых клиентов, так как уменьшает переплату по продукту.

С помощью формул, соискатель может провести все расчёты по кредиту самостоятельно, но проще доверить эту работу кредитному калькулятору.

⚖ Разница между сложными и простыми процентами

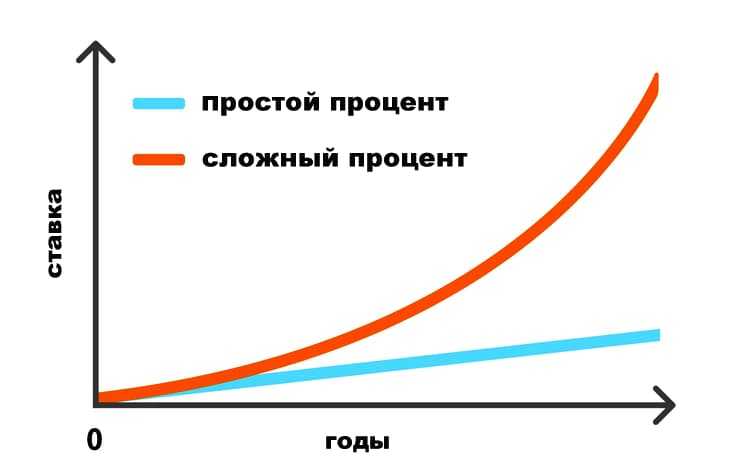
Главное различие между процентами в том, на что они начисляются. При использовании простого процента всегда берется за основу изначальная сумма. При этом совершенно не имеет значение, какой вы совершаете расчет для одного или трех лет — поскольку сумма все равно всегда будет одинаковая.

Что касается сложного %, то здесь основа вычислений является предыдущими вычислениями. Другими словами, за основу расчетов текущего года берется то, что рассчитывалось для прошлых лет.

Если еще короче, то при сложном % основа всегда будет различной, а при простом %, наоборот, одинаковой.

При сложном проценте все доходы начисляются каждый год, а при простом % — это происходит всего один раз, как правило, в конце всего срока.

При расчете сложного процента постоянно учитывается изначальная сумма, а также доход с каждого конкретного года, а при расчете простого % — учитывается исключительно изначальная сумма.

При использовании сложного процента вся прибыль будет всегда различной. Она будет всегда увеличиваться, а при использовании простого % прибыль будет стабильной и всегда одинаковой.

Главное преимущество сложного процента в том, что при его использовании в конце всех сроков вы можете получить намного больше денег, чем при использовании простого процента.

На расчет сложных процентов всегда оказывают влияние 4 фактора:

начальная сумма;
периодичность всего пополнения;
ставка процента;
период инвестирования.

Вопросы и ответы

А также советуем обратить внимание на ответы на часто задаваемые вопросы относительно расчётов со сложным процентом

Где применяются сложные проценты в повседневной жизни?

Сложный процент является простым способом максимально увеличить прибыль ваших вложений. Чтобы его применить, нужно не совершать трат, а снова делать вклады по ценным бумагам. Например, проценты по облигациям или дивиденды по акциям. Также сложный процент обычно применяется в тот момент, когда вы кладете деньги на депозит в банке.

Что такое реинвестирование?

Это понятие рассматривается, как дополнительное вложение капитала в инвестиции за счет полученной прибыли или доходов от них. Другими словами — это получение дохода на повторно инвестированных доходах от первоначальных активов.

Сравнительный анализ

Для того чтобы стало понятнее, что именно ждет россиян в связи с введением в действие ст. 214.2, сделаем сравнительный анализ между тем, что было, и тем, как будет.

Итак, до 2020 года действуют старые положения Налогового кодекса относительно уплаты налогов с дохода от рублевых вкладов.

В соответствии со старыми положениями закона налог с дохода по вкладам следовало оплатить в случае, если банковская ставка по вкладу превышала ключевую ставку ЦБ по показателю плюс 5 процентных пунктов. Налог подлежал уплате с суммы, превышающей этот лимит.

Например, при ключевой ставке ЦБ в 6% добавление пяти процентных пунктов в сумме дает 11 процентов годовых. Поскольку таких ставок по вкладам физических лиц не существует, налог не платил никто.

То есть определение налоговой базы было привязано к процентной ставке банка, ключевой ставке ЦБ и добавочным процентным пунктам. Поскольку при любом раскладе арифметические действия давали несуществующую ставку, то ст. 214.2 была практически недействующей, вне зависимости от того, миллиардный или миллионный был вклад.

Исходя из необходимости модификации «недееспособной» статьи НК РФ, законодатель разработал новые положения взимания налогов с доходов по вкладам граждан.

Для этого статья 214.2 НК РФ в новой редакции установила ряд изменений, а именно:

налог был «отвязан» от процентов по банковскому вкладу;
банкам была вменена обязанность сообщать в налоговые органы обо всех вкладах граждан;
перед налоговыми органами поставили задачу ведения суммарного учета всех вкладов по каждому конкретно вкладчику;
налог был привязан к реальному доходу вкладчика от процентной ставки по вкладу. С целью установления дохода налоговые органы должны суммировать доходы от каждого вклада гражданина, если процентная ставка по ним составляет более 1 %;
был установлен лимит дохода. Арифметически лимит дохода устанавливается путем умножения общей суммы вкладов на действующую ключевую ставку ЦБ РФ;
была установлена единая налоговая ставка по доходам от вкладов, равная 13% и для резидентов, и для нерезидентов РФ.

От чего зависит размер процентной ставки

Чтобы понять, от чего зависит размер процентной ставки, нужно отметить, что разные виды вкладов имеют разные предложения, формирование которых происходит следующим образом.

Зависимость от ключевой ставки

Ставки, основанные на законодательном обеспечении регулируются Центральным Банком Российской Федерации. Размер этих ставок зависит от того, какую ключевую ставку предлагает Центробанк другим банкам, выдавая последним кредиты. К примеру, с 1 января 2016 года ставка рефинансирования соответствует значению ключевой ставки ЦБ РФ. На 12 апреля 2020 года она составляет 6% годовых. Актуальные ставки вы можете посмотреть на официальном сайте ЦБ РФ.

Данные ставок Центрального Банка являются своеобразным индикатором состояния экономики и рассказывают нам об уровне инфляции в стране. Предложение банка не может превосходить ставки ЦБ России на 5 пунктов. То есть, если Центробанк выдает кредиты под 10%, то банк не может предложить физлицам более 15%. Если же вы все-таки получили предложение с более высокой ставкой, то приготовьтесь заплатить государству подоходный налог в размере 35% от суммы, превышающей эту доходность.

Предложение денег в государстве

Думаю, каждый финансово образованный человек понимает, что недостаток денежной массы вызывает дефицит денег и приводит к тому, что кредиты начинают дорожать, а ставки по депозитам расти. Если, к примеру, вы умеете экономить деньги и открываете счет в банке, в то время, как ваш сосед Анатолий живет в кредит, то вам банк предложит более высокие ставки по депозиту, а Анатолию – по кредиту.

Внимательно следите за новостями и научитесь их правильно анализировать. Если вы слышите, что Центральный Банк планирует напечатать деньги, чтобы выдать их в большем объеме банкам, то нам всем стоит готовиться к увеличению инфляции и снижению депозитных ставок. Если же государство проводит масштабное заимствование средств на своем внутреннем рынке, то это означает, что в стране происходит стерилизация денежной массы или, иными словами, сокращение предложения денег. В результате таких процессов мы получаем рост депозитных ставок.

Макро- и микроэкономические факторы

Когда экономика активно развивается, предприятия активно берут кредиты для своего развития, расширения производства и улучшения материально-технического оснащения. Банки нуждаются в привлечении денег населения, а потому предлагают своим капиталовкладчикам более высокие процентные ставки по депозитам. Если же экономика оказывается в рецессии, то спрос на деньги падает, а банковские проценты по вкладам снижаются.

Как видите, размер процентных ставок зависит от целого спектра составляющих: начиная от самих банков и заканчивая состоянием экономики государства в целом.

Как рассчитать ежедневный процент по накопительному вкладу

Если процент простой, то для расчета не потребуется знать формулы и использовать онлайн-сервисы. Ежедневная ставка равна величине процентов, установленных в банке в момент размещения вклада, поделенной на 365 или 366 дней (в зависимости от года). Но этот вариант не действует в нескольких случаях:

при капитализации — проценты увеличивают сумму накопительного счета с того дня, когда назначена их выплата;
при сложном проценте — когда в первые месяцы ставка выше, чем в последующие;
при начислении процентов не за каждый день действия вклада, а всего раз в месяц на наименьшую сумму, размещенную на депозите.

Из-за этих нюансов расчет стоит автоматизировать, используя калькулятор вклада. В этом случае можно получить достоверные цифры, не путаясь в формулах. Для расчета потребуется заполнить форму калькулятора, указав:

частоту начисления процентов;
сумму депозита;
установленную банком ставку;
возможность капитализации, пополнения или снятия.

При использовании онлайн-калькулятора, вычисления будут предварительными. Даже если использовать для расчетов материалы, размещенные на сайте банка. Это связано с тем, что по накопительным счетам ставка может измениться, снятия и пополнения счета часто происходят не по плану.

После открытия вклада клиенту доступна расширенная статистика, в которой можно посмотреть, как происходят начисления процентов, и куда была зачислена их сумма. Для вкладов с капитализацией характерно увеличение размера депозита, а для остальных выплата на дебетовый счет. Если непонятны расчеты банка, можно уточнить их в контактном центре. Для этого потребуется знать название вклада и срок.

Точнее вычисления поможет сделать калькулятор вклада. В нем учтены особенности применения тарифов. Универсальный инструмент на портале Finanso подойдет для того, чтобы предварительно рассчитать доход, сравнить несколько предложений от различных банков.

Калькулятор вклада с капитализацией, пополнением, частичным снятием, пролонгацией

Считаем процент от суммы вклада

Доходность по вкладу с простыми процентами

Доходность по вкладу со сложными процентами