Глава 1. военная топография в допризывной подготовке молодежи

Центральный угол.

Основные определения

Напомним определение окружности. Сейчас мы дадим определение с ошибкой, задача – найти эту ошибку.

Определение:

Окружностью с центром в точке О и радиусом R называют множество точек плоскости, удаленных от одной точки – центра окружности О – на расстояние R.

Очевидно, что ошибка – пропущенное важное слово всех, то есть окружность – множество всех точек, равноудаленных от ее центра. Например, вершины A, B, C, D квадрата – это множество точек, равноудаленных от центра квадрата, но это не есть окружность (рис

1)

Например, вершины A, B, C, D квадрата – это множество точек, равноудаленных от центра квадрата, но это не есть окружность (рис. 1).

Рис. 1. Квадрат

Вспомним важные элементы окружности:

Дуга ;

Угол  – центральный угол;

Точка О – центр окружности.

Имеем дугу и соответствующий центральный угол (рис. 2).

Рис. 2. Элементы окружности

Понятие градусной меры дуги

Рассмотрим понятие градусной меры дуги.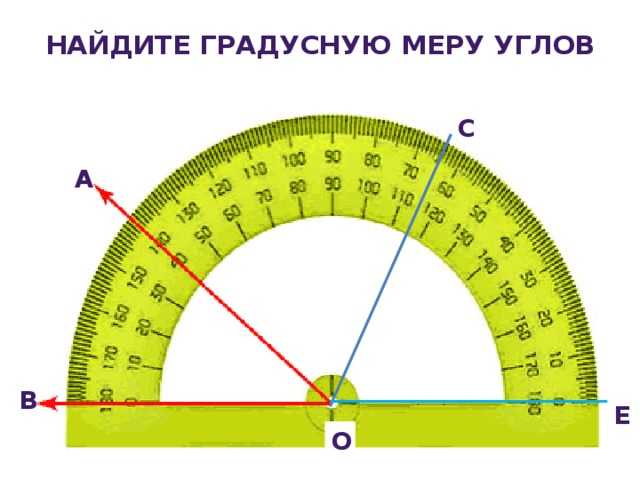

Задана окружность с центром О. Дуга ALB не больше полуокружности; дуга AМB больше полуокружности.

Градусной мерой дуги ALB называется градусная мера соответствующего центрального угла – .

Для дуги, большей полуокружности, градусной мерой будет следующая разность:

 (рис. 3).

Рис. 3. Градусная мера дуги

Две дуги  и  вместе составляют целую окружность, запишем это:

Таким образом, градусная мера окружности – это .

Решение примеров

Задана окружность с центром О, диаметром АВ, радиусом, перпендикулярным диаметру, ОС, радиусом ОМ, который составляет с ОС угол .

Дуга  – пол-окружности;

Дуга  – четверть окружности, угол  прямой;

Дуга ;

Дуга  состоит из двух дуг, ее градусная мера равна сумме градусных мер двух дуг: ;

Дуга  больше полуокружности, значит, ее градусная мера – это разность: .

Рис. 4. Иллюстрация к примерам

Каждая дуга стягивается своей хордой, во многих задачах требуется найти длину этой хорды.

Пример:

Радиус окружности с центром О – 16 см. Найдите хорду АВ, если:

а)

б)

в)

Решение:

Итак, в случае а . Треугольник  равнобедренный, стороны ОА и ОВ равны как радиусы окружности. Углы при основании равны и сумма их равна , значит, на каждый из углов приходится , таким образом, в треугольнике  все углы составляют , а значит, этот треугольник равносторонний и сторона АВ равна также радиусу окружности, то есть 16 см (рис. 5).

Рис. 5. Иллюстрация к случаю а

В случае б центральный угол  составляет . Рассмотрим прямоугольный равнобедренный треугольник  и применим теорему Пифагора, чтобы найти его гипотенузу: . Нашли  см (рис. 6).

Рис. 6. Иллюстрация к случаю б

В случае в , значит, в данном случае АВ является диаметром окружности. Мы знаем, что диаметр равен двум радиусам, радиус нам известен. Таким образом,  см (рис. 7).

Рис. 7. Иллюстрация к случаю в

Выводы по уроку

Итак, мы узнали, что такое центральный угол, познакомились с понятием градусной меры дуги окружности.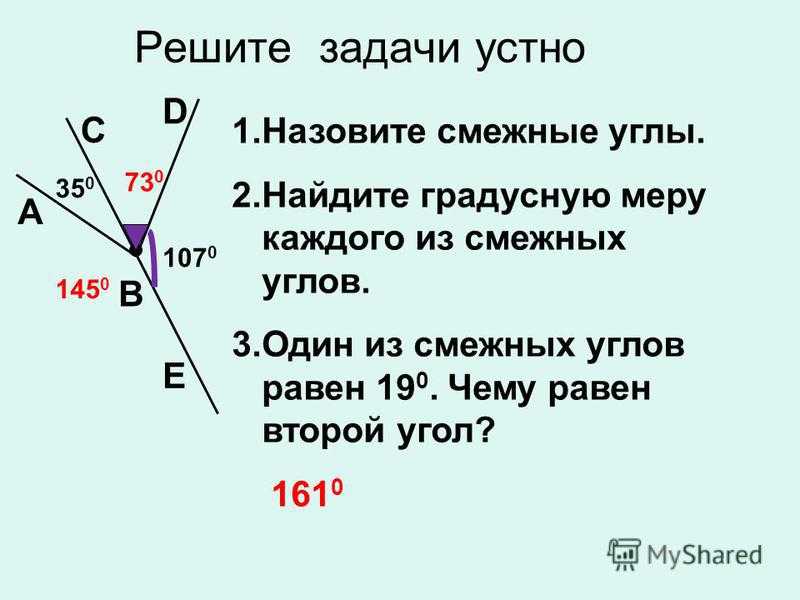

Список литературы

1. Александров А.Д. и др. Геометрия 8 класс. – М.: Просвещение, 2006.
2. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия 8. – М.: Просвещение, 2011.
3. Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Uztest.ru (Источник).
2. Raal100.narod.ru (Источник).
3. Uztest.ru (Источник).

Домашнее задание

1. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др., Геометрия 7–9, № 649, № 651, № 652, с. 73.

Измерение углов: выбираем «эталон»

Подумайте о торте, который разрезается на равные доли, чтобы каждому, сидящему за столом, достался кусочек. Окружность — это торт, и «порезать» ее мы можем как угодно: на пять кусочков, на шесть и так далее.

Иными словами, окружность делится на сколь угодно частей: на десять, пятнадцать, хоть на двадцать тысяч. Поскольку мы вольны выбирать любое число из возможных, оно должно быть удобным математически.  

{"questions":[{"content":"Кое-что проверим перед тем, как продолжить обсуждать деление окружности на части. Что из себя представляет множество натуральных чисел $\\mathbb{N}$? `choice-1`","widgets":{"choice-1":{"type":"choice","options":["Множество чисел, возникающих естественным образом при счёте (1, 2, 3, 4 и так далее).","Числа, которые можно представить в виде рациональной дроби $\\frac{a}{b}$."],"answer":}},"explanation":""}]}

Почему окружность можно разбивать произвольно?

Единицу можно представить в виде обыкновенной дроби:

$$\frac{a}{b},$$

где $a=b$ и $a\in{\mathbb{N}}$, $b\in{\mathbb{N}}$

Величины $a$ и $b$ принадлежат множеству натуральных чисел $\mathbb{N}$, ведь представлять единицу множеством иррациональных чисел $\mathbb{Q}$ (например, $\frac{\sqrt{2}}{\sqrt{2}}$) — занятие, потенциально обрекающее математиков на мучения.

Отрицательные числа нас тоже не интересуют, ведь измерение углов и его результат (пока что) — значение со знаком «плюс». Вспомните измерение отрезков и аксиому, что длина всякого отрезка всегда больше нуля.

Итого, получается $\frac{1}{1}$, $\frac{2}{2}$, $\frac{3}{3}$, $\frac{4}{4}$, … $=1$.   

На сколько бы частей вы ни разрезали торт, сложив все кусочки, вы получаете единицу торта. Торт может быть огромным, как планета Марс. Он может быть маленьким, подобно спичечному коробку. Однако «собрав в кучу» все доли — хоть большого, хоть маленького, — вы неизменно получаете единицу.  

Единица измерения углов: «супер»-число

Время, за которое Земля по своей орбите полностью огибает Солнце, именуется годом и состоит из 365 дней. Древние астрономы хитрыми вычислениями смогли данную цифру вывести буквально на палках. Правда, точность их расчетов не учла несколько дней, и вышло у них число 360. Может, это было намеренное округление. Как таковая письменность в те времена еще не возникла, так что узнать наверняка, как оно было, возможности нет.

А еще 360 — это «супер»-число. Оно делится на:

2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120 и 180

{"questions":}

В минуте — 60 секунд, в часе — 60 минут, в сутках — 24 часа. В году — 12 месяцев. Время тесно связано с движением нашей планеты по окружности. Так что 360 — это отличный выбор для «разрезания» окружности. Оно не только, можно сказать, подарено нам природой, но еще и математически удобно. Как раз то, что мы искали!

Измерение величин «Чужими единицами»

На самом деле бывает, когда мы одни величины измеряем единицами, казалось бы, для них не предназначенными, «чужими» единицами.

Можно ли измерить расстояние в минутах? Да, мы часто используем этот способ. «От моего дома до школы 5 минут». Если быть точнее, то «5 минут пешком». Мы здесь используем известную всем величину – скорость пешехода. И величина «5 минут» на самом деле означает «расстояние, которое пешеход проходит за 5 минут». Скорость пешехода – 5 км/ч, 5 минут – это  часа, умножим одно на другое. Получаем примерно 400 метров. Не очень точно, зато удобно.

Точно по такому же принципу устроена другая единица измерения расстояния – световой год. Световой год – расстояние, которое проходит свет за 1 год. С помощью этой единицы меряют расстояния между звездами.

Очень распространенный пример использования «чужой» единицы измерения – это измерять вес в килограммах. На самом деле килограмм – единица измерения массы, а вес – это другая физическая величина. Если хотите подробнее узнать, в чем разница между массой и весом, и почему измерять вес в килограммах не верно, то наберите в поисковой системе «масса и вес» и получите множество пояснений по этому поводу.

Атмосферное давление мы до сих пор измеряем в миллиметрах (миллиметрах ртутного столба).

Хотя для угла есть свои «родные» единицы измерения – градусы, которые мы и проходим на этом уроке, все-таки его можно измерять и с помощью линейных величин, например сантиметров. Если нужно измерить угол , то можно достроить его до треугольника, так чтобы один угол был прямым, и разделить длину одной стороны на другую.

Получим величину угла , которая называется тангенсом.

Если увеличить треугольник, то ничего не изменится (см. Рис. 16).

Рис. 16. Тангенс

Ведь во сколько раз увеличилась одна сторона, во столько и вторая.

То есть величины часто можно измерять «чужими» единицами, но это чуть сложнее, там нужны некоторые дополнительные договоренности.

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Лекция:
Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности

Мерой угла
называют величину, на которую отклоняется некоторый луч относительно первоначального положения.

Мера угла может измеряться двумя величинами: градусами и радианами, отсюда и название единиц – градусная и радианная мера угла.

Градусная мера угла

Градусная мера дает возможность оценить, какое количество градусов, минут или секунд помещается в тот или иной угол.

Расчет углов в градусах производится с точки зрения того, что полный поворот луча – это 360°. Половина поворота 180° — развернутый угол, четверть – 90° — прямой угол и т.д.

Радианная мера угла

А теперь давайте же разберемся, что такое радианная мера угла. Как известно из физики, существуют дополнительные единицы. Например, для измерения температуры основной единицей являются Кельвины, а дополнительной градусы Цельсия. Для измерения длины мы используем метры, а англичане используют футы. Данный список можно продолжать и далее. Смысл в том, чтобы Вы поняли, что, кроме градусной меры измерения угла, существует радианная мера, которая так же имеет право на существование.

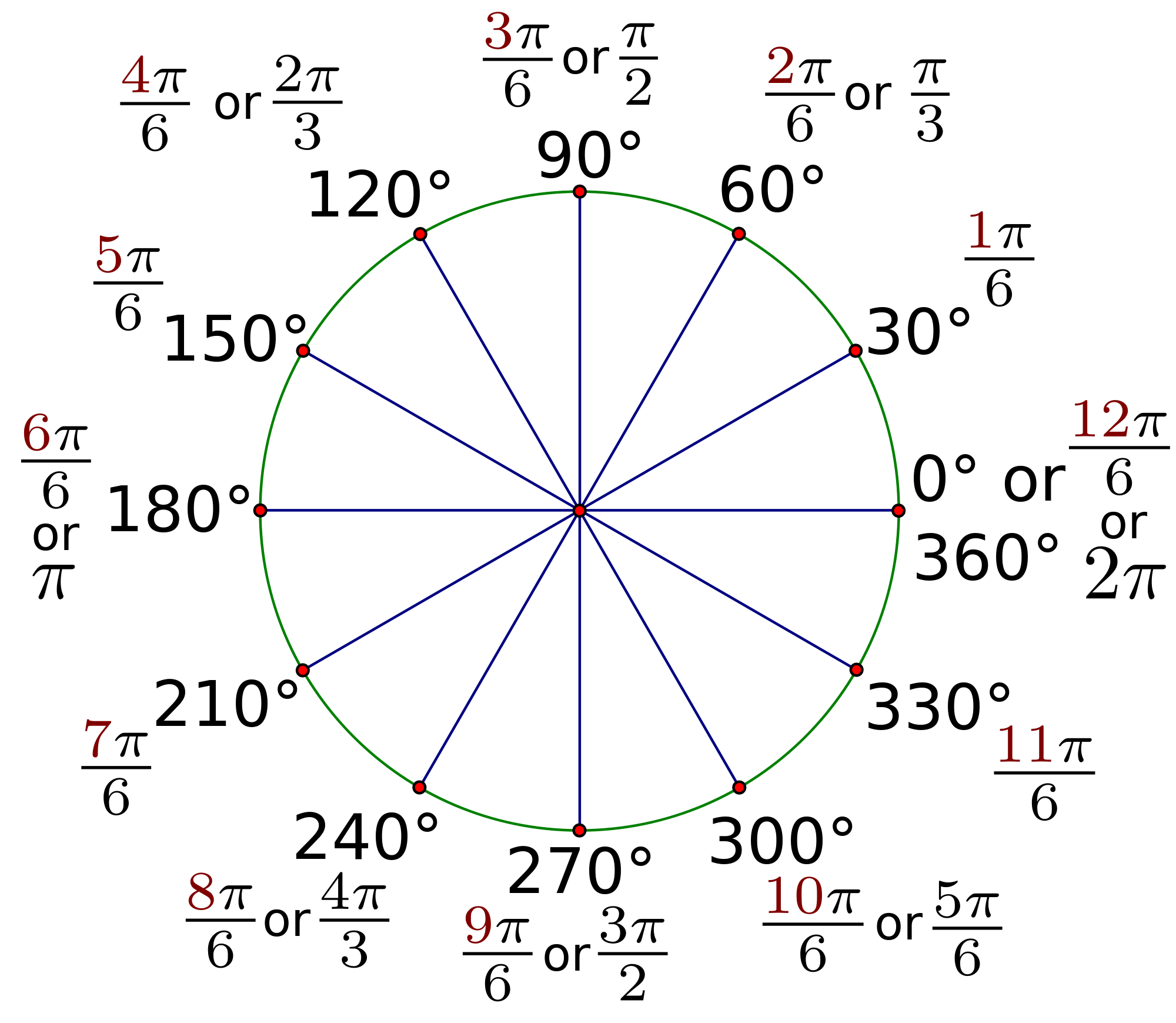
Для определения радианной меры угла используют окружность. Считается, что радианная мера – это длина дуги окружности, описанная центральным углом.

Напомним, что центральный угол – это угол, вершина которого находится в центре окружности, а лучи опираются на некоторую дугу.

Итак, угол в 1 рад имеет градусную меру в 57,3°. Радианная мера угла описывается либо натуральными числами, или же с использованием числа π ≈ 3,14.

Для геометрии удобнее использовать градусную меру угла, однако для тригонометрии используют радианную меру.

Углом называется фигура, которая состоит из точки — вершины угла и двух различных полупрямых, исходящих из этой точки, — сторон угла (рис. 14). Если стороны угла являются дополнительными полупрямыми, то угол называется развернутым.

Угол обозначается либо указанием его вершины, либо указанием его сторон, либо указанием трех точек: вершины и двух точек на сторонах угла. Слово «угол» иногда заменяют

символом Угол на рисунке 14 можно обозначить тремя способами:

Говорят, что луч с проходит между сторонами угла если он исходит из его вершины и пересекает какой-нибудь отрезок с концами на сторонах угла.

На рисунке 15 луч с проходит между сторонами угла так как он пересекает отрезок

В случае развернутого угла любой луч, исходящий из его вершины и отличный от его сторон, проходит между сторонами угла.

Углы измеряются в градусах. Если взять развернутый угол и разделить его на 180 равных углов то градусная мера каждого из этих углов называется градусом.

Основные свойства измерения углов выражены в следующей аксиоме:

Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

Это значит, что если луч с проходит между сторонами угла то угол равен сумме углов

Градусная мера угла находится при помощи транспортира.

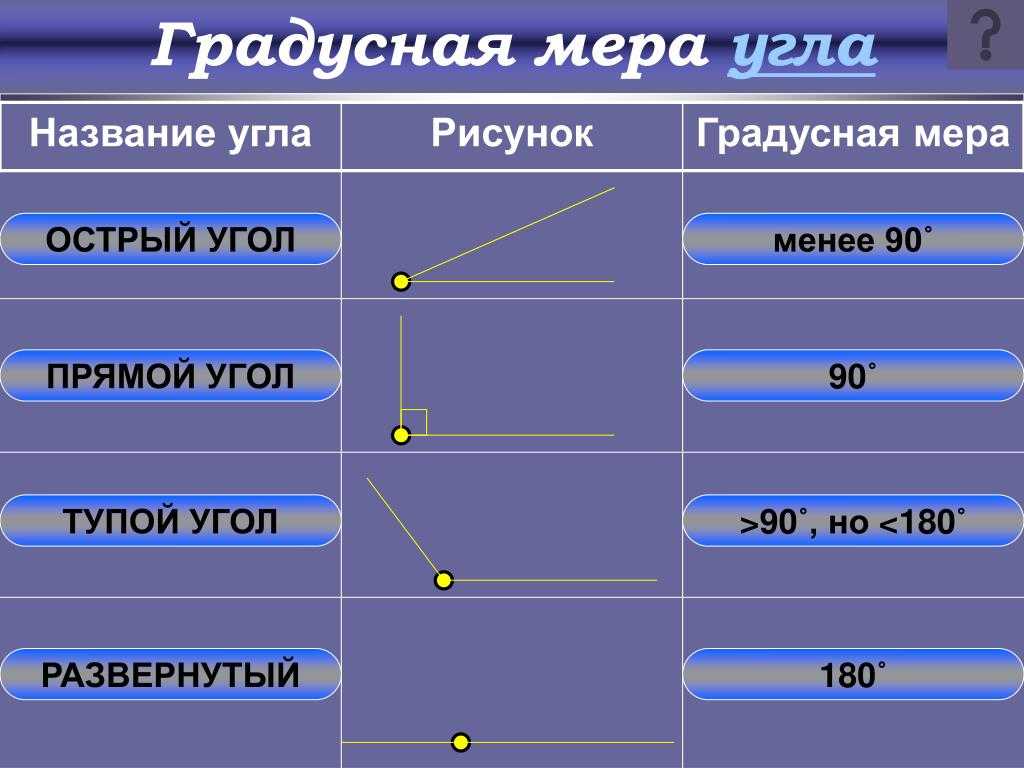
Угол, равный 90°, называется прямым углом. Угол, меньший 90°, называется острым углом. Угол, больший 90° и меньший 180°, называется тупым.

Сформулируем основное свойство откладывания углов.

От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.

Рассмотрим полупрямую а. Продлим ее за начальную точку А. Полученная прямая разбивает плоскость на две полуплоскости. На рисунке 16 показано, как с помощью транспортира отложить от полупрямой а в верхнюю полуплоскость угол с данной градусной мерой 60°.

Т. 1. 2. Если от данной полупрямой отложить в одну полуплоскость два угла, то сторона меньшего угла, отличная от данной полупрямой, проходит между сторонами большего угла.

Пусть — углы, отложенные от данной полупрямой а в одну полуплоскость, и пусть угол меньше угла . В теореме 1. 2 утверждается, что луч проходит между сторонами угла (рис. 17).

Биссектрисой угла называется луч, который исходит из его вершины, проходит между сторонами и делит угол пополам. На рисунке 18 луч — биссектриса угла

В геометрии существует понятие плоского угла. Плоским углом называется часть плоскости, ограниченная двумя различными лучами, исходящими из одной точки. Эти лучи называются сторонами угла. Существуют два плоских угла с данными сторонами. Они называются дополнительными. На рисунке 19 заштрихован один из плоских углов со сторонами а и

Градусная мера угла — формулировка

Градусная мера, в первую очередь, делает возможным измерение углов в геометрии.

Это число – показатель того, сколько градусов, минут и секунд содержится в данном угле. 

Примечание

Оно всегда больше нуля.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Обозначение

С помощью символов градусов ((º)), минут ((′)) и секунд ((″)).

В одном градусе содержится шестьдесят минут, в одной минуте — шестьдесят секунд.

Пример

(125º) (22′) (15″) (сто двадцать пять градусов, двадцать две минуты, пятнадцать секунд).

Примечание

Если настолько точно, как показано выше определить меру невозможно, пользуются дробной мерой градуса. Например, (123,5º).

Пример

Обозначение на чертеже:

Вычисление радианной меры угла

Теперь, когда мы разобрались с основными определениями тригонометрических функций, перейдем непосредственно к сегодняшней теме урока.

Для начала давайте рассмотрим угол в 180º. Тогда наш луч поддет в противоположном направлении. Точка В в нашем треугольнике высекает определенную дугу окружности. Назовем ее дуга BCBC. Ее легко посчитать по формуле длины окружности:

l=2πr

l=2\pi r

π˜3,14

\pi \tilde{\ }3,14. Но сейчас нас это не интересует. Поскольку наша окружность всегда имеет фиксированный радиус 1, то длина будет равна:

l=2π

l=2\pi

Однако 2π2\pi — это вся окружность, т. е. полный оборот. А мы если отступим на 180º, то получим только ее половину. Следовательно, дуга окружности будет равна:

l(180o)=2π2=π

l\left( 180{}^\text{o} \right)=\frac{2\pi }{2}=\pi

И вот тут возникает замечательный эффект. Дело в том, что один и тот же угол α\alpha мы можем обозначать как за 180º, т. е. использовать стандартную меру угла (а не радианную), так и длинной вот этой дуги, т. е. мы можем поставить углу α\alpha соответствующее число π\pi . Так вот это число π\pi , т. е. другими словами, угол, измеренный не в градусах, а в длине дуги, которую этот угол высекает. Называется это радианная мера угла и обозначается π\pi — радиан.

Сегодня же для того чтобы начать решать задачи на радианную меру и считать значение тригонометрических функций, просто запомните, что π\pi рад = 180º. Другими словами, если вам непривычно работать с радианными значениями, то везде, где вы видите в синусах, косинусах и тангенсах конструкцию π\pi , вы можете смело заменить это π на 180º и перейти к знакомой градусной от радианной меры. Давайте попробуем и сосчитаем первое выражение и найдем радианную меру:

sin π 4cos π 6tg π 3=2√2⋅3√2⋅3√=32√4\sin \frac{\text{ }\!\!\pi\!\!\text{ }}{4}\cos \frac{\text{ }\!\!\pi\!\!\text{ }}{6}tg\frac{\text{ }\!\!\pi\!\!\text{ }}{3}=\frac{\sqrt{2}}{2}\cdot \frac{\sqrt{3}}{2}\cdot \sqrt{3}=\frac{3\sqrt{2}}{4}

Давайте выпишем отдельно каждую из этих функций:

sin π 4=sin180∘4=sin45∘=2√2\sin \frac{\text{ }\!\!\pi\!\!\text{ }}{4}=\sin \frac{180{}^\circ }{4}=\sin 45{}^\circ =\frac{\sqrt{2}}{2}

cos π 6=cos180∘6=cos30∘=3√2\cos \frac{\text{ }\!\!\pi\!\!\text{ }}{6}=\cos \frac{180{}^\circ }{6}=\cos 30{}^\circ =\frac{\sqrt{3}}{2}

tg π 3=tg180∘3=tg60∘=3√tg\frac{\text{ }\!\!\pi\!\!\text{ }}{3}=tg\frac{180{}^\circ }{3}=tg60{}^\circ =\sqrt{3}

Теперь записываем все три множителя в единую конструкцию для нахождения радианного значения. Вот и все, мы получили ответ.

Переходим ко второму выражению и найдем радианную меру:

cos π 3sin π 4ctg π 6=12⋅2√2⋅3√=6√4\cos \frac{\text{ }\!\!\pi\!\!\text{ }}{3}\sin \frac{\text{ }\!\!\pi\!\!\text{ }}{4}ctg\frac{\text{ }\!\!\pi\!\!\text{ }}{6}=\frac{1}{2}\cdot \frac{\sqrt{2}}{2}\cdot \sqrt{3}=\frac{\sqrt{6}}{4}

Опять записываем каждую функцию отдельно:

cos π 3=cos60∘=12\cos \frac{\text{ }\!\!\pi\!\!\text{ }}{3}=\cos 60{}^\circ =\frac{1}{2}

sin π 4=sin45∘=2√2\sin \frac{\text{ }\!\!\pi\!\!\text{ }}{4}=\sin 45{}^\circ =\frac{\sqrt{2}}{2}

ctgπ6=ctg30∘=3√ctg\frac{\pi }{6}=ctg30{}^\circ =\sqrt{3}

Опять собираем все полученные числа.

Как видите, ничего сложно в радианных мерах угла нет. Если эта тема покажется вам слишком сложной, просто запомните, что π\pi рад = 180º, и везде, где вы видите π\pi , можете смело писать 180º.

Еще одним важным следствием нового определения тригонометрического круга является то, что синус, косинус и тангенс могут быть отрицательными. Если раньше все сводилось к длинам катетов и гипотенузы, то теперь перед нами абсциссы и ординаты некой точки. При этом помните, что откладывание угла всегда идет в направлении от оси OxOx к оси OyOy, причем идет речь именно о положительных направлениях этих осей.

Чтобы понять и навсегда запомнить, где находится положительное направление оси, просто помните правило: туда, куда указывает стрелка при х и при у, это и есть то самое положительное направление оси.

Вот это и все, о чем я хотел рассказать в сегодняшнем видеоуроке о радианных мерах. Если вы что-то не поняли, или если этот материал показался вам слишком сложным, то пересмотрите его еще раз, попробуйте выполнить всю последовательность вычислений на нахождения радианных значений, которую мы сегодня выполнили на уроке.  

1. Как быстро запомнить таблицу синусов и косинусов
2. Синус, косинус, тангенс, котангенс — геометрическая тригонометрия
3. Метод узлов в задаче B5
4. Тест к уроку «Сложение и вычитание дробей» (средний)
5. Иррациональное уравнение: учимся решать методом уединения корня
6. Задача B4: строительные бригады

Определение угла.

Угол является одной из важнейших фигур в геометрии. Определение угла дается через определение луча. В свою очередь представление о луче невозможно получить без знания таких геометрических фигур как точка, прямая и плоскость. Поэтому, перед знакомством с определением угла, рекомендуем освежить в памяти теорию из разделов прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.

Итак, будем отталкиваться от понятий точки, прямой на плоскости и плоскости.

Дадим сначала определение луча.

Пусть нам дана некоторая прямая на плоскости. Обозначим ее буквой a. Пусть O – некоторая точка прямой a. Точка O разделяет прямую a на две части. Каждая из этих частей вместе с точкой О называется лучом, а точка О называется началом луча. Еще можно услышать, что луч называют полупрямой.

Для краткости и удобства ввели следующие обозначения для лучей: луч обозначают либо малой латинской буквой (например, луч p или луч k), либо двумя большими латинскими буквами, первая из которых соответствует началу луча, а вторая обозначает некоторую точку этого луча (например, луч ОА или луч СD). Покажем изображение и обозначение лучей на чертеже.

Теперь мы можем дать первое определение угла.

Определение.

Угол – это плоская геометрическая фигура (то есть целиком лежащая в некоторой плоскости), которую составляют два несовпадающих луча с общим началом. Каждый из лучей называют стороной угла, общее начало сторон угла называют вершиной угла.

Возможен случай, когда стороны угла составляют прямую линию. Такой угол имеет свое название.

Определение.

Если обе стороны угла лежат на одной прямой, то такой угол называется развернутым.

Предлагаем Вашему вниманию графическую иллюстрацию развернутого угла.

Для обозначения угла используют значок угла «». Если стороны угла обозначены малыми латинскими буквами (например, одна сторона угла k, а другая h), то для обозначения этого угла после значка угла записывают подряд буквы, соответствующие сторонам, причем порядок записи значения не имеет (то есть, или ). Если стороны угла обозначены двумя большими латинскими буквами (к примеру, одна сторона угла OA, а вторая сторона угла OB), то угол обозначают следующим образом: после значка угла записывают три буквы, участвующие в обозначении сторон угла, причем буква, отвечающая вершине угла, располагается посередине (в нашем случае угол будет обозначен как или ). Если вершина угла не является вершиной еще какого-нибудь угла, то такой угол можно обозначать буквой, соответствующей вершине угла (например, ). Иногда можно видеть, что углы на чертежах отмечают цифрами (1, 2 и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.

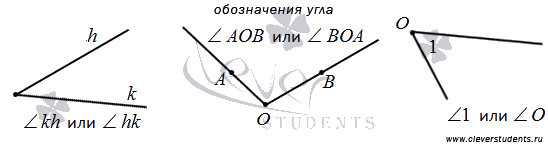
Любой угол разделяет плоскость на две части. При этом если угол не развернутый, то одну часть плоскости называют внутренней областью угла, а другую – внешней областью угла. Следующее изображение разъясняет, какая часть плоскости отвечает внутренней области угла, а какая — внешней.

Любую из двух частей, на которые развернутый угол разделяет плоскость, можно считать внутренней областью развернутого угла.

Определение внутренней области угла приводит нас ко второму определению угла.

Определение.

Угол – это геометрическая фигура, которую составляют два несовпадающих луча с общим началом и соответствующая внутренняя область угла.

Следует отметить, что второе определение угла строже первого, так как содержит больше условий. Однако не следует отметать первое определение угла, также не следует рассматривать первое и второе определения угла по отдельности. Поясним этот момент. Когда речь идет об угле как о геометрической фигуре, то под углом понимается фигура, составленная двумя лучами с общим началом. Если же возникает необходимость провести какие-либо действия с этим углом (например, измерение угла), то под углом уже следует понимать два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличия как внутренней так и внешней области угла).

Дадим еще определения смежных и вертикальных углов.

Определение.

Смежные углы – это два угла, у которых одна сторона общая, а две другие образуют развернутый угол.

Из определения следует, что смежные углы дополняют друг друга до развернутого угла.

Определение.

Вертикальные углы – это два угла, у которых стороны одного угла являются продолжениями сторон другого.

На рисунке изображены вертикальные углы.

Очевидно, что две пересекающиеся прямые образуют четыре пары смежных углов и две пары вертикальных углов.

Шкалы транпортира

Транспортир KWB имеет две шкалы — основную и вспомогательную.

Шкалы хоть и нанесены краской, но считываются однозначно. Правда стойкость к износу у них ограничена.

У основной шкалы четыре ряда значений. Один нанесен сверху шкалы, три снизу — видны в смотровое окошко подвижной планки. Каждый ряд используется для своего метода измерения углов. Каждый метод опишем подробно ниже.

Цена делений основной шкалы — один градус.

Вспомогательная шкала на подвижной планке размечена под измерение долей градуса. Цена делений — 10′ (десять минут). То есть можно измерять углы с точностью до десяти минут или до 1/6 градуса (в десятичной системе).

Список источников

• yserogo.ru
• ru.wikihow.com
• interneturok.ru
• gvozdoder.com
• edufuture.biz
• urok.1sept.ru

Как измерить угол

Для измерения углов используется транспортир:

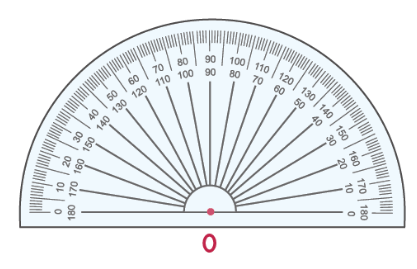
Транспортир

Попробуем измерить угол

Шаги для измерения угла .

Шаг 1: совместите транспортир с лучом OB, как показано ниже. Начните чтение с отметки 0 ° в правом нижнем углу транспортира.

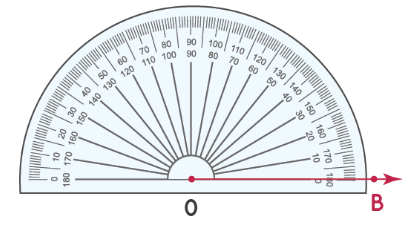
Шаг 2: Число на транспортире, совпадающее со вторым лучом, является мерой угла. Измерьте угол, используя число на «нижней дуге» транспортира. Таким образом, ∠ AOB = 37°

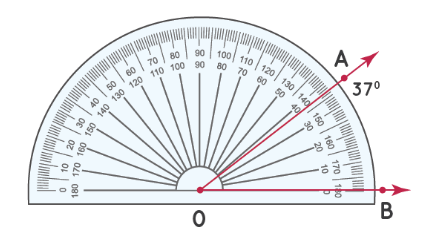
Далее попробуем измерить этот ∠AOC:

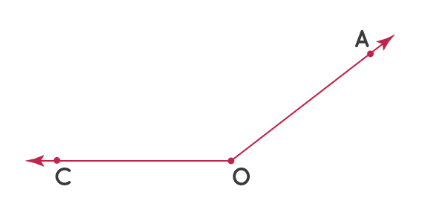
Шаг 1: Измерьте угол от отметки 0° в левом нижнем углу.

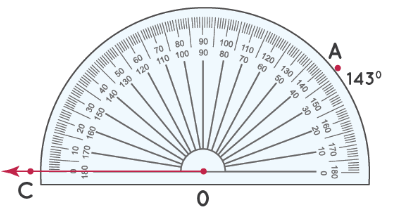
Шаг 2: Число на «верхней дуге» транспортира, совпадающее с OA, является мерой ∠ AOC. Таким образом, ∠ AOC = 143°

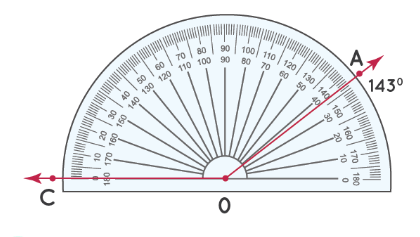
Как разметить прямой угол рулеткой

Разметка может основываться как на общей теореме Пифагора, так и на принципе “египетского треугольника”. Однако
это только в теории линии просто чертятся на бумаге, “ловить” же все выбранные размеры растянутыми шнурами или
линиями на полу – задача посложнее.

Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся
последовательность разметки изображена на картинках ниже

Важно не забывать: диагональ 141,4 см. нужно умножать на
количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах.
Картинки увеличиваются по клику!

Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах.
Картинки увеличиваются по клику!

Обозначение углов на чертеже

Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда удается правильно изобразить и обозначить тот или иной угол, дугу или название. Равные углы обозначаются как одинаковое количество дуг, а неравные как разные. На чертеже показано правильное обозначение острых, равных и неравных углов.

Когда необходимо разметить более 3-х углов, применяют специальные обозначения дуг, например, волнистые или зубчатые

Это не так важно. Ниже на картинке показано их обозначение

Обозначение угла должно быть простым, чтобы не мешать другим значениям. При решении задачи рекомендуется выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.

Углы образованные при пересечении двух прямых

При пересечении двух прямых образуются два вида углов:

• смежные;
• вертикальные.

Смежные углы

Определение

Два угла называются смежными, если они имеют общую вершину и одну общую сторону, а две другие стороны расположены на одной прямой и образуют развернутый угол. Смежные углы между собой дополняемые, так как являются продолжением один другого.

Свойства смежных углов

1. Сумма смежных углов равна 180°
2. Если оба смежных угла равны между собой, то они являются прямыми.
3. В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.
4. Синусы смежных углов равны.
5. Косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположный знак.

Вертикальные углы

Определение

Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.

Свойство: вертикальные углы равны.

Пример:

Пары углов 1 и 3; 2 и 4 – являются вертикальными

По свойству вертикальных углов:

Пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1 — являются смежными

По свойству смежных углов:

Смежные углы	Вертикальные углы
Два угла с общей стороной и вершиной называются смежными.	Когда две прямые пересекаются друг с другом, то пары противоположных углов, образованных при вершине, называются вертикальными углами.
Имеют общую сторону и общую вершину.	Имеют общую вершину, но не имеют общую сторону
Смежные углы не всегда равны по величине	Вертикально противоположные углы равны по величине

Разница между смежными и вертикальными углами

Что такое угол?

Угол – это фигура, состоящая из двух лучей, имеющих начало в одной точке. Эта точка зовется вершиной угла. Величина угла показывает величину поворота оной стороны относительно другой. Наиболее ярким примером станут часы.

На сколько поворачивается минутная стрелка относительно другой? На какое-то количество минут. Так и геометрии, один луч поворачивается вокруг другого на какое-то количество градусов.

Изучение углов необходимо в физике, где колесо вращается вокруг оси; в строительстве, где у каждого строительного элемента есть вращательный момент и во многих других отраслях науки.

Углы есть практически во всех фигурах. Только круг без дополнительных построений не имеет в своем составе углов. Но стоит только провести радиус и углы сразу же появляются

Без углов нельзя себе представить треугольник, прямоугольник и прочие многоугольники. Это один из основных элементов геометрических фигур.

Углы существуют не только в плоскости, но и в пространстве. При пересечении двух плоскостей по прямой так же, как и при пересечении прямых образуется четыре угла. Чтобы найти величину такого угла придется построить плоский угол. Для этого необходимо в каждой плоскости провести перпендикуляр к одной точке, лежащей на линии пересечения плоскостей.

Угол между двумя перпендикулярами и будет равняться пространственному углу

Обратите внимание, угол между перпендикулярами в пространстве не всегда равняется 90 градусам

Определение

Для начала, нужно рассмотреть просто меру угла. В этом поможет изображение луча и прямой линии. Сначала нужно провести, например, горизонтальную прямую линию. Затем от её первой точки проводится луч, не параллельный прямой. Таким образом, между прямой и лучом появляется некоторое расстояние, небольшой угол. Мера угла – это размер этого самого поворота луча.

Это понятие обозначает определенное цифровое значение, которое будет больше нуля. Оно выражается в градусах, а также его составных частях, то есть минутах и секундах. То количество градусов, которое поместится в угол между лучом и прямой, и будет градусной мерой.