Таблица синусов

Тангенс

Отношение (см. рис. 161) называется тангенсом угла и обозначается символом tg . Итак, tg = .

Отношение для угла, близкого к нулю, т. е. тангенс угла, близкого к нулю, является числом, близким к нулю. Например, tg 2° = 0,035; tg 1° = 0,017.

Если угол близок к 90°, но меньше, чем 90°, то его тангенс будет положительным числом, которое тем больше, чем ближе угол к 90°.

Когда радиус-вектор окажется расположенным в четверти I, то и ордината у и абсцисса x будут положительными, а потому будет положительным и отношение , т. е. tg .

Если радиус-вектор окажется в четверти II, то tg < 0.Для четверти III tg > 0 и для четверти IV tg < 0.

Если угол близок к 90°, но больше, чем 90°, то отношение , т. е. tg , будет числом отрицательным, которое по своей абсолютной величине тем больше, чем ближе угол к 90°.

Изменение тангенса. Изменения тангенса даны на следующей таблице:

Читается так: если угол возрастает от 0 до 90°, то tg возрастает от нуля до плюс бесконечности; если угол возрастает от 90 до 180° , то tg возрастает от минус бесконечности до нуля и т. д.

Процесс изменения tg повторяется после каждого пол-оборота радиуса-вектора . Поэтому

tg(180° n + ) = tga,

где n — любое целое число.

Обратим внимание на то, что tg 0° = tg 180° = tg 360° = =tg (—180°)== tg (— 360°)=0. Тангенс угла 90° не существует, так как при = 90° абсцисса x обращается в нуль и отношение теряет смысл

По такой же причине не существует и тангенса угла 270°.

Наряду с этим принято писать, что (читается так: тангенс угла 90° равен плюс или минус бесконечности).

Также

Мы сказали, что tg 90° не существует и что . Но в этих двух утверждениях нет противоречия. Когда мы говорим, что тангенс равен бесконечности, то это и значит, что он не существует.

Запись характеризует картину изменения тангенса вблизи угла 90° слева и справа от него. Когда угол приближается к 90°, оставаясь меньше 90°, тангенс принимает положительные неограниченно возрастающие значения. Когда же угол , приближаясь к 90°, остается больше 90°, то тангенс принимает отрицательные значения, также неограниченно возрастающие по своей абсолютной величине.

Каждому значению , взятому на промежутке (0°; 90°) или (90°; 180°) и т. д., соответствует единственное определенное значение tg, т. е. tg есть на каждом из указанных промежутков однозначная функция аргумента .

Значения функции tg есть числа отвлеченные.

С изменением угла изменяется и tg . Однако могут быть случаи, когда неодинаковые углы имеют одинаковые тангенсы. Например, tg 225° = tg 45° = 1.

Функция tg, изменяясь, может принимать любое действительное значение.

Тангенс острого угла прямоугольного треугольника. В прямоугольном треугольника ОМР (см. рис. 161) с острым углом отрезок MP есть катет, противолежащий углу , а ОР прилежащий. Поэтому тангенс острого угла прямоугольного треугольника есть отношение противолежащего катета к прилежащему.

Возьмем прямоугольный треугольник с катетами a и b, гипотенузой с и острыми углами и (рис. 163); тогда

Замечание:

Функции sin, cos , tg возникли исторически из таких задач, в которых надо было находить одни элементы треугольника в зависимости от других. Поэтому эти функции получили название тригонометрических функций. Слово «тригонометрия» составлено из греческих слов: «тригоном» — треугольник и «метрезис» — измерение. Но тригонометрические функции оказались необычайно мощным средством для решения не только геометрических вопросов, а но и многочисленных весьма важных вопросов математического анализа, естествознания и техники.

Замечание:

Знак sin называется не синусом, а лишь знаком синуса и сам по себе никакой величины не изображает. Он является знаком нового математического действия. Это относится и к знакам cos или tg.

Значения всех тригонометрических функций суть числа отвлеченные.

Замечание:

Выражение надо понимать как . Например,

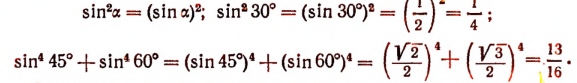
Сказанное распространяется и на остальные тригонометрические функции.

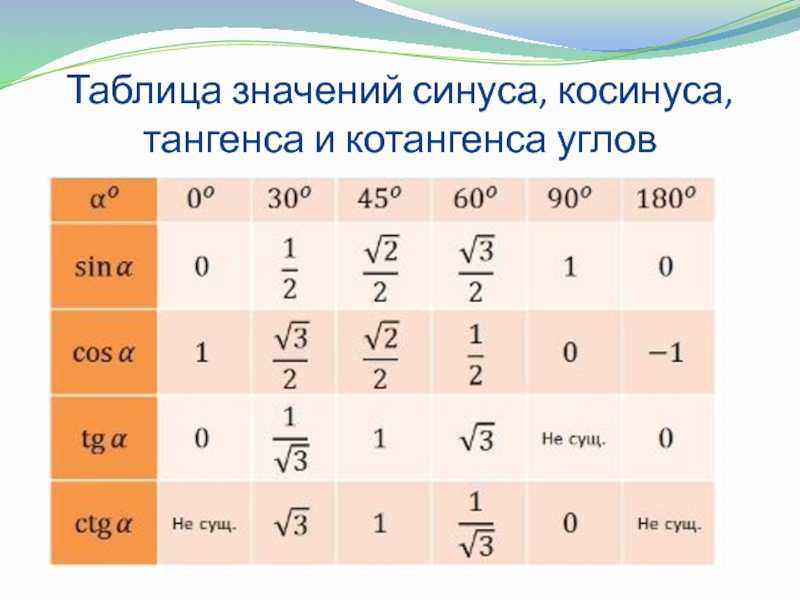
Использование таблицы

В таблице достаточно найти необходимую тригонометрическую функцию и значение угла или радиан, для которых эту функцию нужно вычислить. На пересечении строки с функцией и столбца со значением получим искомое значение тригонометрической функции заданного аргумента.

На рисунке можно увидеть, как найти значение $\cos⁡60°$, которое равно $\frac{1}{2}$.

Аналогично используется расширенная тригонометрическая таблица. Преимуществом ее использования является, как уже упоминалось, вычисление тригонометрической функции практически любого угла. Например, легко можно найти значение $\tan 1 380°=\tan (1 380°-360°)=\tan(1 020°-360°)=\tan(660°-360°)=\tan300°$:

Таблица синусов углов от 181° до 360°

sin(181°) = -0.017452sin(182°) = -0.034899sin(183°) = -0.052336sin(184°) = -0.069756sin(185°) = -0.087156sin(186°) = -0.104528sin(187°) = -0.121869sin(188°) = -0.139173sin(189°) = -0.156434sin(190°) = -0.173648sin(191°) = -0.190809sin(192°) = -0.207912sin(193°) = -0.224951sin(194°) = -0.241922sin(195°) = -0.258819sin(196°) = -0.275637sin(197°) = -0.292372sin(198°) = -0.309017sin(199°) = -0.325568sin(200°) = -0.34202sin(201°) = -0.358368sin(202°) = -0.374607sin(203°) = -0.390731sin(204°) = -0.406737sin(205°) = -0.422618sin(206°) = -0.438371sin(207°) = -0.45399sin(208°) = -0.469472sin(209°) = -0.48481sin(210°) = -0.5sin(211°) = -0.515038sin(212°) = -0.529919sin(213°) = -0.544639sin(214°) = -0.559193sin(215°) = -0.573576sin(216°) = -0.587785sin(217°) = -0.601815sin(218°) = -0.615661sin(219°) = -0.62932sin(220°) = -0.642788sin(221°) = -0.656059sin(222°) = -0.669131sin(223°) = -0.681998sin(224°) = -0.694658sin(225°) = -0.707107

sin(226°) = -0.71934sin(227°) = -0.731354sin(228°) = -0.743145sin(229°) = -0.75471sin(230°) = -0.766044sin(231°) = -0.777146sin(232°) = -0.788011sin(233°) = -0.798636sin(234°) = -0.809017sin(235°) = -0.819152sin(236°) = -0.829038sin(237°) = -0.838671sin(238°) = -0.848048sin(239°) = -0.857167sin(240°) = -0.866025sin(241°) = -0.87462sin(242°) = -0.882948sin(243°) = -0.891007sin(244°) = -0.898794sin(245°) = -0.906308sin(246°) = -0.913545sin(247°) = -0.920505sin(248°) = -0.927184sin(249°) = -0.93358sin(250°) = -0.939693sin(251°) = -0.945519sin(252°) = -0.951057sin(253°) = -0.956305sin(254°) = -0.961262sin(255°) = -0.965926sin(256°) = -0.970296sin(257°) = -0.97437sin(258°) = -0.978148sin(259°) = -0.981627sin(260°) = -0.984808sin(261°) = -0.987688sin(262°) = -0.990268sin(263°) = -0.992546sin(264°) = -0.994522sin(265°) = -0.996195sin(266°) = -0.997564sin(267°) = -0.99863sin(268°) = -0.999391sin(269°) = -0.999848sin(270°) = -1

sin(271°) = -0.999848sin(272°) = -0.999391sin(273°) = -0.99863sin(274°) = -0.997564sin(275°) = -0.996195sin(276°) = -0.994522sin(277°) = -0.992546sin(278°) = -0.990268sin(279°) = -0.987688sin(280°) = -0.984808sin(281°) = -0.981627sin(282°) = -0.978148sin(283°) = -0.97437sin(284°) = -0.970296sin(285°) = -0.965926sin(286°) = -0.961262sin(287°) = -0.956305sin(288°) = -0.951057sin(289°) = -0.945519sin(290°) = -0.939693sin(291°) = -0.93358sin(292°) = -0.927184sin(293°) = -0.920505sin(294°) = -0.913545sin(295°) = -0.906308sin(296°) = -0.898794sin(297°) = -0.891007sin(298°) = -0.882948sin(299°) = -0.87462sin(300°) = -0.866025sin(301°) = -0.857167sin(302°) = -0.848048sin(303°) = -0.838671sin(304°) = -0.829038sin(305°) = -0.819152sin(306°) = -0.809017sin(307°) = -0.798636sin(308°) = -0.788011sin(309°) = -0.777146sin(310°) = -0.766044sin(311°) = -0.75471sin(312°) = -0.743145sin(313°) = -0.731354sin(314°) = -0.71934sin(315°) = -0.707107

sin(316°) = -0.694658sin(317°) = -0.681998sin(318°) = -0.669131sin(319°) = -0.656059sin(320°) = -0.642788sin(321°) = -0.62932sin(322°) = -0.615661sin(323°) = -0.601815sin(324°) = -0.587785sin(325°) = -0.573576sin(326°) = -0.559193sin(327°) = -0.544639sin(328°) = -0.529919sin(329°) = -0.515038sin(330°) = -0.5sin(331°) = -0.48481sin(332°) = -0.469472sin(333°) = -0.45399sin(334°) = -0.438371sin(335°) = -0.422618sin(336°) = -0.406737sin(337°) = -0.390731sin(338°) = -0.374607sin(339°) = -0.358368sin(340°) = -0.34202sin(341°) = -0.325568sin(342°) = -0.309017sin(343°) = -0.292372sin(344°) = -0.275637sin(345°) = -0.258819sin(346°) = -0.241922sin(347°) = -0.224951sin(348°) = -0.207912sin(349°) = -0.190809sin(350°) = -0.173648sin(351°) = -0.156434sin(352°) = -0.139173sin(353°) = -0.121869sin(354°) = -0.104528sin(355°) = -0.087156sin(356°) = -0.069756sin(357°) = -0.052336sin(358°) = -0.034899sin(359°) = -0.017452sin(360°) = 0

Тригонометрия в прямоугольном треугольнике

https://youtube.com/watch?v=O9dutltOPuw%3Ffeature%3Doembed%26iv_load_policy%3D3%26modestbranding%3D1%26rel%3D0%26autohide%3D1%26playsinline%3D0%26autoplay%3D0

Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

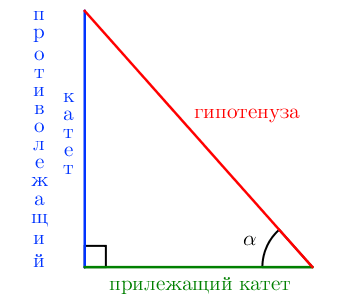
Синус угла – отношение противолежащего катета к гипотенузе.

sin α = Противолежащий катет гипотенуза

Косинус угла – отношение прилежащего катета к гипотенузе.

cos α = Прилежащий катет гипотенуза

Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).

tg α = Противолежащий катет Прилежащий катет

Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).

ctg α = Прилежащий катет Противолежащий катет

https://youtube.com/watch?v=zON3wQijyxg%3Ffeature%3Doembed%26iv_load_policy%3D3%26modestbranding%3D1%26rel%3D0%26autohide%3D1%26playsinline%3D0%26autoplay%3D0

Рассмотрим прямоугольный треугольник ABC, угол C равен 90°:

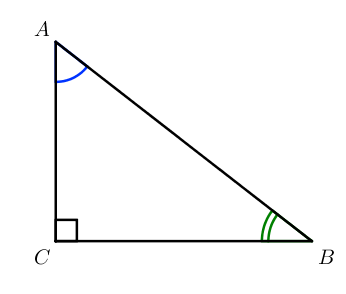
sin ∠ A = C B A B

cos ∠ A = A C A B

tg ∠ A = sin ∠ A cos ∠ A = C B A C

ctg ∠ A = cos ∠ A sin ∠ A = A C C B

sin ∠ B = A C A B

cos ∠ B = B C A B

tg ∠ B = sin ∠ B cos ∠ B = A C C B

ctg ∠ B = cos ∠ B sin ∠ B = C B A C

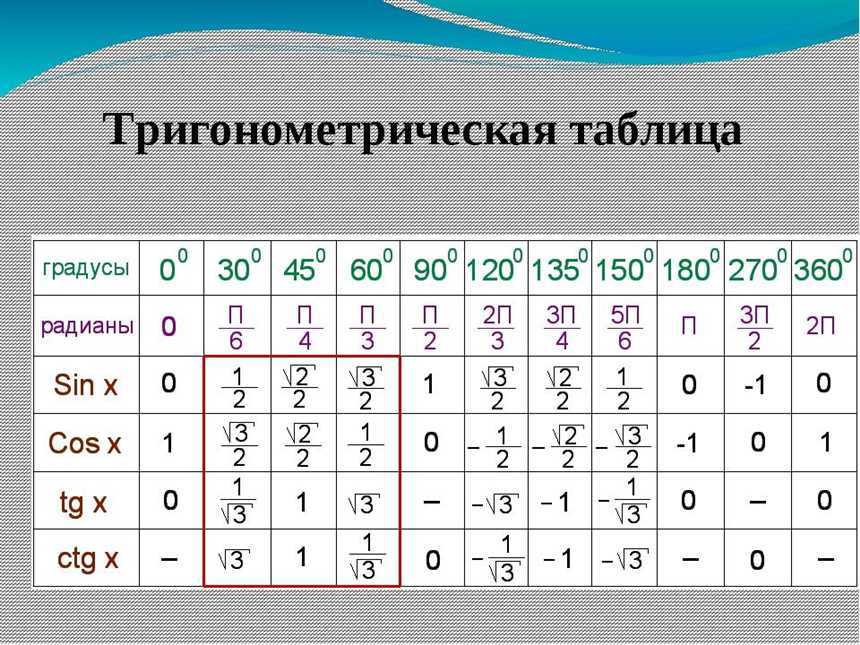
Градусы углов

Градусная мера угла и наиболее распространенными единицами измерения угла являются градус и радиан. Один градус — это $\frac$ полного круга. $90$ градусов — это четверть круга, $180$ – половина круга (это то, сколько градусов развернутый угол), $270$ — три четверти круга (это то, сколько градусов тупой угол) и $360$ это целый круг.

Прямой угол равен $90$ градусов, острый угол больше $0$ и меньше $90$ градусов и тупой угол больше $90$ градусов и меньше $180$ градусов. Развернутый угол равен $180$ градусам.

Мы изучаем углы от $0$ ° до $360$ °, но есть углы больше $360$ ° и отрицательные углы.

Градусы могут быть разделены на минуты и секунды. Каждый градус делится на $60$ равных частей, которые называются минутами. Так семь с половиной градусов можно сказать $7$ градусов и $30$ минут и записать $7$ ° $30$ ‘. Каждая минута делится на $60$ равных частей, каждая из которых равна одной секунде. Например, $2$ градуса $5$ минут $30$ секунд записывается $2$ ° $5$ ‘ $30$ «. Деление градуса на минуты и секунды аналогично делению часа на минуты и секунды времени.

Виды углов Острые углы: углы, чья мера меньше 90 градусов. Прямые углы: углы, чья мера равна 90 градусов. Тупые углы: углы, чья мера больше 90 градусов. Равные углы: углы, чьи меры совпадают. Смежные углы: два угла, которые имеют общую вершину и общую сторону, но не пересекаются внутри этой стороны. Вертикальные углы: два угла, чьи стороны являются противоположными лучами пересекающихся прямых. Вертикальные углы равны между собой. Смежно-вертикальные углы: два угла, один из которых является вертикальным углом, а другой — смежным с ним углом. Смежно-вертикальные углы равны между собой.

Угол — это геометрическая фигура, которая образуется двумя лучами, исходящими из общей начальной точки. Начальная точка угла называется вершиной, а лучи — сторонами угла. Измеряется в градусах или радианах.

Таблица синусов для 181°-360°

Если страница помогла, сохраните её и поделитесь ссылкой с друзьями.

10.02.2018 21:16:21

2018-02-10 21:16:21

Любые данныеЛюбые данные Любые данные Любые данные

Определение Sin Cos Tan

Прежде чем вводить таблицу тригонометрических значений, рекомендуется сначала понять термины тригонометрия и sin cos tan.

Тригонометрия — это раздел математики, изучающий взаимосвязь между длиной и углом треугольника.
Sin (синус) — это отношение длины треугольника между передней частью угла и гипотенузой y / z.
Cos (косинус) — это отношение длины в треугольнике между стороной угла и гипотенузой, x / z.
Тан (тангенс) — это отношение длин треугольника между передней частью угла и стороной y / x.

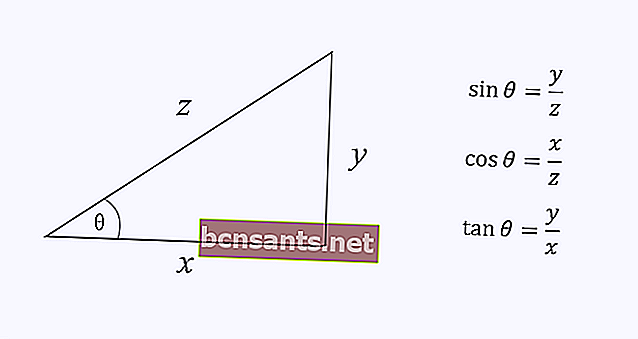
Все тригонометрические сравнения tan sin cos ограничиваются только допустимыми прямоугольными треугольниками или треугольниками с одним углом 90 градусов.

Формулы приведения

https://youtube.com/watch?v=ZXnwaY6ogdY%3Ffeature%3Doembed%26iv_load_policy%3D3%26modestbranding%3D1%26rel%3D0%26autohide%3D1%26playsinline%3D0%26autoplay%3D0

Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,

можно заметить, что:

sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °

sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °

sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °

sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °

cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °

cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °

cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °

cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °

Рассмотрим тупой угол β:

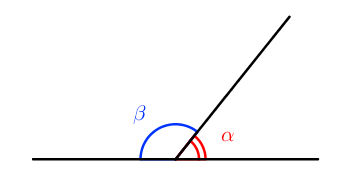
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:

sin ( 180 ° − α ) = sin α

cos ( 180 ° − α ) = − cos α

tg ( 180 ° − α ) = − tg α

ctg ( 180 ° − α ) = − ctg α

Таблицы тригонометрических функций

−1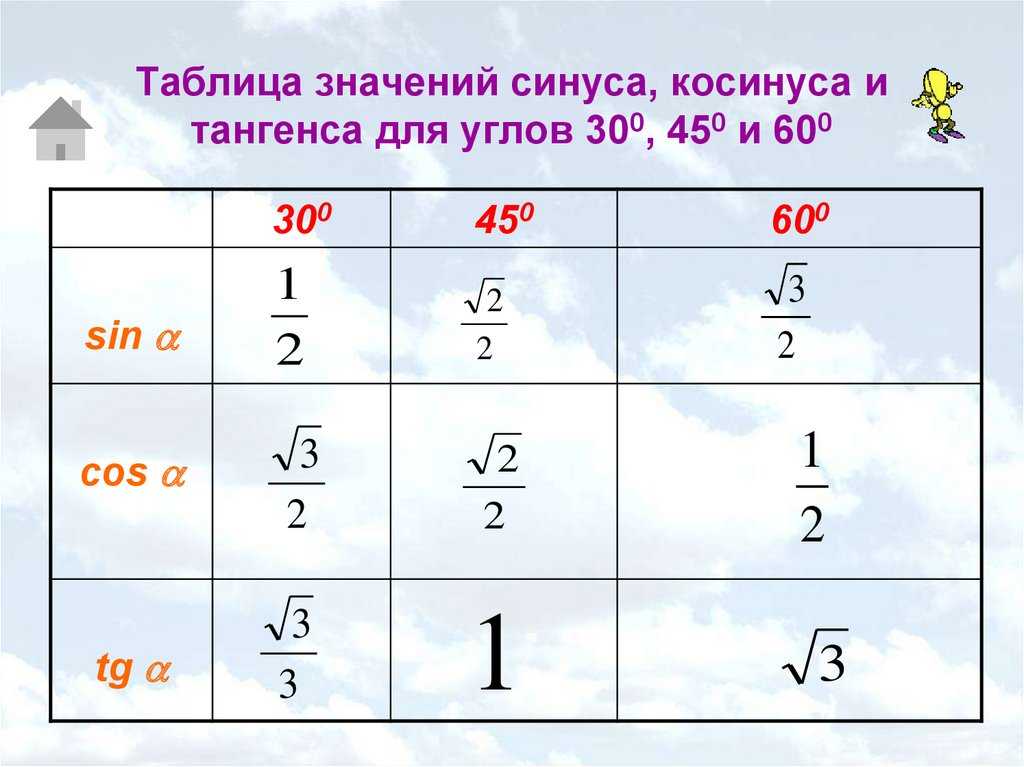

Пример 1: Чему равен синус 48°?

Пример 2: Косинус какого угла равен 0,3912?

Хотя калькулятор может легко найти тригонометрические функции дробной меры угла, это может быть неверно, если для поиска значений необходимо использовать таблицу. Таблицы не могут перечислить всех углов. Поэтому для нахождения значений между значениями, перечисленными в таблице, необходимо использовать аппроксимацию. Этот метод известен как линейная интерполяция . Сделано предположение, что различия в значениях функций прямо пропорциональны различиям мер углов на малых интервалах .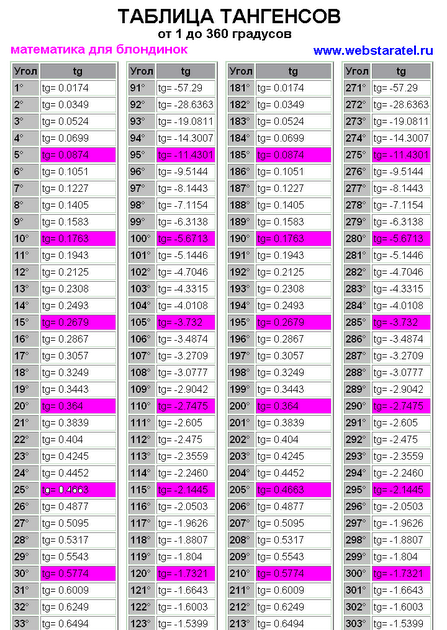

Пример 3 С помощью линейной интерполяции найдите тангенс 28,43°, учитывая, что тангенс 28,40° = 0,5407 и тангенс 28,50° = 0,5430.

Установите пропорцию, используя переменную x .

Поскольку x — это разница между тангенсом 28,40° и тангенсом 28,43°,

Пример 4: Найдите первый квадрант угла α, где cos α ≈ 0,2622, учитывая, что cos 74° ≈ 0,275 и стоимость 75° ≈ 0,2588.

Установите пропорцию, используя переменную x .

Следовательно, α ≈ 74,0° + 0,8° ≈ 74,8°

Существует интересный метод аппроксимации для нахождения синуса и тангенса углов, меньших 0,4 радиана (примерно 23°). Синус и тангенс углов менее 0,4 радиана примерно равны угловой мере. Например, в радианах sin0,15 ≈ 0,149.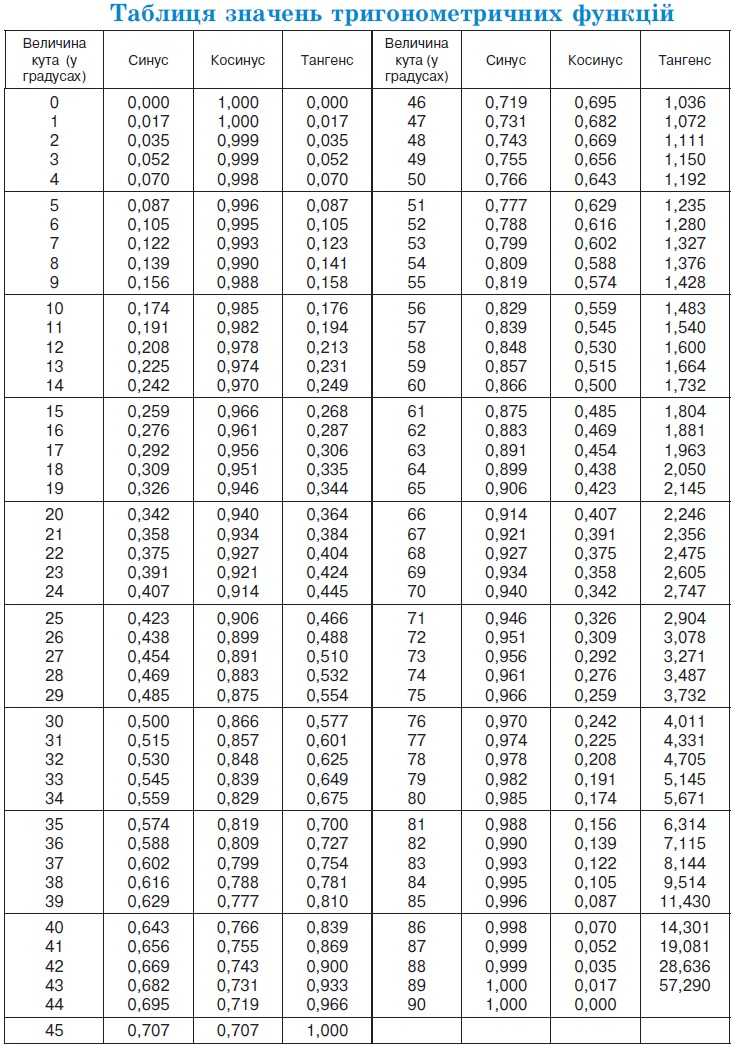

Тригонометрические уравнения

Это тема 10-11 классов.

Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!

https://youtube.com/watch?v=qOkSr14uWAI%3Ffeature%3Doembed%26iv_load_policy%3D3%26modestbranding%3D1%26rel%3D0%26autohide%3D1%26playsinline%3D0%26autoplay%3D0

https://youtube.com/watch?v=VsQLfKTZSYc%3Ffeature%3Doembed%26iv_load_policy%3D3%26modestbranding%3D1%26rel%3D0%26autohide%3D1%26playsinline%3D0%26autoplay%3D0

https://youtube.com/watch?v=L6tmUnxcGIE%3Ffeature%3Doembed%26iv_load_policy%3D3%26modestbranding%3D1%26rel%3D0%26autohide%3D1%26playsinline%3D0%26autoplay%3D0

https://youtube.com/watch?v=TwTqTS2-u64%3Ffeature%3Doembed%26iv_load_policy%3D3%26modestbranding%3D1%26rel%3D0%26autohide%3D1%26playsinline%3D0%26autoplay%3D0

График синуса и косинуса

Заметим, что координаты точек, лежащей на единичной окружности, варьируются в пределах от – 1 до 1. Это означает, что значение синуса и косинуса также может находиться только в интервале между этими числами. Получается, что область значения этих ф-ций – это промежуток .

Вычислить синус и косинус можно для абсолютно любого угла поворота, поэтому область определения этих тригонометрических ф-ций – вся числовая прямая, то есть промежуток (– ∞; + ∞).

Изучение графиков тригонометрических функций начнем с синуса. В тригонометрии при построении графика синуса принято по оси Ох откладывать значение угла в радианах, а не в градусах. Из-за этого в школьной тетради тяжело точно отметить точки, через которые проходит этот график. Например, возьмем угол, равный 90°. Его величина в радианах π/2, а sinπ/2 = 1. Получается, график должен пройти через точку (π/2; 1). Однако число π/2 – иррациональное, равное примерно 1,5708…, и точно отложить отрезок длиной π/2 невозможно.

Поэтому в учебных целях график строят приближенно (естественно, что на практике точный график можно построить с помощью компьютера с любой требуемой точностью). Считают, что величина π/2 примерно равна 1,5, то есть дроби 3/2. Если выбрать масштаб, при котором единице равны 2 клеточки, то π/2 – это 3 клеточки. Тогда π/6 – это одна клеточка, а π/3 – две.

Мы знаем, что

sin 0 = 0

sin π/6 = 1/2

sin π/2 = 1

Значит, график синуса должен проходить через точки (0; 0), (π/6; 1/2) и (π/2; 1). Отметим их на координатной плоскости:

С помощью некоторых соображений симметрии можно вычислить ещё несколько точек в диапазоне от 0 до 2π. Не будем перечислять их координаты, а просто отметим их на рисунке:

Теперь соединим их плавной кривой:

Мы получили график синуса на промежутке от 0 до 2π. Но ведь мы можем вычислить синус для любого другого угла! При этом мы используем тот факт, что углам, отличающимся на 2π (на один полный оборот), на единичной окружности соответствует одинаковая точка. То есть этим двум углам будут соответствовать точки на графике с одинаковой ординатой (координатой у), но абсциссами, отличающимися на 2π. Другими словами, точку графика можно перенести на 2π (то есть 12 клеточек) влево или вправо:

Перенести можно не одну точку, а сразу всё множество точек, лежащих между 0 и 2π:

Получили ещё два участка графика, на промежутках и . Эти участки также можно переместить влево и вправо. Продолжая этот процесс бесконечно, мы получим весь график у = sinx:

В результате мы получили кривую, которую называют синусоидой.

Теперь построим график косинуса. Мы знаем что

cos 0 = 1

cos π/3 = 1/2

cos π/2 = 1

Получается, что график должен проходить через точки (0;1), (π/3; 1/2) и (π/2; 0). Отметим их на плоскости:

Можно вычислить, используя симметрию на единичной окружности, ещё несколько точек, которые должны лежать на графике. Не приводя этих вычислений, просто отметим эти точки на плоскости:

Соединяем эти точки плавной линией:

Как и в случае с синусом, участок графика косинуса можно перенести на 2π (12 клеточек влево и вправо). В результате таких действий получим окончательный вид ф-ции у = cosх:

Можно заметить несколько особенностей полученных графиков. Во-первых, все точки обоих графиков лежат в «полосе» между прямыми у = 1 и у = – 1. Это следствие того, что и у синуса, и у косинуса область значений – это промежуток :

Во-вторых, график косинуса очень похож на синусоиду. Он имеет такую же форму, но просто смещен на π/2 (3 клеточки) влево. Это не случайно, в будущих уроках мы узнаем причину этого явления. Но, так как график косинуса – это просто смещенная синусоида, то термин «косинусоида» для его обозначения почти не используется – он просто избыточен.

В-третьих, графики обладают периодичностью. Они «повторяются» с периодом 2π. Дело в том, что углам, отличающимся друг от друга на 2π (то есть ровно на один полный поворот в 360°), на единичной окружности соответствует одна и та же точка. То есть справедливы формулы:

sin (x+ 2π) = sinx

cos (x+ 2π) = sinx

В-четвертых, можно заметить, что график косинуса симметричен относительно оси Ох, а график синуса симметричен относительно начала координат. Это значит, что синус является , а косинус – . Напомним, что ф-ция f(x) является нечетной, если справедливо условие

f(x) = – f(– x)

Если f(x) – четная ф-ция, то должно выполняться условие:

f(x) = f(– x)

Действительно, если отложить на единичной окружности углы α и (– α), то можно заметить, что их косинусы будут равны друг другу, и синусы окажутся противоположными:

Поэтому верны формулы:

sin (– α) = – sinα

cos (– α) = cosα

Использование таблицы

На рисунке можно увидеть, как найти значение $\cos⁡60°$, которое равно $\frac{1}{2}$.

Сколько градусов составляет прямой угол?

Мы изучаем углы от $0$ ° до $360$ °, но есть углы больше $360$ ° и отрицательные углы.

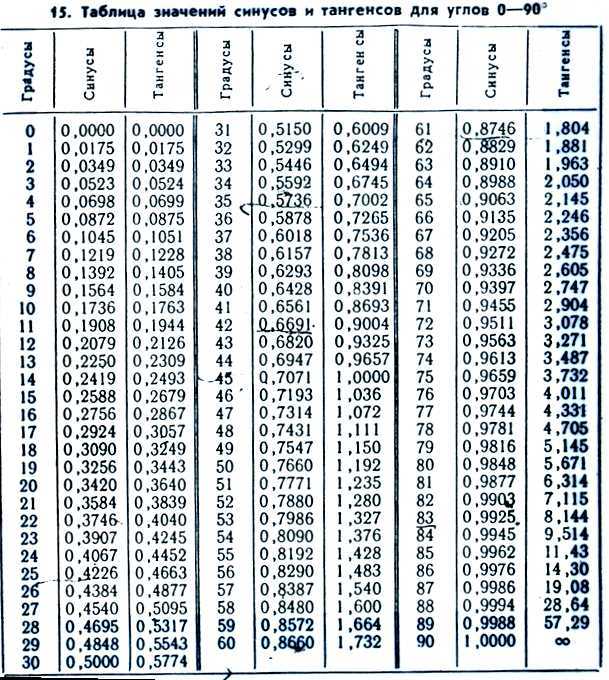
Синусы углов: как легко до них добраться?

Синус угла — это функция, которая выражает отношение противоположной стороны треугольника к его гипотенузе. Синус угла можно выразить в градусах или радианах, но в данной статье мы сосредоточимся на градусах. Зная значения синусов основных углов, мы можем легко вычислить синус любого другого угла.

Периодичность и запоминание значений синусов углов

Значения синусов углов имеют периодичность, повторяясь с определенным шагом. Запомнить значения синусов углов от 0° до 180° можно с помощью таблицы:

Угол (градусы)	Значение синуса
0°
30°	0.5
45°	0.707
60°	0.866
90°	1
180°

Также для удобства запоминания можно использовать вариант: «получай 0, получай 1 и корень из двух под наклоном». Эта фраза поможет вам быстро вспомнить значения синусов для основных углов.

Значения синусов углов от 0° до 360°

Если в таблице представлены значения синусов углов от 0° до 180°, как же узнать значения синусов для углов от 180° до 360°? Для этого можно использовать следующую таблицу:

Угол (градусы)	Значение синуса
180°
210°	-0.5
225°	-0.707
240°	-0.866
270°	-1
360°

Теперь для углов от 180° до 360° можно использовать полученные значения синусов.

Применение значений синусов углов

Зная значения синусов углов, мы можем их использовать в различных областях. Например:

При решении задач физики, где необходимо учесть силу трения, давление в жидкостях и другие физические явления;
При вычислении координат точек на графике;
При моделировании и анализе процессов в инженерном дизайне;
В тригонометрии для решения уравнений и построения графиков.

Используйте таблицу синусов углов для упрощения вычислений и решения различных задач!

Тангенс

Использование таблицы

Таблица синусов углов от 181° до 360°

Тригонометрия в прямоугольном треугольнике

Градусы углов

Определение Sin Cos Tan

Формулы приведения

Таблицы тригонометрических функций

Тригонометрические уравнения

График синуса и косинуса

Использование таблицы

Сколько градусов составляет прямой угол?

Синусы углов: как легко до них добраться?

Периодичность и запоминание значений синусов углов

Значения синусов углов от 0° до 360°

Применение значений синусов углов

Похожие записи:

Похожие записи: