Формулы приведения. как быстро получить любую формулу приведения

Тригонометрия и тригонометрические функции

Тригонометрия – раздел математики, изучающий зависимости углов и сторон треугольников, которые выражены функциями, называемыми тригонометрическими.

Функция – это правило, описывающее зависимость одной величины от другой.

Угол – это геометрическая фигура, образованная двумя линиями, не лежащими на одной прямой и выходящими или пересекающимися в одной точке.

Углы по своему виду могут быть:

Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки называют сторонами треугольника, а точки – вершинами треугольника.

В зависимости от соотношения сторон и углов, треугольники можно разделить на группы:

• По величине угла:
• прямоугольный
• тупоугольный
• остроугольный

• По длине сторон:
• равносторонний
• разносторонний
• равнобедренный

Таблица основных тригонометрических функций для углов 0, 30, 45, 60, 90, …, 360 градусов

Исходя из определений синуса, косинуса, тангенса и котангенса можно найти значения этих функций для углов 0 и 90 градусов

sin 0=0, cos 0=1, tg 0=0, котангенс нуля – не определен,

sin 90°=1, cos 90°=0, сtg 90°=0, тангенс дявяноста градусов не определен.

Значения синусов, косинусов, тангенсов и котангенсов в курсе геометрии определяются как соотношения сторон прямоугольного треугольника, углы которого равны 30, 60 и 90 градусов, и также 45, 45 и 90 градусов.

Определение тригонометрических функуций для острого угла в прямоугольном треугольнике

Синус – отношение противолежащего катета к гипотенузе.

Косинус – отношение прилежащего катета к гипотенузе.

Тангенс – отношение противолежащего катета к прилежащему.

Котангенс – отношение прилежащего катета к противолежащему.

В соответствии с определениями находятся значения функций:

sin 30°=12, cos 30°=32, tg 30°=33, ctg 30°=3,sin 45°=22, cos 45°=22, tg 45°=1, ctg 45°=1,sin 60°=32, cos 45°=12, tg 45°=3, ctg 45°=33.

Сведем эти значения в таблицу и назовем ее таблицей основных значений синуса, косинуса, тангенса и котангенса.

Таблица основных значений синусов, косинусов, тангенсов и котангенсов

α°030456090sin α01222321cos α13222120tg α03313не определенctg αне определен31330α, радиан0π6π4π3π2

Одно из важных свойств тригонометрических функций – периодичность. На основе этого свойства данную таблицу можно расширить,используя формулы приведения. Ниже представим расширенную таблицу значений основных тригонометрических функций для углов 0, 30, 60, … ,120, 135, 150, 180, … , 360 градусов ( 0 ,   π 6 ,   π 3 ,   π 2 ,   . . .   ,   2 π радиан).

Таблица синусов, косинусов, тангенсов и котангенсов

α°030456090120135150180210225240270300315330360sin α012223213222120-12-22-32-1-32-22-120cos α13222120-12-22-32-1-32-22-1201222321tg α03313–1-33003313–3-1 0ctg α-31330-33-1-3-31330-33-1-3-α, радиан0π6π4π3π22π33π45π6π7π65π44π33π25π37π411π62π

Периодичность синуса, косинуса, тангенса и котангенса позволяет расширять эту таблицу до сколь угодно больших значений углов. Значения, собранные в таблице, используются при решении задач чаще всего, поэтому их рекомендуется выучить наизусть.

Формулы суммы и разности для формул приведения

И я обещал еще рассказать третий способ, как пользоваться формулами приведения. Он не очень удобный, потому что придется гораздо больше считать и выучить 4 тригонометрические формулы синуса/косинуса суммы/разности:
$$\sin(\alpha\pm\beta)=\sin(\alpha)*\cos(\beta)\pm\sin(\beta)*\cos(\alpha);$$
$$\cos(\alpha\pm\beta)=\cos(\alpha)*\cos(\beta)\mp\sin(\alpha)*\sin(\beta);$$
Приведем пример использования одной из таких формул:

Пример 9
Вычислите:
$$\sin(\frac{\pi}{3}+\frac{\pi}{6})=?;$$
Перед нам формула синуса суммы, где \(\alpha=\frac{\pi}{3}\), а \(\beta=\frac{\pi}{6}\). Просто подставим значения в формулу:
$$\sin(\frac{\pi}{3}+\frac{\pi}{6})=\sin(\frac{\pi}{3})*\cos(\frac{\pi}{6})+\sin(\frac{\pi}{6})*\cos(\frac{\pi}{3});$$
Значения всех тригонометрических функций в формуле мы можем посчитать, ведь это табличные значения:
$$\sin(\frac{\pi}{3}+\frac{\pi}{6})=\sin(\frac{\pi}{3})*\cos(\frac{\pi}{6})+\sin(\frac{\pi}{6})*\cos(\frac{\pi}{3})=\frac{\sqrt{3}}{2}*\frac{\sqrt{3}}{2}+\frac{1}{2}*\frac{1}{2}=\frac{3}{4}+\frac{1}{4}=1;$$

Эти формулы, на самом деле, надо знать в любом случае, они даже встречаются на ЕГЭ. А здесь они нам помогут выводить формулы приведения.

Опять будем учиться на примерах:

Пример 10
$$\sin(\alpha+\frac{3\pi}{2})=?;$$
Посмотрите внимательно, он абсолютно ничем не отличается от примера под номером 9. Мы здесь тоже можем применить формулу синуса суммы, где \(\beta=\frac{3\pi}{2}\).
$$\sin(\alpha+\frac{3\pi}{2})=\sin(\alpha)*\cos(\frac{3\pi}{2})+\sin(\frac{3\pi}{2})*\cos(\alpha);$$
Косинус и синус от \(\frac{3\pi}{2}\) можно легко посчитать:
$$\sin(\frac{3\pi}{2})=-1;$$
$$\cos(\frac{3\pi}{2})=0;$$
И подставим в нашу формулу:
$$\sin(\alpha+\frac{3\pi}{2})=\sin(\alpha)*\cos(\frac{3\pi}{2})+\sin(\frac{3\pi}{2})*\cos(\alpha)=\sin(\alpha)*0+(-1)*\cos(\alpha)=-\cos(\alpha);$$
Мы получили, что:
$$\sin(\alpha+\frac{3\pi}{2})=-\cos(\alpha);$$
Вывели формулу приведения, используя синус суммы.
Этот способ, на мой взгляд, гораздо менее удобный, чем правило лошади, но им тоже можно пользоваться. Главное, не ошибиться в вычислениях.

Примеры использования формул приведения

Для начало отметим, что существует довольно много способов представления угла под знаком тригонометрических функций в виде:

\(\pm\alpha+2\pi\times z,\;\frac\pi2\pm\alpha+2\pi\times z\;и\;\frac{3\pi}2\pm\alpha+2\pi\times z\)

Это обусловлено тем, что угол может принимать любое значение.

Например, возьмем угол \(\frac{16\pi}3\). Его можно представить как

\(\pi+\frac\pi3+2\pi\times2\)

или

\(-\frac{2\pi}3+2\pi\times3\)

или же

\(\frac{3\pi}2-\frac\pi6+2\pi\times2\)

Далее сравним, какие формулы приведения будут работать в зависимости от представления угла. Например, \(tg\;\frac{16\pi}3.\)

Если представить этот угол как \(\pi+\frac\pi3+2\pi\times2\), то ему будет соответствовать ФП вида:

\(\;\left(\pi+\alpha+2\pi\times z\right)=tg\;\alpha\)

Откуда получается:

\(tg\;\frac{16\pi}3=tg\;\left(\pi+\frac\pi3+2\pi\times2\right)=tg\;\frac\pi3\)

В таком случае можно указать значение ТФ:

\(tg\;\frac\pi3=\sqrt3\)

Для того, чтобы выразить \(-\frac{2\pi}3+2\pi\times3\) необходимо использовать следующую формулу:

\(tg\;\left(-\alpha+2\pi\times z\right)=-tg\;\alpha\)

Это равенство приводит к результату:

\(tg\;\frac{16\pi}3=tg\;\left(-\frac{2\pi}3+2\pi\times3\right)=-tg\;\left(\frac{2\pi}3\right)=-\left(-\sqrt3\right)=\sqrt3\)

Далее:

\(tg\;\frac{16\pi}3=tg\;\left(\frac{3\pi}2-\frac\pi6+2\pi\times2\right)=сtg\;\left(\frac\pi6\right)=\sqrt3\)

потому что соответствующая ФП имеет вид:

\(tg\;\left(\frac{3\pi}2-\alpha+2\pi\times z\right)\)

Рассмотрим объяснение еще одного примера, где используются ФП.

Задача

Представить \(\sin\;197^\circ\) через синус и косинус острого угла.

Решение

Для того, чтобы применить ФП, нужно заданный угол представить в виде:

\(\pm\alpha+360^\circ\times z,\;90^\circ\pm\alpha+360^\circ\times z,\;180^\circ\pm\alpha+360^\circ\times z\;или\;270^\circ\pm\alpha+360^\circ\times z\)

Важно не забывать, что угол острый. Тогда можно поступить двумя способами, то есть сложением или вычитанием:. \(197^\circ=180^\circ+17^\circ\;\)

\(197^\circ=180^\circ+17^\circ\;\)

или

\(\;197^\circ=270^\circ-73^\circ\)

Получается, что

\(\sin\;197^\circ=\sin\left(180^\circ+17^\circ\right)\;\)

или

\(\;197^\circ=\sin\left(270^\circ-73^\circ\right)\)

Обратимся к описанным выше ФП и получим:

\(\sin\;197^\circ=\sin\left(180^\circ+17^\circ\right)=-\sin\;17^\circ\;и\;\sin\;197^\circ=\sin\left(270^\circ-73^\circ\right)=-\cos\;73^\circ\)

Ответ: \(\sin\;197^\circ=-\sin\;17^\circ\;и\;\sin\;197^\circ=-\cos\;73^\circ.\)

Формулы приведения. Лошадиное правило. Примеры

Стоит ли учить формулы приведения?

Вы в состоянии выучить вот такую таблицу?

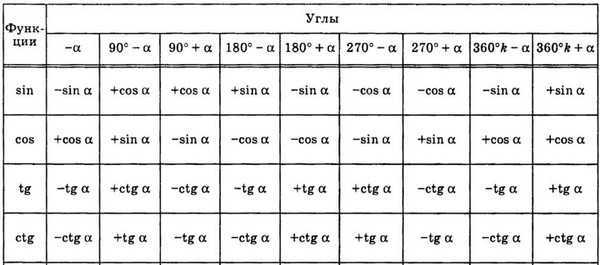
А без приведения сложных аргументов тригонометрических функций к аргументам первой четверти на ЕГЭ по математике никуда.

Но нет необходимости учить эту таблицу!

Нужно просто потратить немного времени и понять алгоритм применения формул приведения.

Не будем терять время! Поехали!

Зачем вообще формулы приведения?

Формулы приведения позволяют упростить вычисления, привести сложные аргументы тригонометрических функций  к аргументам  I четверти.

Вот, например, типичное задание из ЕГЭ по математике:

Вычислите или

Давайте разбираться. А к примерам вернемся чуть позже.

Если хотите докапаться до самой сути, то –> + показать

Можно и пропустить

Преобразование 1.

Упростим .

Считаем  – углом первой четверти! 

Отмечаем углы ,  :

Отмечаем значения и :

Очевидно,  длина «зеленого» катета равна длине «красного» в силу равенства «серых» треугольников:

Но только  – отрицательная величина, а – положительная.

Поэтому 

Преобразование 2.

Упростим .

Вот и :

Вот :

И вот :

Из следующей картинки хорошо видно, что длина отрезка, помеченного синим цветом, равна длине отрезка, помеченного зеленым цветом.

При этом – отрицательная величина, – положительная.

Поэтому 

Преобразование 3.

Упростим .

Вот :

Значение же , как хорошо видно на картинке, то же, что и

Поэтому .

Можно разбирать примеры и дальше для более четкого выявления закономерностей, но давайте уже сформулируем правило, на которое будем опираться при работе с формулами приведения.

Вы всегда сможете проверить «правильность» формулы способом, который мы только что применяли.

Мнемоническое правило для формул приведения 

1. Задаем себе вопрос: «Меняется ли название функции на кофункцию?» (то есть синнус на косинус, косинус на синус, тангенс на котангенс и котангенс на тангенс).

Чтобы ответить на этот вопрос нужно, не смейтесь, – подвигать головой вдоль оси, на которой располагается  ключевая точка. Ключевые точки всегда располагаются здесь (см. рис.):

Например, в формулах – ключевые точки – это .

Так вот если вы мотаете головой вдоль горизонтальной прямой, потому что ключевая точка располагается на ней, то вы, как бы, отвечаете «нет» на вопрос «Меняется ли название функции на кофункцию?»

Если вы киваете головой вдоль вертикальной прямой, потому что ключевая точка располагается на ней, то вы отвечаете «да» на вопрос «Меняется ли название функции на кофункцию?».

2. Ставим справа, на выходе, тот знак, какой несет в себе левая, исходная, часть.

Данное правило еще  называется «лошадиным».

Задача 1.

Вычислить .

Решение:

1.

Ключевая точка располагается на горизонтальной оси:

Название функции меняться не будет.

 2. Исходное значение  – отрицательно, так как располагается в IV четверти:

Итак, 

Ответ: -0,5.

Задача 2.

Вычислить

Решение:

1. 

Ключевая точка располагается на горизонтальной оси:

Название функции меняться не будет.

2. Исходное значение – отрицательно, так как располагается в III четверти:

Итак, 

Ответ: -1.

Задача 3.

Упростить

Решение: 

(название не меняем, знаки и    различаются, как видим из картинки, – ставим справа знак «-»)

 (название меняем, знаки    и , как видно из картинки, одинаковы, – ставим справа знак «+»)

(название меняем, проверять знак нет необходимости, так как все равно у нас функция – в квадрате)

(название не меняем,  знаки    и , как видно из картинки, одинаковы, ставим справа знак  «+»)

(название меняем,  знаки    и , как видно из картинки, одинаковы, ставим справа знак  «+» )

Итак,

Ответ:

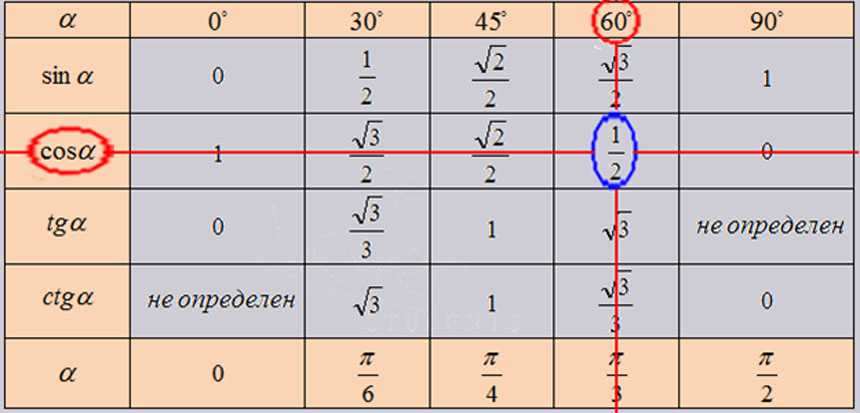
Использование таблицы

В таблице достаточно найти необходимую тригонометрическую функцию и значение угла или радиан, для которых эту функцию нужно вычислить. На пересечении строки с функцией и столбца со значением получим искомое значение тригонометрической функции заданного аргумента.

На рисунке можно увидеть, как найти значение $\cos⁡60°$, которое равно $\frac{1}{2}$.

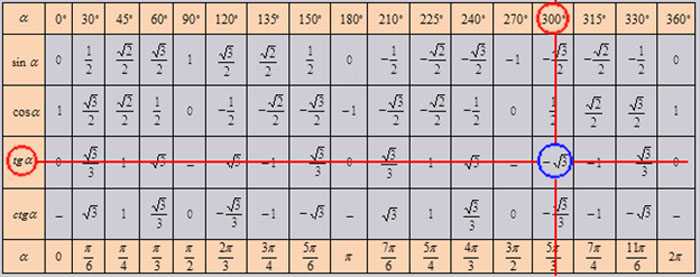
Аналогично используется расширенная тригонометрическая таблица. Преимуществом ее использования является, как уже упоминалось, вычисление тригонометрической функции практически любого угла. Например, легко можно найти значение $\tan 1 380°=\tan (1 380°-360°)=\tan(1 020°-360°)=\tan(660°-360°)=\tan300°$:

Формулы приведения и решение типовых задач. Видеоурок. Алгебра 10 Класс

Тема: Тригонометрические функции

Урок: Формулы приведения и решение типовых задач

Формулы приведения подчиняются двум правилам, которые мы рассмотрели на прошлом уроке. Они позволяют привести значения тригонометрических функций к более удобным углам. Особенно важны углы, кратные

Рассмотрим таблицу значений тригонометрических функций для таких углов. 

α								π
sinα				1							-1
cosα	1							-1							1
tgα		1							1		—
ctgα	—		1					—		1					—

По вертикали отложены функции, по горизонтали – углы, кратные   на отрезке

Держать такую таблицу в голове довольно сложно. Надо иметь способ быстрого получения значений тригонометрических функций для этих углов. Применение формул приведения и есть такой способ. Для этого достаточно запомнить значения тригонометрических функций для углов   

Рассмотрим расположение углов на числовой оси и числовой окружности.

Углы из отрезка  кратные  на координатной оси (рис. 1).

Углы из отрезка  кратные  на единичной окружности (рис. 2).

a) Значения  кратные

b) Значения  кратные

На рисунке показан не только каждый угол, но и значения синуса угла

Стандартные углы

Итак, значения $\sin \alpha $, $\cos \alpha $, $\operatorname{tg}\alpha $ и $\operatorname{ctg}\alpha $ однозначно определяются величиной угла $\alpha $. Нам не важен треугольник — важна только градусная мера угла. Можно один раз посчитать синусы, косинусы и т.д. для нужных углов, а затем просто подставлять их.

Но тут мы сталкиваемся с проблемой, из-за которой многие как раз и не понимают тригонометрию. Проблема состоит из двух пунктов:

1. Для большинства углов $\alpha $ нельзя найти точные значения $\sin \alpha $, $\cos \alpha $, $\operatorname{tg}\alpha $.
2. Верно и обратное: для большинства «красивых» $\sin \alpha $, $\cos \alpha $ и т.д. нельзя подобрать подходящий угол $\alpha $.

Звучит немного непонятно, поэтому разберём каждый пункт на конкретных примерах.

3.1. Три стандартных угла

Существует лишь три острых угла, для которых легко считаются синусы, косинусы и т.д. Это 30°, 45°, 60°. Вот их синусы, косинусы и тангенсы:

\

Чтобы понять, чем эти углы такие особенные, просто посчитаем все эти синусы, косинусы и тангенсы. Начнём с $\alpha =45{}^\circ $. Для этого рассмотрим равнобедренный прямоугольный треугольник. Мы уже встречались с ним:

Поскольку в равнобедренном треугольнике $\angle A=\angle B=45{}^\circ $, получим:

\

Это именно те значения, которые указаны в таблице!

Теперь разберёмся с углами $\alpha =30{}^\circ $ и $\alpha =60{}^\circ $. Здесь рассуждения будут чуть сложнее. Сначала рассмотрим равносторонний треугольник $ABC$ со стороной $AB=2$ (просто так удобнее) и проведём высоту $BH$:

Мы знаем, что высота $BH$ — ещё и медиана, и биссектриса. Поэтому $AH=CH=1$, $\angle ABH=\angle CBH=30{}^\circ $.

Следовательно, треугольник $ABH$ — прямоугольный, да ещё и с острыми углами 30° и 60°. По теореме Пифагора легко найти $BH=\sqrt{3}$. Нанесём все данные на чертёж:

Разберёмся с углом 60°:

\

И с углом 30°:

\

Попробуйте повторить все эти рассуждения самостоятельно. Это очень полезное упражнение!

Возникает вопрос: как быть с другими углами? Например, можно ли найти $\sin {50}^\circ $? Или, быть может, $\cos {10}^\circ $? Спойлер: можно, но это будут очень громоздкие выражения. И у нас пока не хватает технологий, чтобы их найти.

Поэтому идём дальше и посмотрим на ситуацию с другой стороны: как подобрать угол к заданному синусу, косинусу, тангенсу?

3.2. Что с другими углами?

Взгляните ещё раз на «классический» прямоугольный треугольник, с которого мы начинали наши рассуждения:

Катеты 4 и 3, гипотенуза 5 — вполне обычный треугольник. Для него можно посчитать, например, синус острого угла $\alpha $:

\

Итак, мы знаем синус

Внимание, вопрос: каким должен быть угол $\alpha $, чтобы $\sin \alpha =0,6$? Сколько градусов должно быть в угле $\alpha $? Ответ: неизвестно.:). Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $\alpha $, чтобы $\sin \alpha =0,6$

Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует

Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $\alpha $, чтобы $\sin \alpha =0,6$. Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует.

Из всех этих рассуждений сделаем важный вывод. В тригонометрии мы:

• Либо берём угол и считаем для него синусы, косинусы и т.д. Но лишь для трёх острых углов — 30°, 45°, 60° — всё будет считаться быстро и красиво. Такие углы называются табличными.
• Либо берём синус, косинус или тангенс и для него пытаемся подобрать острый угол. Но лишь для табличных значений мы сможем подобрать такие углы. И да: это будут углы 30°, 45°, 60°.

Ещё раз:

И наоборот:

С этой мыслью мы и переходим к следующему пункту — свойства тригонометрических выражений.

Формулы приведения

Два правила формул приведения

1. при 900 и при 2700 (в виде (π/2 ±a) или (3*π/2 ±a)) — функция меняется на кофункцию (sin на cos либо в обратную сторону, tg на ctg либо в обратную).
2. при 1800 и при 3600 (в виде (π ±a) или (2*π ±a)) — функция НЕ изменяется.

2 способа запоминания формул приведения

1. «Правило лошади»:

• Если мы откладываем угол от вертикальной оси, лошадь говорит «да» (киваем головой вдоль оси OY) и приводимая функция меняет свое название: синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс.
• Если мы откладываем угол от горизонтальной оси, лошадь говорит «нет» (киваем головой вдоль оси OХ) и приводимая функция не меняет свое название.
• Знак правой части равенства совпадает со знаком приводимой функции, стоящей в левой части равенства.

2. Использование четности и периодичности.

нечетная функция

• sin (-α) = -sin α
• tg (-α) = -tg α
• сtg (-α) = -сtg α

четная функция

Тригонометрические функции (синус, косинус, тангенс, котангенс) являются периодическими:

• sin α, cos α — периодические функции с наименьшим положительным периодом 2π: sin(α+2kπ) = sin α,cos(α+2kπ) = cos α, k ∈ Z.
• tg α, ctg α — периодические функции с наименьшим положительным периодом π: tg(α+kπ) = tgα, ctg(α+kπ) = ctg α, k ∈ Z.

Формулы приведения в виде списка

sin

• sin(900 — α) = cos α
• sin (900 + α) = cos α
• sin (1800 — α) = sin α
• sin (1800 + α) = -sin α
• sin (2700 — α) = -cos α
• sin (2700 + α) = -cos α
• sin (3600 — α) = -sin α
• sin (3600 + α) = sin α

cos

• cos (900 — α) = sin α
• cos (900 + α) = -sin α
• cos (1800 — α) = -cos α
• cos (1800 + α) = -cos α
• cos (2700 — α) = -sin α
• cos (2700 + α) = sin α
• cos (3600 — α) = cos α
• cos (3600 + α) = cos α

tg

• tg(900 — α) = ctg α
• tg (900 + α) = -ctg α
• tg (1800 — α) = -tg α
• tg (1800 + α) = tg α
• tg (2700 — α) = ctg α
• tg (2700 + α) = -ctg α
• tg (3600 — α) = -tg α
• tg (3600 + α) = tg α

ctg

• ctg (900 — α) = tg α
• ctg (900 + α) = -tg α
• ctg (1800 — α) = -ctg α
• ctg (1800 + α) = ctg α
• ctg (2700 — α) = tg α
• ctg (2700 + α) = -tg α
• ctg (3600 — α) = -ctg α
• ctg (3600 + α) = ctg α

Угол альфа α находится в интервале 0 — 90°.

Справочные таблицы по Тригонометрии

Рис.
1

Определения
тригонометрических функций(рис.
1)

Формулы
выражения тригонометрических функций

Синус
– sin
x
= 
/ r

sin
α

cos
α

tg
α

ctg
α

Косинус
– cos
x
= 
/ r

sin
α

sin
α







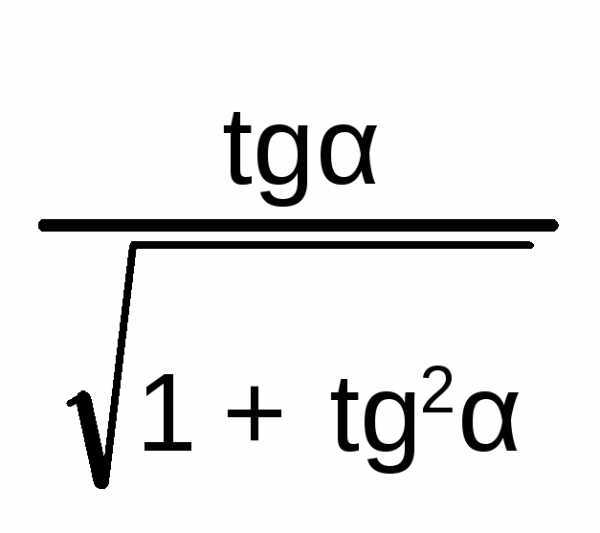
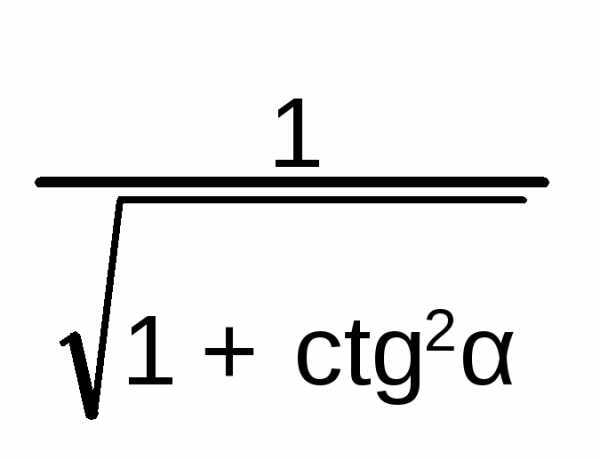
Тангенс
– tg
x
= 
/ 

Котангенс
– ctg
x
= 
/ 

Секанс
– sec
x = r / 

cos
α



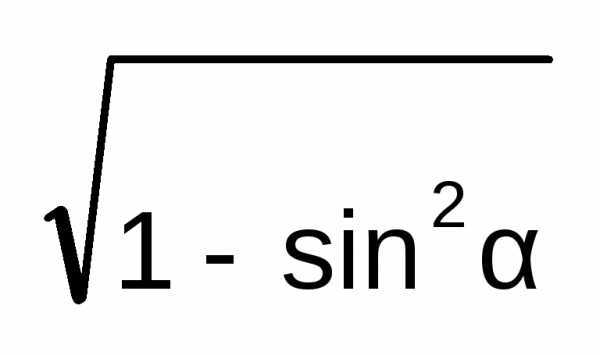
cos
α





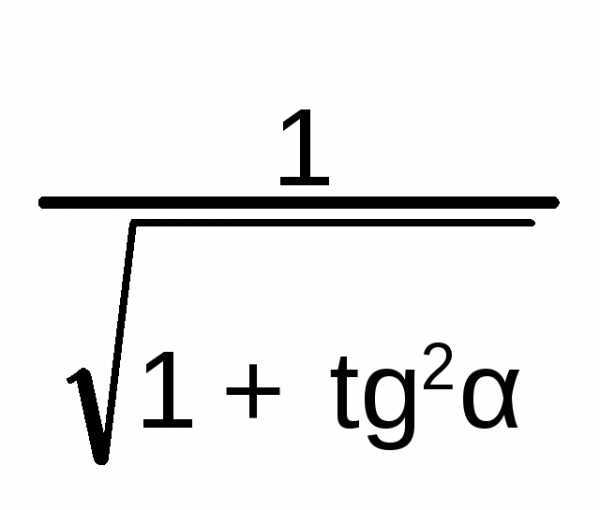
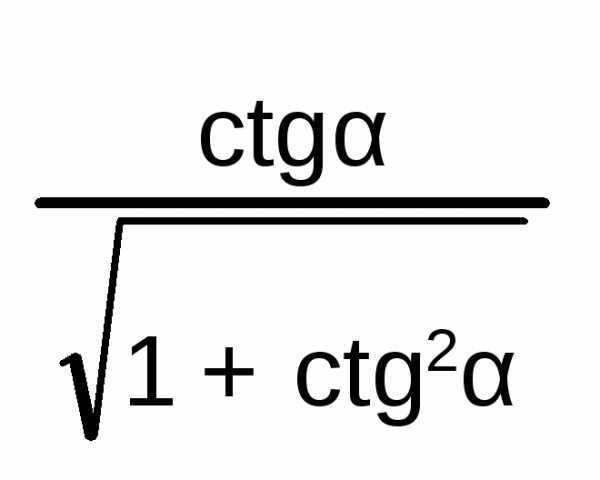
Косеканс
– соsec
x = r / 

cos
x = sin ( /2
– x)

tg
x = ctg ( /2
– x)

sin
x = cos ( /2
– x)

ctg
x = tg ( /2
– x)

tg
α





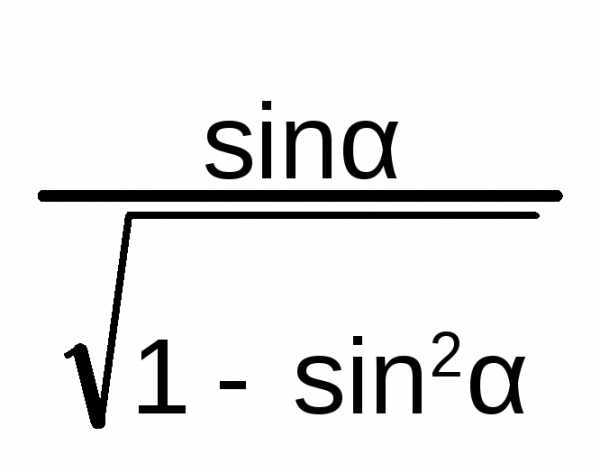
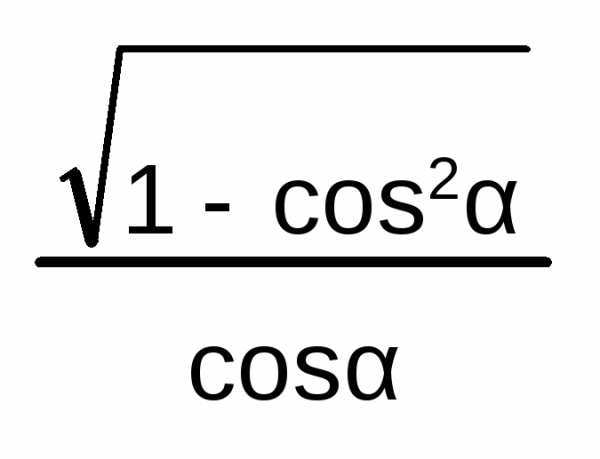
tg
α

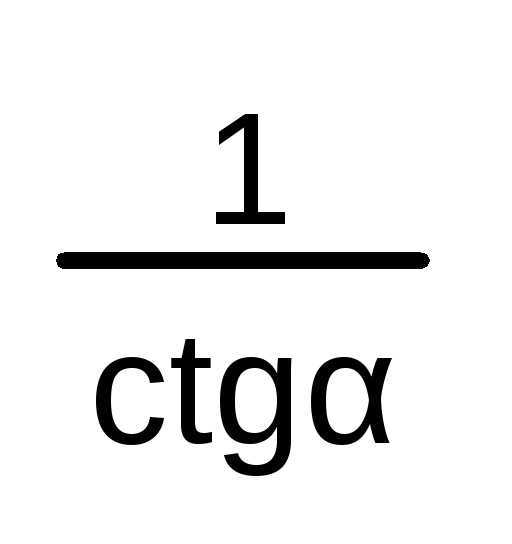
Знаки функций по
четвертям

sin
A
= BC/AB

sin
x

cos
x

tg
x

ctg
x

cos
A
= AC/AB

I

+

+

+

+

ctg
α





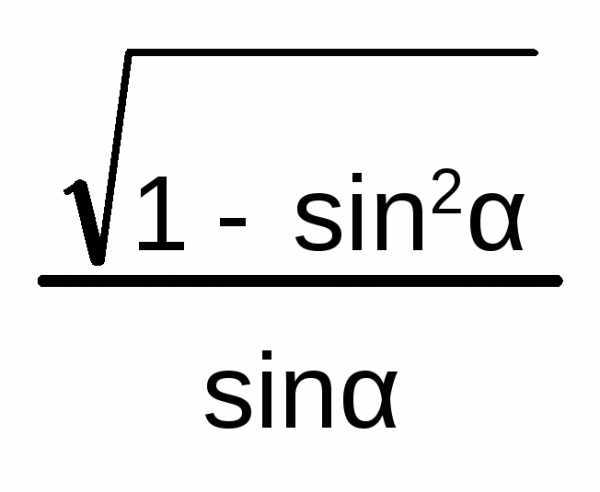
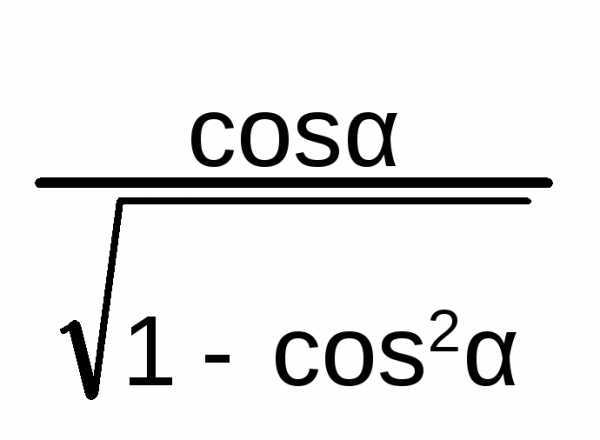
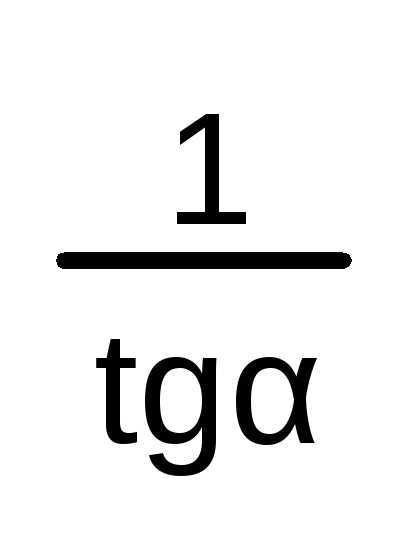
ctg
α

tg
A
= BC/AC

II

+

—

—

—

ctg
A
= AC/BC

III

—

—

+

+

sec
A
= AB/AC

cosec
A
= AB/BC

IV

—

+

—

—

Знак
выбирается в зависимости от четверти
нахождения угла
α

Значение
тригонометрических функций для
некоторых углов

Сумма
и разность аргуметов

Аргумент

sin

cos

tg

ctg

sec

cosec

sin(A+B)
= sinAcosB
+ cosAsinB

sin(A-B)
= sinAcosB
— cosAsinB

0

1

—

1

—

cos(A+B)
= cosAcosB
— sinAsinB

cos(A-B)
= cosAcosB
+ sinAsinB

/6

30

1/2

√3/2

√3/3

√3

2√3/3

2

tg(A+B)
=

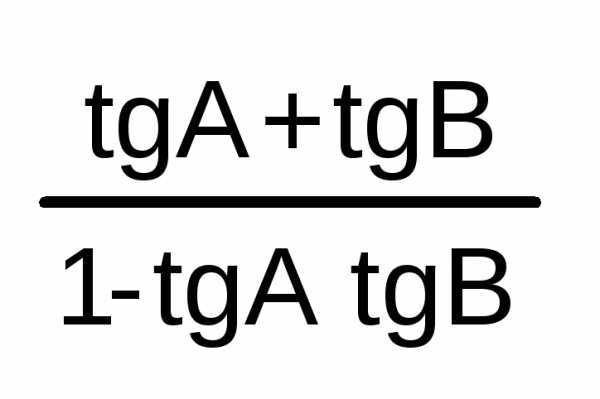
 ≠ π/2
+ nπ;
n 
Z

 ≠ π/2
+ nπ;
n 
Z

 +

≠
π/2
+ nπ;
n 
Z

/4

45

√2/2

√2/2

1

1

√2

√2

/3

60

√3/2

1/2

√3

√3/3

2

2√3/3

tg(A-B)
=

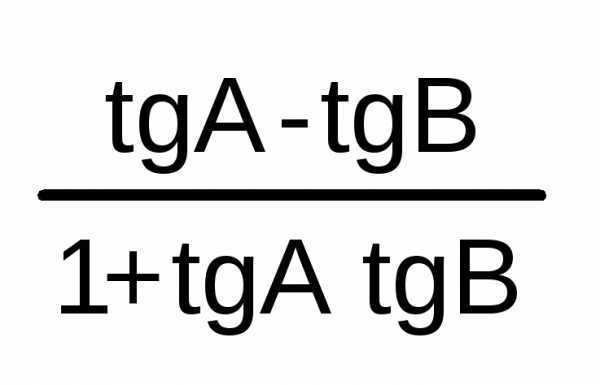
/2

90

1

—

—

1

2/3

120

√3/2

-1/2

-√3

-√3/3

-2

2√3/3

ctg(A+B)
=

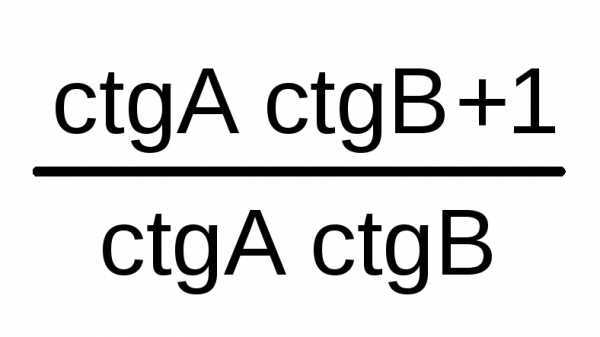
 ≠ nπ;
n 
Z

 ≠ nπ;
n 
Z

 +

≠
nπ;
n 
Z

3/4

135

√2/2

-√2/2

-1

-1

-√2

√2

5/6

150

1/2

-√3/2

-√3/3

-√3

-2√3/3

2

ctg(A-B)
=



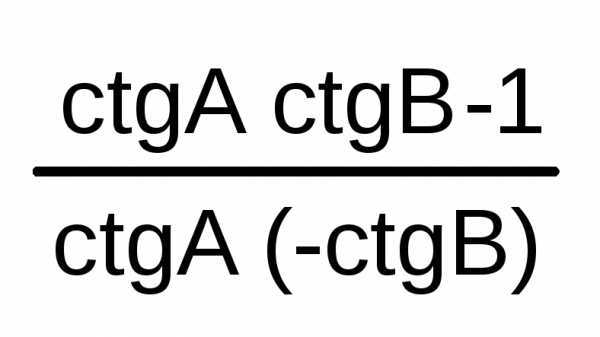
180

-1

—

-1

—

7/6

210

-1/2

-√3/2

√3/3

√3

-2√3/2

-2

Sin(A+B+C)
= sinAcosBcosC + cosAsinBcosC + cosAcosBsinC — sinAsinBsinC

5/4

225

-√2/2

-√2/2

1

1

-√2

-√2

Cos(A+B+C)
= cosAcosBcosC + sinAsinBcosC + sinAcosBsinC — cosAsinBsinC

4/3

240

-√3/2

-1/2

√3

√3/3

-2

-2√3/3

3/2

270

-1

—

—

-1

sin
2A = 2sinAcosA
=

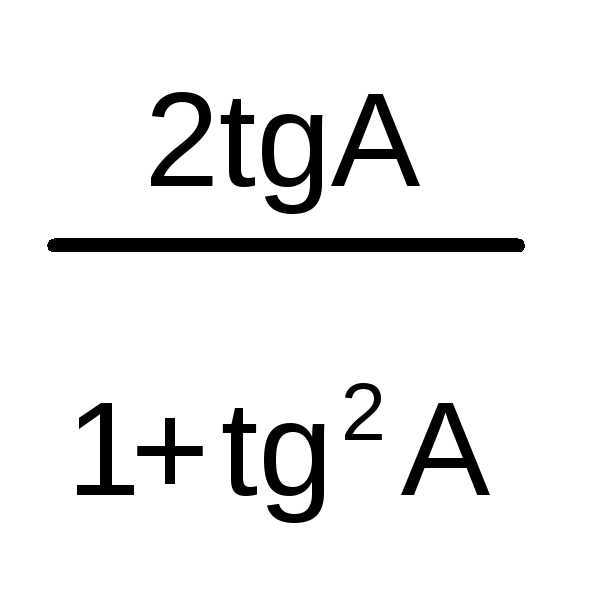
cos
2A = cos2A
– sin2A
=

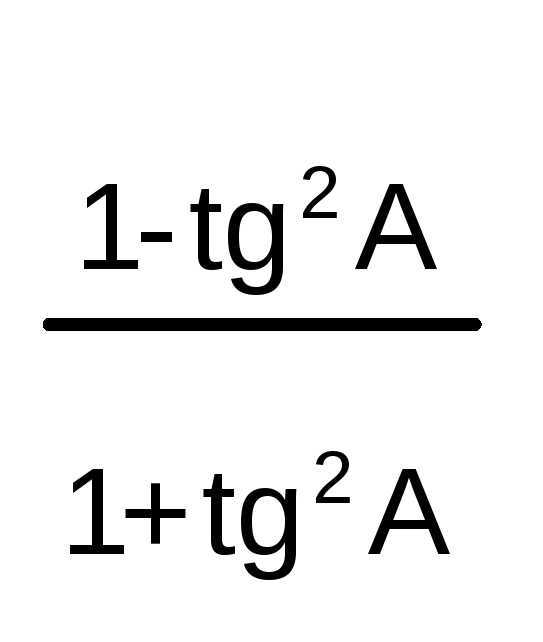
5/3

300

-√3/2

1/2

-√3

-√3/3

2

-2√3/3

7/4

315

-√2/2

√2/2

-1

-1

√2

-√2

11/6

330

-1/2

√3/2

-√3/3

-√3

2√3/3

-2

sin
3A = 3sinA – 4sin3A

cos
3A = 4cos3A
– 3cosA

2

360

1

—

1

—

sin4A
= 8cos3AsinA
— 4cosAsinA

sin4A
= 8cos4A
— 8cos2A
+ 1

Основные
тригонометрические тождества

tg2A
=

=

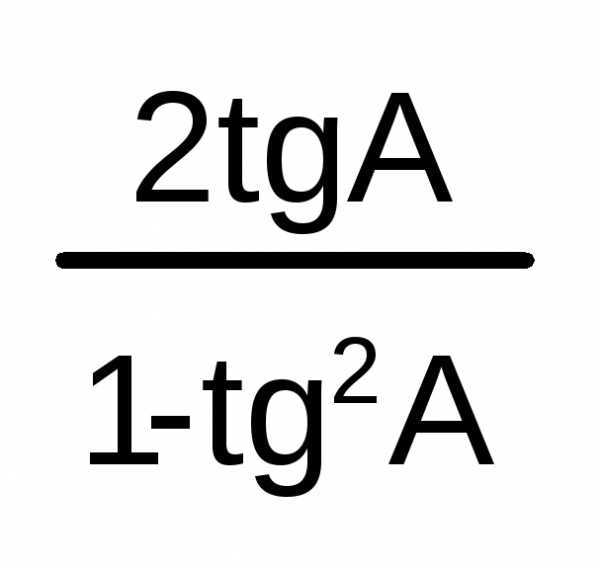
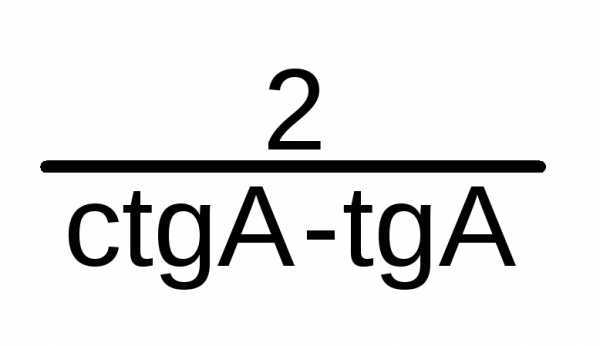
ctg2A
=

=

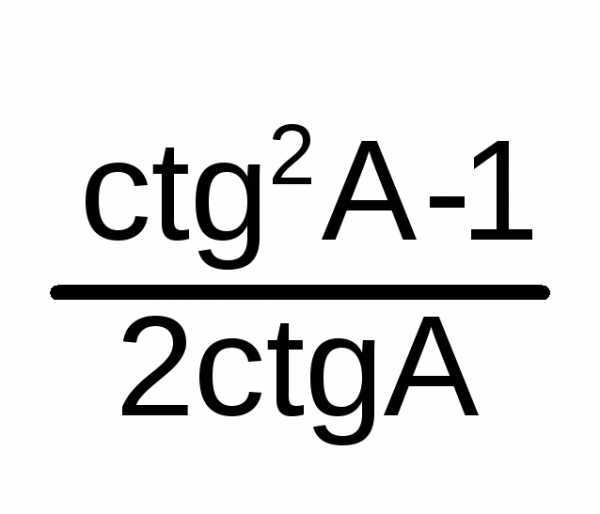
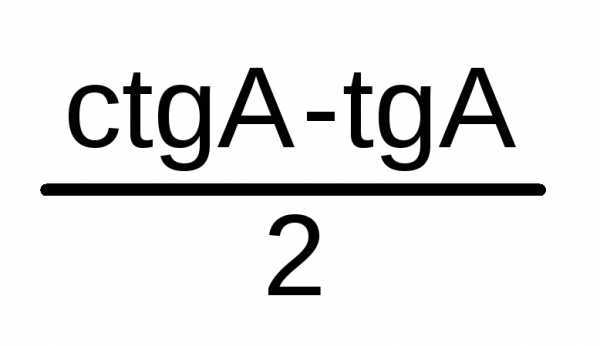
sin2 A + cos2 A = 1

ctg
A = cos A/sinA

tg2 A + 1 = 1/cos2 A

tg
A = sin A/cosA

ctg2 A + 1 = 1/sin2 A

tg
A ctg A = 1

tg3A
=

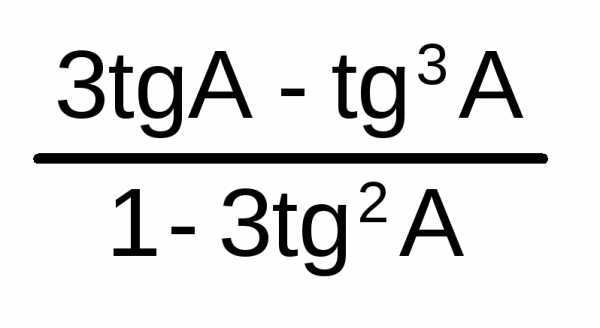
ctg3A
=

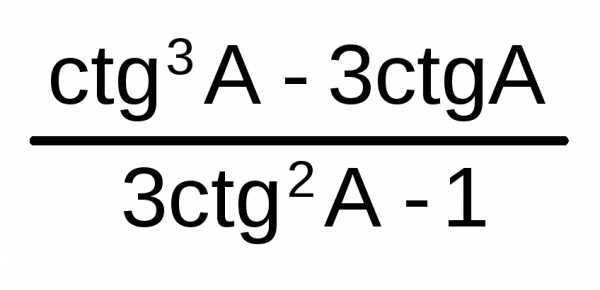
cosec2
A – ctg2 A = 1

sin
A ∙ cosec A = 1

cos
A ∙ sec A = 1

Формулы
приведения

tg4A
=

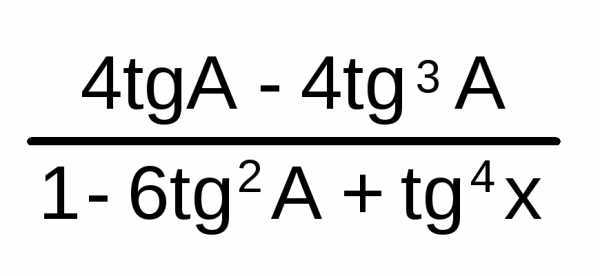
ctg4A
=

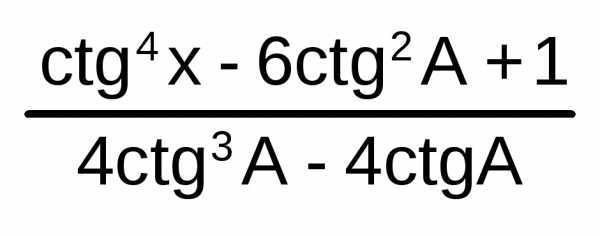
π + α

π — α

2π
+ α

2π
— α

½π + α

½π — α

1,5π
+ α

1,5π
— α

sin

-sinα

sin
α

sin
α

-sin
α

cos
α

cos
α

-cosα

-cosα

Половинные
аргументы

cos

-cosα

-cosα

cos
α

cos
α

-sin
α

sin
α

sin
α

-sin
α

sin
A/2 = 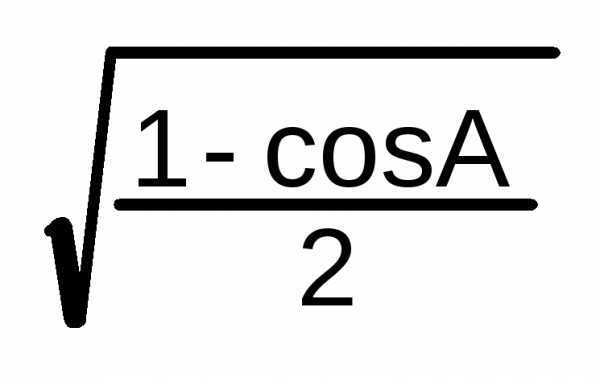

tg
A/2 = 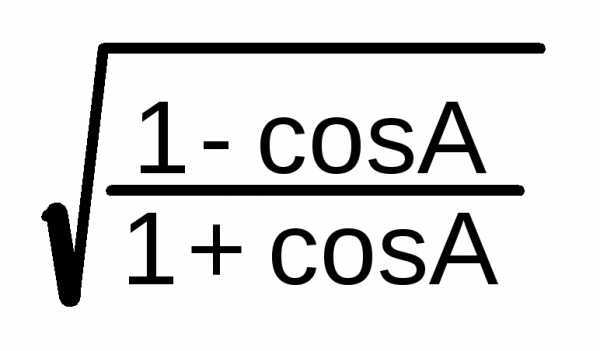

==

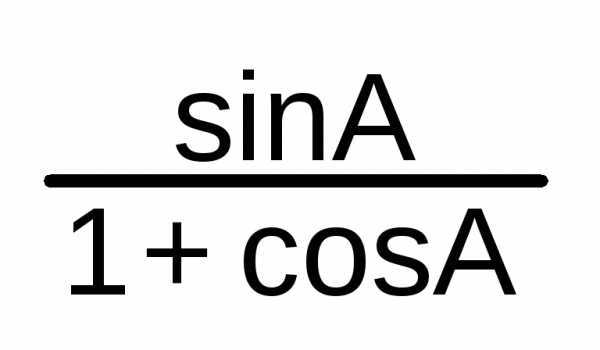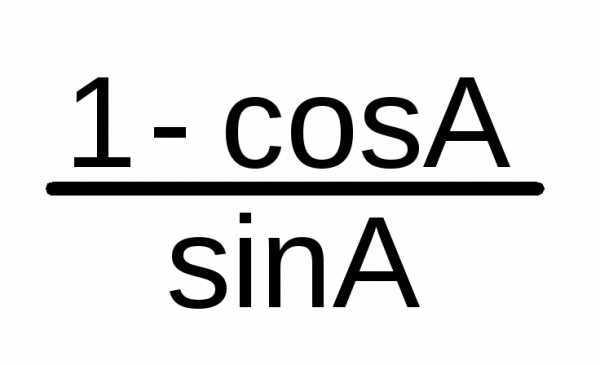
tg

tg
α

-tg
α

tg
α

-tg
α

-ctg
α

ctg
α

-ctg
α

ctg
α

ctg

ctg
α

-ctg
α

ctg
α

-ctg
α

-tg
α

tg
α

-tg
α

tg
α

cos
A/2 = 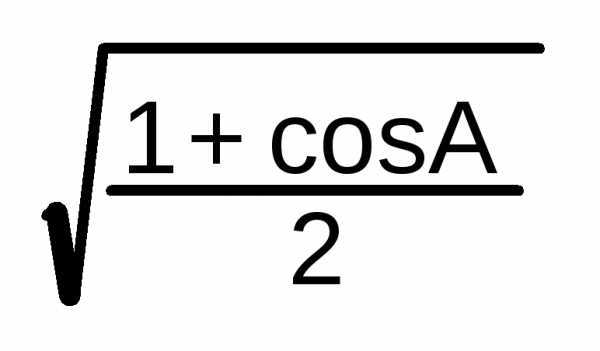

ctg
A/2 = 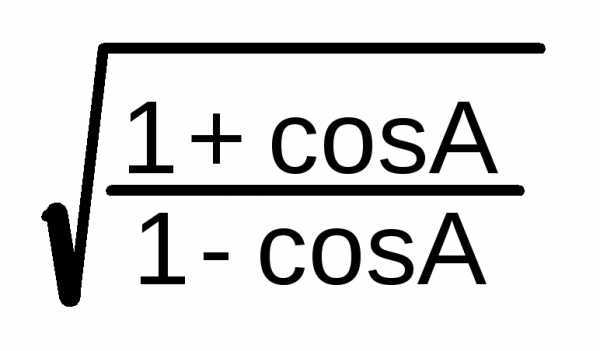

==

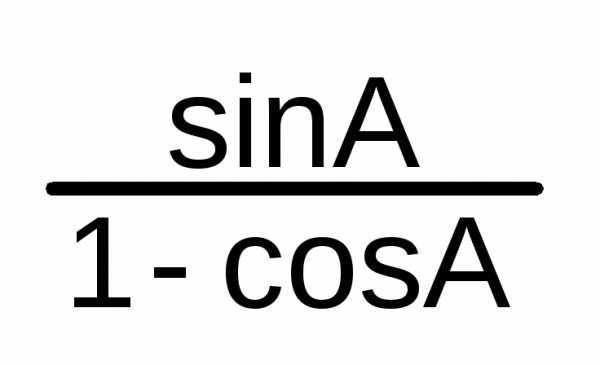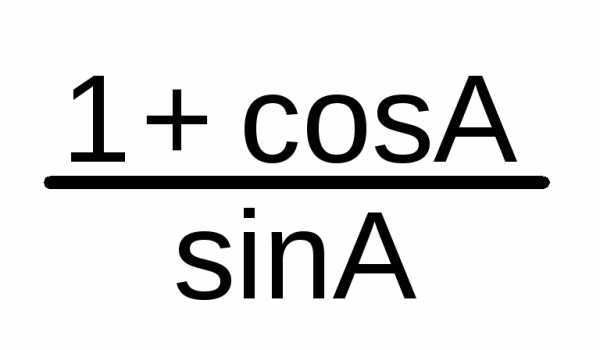
Использование таблиц Брадиса

Используя таблицы Брадиса для синусов, найдем $\sin⁡17°42’$. Для этого в столбце слева таблицы синусов и косинусов находим значение градусов – $17°$, а в верхней строке находим значение минут – $42’$. На их пересечении получаем искомое значение:

$\sin17°42’=0,304$.

Для нахождения значения $\sin17°44’$ нужно воспользоваться поправкой в правой части таблицы. В данном случае к значению $42’$, которое есть в таблице, нужно добавить поправку для $2’$, которая равна $0,0006$. Получим:

$\sin17°44’=0,304+0,0006=0,3046$.

Для нахождения значения $\sin17°47’$ также пользуемся поправкой в правой части таблицы, только в этом случае за основу берем значение $\sin17°48’$ и отнимаем поправку для $1’$:

$\sin17°47’=0,3057-0,0003=0,3054$.

При расчете косинусов выполняем аналогичные действия, но градусы смотрим в правом столбце, а минуты – в нижней колонке таблицы. Например, $\cos20°=0,9397$.

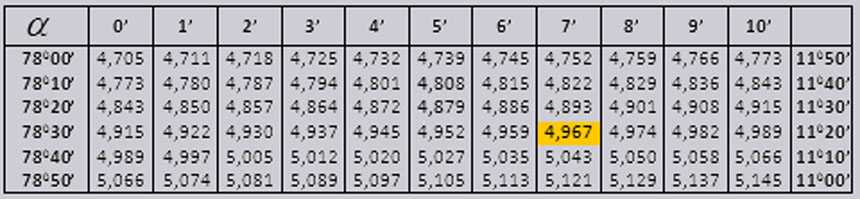
Для значений тангенса до $90°$ и котангенса малого угла поправок нет. Например, найдем $\tan 78°37’$, который по таблице равен $4,967$.

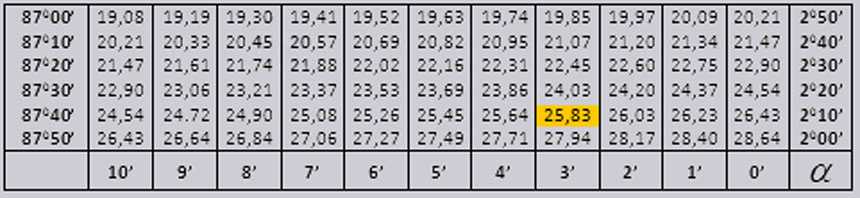
Найдем $\cot 2°13’=25,83$.

Внеклассный урок — Формулы приведения для тригонометрических функций

Формулы приведения – это формулы, позволяющие упростить сложные выражения тригонометрической функции.

Выражения типа π + t,  3π/2 – t,  π/2 + t и т.п. можно упростить настолько, что они будут состоять лишь из одного аргумента t. В предыдущих разделах мы имели дело с несколькими такими упрощениями – например, sin (π + t) = –sin t.

Формул приведения очень много. Запомнить их трудно – но самое главное, в этом нет необходимости. Достаточно запомнить одно-единственное правило – и вы легко сможете самостоятельно выводить формулы и упрощать выражения.

Правило приведения:

Для выраженийπ + t,   π – t,   2π + t,   2π – t	Для выражений π/2 + t,   π/2 – t,   3π/2 + t,  3π/2 – t
1) В приведенном выражении следует сохранить тригонометрическую функцию преобразуемого выражения.2) Перед полученной функцией следует поставить тот знак, который имела бы преобразуемая функция при условии, что 0	1) В приведенном выражении следует изменить тригонометрическую функцию преобразуемого выражения на противоположную.2) Перед полученной функцией следует поставить тот знак, который имела бы преобразуемая функция при условии, что 0

Обратите внимание: в левом и правом столбцах различаются только первые пункты правила. Вторые пункты абсолютно идентичны

• Пример 1: Надо преобразовать выражение cos (π + t).
• Решение.
• Следуем правилу:
• 1) Выражение не имеет дроби – значит, применяем левое правило. То есть функция после приведения остается прежней:
• cos (π + t) = cos t.

2) Осталось определиться со знаком полученной функции.

Если предположить, что аргумент t больше нуля и меньше π/2, то π + t – это аргумент третьей четверти (то есть отмерили полукруг от точки А, а потом еще прошли дугу t длиной меньше π/2 и оказались в третьей четверти). А в третьей четверти косинус имеет знак минус. Значит, после преобразования наша функция обрела следующий тождественный вид:

1. cos (π + t) = –cos t.
2. Пример решен.
3. Пример 2: Надо преобразовать выражение sin (3π/2 – t).
4. Решение.
5. Следуем правилу:
6. 1) Выражение имеет дробь – поэтому применяем правое правило. То есть функция меняется на обратную:
7. sin (3π/2 – t) = cos t

2) Теперь выясним, с каким знаком должно быть наше приведенное выражение. Снова предположим, что 0

• sin (3π/2 – t) = –cos t.
• Пример решен.
• Следуя этому правилу, можно составить другие формулы приведения.
• Формулы приведения.

cos (π + t) = –cos t	sin (π + t) = –sin t	tg (π + t) = tg t	ctg (π + t) = ctg t
cos (π – t) = –cos t	sin (π – t) = sin t	tg (π – t) = –tg t	ctg (π – t) = –ctg t
cos (2π + t) = cos t	sin (2π + t) = sin t	tg (2π + t) = tg t	ctg (2π + t) = ctg t
cos (2π – t) = cos t	sin (2π – t) = –sin t	tg (2π – t) = –tg t	ctg (2π – t) = –ctg t
cos (π/2 + t) = –sin t	sin (π/2 + t) = cos t	tg (π/2 + t) = –ctg t	ctg (π/2 + t) = –tg t
cos (π/2 – t) = sin t	sin (π/2 – t) = cos t	tg (π/2 – t) = ctg t	ctg (π/2 – t) = tg t
cos (3π/2 + t) = sin t	sin (3π/2 + t) = –cos t	tg (3π/2 + t) = –ctg t	ctg (3π/2 + t) = –tg t
cos (3π/2 – t) = –sin t	sin (3π/2 – t) = –cos t	tg (3π/2 – t) = ctg t	ctg (3π/2 – t) = tg t

Примечание:

Часто встречаются более сложные выражения, но они не меняют правила. Например, если cos (2π + t) = cos t, то cos (2π + 3t) = cos 3t.