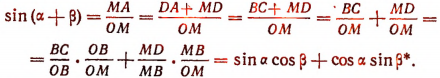Формулы тригонометрии и простейшие уравнения

Тригонометрические функции в прямоугольном треугольнике[]

Чтобы определить тригонометрические функции произвольного угла α,{\displaystyle \alpha ,} возьмём произвольный прямоугольный треугольник, содержащий угол α{\displaystyle \alpha }. Стороны этого треугольника мы будем называть так:

• Гипотенуза — сторона, противолежащая прямому углу, самая длинная сторона в треугольнике. В данном случае, сторона c.{\displaystyle c.}
• Противолежащий катет — катет, лежащий напротив угла. Например, катет a{\displaystyle a} — противолежащий по отношению к углу A.{\displaystyle A.}
• Прилежащий катет — катет, являющийся стороной угла. Например, катет b{\displaystyle b} — прилежащий по отношению к углу A.{\displaystyle A.}

Будем предполагать, что треугольник лежит в евклидовой плоскости, поэтому сумма его углов равна π.{\displaystyle \pi .} Это означает, что углы между катетами и гипотенузой лежат между {\displaystyle 0} и π2.{\displaystyle {\frac {\pi }{2}}.} Используя формулы приведения или определение через единичную окружность, можно расширить область определения тригонометрических функций на множество вещественных чисел.

Си́нус угла — отношение противолежащего катета к гипотенузе: sin⁡α=ac.{\displaystyle \sin \alpha ={\frac {a}{c}}.} Это отношение не зависит от выбора треугольника ABC{\displaystyle {ABC}}, содержащего угол α,{\displaystyle \alpha ,} так как все такие треугольники подобны.

Ко́синус угла — отношение прилежащего катета к гипотенузе: cos⁡α=bc.{\displaystyle \cos \alpha ={\frac {b}{c}}.} Так как sin⁡β=bc,{\displaystyle \sin \beta ={\frac {b}{c}},} синус одного острого угла в треугольнике равна косинусу второго, и наоборот.

Та́нгенс угла — отношение противолежащего катета к прилежащему: tgα=ab.{\displaystyle \operatorname {tg} \,\alpha ={\frac {a}{b}}.}

Кота́нгенс угла — отношение прилежащего катета к противолежащему: ctgα=ba.{\displaystyle \operatorname {ctg} \,\alpha ={\frac {b}{a}}.} Котангенс одного острого угла в прямоугольном треугольнике равен тангенсу второго, и наоборот.

Се́канс угла — отношение гипотенузы к прилежащему катету: sec⁡α=cb.{\displaystyle \sec \alpha ={\frac {c}{b}}.}

Косе́канс угла — отношение гипотенузы к противолежащему катету: cosecα=ca.{\displaystyle \operatorname {cosec} \,\alpha ={\frac {c}{a}}.}

Из определений тригонометрических функций следует:

a=csin⁡α,{\displaystyle a=c\sin \alpha \,,}

b=ccos⁡α,{\displaystyle b=c\cos \alpha \,,}

a=btgα,{\displaystyle a=b\,\operatorname {tg} \,\alpha ,}

b=actgα,{\displaystyle b=a\,\operatorname {ctg} \,\alpha ,}

c=bsec⁡α,{\displaystyle c=b\sec \alpha \,,}

c=acosecα,{\displaystyle c=a\,\operatorname {cosec} \,\alpha ,}

и симметрично:

b=csin⁡β,{\displaystyle b=c\sin \beta \,,}

a=ccos⁡β,{\displaystyle a=c\cos \beta \,,}

b=atgβ,{\displaystyle b=a\,\operatorname {tg} \,\beta ,}

a=bctgβ,{\displaystyle a=b\,\operatorname {ctg} \,\beta ,}

c=asec⁡β,{\displaystyle c=a\sec \beta \,,}

c=bcosecβ.{\displaystyle c=b\,\operatorname {cosec} \,\beta .}

Формулы произведения тригонометрических функций

\sin \alpha \cdot \sin \beta = \dfrac{\cos (\alpha- \beta)-\cos(\alpha + \beta)}{2}\sin \alpha \cdot \cos \beta = \dfrac{\sin (\alpha- \beta)+\sin(\alpha + \beta)}{2}\cos \alpha \cdot \cos \beta = \dfrac{\cos (\alpha- \beta)+\cos(\alpha + \beta)}{2}\tg \alpha \cdot \tg \beta = \dfrac{\cos(\alpha- \beta)- \cos(\alpha+\beta)}{\cos(\alpha- \beta)+ \cos(\alpha+\beta)}=\dfrac{\tg \alpha + \tg \beta}{\ctg \alpha + \ctg \beta}\ctg \alpha \cdot \ctg \beta = \dfrac{\cos(\alpha- \beta)+ \cos(\alpha+\beta)}{\cos(\alpha- \beta)- \cos(\alpha+\beta)}=\dfrac{\ctg \alpha + \ctg \beta}{\tg \alpha + \tg \beta}\tg \alpha \cdot \ctg \beta = \dfrac{\sin(\alpha- \beta)+ \sin(\alpha+\beta)}{\sin(\alpha+ \beta)- \sin(\alpha-\beta)}

Стандартные углы

Итак, значения $\sin \alpha $, $\cos \alpha $, $\operatorname{tg}\alpha $ и $\operatorname{ctg}\alpha $ однозначно определяются величиной угла $\alpha $. Нам не важен треугольник — важна только градусная мера угла. Можно один раз посчитать синусы, косинусы и т.д. для нужных углов, а затем просто подставлять их.

Но тут мы сталкиваемся с проблемой, из-за которой многие как раз и не понимают тригонометрию. Проблема состоит из двух пунктов:

1. Для большинства углов $\alpha $ нельзя найти точные значения $\sin \alpha $, $\cos \alpha $, $\operatorname{tg}\alpha $.
2. Верно и обратное: для большинства «красивых» $\sin \alpha $, $\cos \alpha $ и т.д. нельзя подобрать подходящий угол $\alpha $.

Звучит немного непонятно, поэтому разберём каждый пункт на конкретных примерах.

3.1. Три стандартных угла

Существует лишь три острых угла, для которых легко считаются синусы, косинусы и т.д. Это 30°, 45°, 60°. Вот их синусы, косинусы и тангенсы:

\

Чтобы понять, чем эти углы такие особенные, просто посчитаем все эти синусы, косинусы и тангенсы. Начнём с $\alpha =45{}^\circ $. Для этого рассмотрим равнобедренный прямоугольный треугольник. Мы уже встречались с ним:

Поскольку в равнобедренном треугольнике $\angle A=\angle B=45{}^\circ $, получим:

\

Это именно те значения, которые указаны в таблице!

Теперь разберёмся с углами $\alpha =30{}^\circ $ и $\alpha =60{}^\circ $. Здесь рассуждения будут чуть сложнее. Сначала рассмотрим равносторонний треугольник $ABC$ со стороной $AB=2$ (просто так удобнее) и проведём высоту $BH$:

Мы знаем, что высота $BH$ — ещё и медиана, и биссектриса. Поэтому $AH=CH=1$, $\angle ABH=\angle CBH=30{}^\circ $.

Следовательно, треугольник $ABH$ — прямоугольный, да ещё и с острыми углами 30° и 60°. По теореме Пифагора легко найти $BH=\sqrt{3}$. Нанесём все данные на чертёж:

Разберёмся с углом 60°:

\

И с углом 30°:

\

Попробуйте повторить все эти рассуждения самостоятельно. Это очень полезное упражнение!

Возникает вопрос: как быть с другими углами? Например, можно ли найти $\sin {50}^\circ $? Или, быть может, $\cos {10}^\circ $? Спойлер: можно, но это будут очень громоздкие выражения. И у нас пока не хватает технологий, чтобы их найти.

Поэтому идём дальше и посмотрим на ситуацию с другой стороны: как подобрать угол к заданному синусу, косинусу, тангенсу?

3.2. Что с другими углами?

Взгляните ещё раз на «классический» прямоугольный треугольник, с которого мы начинали наши рассуждения:

Катеты 4 и 3, гипотенуза 5 — вполне обычный треугольник. Для него можно посчитать, например, синус острого угла $\alpha $:

\

Итак, мы знаем синус

Внимание, вопрос: каким должен быть угол $\alpha $, чтобы $\sin \alpha =0,6$? Сколько градусов должно быть в угле $\alpha $? Ответ: неизвестно.:). Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $\alpha $, чтобы $\sin \alpha =0,6$

Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует

Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $\alpha $, чтобы $\sin \alpha =0,6$. Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует.

Из всех этих рассуждений сделаем важный вывод. В тригонометрии мы:

• Либо берём угол и считаем для него синусы, косинусы и т.д. Но лишь для трёх острых углов — 30°, 45°, 60° — всё будет считаться быстро и красиво. Такие углы называются табличными.
• Либо берём синус, косинус или тангенс и для него пытаемся подобрать острый угол. Но лишь для табличных значений мы сможем подобрать такие углы. И да: это будут углы 30°, 45°, 60°.

Ещё раз:

И наоборот:

С этой мыслью мы и переходим к следующему пункту — свойства тригонометрических выражений.

I группа. Основные тождества

sin2α + cos2α = 1;

tgα = ____sinαcosα ;     ctgα = ____cosαsinα ;

tgα·ctgα = 1;

1 + tg2α = _____   1cos2α;     1 + ctg2α = _____   1sin2α .

Эта группа содержит самые простые и самые востребованные формулы. Большинство учащихся их знает. Но если всё-таки есть трудности, то чтобы запомнить первые три формулы, мысленно представьте себе прямоугольный треугольник с гипотенузой равной единице. Тогда его катеты будут равны, соответственно, sinα по определению синуса (отношение противолежащего катета к гипотенузе) и cosα по определению косинуса (отношение прилежащего катета к гипотенузе).

Первая формула представляет собой теорему Пифагора для такого треугольника — сумма квадратов катетов равна квадрату гипотенузы (12 = 1), вторая и третья — это определения тангенса (отношение противолежащего катета к прилежащему) и котангенса (отношение прилежащего катета к противолежащему). Произведение тангенса на котангенс равно 1 потому, что котангенс, записанный в виде дроби (формула третья) есть перевернутый тангенс (формула вторая). Последнее соображение, кстати, позволяет исключить из числа формул, которые необходимо обязательно заучить, все последующие длинные формулы с котангенсом. Если в каком-либо сложном задании Вам встретится ctgα, просто замените его на дробь ___  1tgα и пользуйтесь формулами для тангенса.

Последние две формулы можно не запоминать досимвольно. Они встречаются реже. И если потребуются, то Вы всегда сможете вывести их на черновике заново. Для этого достаточно подставить вместо тангенса или контангенса их определения через дробь (формулы вторая и третья, соответственно) и привести выражение к общему знаменателю

Но важно помнить, что такие формулы, которые связывают квадраты тангенса и косинуса, и квадраты котангенса и синуса существуют. Иначе, Вы можете не догадаться, какие преобразования необходимы для решения той или иной конкретной задачи. Если рекомендации понятны, нажмите кнопку , чтобы убрать «лишние» формулы

Если рекомендации понятны, нажмите кнопку , чтобы убрать «лишние» формулы.

Как вспомнить забытую тригонометрическую формулу? Вывести!

На олимпиаде по математике с большой степенью вероятности, а на внешнем независимом тестировании – уж наверняка встретятся задания по тригонометрии.

Тригонометрию часто не любят за необходимость зубрить огромное количество трудных формул, кишащих синусами, косинусами, тангенсами и котангенсами.

На сайте уже когда-то давались советы, как вспомнить забытую формулу, на примере формул Эйлера и Пиля.

А в этой статье мы постараемся показать, что достаточно твёрдо знать всего пять простейших тригонометрических формул, а об остальных иметь общее представление и выводить их по ходу дела.

Это как с ДНК: в молекуле не хранятся полные чертежи готового живого существа. Там содержатся, скорее, инструкции по его сборке из имеющихся аминокислот.

Так и в тригонометрии, зная некоторые общие принципы, мы получим все необходимые формулы из небольшого набора тех, которые нужно обязательно держать в голове.

Будем опираться на следующие формулы:

1. Основное тригонометрическое тождество: sin2a+cos2a = 1
2. Определение тангенса:
3. Определение котангенса:
4. Формула синуса суммы: sin(a+b) = sinacosb+cosasinb
5. Формула косинуса суммы: cos(a+b) = cosacosb-sinasinb

Из формул синуса и косинуса сумм, зная о чётности функции косинуса и о нечётности функции синуса, подставив -b вместо b, получаем формулы для разностей:

1. Синус разности: sin(a-b) = sinacos(-b)+cosasin(-b) = sinacosb-cosasinb
2. Косинус разности: cos(a-b) = cosacos(-b)-sinasin(-b) = cosacosb+sinasinb

Поставляя в эти же формулы a = b, получаем формулы синуса и косинуса двойных углов:

1. Синус двойного угла: sin2a = sin(a+a) = sinacosa+cosasina = 2sinacosa
2. Косинус двойного угла: cos2a = cos(a+a) = cosacosa-sinasina = cos2a-sin2a

Аналогично получаются и формулы других кратных углов:

1. Синус тройного угла: sin3a = sin(2a+a) = sin2acosa+cos2asina = (2sinacosa)cosa+(cos2a-sin2a)sina = 2sinacos2a+sinacos2a-sin3a = 3sinacos2a-sin3a = 3sina(1-sin2a)-sin3a = 3sina-4sin3a
2. Косинус тройного угла: cos3a = cos(2a+a) = cos2acosa-sin2asina = (cos2a-sin2a)cosa-(2sinacosa)sina = cos3a-sin2acosa-2sin2acosa = cos3a-3sin2acosa = cos3a-3(1-cos2a)cosa = 4cos3a-3cosa

Прежде чем двигаться дальше, рассмотрим одну задачу. Дано: угол — острый. Найти его косинус, если Решение, данное одним учеником:

Т.к. , то sina = 3,а cosa = 4.

(Из математического юмора)

Итак, определение тангенса связывает эту функцию и с синусом, и с косинусом. Но можно получить формулу, дающую связь тангенса только с косинусом. Для её вывода возьмём основное тригонометрическое тождество: sin2a+cos2a = 1 и разделим его на cos2a. Получим:

1. Связь тангенса и косинуса:

1. Аналогично получаем связь котангенса и синуса:

Формула тангенса суммы – ещё одна, тяжело поддающаяся запоминанию. Выведем её так:

1. Формула тангенса суммы: . Разделив числитель и знаменатель на произведение косинусов, получим:

Сразу выводится и

1. Формула тангенса двойного угла:

Из формулы косинуса двойного угла можно получить формулы синуса и косинуса для половинного. Для этого к левой части формулы косинуса двойного угла: cos2a = cos2a-sin2a прибавляем единицу, а к правой – тригонометрическую единицу, т.е. сумму квадратов синуса и косинуса.

cos2a+1 = cos2a-sin2a+cos2a+sin2a

2cos2a = cos2a+1 Выражая cosa через cos2a и выполняя замену переменных, получаем:

1. Косинус половинного угла:

Знак берётся в зависимости от квадранта.

Аналогично, отняв от левой части равенства единицу, а от правой — сумму квадратов синуса и косинуса, получим: cos2a-1 = cos2a-sin2a-cos2a-sin2a 2sin2a = 1-cos2a

1. Cинус половинного угла:

И, наконец, чтобы преобразовать сумму тригонометрических функций в произведение, используем следующий приём. Допустим, нам нужно представить в виде произведения сумму синусов sina+sinb. Введём переменные x и y такие, что a = x+y, b+x-y.

Тогда sina+sinb = sin(x+y)+sin(x-y) = sinxcosy+cosxsiny+sinxcosy-cosxsiny = 2sinxcosy. Выразим теперь x и y через a и b.

Поскольку a = x+y, b = x-y, то . Поэтому

1. Представление суммы синусов в виде произведения:

Сразу же можно вывести

1. Формулу для разбиения произведения синуса и косинуса в сумму: sinacosb = 0.5(sin(a+b)+sin(a-b))

Рекомендуем потренироваться и вывести самостоятельно формулы для преобразования в произведение разности синусов и суммы и разности косинусов, а также для разбиения в сумму произведений синусов и косинусов. Проделав эти упражнения, вы досконально освоите мастерство вывода тригонометрических формул и не потеряетесь даже на самой сложной контрольной, олимпиаде или тестировании.

Уравнения, сводящиеся к виду tgx=a

Ну вот, теперь самое время переходить ко второй порции уравнений, тем более, что я уже и так проболтался в чем состоит решение тригонометрических уравнений нового типа.

Но не лишним будет повторить, что уравнение вида

\( \displaystyle \text{acosx}+\text{bsinx}=0\text{ }\!\!~\!\!\text{ }\left( \text{a},\text{b}\ne 0 \right)\)Решается делением обеих частей на косинус:

\( \displaystyle \text{a}\frac{\text{cosx}}{\text{cosx}}+\text{b}\frac{\text{sinx}}{\text{cosx}}=0\)\( \displaystyle \text{a}+\text{btgx}=0\)\( \displaystyle \text{tgx}=-\frac{\text{a}}{\text{b}}\)Таким образом, решить уравнение вида

\( \displaystyle \text{acosx}+\text{bsinx}=0 \)все равно, что решить

Формулы сложения (четвертая группа)

Основными формулами сложения являются следующие:

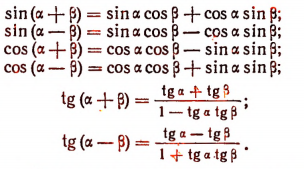
Первая из этих формул читается так: синус, суммы двух чисел равен синусу первого числа, умноженному на косинус второго, плюс косинус первого на синус второго.

Аналогично читаются и остальные формулы.

Теперь перейдем к выводам и доказательствам.

Вывод формул синуса суммы и косинуса суммы (при ограниченных условиях). Пусть (рис. 170). Проведем

Тогда

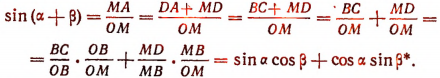
* Углы BMD и ВОС равны между собой как углы с взаимно перпендикулярными сторонами.

Аналогично

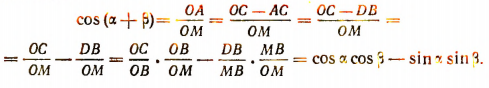
Доказательство общности. Пусть требуется доказать общность каждой из двух выведенных формул:

Это значит требуется доказать, что каждая из них справедлива при любых значениях и , а не только при значениях, удовлетворяющих неравенствам:

Требующееся доказательство мы расчленим на пять последовательных этапов:

1. Пусть

Тогда

Наряду с этим

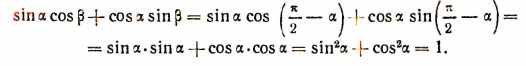
Следовательно, при формула остается в силе, так как ее левая и правая части обращаются в единицу, как это было показано выше.

Подобным же образом можно доказать, что при остается в силе и формула

2. Пусть

Примем

Тогда

Для , как это уже доказано, будет справедливой формула

Заменяя теперь и их выражениями через и , получим:

или

Это свидетельствует о справедливости формулы при

То же самое можно доказать и по отношению к формуле

3. На третьем этапе мы докажем следующее положение. Если формулы

справедливы для каких-нибудь значений и , то они будут справедливы и в том случае, если одно из значений и мы увеличим на .

Рассмотрим выражение в котором

Легко видеть, что

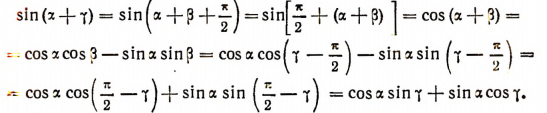
Итак, оказалось, что

т. е. наша формула осталась в силе.

То же самое можно доказать и по отношению к формуле

4. На четвертом этапе докажем, что рассматриваемые нами две формулы справедливы для любых положительных значений и .

Пусть и —любые положительные числа. Тогда найдутся такие целые числа m и n, что где будет

По доказанному ранее наши формулы справедливы для и . По доказанному же в предыдущем этапе они будут оставаться справедливыми, если к прибавим последовательно m раз, а к n раз по . Следовательно, наши формулы останутся в силе и для произвольных положительных чисел и .

5. Наконец, докажем, что наши формулы справедливы и для любых отрицательных чисел

Пусть — любые отрицательные числа. Тогда найдутся такие целые числа m и n, что суммы окажутся числами положительными, которые обозначим соответственно через .

Для положительных чисел по уже доказанному наши формулы

справедливы.

В эти формулы подставим вместо вместо . Тогда получим:

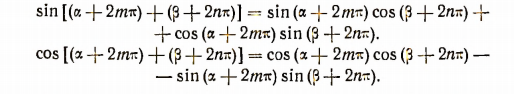
Отсюда вследствие периодичности тригонометрических функцгй получим:

Таким образом, справедливость формул доказана и для отрицательных значений

В тех случаях, когда или равны справедливость наших формул можно доказать непосредственной проверкой.

Итак, доказано, что наши две формулы справедливы при любых значениях Этим и доказана общность каждой из этих формул.

Вывод остальных формул сложения. Опираясь на то, что формулы

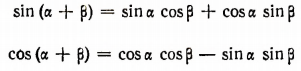
верны при любых значениях , можно все остальные формулы сложения вывести очень кратким путем.

Действительно, рассматривая разность как сумму получим:

Далее,

Наконец,

Аналогично получим, что

Формулы сложения позволяют находить тригонометрическую функцию суммы или разности двух углов через тригонометрические функции самих этих углов. Например,

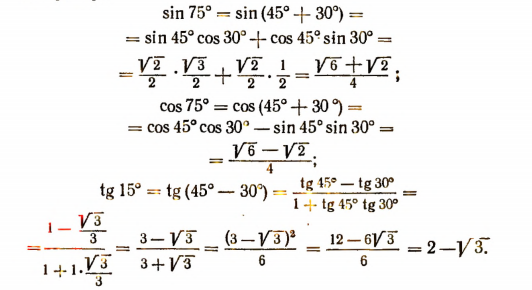
Примеры:

1. Доказать тождество

Доказательство:

2. Доказать тождество

Доказательство:

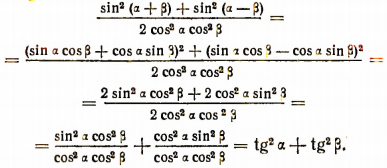
3. Доказать тождество

Доказательство:

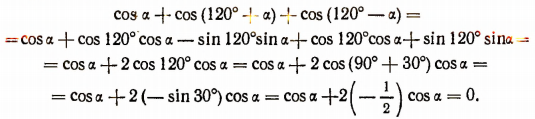
Что такое тригонометрические функции числового аргумента

Равнозначным является и такое объяснение: тригонометрические функции представляют собой выражение того, как связаны хорды и высоты с центральным углом дуги в круге. Рассматриваемые функции активно используют в разных научных областях. Можно наблюдать расширение определения тригонометрических функций по мере того, как развивалась математика. К примеру, в настоящее время роль аргумента могут играть какие-либо вещественные или комплексные числа.

Представим, что имеется некое действительное число, и обозначим его t. Данному числу однозначно соответствует конкретное число sin(t). Правило соответствие достаточно сложное. Поэтому рассмотрим его детально.

Поиск значения sin(t) относительно числа t реализован по следующему алгоритму:

1. Расположение координатной окружности на плоскости таким образом, что центр круга находится в точке начала координат, а у начальной точки А, принадлежащей окружности, следующие координаты (1; 0).
2. Поиск точки на окружности, которая бы соответствовала числу t.
3. Определение ординаты найденной точки.
4. Полученная ордината является искомым значением sin(t).

В действительности здесь говорится о приведении функции s = sin(t) при t в виде какого-либо действительного числа. По предыдущим курсам тригонометрии уже известны определенные свойства рассматриваемой функции, а также некоторые ее значения, к примеру:

Кроме того, с предыдущих уроков уже имеется некоторое представление о таких функциях, как  Перечисленные функции носят название тригонометрических функций числового аргумента t.