Модуль числа, сравнение чисел

Что делать с логарифмами?

Ничего особенного. Как избавляться от логарифмов, подробно описано в теме . Основные правила такие:

\[{\log _a}x \vee b{\rm{ }} \Leftrightarrow {\rm{ }}\left[ {\begin{array}{*{20}{l}}{x \vee {a^b}\;{\rm{при}}\;a > 1}\\{x \wedge {a^b}\;{\rm{при}}\;0 1}\\{x \wedge y\;{\rm{при}}\;0

Также можем добавить правило про логарифмы с разными основаниями и одинаковым аргументом:

Объяснить его можно так: чем больше основание, тем в меньшую степень его придется возвести, чтобы получить один и тот же. Если же основание меньше, то все наоборот, так как соответствующая функция монотонно убывающая.

Пример.

Сравните числа: и.

Решение.

Согласно вышеописанным правилам:

А теперь формула для продвинутых.

Правило сравнения логарифмов можно записать и короче:

Пример.

Что больше: или?

Решение.

Пример.

Сравните, какое из чисел больше: .

Решение.

Интерпретация положительных и отрицательных чисел

Мы уже достаточно долго описываем положительные и отрицательные числа. Однако неплохо было бы знать, какой смысл они несут в себе? Давайте разберемся с этим вопросом.

Положительные числа можно интерпретировать как приход, как прибавку, как увеличение какой-либо величины и тому подобное. Отрицательные числа, в свою очередь, означают строго противоположное – расход, недостаток, долг, уменьшение какой-либо величины и т.п. Разберемся с этим на примерах.

Можно сказать, что мы обладаем 3 предметами. Здесь положительное число 3 указывает количество находящихся у нас предметов. А как можно интерпретировать отрицательное число −3 ? Например, число −3 может означать, что мы должны кому-нибудь отдать 3 предмета, которых у нас даже нет в наличии. Аналогично можно сказать, что в кассе нам выдали 3,45 тысяч рублей. То есть, число 3,45 связано с нашим приходом. В свою очередь отрицательное число −3,45 будет указывать на уменьшение денег в кассе, выдавшей эти деньги нам. То есть, −3,45 – это расход. Еще пример: повышение температуры на 17,3 градуса можно описать положительным числом +17,3 , а понижение температуры на 2,4 можно описать с помощью отрицательного числа, как изменение температуры на −2,4 градуса.

Положительные и отрицательные числа часто используются для описания значений каких-либо величин в различных измерительных приборах. Самым доступным примером является прибор для измерения температур – термометр — со шкалой, на которой записаны и положительные и отрицательные числа. Часто отрицательные числа изображают синим цветом (он символизирует снег, лед, а при температуре ниже нуля градусов Цельсия начинает замерзать вода), а положительные числа записывают красным цветом (цвет огня, солнца, при температуре выше нуля градусов начинает таять лед). Запись положительных и отрицательных чисел красным и синим цветом используют и в других случаях, когда нужно особо выделить знак чисел.

Отрица́тельное число́ — элемент множества отрицательных чисел, которое (вместе с нулём) появилось в математике при расширении множества натуральных чисел. Основной целью расширения было желание сделать вычитание такой же полноценной операцией, как сложение. В рамках натуральных чисел можно вычесть только меньшее число из большего, а переместительный закон не включает вычитание — например, выражение 3 + 4 − 5 <displaystyle 3+4-5> допустимо, а выражение с переставленными операндами 3 − 5 + 4 <displaystyle 3-5+4> недопустимо.

Добавление к натуральным числам отрицательных чисел и нуля делает возможной операцию вычитания для любых пар натуральных чисел. В результате такого расширения получается множество (кольцо) «целых чисел». При дальнейших расширениях множества чисел рациональными или вещественными числами для них тем же путём получаются соответствующие отрицательные значения. Для комплексных чисел упорядоченность не определена, и понятия «отрицательное число» не существует.

Все отрицательные числа, и только они, меньше, чем ноль. На числовой оси отрицательные числа располагаются слева от нуля. Для них, как и для положительных чисел, определено отношение порядка, позволяющее сравнивать одно целое число с другим.

Для каждого натурального числа n существует одно и только одно отрицательное число, обозначаемое -n, которое дополняет n до нуля:

n + ( − n ) = 0. <displaystyle n+left(-n
ight)=0.>

Оба числа называются противоположными друг для друга. Вычитание целого числа a из другого целого числа b равносильно сложению b с противоположным для a:

b − a = b + ( − a ) . <displaystyle b-a=b+left(-a
ight).>

Пример: 25 − 75 = − 50. <displaystyle 25-75=-50.>

Вычитание

Вспомним, что.

Пример.

Что больше: или?

Решение.

Конечно, мы могли бы возвести все в квадрат, перегруппировать, и снова возвести в квадрат. Но можно поступить хитрее:

Видно, что в левой части каждое слагаемое меньше каждого слагаемого, находящегося в правой части.

Соответственно, сумма всех слагаемых, находящихся в левой части, меньше суммы всех слагаемых, находящихся в правой части.

Но будь внимателен! У нас спрашивали что больше…

Правая часть больше.

Пример.

Сравните числа и.

Решение.

Вспоминаем формулы тригонометрии:

Проверим, в каких четвертях на тригонометрической окружности лежат точки и.

Урок 30 Бесплатно Сравнение чисел

В этом уроке мы научимся сравнивать числа как с разными, так и c одинаковыми знаками.

Узнаем, что такое быстрое сравнение с нулем, а также поговорим про то, что касается сравнения чисел и модулей.

Сравнение чисел с одинаковым знаком

Со сравнением двух чисел, оба из которых больше нуля, вы уже знакомы: для этого мы просто смотрим на числа, их разряды и понимаем, какое из них больше. Для нас очевидно еще с начальной школы, что 3 больше, чем 2, 154 больше, чем 145, 1428 больш,е чем 425, и так далее.

Если говорить про отрицательные числа, то для начала приведем аналогию из реальной жизни.

Например, 3-го января температура была равна -10°С , а 4-го января температура была на отметке -7°С , в таком случае мы скажем, что 3-го числа температура была меньше, чем 4-го.

То есть, казалось бы, 10 больше, чем 7, но при этом -10°С меньше, чем -7°С.

Чтобы сравнить два числа, оба из которых отрицательные, надо сравнить их модули, тогда меньше будет то число, у которого модуль больше.

Это же работает и в обратную сторону.

Если два числа отрицательны и модуль первого меньше модуля второго, то первое число больше второго.

Если оба числа отрицательны и их модули равны, то и сами числа равны.

Пример:

Допустим, необходимо сравнить \(\mathbf\) и \(\mathbf\)

Первым делом находим модули:

Это верно и для дробных чисел, смешанных чисел, десятичных дробей и всего, с чем мы уже работали.

Действие первое- находим модули чисел:

Теперь приводим дроби к общему знаменателю:

В таком случае делаем вывод, что \(\mathbf>-\frac>\)

Также сравним \(\mathbf\) и \(\mathbf\)

Мы видим, что модули чисел равны, к тому же, они оба отрицательны, значит эти числа равны.

Пройти тест и получить оценку можно после входа или регистрации

Сравнение чисел с разными знаками

Сейчас мы познакомимся с одним интересным свойством сравнения, которое позволит нам сравнивать числа с разными знаками вообще без каких-либо усилий с нашей стороны.

Задумывались ли вы раньше, почему если мы знаем, что Борис выше Анны, а Сергей выше Бориса, мы сразу сделаем вывод, что Сергей выше и Анны тоже?

Или если мы знаем, что Ваня пришел раньше Пети, а Петя раньше Ильи, то мы делаем вывод, что Ваня пришел раньше Ильи.

Это свойство называется транзитивностью.

Если говорить абстрактно, то это свойство говорит о следующем: если между объектом А и объектом Б есть транзитивное отношение и между объектом Б и объектом В тоже есть это же транзитивное отношение, то это значит, что это отношение есть между А и В.

Звучит может немного непонятно, но на примере со сравнением сейчас все встанет на свои места.

Отношения «быть больше», «быть равным» и «быть меньше» обладают свойством транзитивности.

Поэтому если мы знаем, что 2 меньше, чем 3, а 3 меньше, чем 4, то мы можем утверждать, что 2 меньше, чем 4.

Зафиксируем эти правила коротко и емко.

1. Если а меньше b и b меньше с, то а меньше с

2. Если a больше b и b больше с, то а больше с

3. Если а равно b и b равно с, то а равно с

Более подробно про отношения говорят на курсах высшей математики, дискретной математики или математической логики, но при этом бояться таких абстрактных понятий не стоит.

Теперь мы можем применить это мощное свойство к сравнению чисел с разными знаками.

Пусть а — отрицательное число, b — равно нулю, а с — положительное число.

Мы знаем, что отрицательные числа меньше нуля.

Также мы знаем, что положительные числа больше или, другими словами, нуль меньше положительных чисел.

Тогда, зная транзитивность отношения «меньше», мы можем прийти к выводу, что a меньше с.

Заметьте, что мы нигде ни для а, ни для с не предполагали конкретных значений, а значит, любое отрицательное число меньше любого положительного.

Те же самые рассуждения можно провести в обратную сторону и получить, что любое положительное число больше любого отрицательного.

Итак, посмотрим, как происходит процесс сравнения чисел с разными знаками на практике.

Пример 1

Сравним \(\mathbf\) и \(\mathbf\).

\(\mathbf\)- отрицательное число, \(\mathbf\)— положительное.

Значит, \(\mathbf\), так как любое отрицательное число меньше любого положительного.

Пример 2

Сравним \(\mathbf\) и \(\mathbf\).

\(\mathbf\)- положительное число, \(\mathbf\)- отрицательное.

Значит, \(\mathbf\), так как любое положительное число больше любого отрицательного.

Наибольшее отрицательное и наименьшее положительное целое число

Со сравнением двух целых чисел мы полностью разобрались в предыдущих разделах этой статьи. Сейчас мы еще вкратце остановимся на сравнении трех и большего количества целых чисел, и разберем возникающие при этом ситуации.

Когда сравниваются три и более числа, то сначала проводится сравнение всех возможных пар, составленных из этих чисел. Например, при сравнении четырех целых чисел 7 , 17 , 0 и −2 попарно сравниваются 7 и 17 , 7 и 0 , 7 и −2 , 17 и 0 , 17 и −2 , 0 и −2 , при этом получаются следующие результаты 7 , 7>0 , 7>−2 , 17>0 , 17>−2 и 0>−2 . После этого полученные результаты объединяются в цепочку неравенств (и равенств, когда есть равные числа). Для этого исходные числа записываются в порядке возрастания от самого меньшего до самого большего и между двумя соседними числами ставятся знак −2 .

При сравнении нескольких чисел возникает понятие наибольшего и наименьшего числа.

Число, которое меньше любого другого числа из рассматриваемого множества чисел, называется наименьшим числом в данном множестве.

Число, которое больше любого другого числа в рассматриваемом множестве чисел, называется наибольшим числом в данном множестве.

Проще говоря, наибольшее число – это самое большое число в данном множестве чисел, а наименьшее число – это самое маленькое число.

Приведем пример наибольшего и наименьшего целого числа в множестве, состоящем из шести целых чисел −4 , −81 , −4 , 17 , 0 и 17 . Результат сравнения этих чисел имеет вид −81 . Отсюда хорошо видно, что число −81 является наименьшим целым числом в рассматриваемом множестве, а число 17 – наибольшим целым числом в этом множестве.

Вообще все числа из множества целых чисел можно записать в порядке возрастания (каждое следующее число больше предыдущего), при этом получим последовательность целых чисел вида …, −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, … Эту последовательность целых чисел можно также записать в виде бесконечной цепочки неравенств: …

Отсюда видно, что в множестве целых чисел не существует ни наибольшего целого числа, ни наименьшего целого числа. Действительно, всегда можно указать целое число, которое больше любого наперед заданного сколь угодно большого целого числа (им будет любое следующее число в последовательности целых чисел). Аналогично можно указать целое число, которое меньше любого наперед заданного сколь угодно малого целого числа (это любое число, предшествующее заданному числу в последовательности целых чисел).

Однако во множестве целых положительных чисел ( 1, 2, 3, … ) существует наименьшее целое число – это число 1 . Во множестве целых неотрицательных чисел ( 0, 1, 2, 3, … ) наименьшим числом является число 0 . Целое положительное число в только что указанных множествах мы указать не можем.

Число нуль является наибольшим целым неположительным числом (во множестве целых неположительных чисел …, −3, −2, −1, 0 ). А −1 (минус один) – это наибольшее целое число в множестве целых отрицательных чисел ( …, −3, −2, −1 ). Наименьшего целого числа эти множества не имеют.

Источник

Примеры сравнения отрицательных чисел

Самым простым примером сравнения отрицательных чисел является сравнение целых чисел. С подобной задачи и начнем.

Пример 1

Необходимо сравнить отрицательные числа — 65 и — 23 .

Решение

Согласно правилу, для осуществления действия сравнения отрицательных чисел сначала необходимо определить их модули. | — 65 | = 65 и | — 23 | = 23 . Теперь сравним положительные числа, равные модулям заданных: 65 > 23 . Применим вновь правило, гласящее, что больше то отрицательное число, модуль которого меньше. Таким образом, получим: — 65

Ответ:
— 65

Чуть сложнее сравнивать отрицательные рациональные числа: действие в конечном счете приводит к сравнению обыкновенных или десятичных дробей.

Пример 2

Необходимо определить, какое из заданных чисел больше: — 4 3 14 или — 4 , 7 .

Решение

Определим модули сравниваемых чисел. — 4 3 14 = 4 3 14 и | — 4 , 7 | = 4 , 7 . Теперь сравним полученные модули. Целые части дробей равны, так что приступим к сравнению дробных частей: 3 14 и 0 , 7 . Осуществим перевод десятичной дроби 0 , 7 в обыкновенную: 7 10 , найдем общие знаменатели сравниваемых дробей, получим: 15 70 и 49 70 . Тогда результатом сравнения станет: 15 70 или 3 14
4 3 14
.
fff Применив правило сравнения отрицательных чисел, имеем: — 4 3 14

Также можно было осуществить сравнение путем перевода обыкновенной дроби в десятичную. Разница – лишь в удобстве вычисления.

Ответ:
— 4 3 14

Сравнение отрицательных действительных чисел производится согласно тому же правилу.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

§ 1 Сравнение положительных чисел

В этом уроке мы вспомним, как сравнить положительные числа и рассмотрим сравнение отрицательных чисел.

Начнем с задачи. Днем температура воздуха была +7 градусов, к вечеру понизилась до +2 градусов, ночью стала -2 градуса, а на утро еще понизилась до -7 градусов. Как изменялась температура воздуха?

В задаче речь идет о понижении, т.е. об уменьшении температуры. Значит, в каждом случае конечное значение температуры меньше начального, поэтому 2

Обозначим числа 7, 2, -2, -7 на координатной прямой. Вспомним, что на координатной прямой большее положительное число расположено правее.

Посмотрим на отрицательные числа, число -2 находится правее, чем -7, т.е. для отрицательных чисел на координатной прямой сохраняется тот же порядок: при движении точки вправо ее координата увеличивается, а при движении точки влево ее координата уменьшается.

Можно сделать вывод: Любое положительное число больше нуля и больше любого отрицательного числа. 1 > 0; 12 > -2,5. Любое отрицательное число меньше нуля и меньше любого положительного числа. -59

Сравнивать рациональные числа (т.е. все и целые, и дробные числа) удобно с помощью модуля.

Положительные числа раполагаются на координатной прямой в порядке возрастания от начала координат, значит чем дальше число от начала координат, тем больше длина отрезка от нуля до числа, т.е. его модуль. Следовательно, из двух положительных чисел больше то, модуль которого больше.

§ 2 Сравнение отрицательных чисел

При сравнении двух отрицательных чисел большее будет расположено правее, то есть ближе к началу отсчёта. Значит, его модуль (длина отрезка от нуля до числа) будет меньше. Таким образом, из двух отрицательных чисел больше то, у которого модуль меньше.

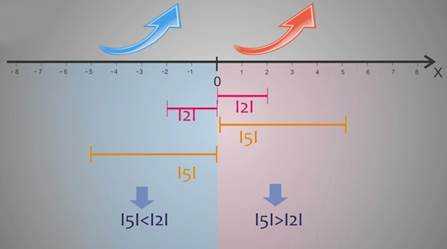
Например. Сравним числа -1 и -5. Точка, соответствующая числу -1расположена ближе к началу отсчёта, чем точка, соответствующая числу -5. А значит длина отрезка от 0 до -1 или модуль числа -1 меньше, чем длина отрезка от 0 до -5 или модуль числа -5 , значит, число -1, больше, чем число -5.

Делаем выводы:

При сравнении рациональных чисел обращаем внимание на:

Знаки: отрицательное число всегда меньше положительного и нуля;

На расположение на координатной прямой: чем правее, тем больше;

На модули: у положительных чисел модуль больше и число больше, у отрицательных чисел модуль больше, а число меньше.

Список использованной литературы:

1. Математика.6 класс: поурочные планы к учебнику И.И. Зубаревой, А.Г. Мордковича //автор-составитель Л.А. Топилина. Мнемозина 2009 г.
2. Математика. 6 класс: учебник для учащихся общеобразовательных учреждений. И.И. Зубарева, А.Г. Мордкович.- М.: Мнемозина, 2013 г.
3. Математика. 6 класс: учебник для учащихся общеобразовательных учреждений. /Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М.: Мнемозина, 2013 г.
4. Справочник по математике — http://lyudmilanik.com.ua
5. Справочник для учащихся в средней школе http://shkolo.ru

Возведение в степень

Пример:

Что больше: \( \displaystyle \sqrt{2}\) или \( \displaystyle 1,4\)?

Решение:

Поскольку обе части неравенства положительны, можем возвести в квадрат, чтобы избавиться от корня:

\( \displaystyle \sqrt{2}\text{ }\vee \text{ }1,4\text{ }\Leftrightarrow \text{ }{{\left( \sqrt{2} \right)}^{2}}\vee {{\left( 1,4 \right)}^{2}}\text{ }\Leftrightarrow \text{ }2\overset{>}{\mathop{\vee }}\,1,96\text{ }\Rightarrow \text{ }\sqrt{2}>1,4\text{ }\).

Пример:

Что больше: \( \displaystyle \sqrt{3}\) или \( \displaystyle \sqrt{5}\)?

Решение:

Здесь тоже можем возвести в квадрат, но это нам поможет избавиться только от квадратного корня. Здесь надо возводить в такую степень, чтобы оба корня исчезли. Значит, показатель этой степени должен делиться и на \( 2\) (степень первого корня), и на \( 3\).

Таким числом является \( 6\), значит, возводим в \( 6\) -ю степень:

Сравнение степеней

Теперь представим, что нам необходимо сравнить не просто числа, а выражения, где существует степень (читай раздел про степени).

Cравни: \( {{2}^{4}}\vee {{2}^{6}}\).

Конечно, ты без труда поставишь знак:

\( {{2}^{4}}<{{2}^{6}}\), ведь если мы заменим степень умножением, мы получим:

\( 2\cdot 2\cdot 2\cdot 2<2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\)Из этого маленького и примитивного примера вытекает правило:

Попробуй теперь сравнить следующее: \( {{5}^{4}}\vee {{6}^{4}}\). Ты так же без труда поставишь знак:

\( {{5}^{4}}<{{6}^{4}}\), потому что, если мы заменим возведение степень на умножение…

В общем, ты все понял, и это совсем несложно.

В этом случае необходимо попробовать привести к общему основанию. Например:

\( {{2}^{2}}\vee {{4}^{3}}\)Разумеется, ты знаешь, что \( 4\) это \( {{2}^{2}}\), соответственно, выражение приобретает вид:

Раскроем скобки и сравним то, что получится:

Сравнение по модулю натурального числа

В теории чисел сравнение [уточнить] по модулю натурального числа  n — задаваемое означенным числом отношение эквивалентности на множестве целых чисел, связанное с делимостью на него. Факторпространство по этому отношению называется «кольцом вычетов». Совокупность соответствующих тождеств и алгоритмов образует модульную [уточнить] (или модулярную) арифметику.

Определения

Два целых числа a и b сравнимы по модулю натурального числа n (или равноостаточны при делении на  n ), если при делении на  n они дают одинаковые остатки.

Эквивалентные формулировки: a и b сравнимы по модулю n , если их разность a — b делится на  n , или если a может быть представлено в виде a = b + kn , где k  — некоторое целое число. Например: 32 и −10 сравнимы по модулю 7, так как

Утверждение « a и b сравнимы по модулю n » записывается в виде:

Свойства равенства по модулю

Отношение сравнения по модулю обладает свойствами

• : для любого целого

a справедливо : если то : если и то

Любые два целых числа a и b сравнимы по модулю 1.

Для того, чтобы числа a и b были сравнимы по модулю n, необходимо и достаточно, чтобы их разность делилась на n.

Если числа и попарно сравнимы по модулю n, то их суммы и , а также произведения и тоже сравнимы по модулю n.

Если числа a и b сравнимы по модулю n, то их степени a k и b k тоже сравнимы по модулю n при любом натуральном k.

Если числа a и b сравнимы по модулю n, и n делится на m, то a и b сравнимы по модулю m.

Для того, чтобы числа a и b были сравнимы по модулю n, представленному в виде его канонического разложения на простые сомножители p_i

>,\quad i = 1, 2, \dots, n.» width=»» height=»» />

Отношение сравнения является отношением эквивалентности и обладает многими свойствами обычных равенств. Например, их можно складывать и перемножать: если

Сравнения, однако, нельзя, вообще говоря, делить друг на друга или на другие числа. Пример: , однако, сократив на 2, мы получаем ошибочное сравнение: . Правила сокращения для сравнений следующие.

• Можно делить обе части сравнения на число, взаимно простое с модулем: если и НОД» width=»» height=»» /> и , где

m = [m₁,m₂] .

Связанные определения

Классы вычетов

Множество всех чисел, сравнимых с a по модулю n называется классом вычетов a по модулю n , и обычно обозначается [a]_n или . Таким образом, сравнение равносильно равенству классов вычетов [a]_n = [b]_n .

Поскольку сравнение по модулю n является отношением эквивалентности на множестве целых чисел _n» width=»» height=»» /> или » width=»» height=»» /> индуцируют соответствующие операции на множестве

[a]_n + [b]_n = [a + b]_n

Относительно этих операций множество 2″ width=»» height=»» />,

в случае нечётного n и чисел

.» width=»» height=»» />

Решение такого сравнения начинается с вычисления НОД(a, m)=d. При этом возможны 2 случая:

• Если b не кратно d , то у сравнения нет решений.
• Если b кратно d , то у сравнения существует единственное решение по модулю m / d , или, что то же самое, d решений по модулю m . В этом случае в результате сокращения исходного сравнения на d получается сравнение:

где a₁ = a / d , b₁ = b / d и m₁ = m / d являются целыми числами, причем a₁ и m₁ взаимно просты. Поэтому число a₁ можно обратить по модулю m₁ , то есть найти такое число c, что \pmod» width=»» height=»» />). Теперь решение находится умножением полученного сравнения на c:

\equiv a_1^\pmod .» width=»» height=»» />

Пример

Для сравнения » width=»» height=»» />

Поскольку 2 взаимно просто с модулем 11, можно сократить левую и правую части на 2. В итоге получаем одно решение по модулю 11: ;\ x\equiv 12\pmod » width=»» height=»» />.

Сравнения второй степени

Решение сравнений второй степени сводится к выяснению, является ли данное число квадратичным вычетом (с помощью квадратичного закона взаимности) и последующему вычислению квадратного корня по данному модулю.

История

Китайская теорема об остатках, известная уже много столетий, утверждает (на современном математическом языке), что кольцо вычетов по модулю произведения нескольких взаимно простых чисел является прямым произведением соответственных множителям колец вычетов.

В значительной степени теория делимости и вычетов была создана Эйлером. Сравнения по модулю впервые использовались Гауссом в его книге «Арифметические исследования», 1801 год. Он же предложил утвердившуюся в математике символику для сравнений.

Топ вопросов за вчера в категории Математика

Математика 21.06.2023 06:59 942 Тупиков Сергей.

Запишите в десятичной записи число: а) 74; б) 350; в)636300; г)2800005.

Ответов: 1

Математика 15.06.2023 02:27 528 Журавель Настя.

Велосипед ехал 2,6 ч со скоростью 6,6 м/с,а затем 1,4 ч со скоростью 5,2 м/с.чему равна средняя скор

Ответов: 2

Математика 04.06.2023 14:00 561 Матвеева Лиля.

Запишите в десятичной записи число: а) 74, б) 350, в) 636 300 г) два миллиона восемьсот тысяч 5 д) 2

Ответов: 1

Математика 18.05.2023 04:51 875 Максимова Катя.

Найдите отношение длины диагонали листа формата а7 к его меньшей стороне ответ округлите до десятых

Ответов: 2

Математика 20.06.2023 17:50 190 Аветисян Карен.

Равны ли множества А и В А={1}, В=`1`

Ответов: 1

Математика 14.06.2023 02:36 237 Чиняев Глеб.

На одну порцию десерта из клубники берут 120г ягод и 25г сливок.Сколько сливок потребуется для приго

Ответов: 1

Математика 14.06.2023 11:22 399 Анфалова Татьяна.

Экскурсионный теплоход двигался 4,3 ч по озеру со скоростью 20км/ч, затем 2,5 ч по реке со скоростью

Ответов: 1

Математика 15.06.2023 03:21 285 Кулакова Лиза.

Найдите среднюю длину своего шага,измерив длину пяти своих шагов​

Ответов: 1

Математика 21.06.2023 08:32 177 Верхозин Александр.

2. Сколько лошадей в двух табунах, если в одном табуне 836 лошадей, а в другом на 308 больше? 3.Вычи

Ответов: 2

Математика 18.07.2023 20:29 90 Филимонов Захар.

10A ДОМАШНЕЕ ЗАДАНИЕ Узнай из диаграммы количество мест в построенных школах по годам. Запиши эти

Ответов: 1