Арктангенс
Рассмотрим на множестве $X=\left(-\frac{\pi }{2},\frac{\pi }{2}\right)$ функцию $y=tgx$. Она непрерывна и возрастает на множестве $X$ и отображает множество $X=\left(-\frac{\pi }{2},\frac{\pi }{2}\right)$ на множество $Y=R$, поэтому по теореме о существовании обратной непрерывной монотонной функции у функции $y=tgx$ в множестве $Y$ существует обратная функция, которая также непрерывна и возрастает в множестве $Y=R$ и отображает множество $R$ на множество $\left(-\frac{\eth }{2},\frac{\pi }{2}\right)$. Эта обратная функция называется арктангенсом и обозначается $x=arctgy$.
В более привычной для нас записи имеем $y=arctgx$. График функции арктангенса изображен на рисунке 3.
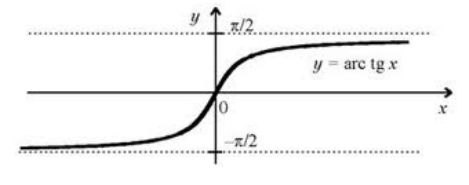Рисунок 3. График функции арктангенса.
Арккосинус
Arccos числа а — это значение угла α, косинус которого равен а.
Кривая y = arcos x
зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.
Рассмотрим функцию арккосинуса более подробно:
- Функция определена на отрезке .
- ОДЗ для arccos — .
- График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
- Y = 0 при x = 1.
- Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.
Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.
Задание 1.
Укажите функции изображенные на рисунке.
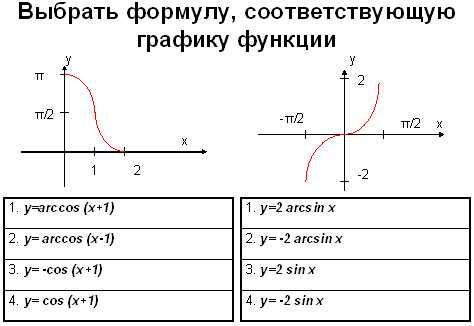
Ответ:
рис. 1 – 4, рис.2 — 1.
В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.
Углы на тригонометрическом круге
Для того, чтобы освоить теорию тригонометрической окружности, нужно понять, как считаются ∠ на ней, и в чем они измеряются. Считаются они очень просто.
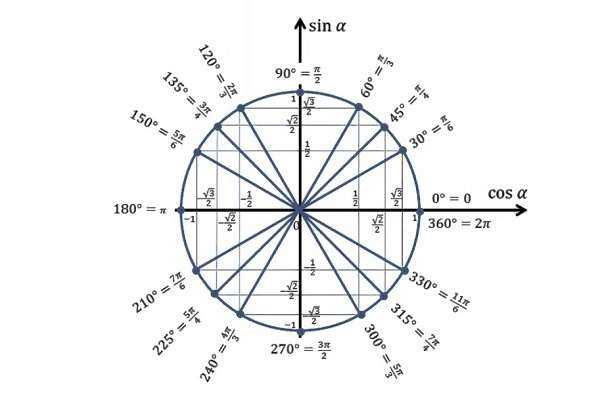
Окружность делится системой координат на четыре части. Каждая часть образует ∠ 90°. Половина от этих углов равняется 45 градусам. Соответственно две доли окружности равняются 180°, а три 360°. Как пользоваться этой информацией?
Если требуется решить задачу по нахождению ∠, прибегают к теоремам о треугольниках и основным Пифагоровым законам, связанных с ними.
Измеряются углы в радианах:
- от 0 до 90° значения углов от 0 до ∏/2,
- от 90 до 180° значения углов от ∏/2 до ∏,
- от 180 до 270° от ∏ до 3*∏/2,
- последняя четверть от 2700 до 3600 — значения от 3*∏/2 до 2*∏.
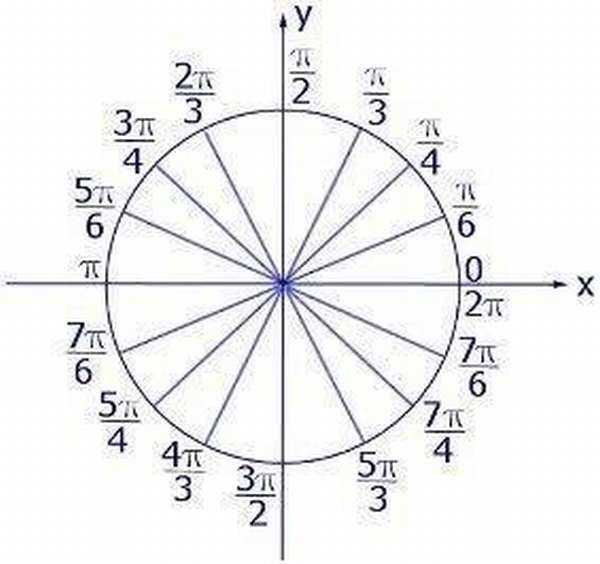
Чтобы узнать конкретное измерение, перевести радианы в градусы или наоборот, следует прибегнуть к таблице-шпаргалке.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла ( sin α ) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла ( cos α ) — отношение прилежащего катета к гипотенузе.
Тангенс угла ( t g α ) — отношение противолежащего катета к прилежащему.
Котангенс угла ( c t g α ) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Орфография
Математические формулы используются для арктангенса как символы , , , или .
Для арккотангенса в последнее время также используются обозначения и .
арктан{\ displaystyle \ arctan} загар{\ displaystyle \ operatorname {atan}} загар(-1){\ Displaystyle \ tan ^ {(- 1)}} загар⟨-1⟩{\ displaystyle \ tan ^ {\ langle -1 \ rangle}}загар-1{\ displaystyle \ tan ^ {- 1}}арккот,{\ displaystyle \ operatorname {arccot},} arcctg,{\ displaystyle \ operatorname {arcctg},} кроватка{\ displaystyle \ operatorname {acot}}детская кроватка-1{\ displaystyle \ cot ^ {- 1}}
Однако из-за общих обозначений, используемых сегодня для обратных функций , обозначения, которые широко распространены в карманных калькуляторах, начинают вытеснять классические обозначения , что может легко привести к путанице с обратным значением тангенса, котангенса (см. Также для итерация).
ж-1{\ displaystyle f ^ {- 1}}загар-1{\ displaystyle \ tan ^ {- 1}}арктан{\ displaystyle \ arctan}
Формулы связи между прямыми и обратными тригонометрическими функциями
Знать связи между прямыми функциями и их аркфункциями очень важно для решения многих практических задач. Как же быть, если у нас есть необходимость вычислить, к примеру, тангенс арксинуса? Ниже приведен список основных формул для этого, которые полезно выписать себе
| — 1 ≤ α ≤ 1 , sin ( a r c sin α ) = α | — 1 ≤ α ≤ 1 , sin ( a r c cos α ) = 1 — α 2 | — ∞ ≤ α ≤ + ∞ , sin ( a r c t g α ) = α 1 + α 2 | — ∞ ≤ α ≤ + ∞ , sin ( a r c c t g α ) = 1 1 + α 2 |
| — 1 ≤ α ≤ 1 , cos ( a r c sin α ) = 1 — α 2 | — 1 ≤ α ≤ 1 , cos ( a r c cos α ) = α | — ∞ ≤ α ≤ + ∞ , cos ( a r c t g α ) = 1 1 + α 2 | — ∞ ≤ α ≤ + ∞ , cos ( a r c c t g α ) = 1 1 + α 2 |
| — 1 α 1 , t g ( a r c sin α ) = α 1 — α 2 | α ∈ ( — 1 , 0 ) ∪ ( 0 , 1 ) , t g ( a r c cos α ) = 1 — α 2 α | — ∞ ≤ α ≤ + ∞ , t g ( a r c t g α ) = α | α ≠ 0 , t g ( a r c c t g α ) = 1 α |
| α ∈ ( — 1 , 0 ) ∪ ( 0 , 1 ) , c t g ( a r c sin α ) = 1 — α 2 α | — 1 α 1 , c t g ( a r c cos α ) = α 1 — α 2 | α ≠ 0 , c t g ( a r c t g α ) = 1 α | — ∞ ≤ α ≤ + ∞ , c t g ( a r c c t g α ) = α |
Теперь разберем примеры, как они применяются в задачах.
Вычислите косинус арктангенса из 5 .
Решение
У нас для этого есть подходящая формула следующего вида: cos ( a r c t g α ) = 1 1 + α 2
Подставляем нужное значение: cos ( a r c t g 5 ) = 1 1 + ( 5 ) 2 = 2 6
Вычислить синус арккосинуса 1 2 .
Решение
Для этого нам понадобится формула: sin ( a r c cos α ) = 1 — a 2
Подставляем в нее значения и получаем: sin ( a r c cos 1 2 ) = 1 — ( 1 2 ) 2 = 3 2
Обратите внимание, что непосредственные вычисления приводят к аналогичному ответу: sin ( a r c cos 1 2 ) = sin π 3 = 3 2
Если вы забыли, как правильно вычислять значения прямых и обратных функций, вы всегда можете вернуться к нашим предыдущим материалам, где мы разбирали это.
Арккосинус
Рассмотрим на множестве $X=\left$ функцию $y=cosx$. Она непрерывна и убывает на множестве $X$ и отображает множество $X=\left$ на множество $Y=$, поэтому по теореме о существовании обратной непрерывной монотонной функции у функции $y=cosx$ в множестве $Y$ существует обратная функция, которая также непрерывна и возрастает в множестве $Y=$ и отображает множество $$ на множество $\left$. Эта обратная функция называется арккосинусом и обозначается $x=arccosy$.
В более привычной для нас записи имеем $y=arccosx$. График функции арккосинуса изображен на рисунке 2.
Рисунок 2. График функции арккосинуса.
Как определяется арктангенс?
Арктангенс в алгебре – это обратная тригонометрическая функция к tg (тангенсу), его еще называют аркфункцией. Область ее определения от — ∞ +∞. Обозначается он в математике как arctg x. Во многих учебниках и методической литературе зарубежных стран можно встретить другое обозначение: arctang x.
Из особенностей этой обратной функции выделяют то, что она является возрастающей. Функция y=arctg x ограничена и непрерывна на всей протяженности своей числовой прямой.
История происхождения названия обратных функций тоже имеет свою историю. Оно образовано при помощи приставки «арк», которая происходит от латинского слова arcus и переводится как дуга. Это объясняется тем, что значение обратной функции неразрывно связано с длиной дуги единичной окружности.
Обозначение обратных функций в тригонометрии при помощи приставки «arc» в математику привнес австрийский ученый Крал Шерфер, который жил в XVIII веке. Распространению этой приставки «arc» к обратным функциям мир математики обязан Лагранжу (он жил во Франции в это же время, Жозеф Луи Лагранж также известен известен, как и крупнейший математик XVIII Эйлер).
Позднее в XIX веке немецкие и английские математические школы использовали другие обозначения обратных функций: tg-1, 1/tg. Такие же обозначения как tg-1 встречаются в разных научных изданиях. С одной стороны это имеет место быть, а с другой – некорректно, возникает путаница с возведением функции в минусовую степень.
Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
a r c sin , a r c cos , a r c t g и a r c c t g
Для точного значения a r c sin , a r c cos , a r c t g и a r c c t g числа а необходимо знать величину угла. Об этом сказано в предыдущем пункте. Однако, точное значении функции нам неизвестно. Если необходимо найти числовое приближенное значение аркфункций, применяют таблицу синусов, косинусов, тангенсов и котангенсов Брадиса.
Такая таблица позволяет выполнять довольно точные вычисления, так как значения даются с четырьмя знаками после запятой. Благодаря этому числа выходят точными до минуты. Значения a r c sin , a r c cos , a r c t g и a r c c t g отрицательных и положительных чисел сводится к нахождению формул a r c sin , a r c cos , a r c t g и a r c c t g противоположных чисел вида a r c sin ( — α ) = — a r c sin α , a r c cos ( — α ) = π — a r c cos α , a r c t g ( — α ) = — a r c t g α , a r c c t g ( — α ) = π — a r c c t g α .
Рассмотрим решение нахождения значений a r c sin , a r c cos , a r c t g и a r c c t g с помощью таблицы Брадиса.
Если нам необходимо найти значение арксинуса 0 , 2857 , ищем значение, найдя таблицу синусов. Видим, что данному числу соответствует значение угла sin 16 градусов и 36 минут. Значит, арксинус числа 0 , 2857 – это искомый угол в 16 градусов и 36 минут. Рассмотрим на рисунке ниже.
Правее градусов имеются столбцы называемые поправки. При искомом арксинусе 0 , 2863 используется та самая поправка в 0 , 0006 , так как ближайшим числом будет 0 , 2857 . Значит, получим синус 16 градусов 38 минут и 2 минуты, благодаря поправке. Рассмотрим рисунок с изображением таблицы Брадиса.
Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.
Таким образом находятся значения a r c sin , a r c cos , a r c t g и a r c c t g .
Тангенс — это отношение.
Итак, есть два определения:
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.
Тангенс – это отношение синуса к косинусу.
Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.
» alt=»»>
Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).
Остались вопросы?
Получить подробные ответы на свои вопросы в области обратных тригонометрических функций, узнать их особенности и свойства, изучить график арктангенса и грамотно подготовиться к ЕГЭ вы можете в режиме онлайн вы можете на сайте http://interneturok.ru/На этом портале найдете уроки как по алгебре, так и по другим предметам школьной программы.
Почему многие выбирают онлайн игры
13.10.2021 17:26
Какие возможности дают онлайн игры
30.07.2021 11:34
Взгляд эксперта на бейсбол
29.06.2021 14:03
Системы сбора данных клиентов
01.06.2021 13:35
В чем преимущества старого аккаунта в Фейсбуке
28.03.2021 20:26
5 полезных правил для организации сбора средств на благотворительные цели
26.03.2021 17:13
Приятное времяпровождение в онлайн играх
30.01.2021 18:01
Где делают ставки на игры
22.01.2021 16:37
Пять советов по выбору букмекерской конторы
18.01.2021 12:43
Чем привлекает букмекерская контора Фортуна лайв
12.01.2021 07:14
Тангенс угла
Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.
В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.
Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса (это что?), тангенса, котангенса.
Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения. Введя функции угла, определяют их свойства
Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты
Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.
Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.
Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).
Решение уравнений, содержащих аркфункции
Подобные документы
Анализ сущности и свойств тригонометрических и обратных тригонометрических функций. Характеристика основных методов решения элементарных тригонометрических уравнений, а также примеры решения нестандартных тригонометрических уравнений и неравенств.
курсовая работа, добавлен 09.11.2017
Способы решения уравнений, содержащих модуль. Использование геометрической интерпритации модуля для решения уравнений. Графики простейших функций, содержащих знак абсолютной величины. Доказательство теорем, определение, решение нестандартных уравнений.
реферат, добавлен 06.03.2010
Рассмотрение основных свойств и графиков обратных тригонометрических функций. Существенные принципы преобразования выражений, содержащих эти функции. Обзор исторической справки. Изучение примеров решения уравнений. Задание различного уровня сложности.
презентация, добавлен 04.12.2014
Основные тригонометрические тождества: формулы привидения, сложения, двойного и половинного угла, преобразования сумм тригонометрических функций в произведение. Графики и свойства обратных тригонометрических функций. Методы решения уравнений, неравенств.
контрольная работа, добавлен 16.06.2010
Средние величины, неравенство Коши. Доказательство неравенств методами «от противного» и математической индукции. Использование неравенства Коши-Буняковского при решении тригонометрических уравнений. Решение уравнений с помощью замечательных неравенств.
курсовая работа, добавлен 23.10.2017
Преобразование и объединение групп общих решений тригонометрических уравнений. Решение уравнений с применением формул тройного аргумента или понижения степени. Функциональные методы решения тригонометрических и комбинированных уравнений, отбор корней.
реферат, добавлен 09.09.2016
Преобразование графиков тригонометрических функций путем параллельного переноса, сжатия и расширения. Анализ промежутков монотонности функции. Точки экстремума. Формирование навыков решения и построения тригонометрических уравнений и неравенств.
презентация, добавлен 02.05.2012
Равносильность уравнений с параметрами. Теоремы о равносильных преобразованиях уравнений, их доказательство и следствие. Характеристика равносильности неравенств с параметрами, их основные теоремы, определение из лемм, доказательства и следствия.
лекция, добавлен 01.09.2017
Нестандартные приемы решения уравнений и неравенств, содержащих модуль, изучаемых на дополнительных занятиях и при решении олимпиадных задач. Типовые задания на решение уравнений и неравенств. Задания тестовых вариантов Единого Национального Тестирования.
дипломная работа, добавлен 12.11.2014
Действия с комплексными числами. Системы линейных уравнений с тремя неизвестными. Решение линейных неравенств, содержащих знак модуля. Показательная функция, ее свойства, график. Показательные уравнения и неравенства. Логарифмическая функция, ее свойства.