Прямоугольный треугольник

«Решение задач на построение треугольников».

Предмет: Геометрия

Класс: 7

Тема: Решение задач на построение треугольников.

Цель: закрепить в процессе решения задач усвоение изученного материала по теме «Прямоугольные треугольники», продолжить формирование навыков в решении задач на построение.

Планируемые результаты: Предметные: Решают задачи на вычисление, доказательство и построение, проводят по ходу решения дополнительные построения. Метапредметные: Строят логически обоснованное рассуждение, включающее установление причинно-следственных связей. Применяют установленные правила в планировании способа решения. Приводят аргументы в пользу своей точки зрения, подтверждают ее фактами. Личностные: Проявляют мотивацию к познавательной деятельности при решении задач с практическим содержанием.

Оборудование: учебник Геометрия 7-9 кл. Л.С. Атанасян, карточки, классная доска, мел, демонстрационные чертежные инструменты (линейка, циркуль).

Ход урока:

I.  Организационный этап. Приветствие, подготовка к уроку.

II. Актуализация опорных знаний.

Анализ результатов самостоятельной работы.

Проверка д/з: вопросы 14, 15, 16, 18, 20 на с. 89 письменно; решить № 291 г,д, № 293).

Далее: Разобрать задачу № 293. Решение задачи № 293 приведено в учебнике на с. 88-89. (Желающие работают у доски)

III. Закрепление изученного материала.

Решить задачу на построение: Построить прямоугольный треугольник по гипотенузе и внешнему углу при вершине острого угла.

Решение:

Начертим данные отрезок PQ и угол hk.

Построение:

1) Проведем прямую, отметим на ней точку В и отложим отрезок ВС, равный PQ.

2) Отложим от луча ВД, являющегося продолжением луча ВС, угол ДВМ, равный углу hk.

3) Построим прямую, проходящую через точку С и перпендикулярную к прямой ВМ, и обозначим буквой А точку пересечения этой прямой с лучом ВМ. Треугольник ABC искомый.

Доказательство (устно):

По построению треугольник ABC — прямоугольный, гипотенуза ВС равна данному отрезку PQ и внешний угол АВД треугольника равен данному углу hk. Таким образом, построенный треугольник ABC удовлетворяет всем условиям задачи.

Указание: задача имеет решение только в том случае, когда данный угол hk тупой. Желательно, чтобы учащиеся сами обосновали справедливость этого утверждения.

 3

 IV. Самостоятельная работа.

Вариант I

1. Постройте прямоугольный треугольник по гипотенузе и прилежащему острому углу.

Вариант II

1. Постройте равнобедренный треугольник по основанию и медиане, проведенной к основанию.

VI. Итоги урока. Рефлексия.

VII. Домашнее задание: пункт 33-39 повторить; решить задачи № 294, 301, 314 (б,в).

Доп-но № 315 (на выбор)



Решение задач по теме «Треугольники» (7-й класс)

Разделы: Математика

Класс: 7

Цели и задачи урока:

• обобщить, закрепить и углубить знания по изученной теме;
• формировать умение обучаемых доказывать равенство данных треугольников, опираясь на изученные признаки, применять свойства равнобедренного треугольника;
• отработать навыки решения простейших задач на построение с помощью циркуля и линейки;

развивать логическое мышление, самостоятельность учащихся при решении заданий; умение на практике применять знания, полученные на уроках;

воспитывать познавательную активность, упорство в достижении поставленной цели, культуру умственного труда

Оборудование:

• интерактивная доска или наглядный материал (готовые чертежи);
• карточки с задачами для индивидуальной работы на доске;
• таблицы с признаками равенства треугольников.

Тип урока: урок закрепления полученных знаний.

Ход урока

І. Организационный момент.

Учитель:

— Тема урока: «Решение задач по теме «Треугольники»». Мы сегодня обобщим и систематизируем знания по данной теме и наша цель: подготовиться к контрольной работе, которая будет на следующем уроке.

— Откройте дневники и запишите домашнее задание.

• I уровень: № 120(б), 121;
• II – III уровень: №160 (б), 162(б).

II. Актуализация опорных знаний.

1. У доски двое учащихся решают задачи по карточкам.

Начертите равнобедренный треугольник АВС с основанием АС. С помощью циркуля и линейки проведите медиану АА1 к боковой стороне ВС.

Дано: АО = BO, СО = DO, CO = 5см, ВО = 3см, BD = 4см. 1)Докажите, что

2. Для остальных учащихся класса организована фронтальная работа.

Цель: повторить основные вопросы теории темы «Равнобедренный треугольник и его свойства» с помощью теста. (Вопросы теста – на интерактивной доске)

Теоретический тест. В каждом задании из трёх предложенных ответов выберите верный и обоснуйте его. Верных ответов может быть несколько. Подумайте и ответьте на вопрос. (А я считаю, что…; я не согласна с этим утверждением, т.к. …)

1) Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение: а) всегда верно; б) может быть верно; в) всегда неверно. Ответ: б), если медиана проведена к основанию равнобедренного треугольника.

2) Если треугольник равносторонний, то: а) он равнобедренный; б) все его углы равны; в) любая его высота является биссектрисой и медианой. Ответ: а), б), и в), равносторонний треугольник является частным случаем равнобедренного треугольника; в равнобедренном треугольнике углы при основании равны, поэтому в равностороннем треугольнике все углы равны.

3) В каком треугольнике только одна его высота делит треугольник на два равных треугольника? а) в любом; б) в равнобедренном; в) в равностороннем. Ответ: б), высота, проведённая к основанию равнобедренного треугольника.

4) Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение: а) всегда верно; б) может быть верно; в) всегда неверно. Ответ: а)

5) Если треугольник равнобедренный, то а) он равносторонний; б) любая его медиана является биссектрисой и высотой; в) ответы а) и б) неверны. Ответ: в), т.к. равнобедренный треугольник не всегда является равносторонним; медиана, проведённая к боковой стороне равнобедренного треугольника, не является биссектрисой и высотой, если треугольник не равносторонний.

6) В каком треугольнике любая его высота делит треугольник на два равных треугольника? а) в любом; б) в равнобедренном; в) в равностороннем. Ответ: в).

Учитель: — Мы с вами повторили материал темы «Равнобедренный треугольник и его свойства», а теперь повторим признаки равенства треугольников

(Обратить внимание обучающихся на таблицы с признаками равенства треугольников). 3. Задачи в рисунках (на интерактивной доске)

Задачи в рисунках (на интерактивной доске)

3. Задачи в рисунках (на интерактивной доске).

Учитель: — Определите, являются ли равными треугольники на рисунках.

— Сколько пар равных элементов должно быть в равных треугольниках?

Идеальные объекты

Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.

Все эти фигуры обладают двумя свойствами:

• симметрия
• равенство или подобие составных частей.

Равенство частей можно заметить у квадрата, ромба или равностороннего треугольника — равенство сторон. Также у них есть одна или несколько линий симметрии.

У шара бесконечное количество осей симметрии и плоскостей симметрии, но отсутствует равенство или подобие составных частей.

Все типы правильных многогранников обладают симметрией, при этом составлены из некоторого количества одинаковых фигур (треугольников, квадратов, пятиугольников).

Из всего этого можно сделать вывод, что отличить правильную геометрическую фигуру от произвольной совсем не сложно. Достаточно выяснить, имеет ли данная фигура оси или плоскости симметрии, а также из каких повторяющихся частей она состоит.

Таким образом, именно по наличию или отсутствию симметрии и равенства или подобия составных частей можно оценивать различные объекты окружающего мира на соответствие правильному геометрическому виду.

Например, возьмем два треугольника. На первый взгляд, они похожи, но у одного из них одна сторона вогнутая, вторая — выпуклая. А у другого наоборот.

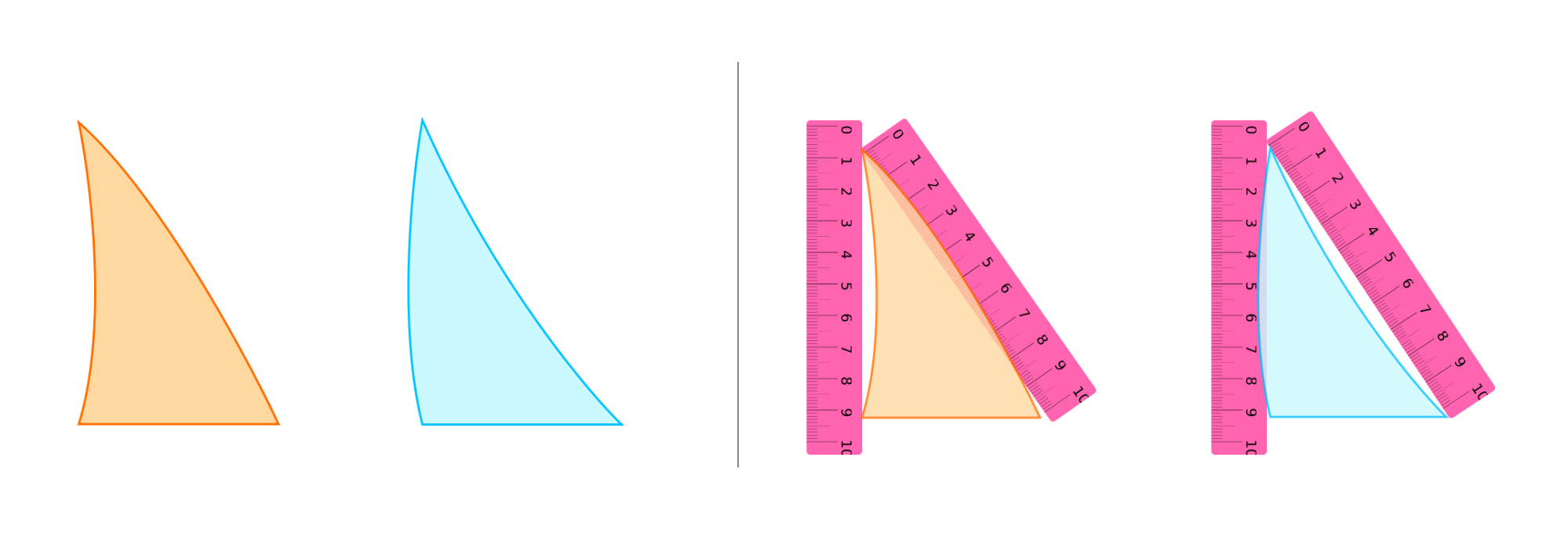
Математика занимается идеальными объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.

Например, теорема Пифагора звучит так: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. А затем это свойство можно применять при решении задач и составлении чертежей.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Геометрические теоремы в оригами

Теорема 1: Сумма углов любого треугольника равна 180 градусов.

Доказательство.

1. Возьмем лист бумаги, имеющий форму произвольного треугольника.

3. Совместим вершины треугольника с точкой у основания высоты треугольника (Приложение 4).

Теорема 2. Накрест лежащие углы, образованные при пересечении двух параллельных прямых секущей, равны.

Доказательство:

1. Возьмем лист бумаги с двумя параллельными сторонами и секущей АВ.

2. Совместим вершины накрест лежащих углов- точки А и В.

3.Углы 1 и 2 совпали при наложении, следовательно, угол 1 равен углу 2. Значит, накрест лежащие углы, образованные при пересечении двух параллельных прямых секущей, равны (Приложение 5).

Теорема 3.

Доказательство:

1.Возьмем квадратный лист бумаги и наметим на нем середину стороны.

2.Точка D должна лечь на намеченную линию.

3.Согнем по указанной линии, а потом отогнем угол в первоначальное положение.

4.Теперь точку А положим на намеченную линию.

5.Опять отогнем линию и вернем в первоначальное положение (Приложение 6).

Продолжая рассматривать задачи, возникает следующий вопрос: «Многие ли учащиеся знают такой способ решения?». Для этого был проведен опрос учащихся 7-9 классов (Приложение 7).

Количество опрошенных: 7 классы – 89 человек, 8 классы- 45 человек, 9 классы- 80 человек. Опрос показал, что большая часть учащихся не знают, что существует такой способ решения геометрических задач как оригами, однако многие хотели бы его рассмотреть (Приложение 8).

Результаты анкетирования побудили к созданию серии фрагментов «Наглядная геометрия своими руками» и так как это дополнительный материал необходимый не только для изучения, но и для повторения в ходе самообразования и подготовки к экзаменам, то возникла необходимость искать новую форму подачи этого материала.

Форма изложения должна быть не только интересной и наглядной, но и доступной в любое время и в любом месте, так и появилась идея рождения серии видео инструкций по доказательству и решению задач с помощью оригами.

Кроме создания видео инструкций по доказательству и решению задач геометрии 7-9 класс с помощью оригами, по нашему мнению было бы интересно создать и серию видео инструкций по работе с оригами как внеклассную работу по пропедевтики геометрии 5-6 класс.

Заключение

Подводя итог выполненной работы, можно отметить, что оригами, как одно из направлений искусства, является наиболее логичной и гармоничной формой изучения геометрии, выступая как наглядное и практическое средство подтверждения логических рассуждений.

Исследуя различные классы задач, понимаешь, что оригами уже само по своей природе является целым разделом геометрии, с помощью которого можно изучать и исследовать геометрические фигуры и понятия, а главное способствовать развитию пространственного воображения и творческого мышления.

На мой взгляд математика – является одной из сторон искусства оригами, при этом оригами является одним из способов изучения и понимания математики.

В заключении необходимо отметить, что проделанная работа может принести пользу не только в изучении геометрии, но при подготовке к экзаменам и самообразованию, а созданные видео инструкции представят интерес и для родителей, учителей как помощник. Для меня же данный проект являлся отправной точкой в изучении различных способов быстрого, наглядного решения геометрических задач.

Список литературы

1. Афонькин С. Ю., Афонькина Е. Ю. Энциклопедия оригами. — СПб.: ООО Издательский дом «Кристалл», 2000.
2. Афонькин С.Ю., Афонькина Е.Ю. Все об оригами/Справочник. С-Пб: изд.Кристалл, М: «Оникс», 2005.
3. О. В. Весновская. Оригами: орнаменты, кусудамы, многогранники. -Чеб.: изд. «Руссика», 2003г.
4. С. Н. Белим. Задачи по геометрии, решаемые методами оригами. – М.: изд. «Аким», 1998г.
5. Интернет

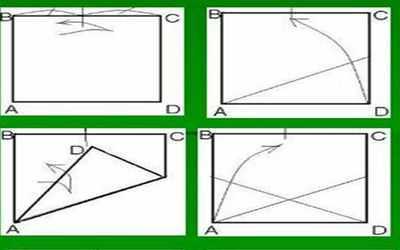
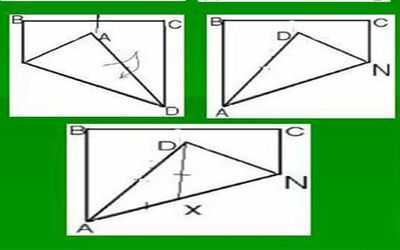
Приложение 4. Анкета для учащихся 7-9 классов

1. Трудно Вам выполнять наглядное представление геометрических задач при решении?
2. Знаете ли Вы, что некоторые задачи по геометрии можно решать с помощью обычного перегибания листа бумаги (оригами)?
3. Хотели бы вы совместить свои знания в геометрии с техникой оригами для упрощения изучения геометрии?
4. Если в Internet будут предложены такие задачи, Вы будете обращаться к этому ресурсу и как часто?

Приложение 5. Результаты анкетирования

Диаграмма 1. Процент трудности в наглядном представлении геометрических задач

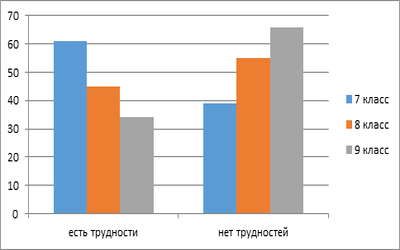
Диаграмма 2. Знаете ли Вы способ решения геометрических задач — оригами?

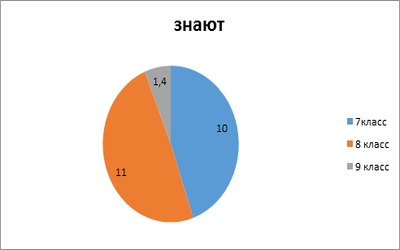
Диаграмма 3. Хотели бы вы совместить свои знания в геометрии с техникой оригами для упрощения изучения геометрии?

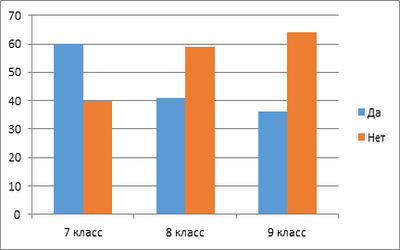
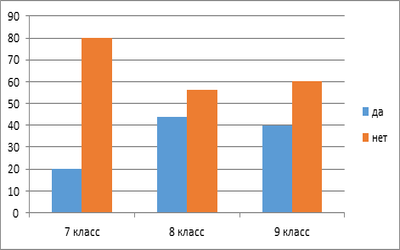
Диаграмма 4. Вы будете обращаться к этому ресурсу?

Свойства прямоугольного треугольника

Прямоугольный треугольник — это симметричный многоугольник, сумма двух углов которого равняется 90 градусов. Так как общая сумма всех трёх углов составляет 180 градусов, то соответственно третий угол равен 90 градусам. Стороны, образующие его, называют катетами, а оставшийся отрезок гипотенузой.

К основным свойствам фигуры относят следующее:

• гипотенуза многоугольника всегда больше любого из его катетов;
• сторона, располагающаяся напротив угла в 30 градусов, составляет половину гипотенузы;
• два катета являются высотами треугольника;
• середина окружности, описанная вокруг фигуры, совпадает с гипотенузой, при этом медиана, опущенная из прямого угла на гипотенузу, одинаковая с радиусом круга;
• численное значение гипотенузы, возведённое в квадрат, равно сумме квадратов катетов (теорема Пифагора).

Так, если известна гипотенуза, то найти катеты, зная угол, не составит труда. Определив же длину катетов, вычислить оставшуюся сторону можно по теореме Пифагора. Периметр фигуры определяют сложением двух катетов и гипотенузы, а площадь находят перемножением катетов и делением полученного ответа на два.

Зная катеты, довольно просто вычислить угол. Нужно всего лишь запомнить, что соотношение сторон между собой равно тангенсу противолежащего угла и котангенсу, находящемуся рядом. При этом, зная любой из углов, найти второй можно простым вычитанием известного значения из девяноста. Высота же у прямоугольника равна косинусу прилежащего угла.

Формула для нахождения биссектрисы и медианы довольно сложная. Для нахождения первой величины используют преобразование радикала из суммы квадратов катетов к двум, а второй — подстановку радикала вместо стороны, лежащей напротив прямого угла.

Признаки равенства прямоугольных треугольников

1. По двум катетам: Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.
2. По катету и гипотенузе: Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
3. По гипотенузе и острому углу: Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольникиравны.
4. По катету и острому углу: Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.

7 класс геометрия сложная тема, разъяснить подробно для детей

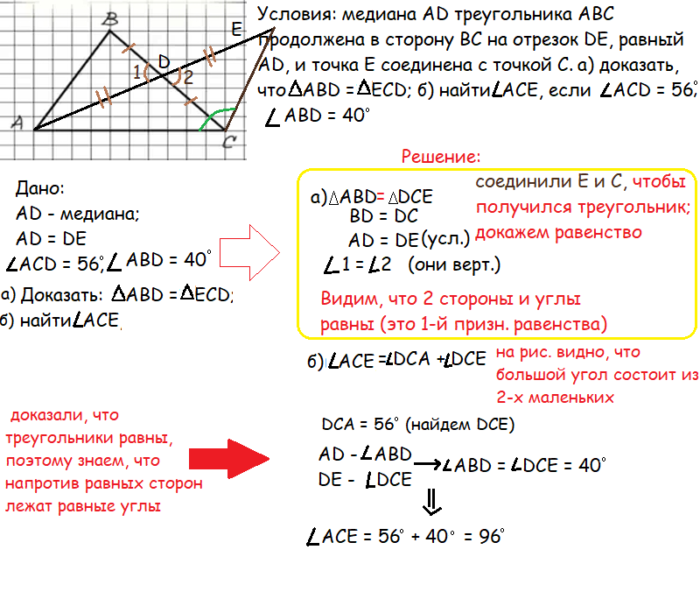
Решим более сложную задачу, где есть и доказательство равенства треугольников, и поиск углов. Алгоритм решения задачи:

Шаг 1. Начертим, согласно условиям. Дается треугольник АВС, в котором провели медиану (вспоминаем, что медиана делит  сторону пополам). В нашей задаче медиана AD уходит за пределы треугольника, создавая дополнительный отрезок DE (он равен AD). Получился треугольник, из которого проведена медиана.

Шаг 2. Первая задача — доказать равенство треугольников ABD и ECD: соединим точку Е и С, чтобы получился треугольник.

Шаг 3. По условиям AD и DE равны (одна сторона треугольника равна другой стороне ⇒ AD = DE

Шаг 4.  Получается BD = DC, так как медиана разделила BC пополам (выходит, еще одни стороны треугольников равны).

Шаг 5. Рассмотрим углы между сторонами (на рис. обозначены цифрами 1 и 2). Они вертикальные, так как образовались двумя прямыми. Следовательно, они равны.

Из первого признака равенства треугольников знаем, что если 2 стороны и угол между этими сторонами одного треугольника равен этим показателям во втором, то они равные. Пункт а доказан. Переходим к б.

Шаг 1. Нам нужно найти угол АСЕ. Из рисунка видно, что он состоит из 2-х маленьких углов, получается: угол АСЕ равен сумме углов DCA и DCE.

Шаг 2. По условиям мы знаем, чему равен DCA, осталось найти второй. Так как равенство треугольников доказали, значит воспользуемся правилом: напротив равных сторон треугольников лежат и равные углы. AD напротив ABD; DE напротив DCE. Выходит: угол ABD = углу DCE = 40 градусам (по условию).

Шаг 3. Маленькие углы известны, найдем тот, который требуется: угол ACE = 56º + 40º = 96º.

Равенство доказали, угол нашли. Задание выполнено.

Еще пара видеороликов про решение задачи с прямоугольным треугольником, а также вся геометрия за 7 класс в одной задаче.

Откладывание отрезка

Для откладывания отрезка, равного данному отрезку (рис. 296, а) на прямой (рис. 296, б), следует: 1) отметить на прямой точку М; 2) радиусом, равным а, провести дугу окружности с центром в точке М (сделать засечку на прямой ).

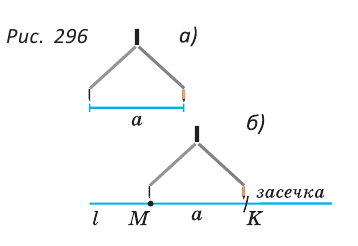
В пересечении дуги и прямой получим точку К и отрезок МК, равный .

Операция откладывания отрезка на прямой позволяет построить сумму и разность двух отрезков (рис. 297): в первом случае на произвольной прямой откладывают последовательно два отрезка, во втором — на большем отрезке от любого его конца откладывают меньший отрезок.

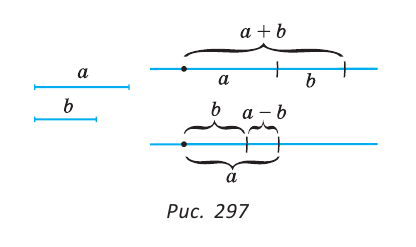
В дальнейшем при решении задач на построение мы не будем описывать процедуру откладывания отрезка на прямой, считая ее элементарной операцией.

Перечислим 5 основных задач на построение, к которым сводятся другие задачи. Решая сложные задачи, будем ссылаться на эти основные, не описывая ту часть решения, которая связана с одной из основных задач.

• Задача I. Построение треугольника по трем сторонам.
• Задача II. Построение угла, равного данному.
• Задача III. Построение биссектрисы угла.
• Задача IV. Построение середины отрезка.
• Задача V. Построение прямой, перпендикулярной данной.

В некотором смысле «линейка» и «циркуль» — это два идеальных робота, которые могут выполнять определенный набор операций. И наша задача — составить алгоритм из последовательности таких операций — команд для этих роботов, который приведет к построению необходимой фигуры. Фактически нужно написать программу для «циркуля» и «линейки».

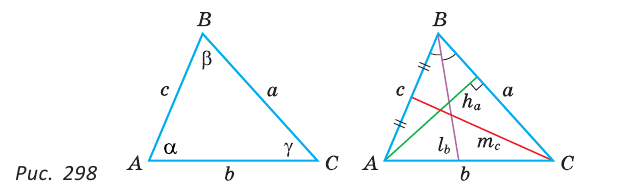
Замечание. В треугольнике ABC стороны, противолежащие углам А, В и С, будем соответственно обозначать , и , а сами эти углы — , и (рис. 298). Медианы, проведенные к сторонам , и , — высоты — биссектрисы —

Треугольник

Треугольник в геометрии представляет одну из основных фигур. Из предыдущих уроков вы знаете, что треугольник – это многоугольная фигура, которая имеет три угла и три стороны.

Задание

• Вспомните и ответьте, что является вершинами треугольника?
• Какие разновидности треугольников вы можете назвать?
• Какая отличительная черта разных видов треугольников?
• Что называется катетом прямоугольного треугольника?
• Дайте определение катетам данного треугольника.
• Какой треугольник называется тупоугольным?
• Охарактеризуйте остроугольный многоугольник.
• Что значит косоугольный треугольник?

Из истории математики

Изображения треугольников и задачи с их применением можно найти на папирусах, найденных в Древней Греции и Египте. Древние мудрецы для облегчения задач стали применять определенные знаки, обозначая ими геометрические фигуры. Так еще в первом веке Герон вместо слов стал использовать треугольник.

Немного позже эта геометрическая фигура одной из первых появилась в изображении орнаментов древних цивилизаций.

Даже в Вавилонской геометрии, такая фигура, как прямоугольный треугольник занимала очень важное и почетное место. Впервые о нем упоминается в папирусе Ахмеса.. Среди этих прямоугольных треугольников широкое значение имеет египетский треугольник

Что же это за такой египетский треугольник? Оказывается, в египетской архитектуре для построения прямых углов применялось такое соотношение сторон, как 3:4:5. Само название «египетский треугольник» появилось очень давно, вероятно еще в V веке до н.э. Это название произошло именно из Древнего Египта, так местное население широко применяло такой тип треугольника в повседневной жизни и различных сферах деятельности.

Среди этих прямоугольных треугольников широкое значение имеет египетский треугольник. Что же это за такой египетский треугольник? Оказывается, в египетской архитектуре для построения прямых углов применялось такое соотношение сторон, как 3:4:5. Само название «египетский треугольник» появилось очень давно, вероятно еще в V веке до н.э. Это название произошло именно из Древнего Египта, так местное население широко применяло такой тип треугольника в повседневной жизни и различных сферах деятельности.

Архитекторы и землемеры того времени, чтобы построить прямой угол использовали веревку, которую делили узлами или отметками на двенадцать частей, то есть три плюс четыре и плюс пять. Такой своеобразный треугольник образовывался благодаря натяжению шнура и показывал весьма точную прямоугольную форму, в котором катеты играли роль направляющих для использования в кладке прямого угла нужного сооружения. Благодаря такому изобретению, египетские строители теперь могли более точно делать расчеты для разметки земли под хозяйственные работы и применять их при строительстве пирамид.

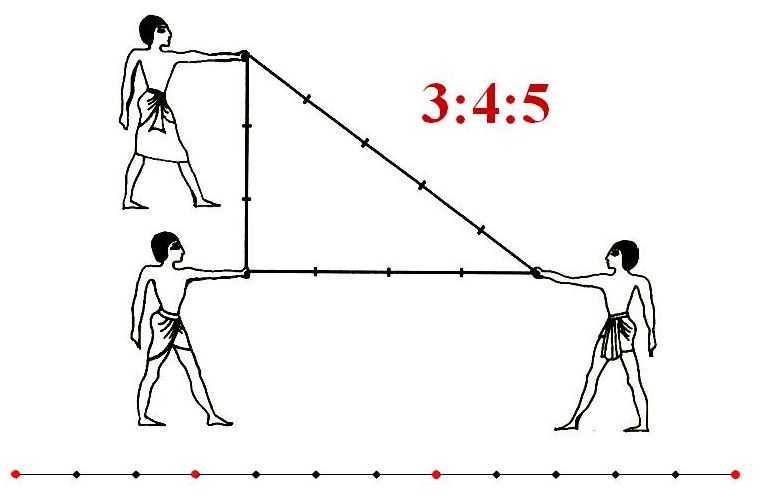
Египетский треугольник так же имеет некоторые отличительный особенности. Например, все его стороны и площадь представляю собой целый числа, из-за его прямоугольности он активно применяется в строительстве для отмерения прямых углов. К тому этот уникальный треугольник легко строиться с помощью обыкновенной веревки, как изображено на рисунке.

Но самым важным в феномене египетского треугольника было то, что именно его необычные свойства подтолкнули Пифагора к попытке обобщить каким-то образом все другие прямоугольные треугольники, что и стало в итоге известно под названием теоремы Пифагора!

Задание: Где еще в повседневной жизни можно встретить треугольник?

Решение задач по теме «Прямоугольные треугольники» (7 класс)

МУНИЦИПАЛЬНОЕ КАЗЕННОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ СУЗУНСКОГО РАЙОНА

« СУЗУНСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 301

им. В.А. ЛЕВИНА»

633621, Новосибирская область, Сузунский район, р.п. Сузун,

Учитель математики

Панасюк Жанна Петровна

2017 год

Решение задач по теме «Прямоугольные треугольники» (2сл.)

Цели урока:

1. Закрепить основные свойства прямоугольных треугольников.

2. Совершенствовать навыки применения основных свойств прямоугольных треугольников при решении задач.

3. Развивающая – развивать самостоятельность и мышление ребенка средствами своего предмета.

4. воспитательная – воспитывать стремление к познанию окружающего мира, настойчивость в достижении конечных результатов своей деятельности.

Задачи, решаемые на уроке:

1. научить учащихся самостоятельно работать;

2. высказывать предположения и догадки;

3. уметь делать обобщение изучаемых факторов.

Оборудование: доска, мел, мультимедийный проектор, раздаточный материал

Хронометраж урока.

1. Определение темы урока совместно с учащимися – 1мин.

2. Определение целей и задач урока совместно с учащимися – 2мин.

3. Актуализация знаний (фронтальный опрос) – 5мин.

4. Пауза –релаксация.

5. Устная работа «Решение задач по готовым чертежам» — 7мин.

6. Работа с учебником, решение задачи вместе с классом с оформлением решения (с учеником у доски) – 7мин.

7. Физминутка.

8. Самостоятельная работа (дифференцированная) с взаимопроверкой и самопроверкой – 7мин.

9. Подведение итогов урока, установление обратной связи – 3мин.

10. Задание на дом – 1мин.

Итого 40 минут.

Ход урока.

1. Орг. момент (1мин).

Записываем тему урока. (2 сл.)

2. Определение целей и задач урока совместно с учащимися (2мин).

Давайте скажем чем же мы сегодня на уроке будем заниматься?

Учитель при помощи учащихся формулирует и проговаривает цели и задачи данного урока. Мы с вами работаем с контрольными листами.

3. Актуализация знаний (фронтальный опрос – 5мин). (3 сл.)

1. Какой треугольник называется прямоугольным?

2. Как называются стороны прямоугольного треугольника?

3. Сформулируйте теорему о сумме углов треугольника.

4. Какой угол называется внешним углом треугольника?

5. Чему равен внешний угол треугольника?

6. Сформулируйте свойства прямоугольных треугольников.

1.Сумма двух острых углов прямоугольного треугольника равна 90.

2.Катет прямоугольного треугольника лежащий против угла в 30, равен половине гипотенузы.

3.Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30.

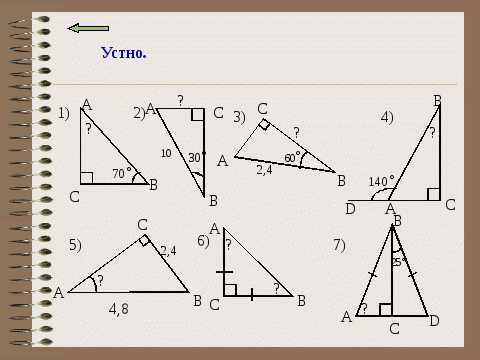
4. Устная работа «Решение задач по готовым чертежам» (7мин). (4 сл.)

Учащиеся, увидев задачу, решают её самостоятельно. Ответ фиксируют в оценочном листе. Затем решение разбирается всем классом, и ученик проверяет правильность своего решения.

Физминутка (5 сл.)

В стране Геометрия очень важно уметь смотреть и видеть, замечать и отмечать различные особенности геометрических фигур:

Кто ничего не замечает,

Тот ничего не изучает!

Кто ничего не изучает –

Тот вечно хнычет и скучает!

5. Самостоятельная работа (дифференцированная) с взаимопроверкой и самопроверкой (7мин).

Учащиеся работают по своей карточке, затем меняются и проверяют друг друга. После на доске показывается верное решение и ответы и учащиеся оценивают свою работу, фиксируя результаты в оценочном листе.

Ответы. (6 сл.)

(Легкий уровень сложности – «3») (7 сл.)

(Средний уровень сложности – «4») (8 сл.)

(Высокий уровень сложности – «5») (9 сл.)

6. Решение задачи вместе с классом с оформлением решения (с учеником у доски -7мин). (10 сл.)

Задача. Для изготовления праздничного колпака в форме перевернутого конуса нужно узнать площадь поверхности колпака по формуле S = Пrl (П ≈3). ВАС = 60, l = 34см. Найдите площадь поверхности колпака.

Решение. 1) Так как ВАС = 60, то по свойству прямоугольного треугольника АВО = 30.

2) Значит, r = ∙l, r = ∙ 34 = 17 (см).

3) S = Пrl, S = 3∙17∙34 =2034 (см2)

Ответ.2034см2 .

Задача №258 (работа с учебником, резервная).

Дано: АВС – равносторонний, АВ = 12см, D – середина стороны ВС, DМ – перпендикуляр к прямой АС.

Найти: АМ — ?

Решение. 1) Так как треугольник АВС равносторонний, то все углы у него по 60.

2) Так как DМ – перпендикуляр, то по свойству прямоугольного треугольника СDМ = 30.

3) Так как D – середина ВС, то DC = 6см.

4) По свойству прямоугольного треугольника МС = 3см.

5) Значит АМ = АС – МС = 12 – 3 = 8см.

Ответ. 8см.

7. Подведение итогов урока, установление обратной связи,

задание на дом (3мин).

Поднимите руку у кого от 15 – 20 б. — «5»

от 10 – 14 б. – «4»

от 5 – 10 б. – «3»

< 5 б. – нужно ещё работать.

8. Задание на дом (с комментариями – 1 мин).

Устно: повторить п.31-36

Письменно: №265 с. 81 Чертёж на доске.

Рефлексия.

Спасибо вам за урок.

Урок окончен. До свидания!

(Легкий уровень сложности – «3»)

(Средний уровень сложности – «4»)

(Высокий уровень сложности – «5»)