Равнобедренный треугольник. онлайн калькулятор

Признаки равнобедренного треугольника

Если два угла треугольника равны, то треугольник равнобедренный.
Если медиана треугольника является его высотой, то треугольник равнобедренный.
Если биссектриса треугольника является его высотой, то треугольник равнобедренный.
Если медиана треугольника является его биссектрисой, то треугольник равнобедренный.

Первый способ.

Поскольку $\angle B$ и $\angle C$ острые (иначе сумма углов
треугольника $ABC$ была бы больше $180^\circ$), то высота,
проведенная из вершины $A$ падает на сторону $BC$.

Так как сумма углов треугольника равна $180^\circ$, то $\angle 1=180^\circ-90^\circ-\angle B=180^\circ-90^\circ-\angle C=\angle 2$.

Следовательно, треугольники $ABD$ и $ACD$ равны по второму признаку равенства треугольников $(\angle 1=\angle 2, \angle 3=\angle 4, AD$– общая сторона$)$.

Тогда $AB=AC$, то есть треугольник равнобедренный.

Второй способ.

Если предположить, что одна из указанных сторон больше другой, то угол, лежащий против нее, будет больше угла, лежащего против другой стороны, а это противоречит условию (тому, что данные углы равны).

Итак $AB=AC$.

Докажем второй пункт теоремы

Докажем теперь, что если $AD$ – медиана и высота, то треугольник равнобедренный.

Действительно, так как $BD=DC, \angle 3=\angle 4=90^\circ$, a $AD$ – общая сторона, то треугольники $ABD$
и $ACD$ равны по первому признаку равенства треугольников.

Следовательно, $AB=AC$, то есть треугольник равнобедренный.

Докажем третий пункт теоремы

Докажем, что если $AD$ – биссектриса и высота для $\triangle ABС$, то треугольник равнобедренный.

Действительно, так как $\angle 1 =\angle 2, \angle 3=\angle 4=90^\circ$, a $AD$ – общая сторона, то
треугольники $ABD$ и $ACD$ равны по второму признаку равенства треугольников.

Следовательно, $AB=AC$, то есть треугольник равнобедренный.

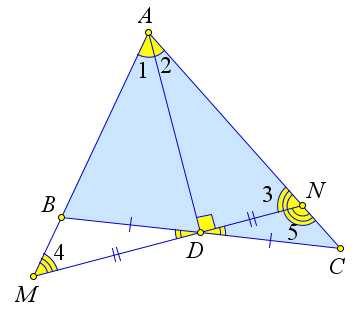
Докажем четвертый пункт теоремы

Докажем, что если $AD$ – медиана и биссектриса, то треугольник
равнобедренный.

Предположим противное – треугольник $ABC$ не равнобедренный, и, следовательно, $AD$ не
высота.

Проведем через точку $D$ прямую $l$ перпендикулярно $AD$.

Обозначим точки пересечения прямой $l$ с прямыми $AB$ и $AC$ как $M$
и $N$ соответственно.

Треугольник $AMN$ – равнобедренный, так как $AD$ – биссектриса и высота этого треугольника.

Тогда $AD$ – медиана треугольника $AMN$, то есть $MD=ND$.

Тогда треугольники $BMD$ и $CND$ равны по первому признаку $(\angle BDM=\angle CDN$ как
вертикальные, $BD=DC, MD=ND)$.

Тогда $\angle 4=\angle 5$, и, следовательно, прямые $AB$ и $AC$ параллельны, что невозможно.

Доказательство равенства треугольников

Посмотри внимательно, у нас есть:

$ \displaystyle \underbrace{AB}_{гипотенуза \ в\ \Delta ABH}=\underbrace{BC}_{гипотенуза\ в\ \Delta СBH}$
$ \displaystyle BH\text{ }=\text{ }BH$ (ещё говорят, $ \displaystyle BH$— общая)

И, значит, $ \displaystyle AH\text{ }=\text{ }CH$!

Почему?

Да мы просто найдём и $ \displaystyle AH$, и $ \displaystyle CH$ из теоремы Пифагора (помня ещё при этом, что $ \displaystyle AB=BC$)$ \displaystyle AH=\sqrt{A{{B}^{2}}-B{{H}^{2}}}$$ \displaystyle CH=\sqrt{B{{C}^{2}}-B{{H}^{2}}}$

Удостоверились? Ну вот, теперь у нас$ \displaystyle \begin{array}{l}AB=BC\\BH=BH\\AH=CH\end{array}$А уж по трём сторонам – самый легкий (третий) признак равенства треугольников.

Ну вот, наш равнобедренный треугольник разделился на два одинаковых прямоугольных.

Отметим на картинке все одинаковые элементы (углы и стороны).

Видишь, как интересно? Получилось, что:

В равнобедренном треугольнике углы при основании равны: $ \displaystyle \angle A=\angle C$;
Высота, проведенная к основанию $ \displaystyle (ВH)$, совпадает с медианой и биссектрисой
$ \displaystyle AH=CH$
$ \displaystyle \angle 1=\angle 2$.

Вспоминаем тут, что медиана – линия, проведённая из вершины, которая делит сторону пополам, а биссектриса – делит угол.)

Ну вот, здесь мы обсудили, что хорошего можно увидеть, если дан равнобедренный треугольник.

И теперь возникает другой вопрос: а как узнать, равнобедренный ли треугольник?

Другие свойства равнобедренного треугольника

Положение центра окружности, описанной вокруг равнобедренного треугольника, зависит от величины угла вершины. Так, если равнобедренный треугольник остроугольный, центр круга располагается внутри фигуры.

Центр окружности, которая описана вокруг тупоугольного равнобедренного треугольника, лежит вне его. И, наконец, если величина угла при вершине равна 90°, центр лежит ровно на середине основания, а через само основание проходит диаметр окружности.

Для того чтобы определить радиус окружности, описанной около равнобедренного треугольника, достаточно разделить длину боковой стороны на удвоенный косинус половины величины угла при вершине.

Какими бывают треугольники

Обычный разносторонний треугольник — это замкнутая геометрическая фигура, состоящая из трёх отрезков разной длины и трёх углов, ни один из которых не является прямым. Кроме него, различают несколько особых видов.

Треугольник остроугольный имеет все углы величиной менее 90 градусов. Иными словами — все углы такого треугольника острые.

Прямоугольный треугольник, над которым во все времена плакали школьники из-за обилия теорем, имеет один угол с величиной 90 градусов или, как его ещё называют, прямой.

Тупоугольный треугольник отличается тем, что один из его углов тупой, то есть величина его — более 90 градусов.

Равносторонний треугольник имеет три стороны одинаковой длины. У такой фигуры равны также все углы.

И наконец, у равнобедренного треугольника из трёх сторон две равны между собой.

Связь между биссектрисой и медианой

Любая биссектриса равнобедренного треугольника является его медианой. Это связано с особенностями равнобедренных треугольников и их внутренних углов.

Биссектриса — это отрезок, который делит угол на две равные части. В случае равнобедренного треугольника, у него есть две биссектрисы, каждая из которых делит угол при основании на две равные части.

Медиана — это отрезок, который соединяет вершину треугольника с серединой противоположной стороны. В случае равнобедренного треугольника, медиана соединяет вершину с серединой основания.

Заметим, что в равнобедренном треугольнике все стороны и углы одинаковы, поэтому все биссектрисы будут равными и делят соответствующие углы пополам. Также все медианы будут равными, так как каждая проходит через середину соответствующей стороны.

Таким образом, любая биссектриса равнобедренного треугольника является его медианой. Эта связь является одним из свойств равнобедренных треугольников и может быть использована для нахождения медианы, зная только биссектрису.

Определение медианы

Медиана — одна из важных характеристик треугольника, которая проходит из вершины до середины противоположной стороны. В отличие от биссектрисы, медиана не делит угол на две равные части.

Для любого треугольника, включая равнобедренный, любая из биссектрис является медианой. Это свойство позволяет использовать биссектрису для определения медианы, что упрощает решение некоторых задач.

Медиана треугольника делит стороны в отношении 2:1, то есть отношение отрезков, на которые медиана делит сторону, равно 2:1. Она также проходит через центр тяжести треугольника, где пересекает две другие медианы.

Медианы треугольника имеют множество применений. Они используются, например, для нахождения центра окружности, описанной вокруг треугольника, или для определения точки пересечения медиан, из которой можно провести прямую, делящую треугольник на две равные площади.

В равнобедренном треугольнике, где две стороны равны, медиана является высотой. Она проходит через вершину и перпендикулярна основанию треугольника.

Медиана треугольника является важным понятием в геометрии. Она представляет собой линию, которая проходит через вершину треугольника и точку, которая является серединой противоположной стороны. В случае равнобедренного треугольника, любая биссектриса также является его медианой.

Равнобедренный треугольник — это треугольник, у которого две стороны равны. В таком треугольнике медиана будет проходить через вершину и точку, которая делит основание на две равные части. Однако, в случае любого треугольника, медиана всегда проходит через вершину и середину противоположной стороны.

Медианы имеют ряд интересных и важных свойств. Например, все три медианы в треугольнике пересекаются в одной точке, называемой центром тяжести. Этот центр является точкой равновесия треугольника и делит каждую медиану в отношении 2:1, где длина медианы, ведущей к вершине, дважды больше длины медианы, ведущей к середине противоположной стороны.

Свойства медианы и биссектрисы

Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой. В таком треугольнике каждая биссектриса, проведенная из вершины угла, делящая противоположную сторону на две равные части, является медианой.

Медиана – это отрезок, соединяющий одну из вершин равнобедренного треугольника с серединой противоположной стороны. Основное свойство медианы равнобедренного треугольника заключается в том, что она делит противоположную сторону на две равные части. Это означает, что отрезок медианы, соединяющий вершину угла с серединой стороны, имеет одинаковую длину с другим отрезком, проведенным из вершины угла к противоположному углу.

Биссектриса – это отрезок, который делит угол на две равные части и пересекается в одной точке с противоположной стороной треугольника. В случае равнобедренного треугольника, биссектриса, проведенная из вершины угла без равных сторон, является медианой. Таким образом, в равнобедренном треугольнике любая биссектриса является одновременно медианой.

Высота равнобедренного треугольника

Итак, провели высоту. Что же получилось?

Из одного равнобедренного треугольника получилось два прямоугольных.

Это уже хорошо, но так получится в любом, даже самом «кособедренном» треугольнике.

Смотри:

Тоже два прямоугольных….

Чем же отличается картинка для равнобедренного треугольника? Смотри ещё раз:

Видишь, два прямоугольных треугольника (Δ???????????? и Δ????????????) – одинаковые!

Или, как математики любят говорить? Равные!

Ну, во-первых, конечно, этим странным математикам мало просто видеть – нужно непременно доказывать. А то вдруг эти треугольники чуть-чуть разные, а мы будем считать их одинаковыми.

Но не переживай: в данном случае доказывать почти так же просто, как и видеть.

Начнём?