Разность квадратов, сумма кубов и разность кубов

Доказательство формулы

Арифметическое

Давайте проверим формулу от обратного, т. е. перемножим (a-b) и (a+b) .

Раскрыв скобки с учетом правил арифметики получаем исходную формулу:
(a-b)(a+b) = a 2 + ab – ba – b 2 = a 2 – b 2 .

Геометрическое

Изобразим квадрат с длиной стороны a, площадь которого равна a 2 . В нем расположен квадрат поменьше со стороной b и площадью b 2 .

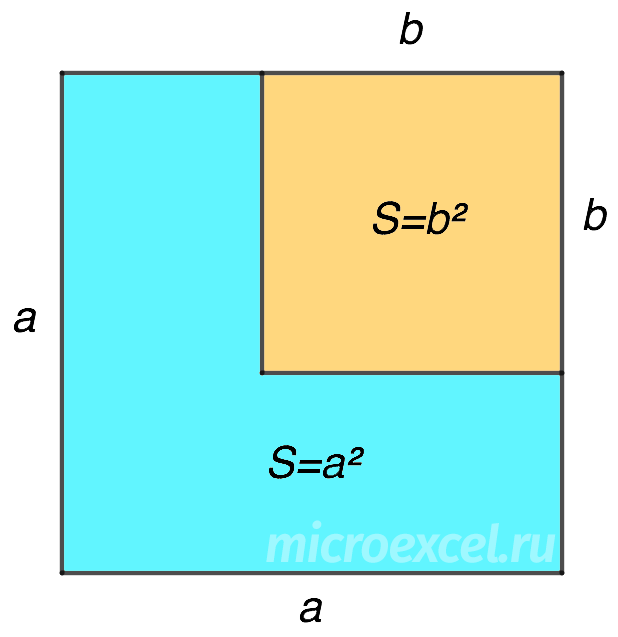
Задача состоит в том, чтобы найти площадь фигуры голубого цвета ( a 2 – b 2 ).

Продолжив любую из линий сторон меньшего квадрата до границ большего мы получим:

• квадрат площадью b 2 ; прямоугольник со сторонами a и ( a-b ); прямоугольник со сторонами b и ( a-b ).

Нам нужна только сумма площадей прямоугольников, которая вычисляется таким образом:

S = a ⋅ (a – b) + b ⋅ (a – b) = a 2 – ab + ba – b 2 = a 2 – b 2

Примеры задач

упражнение 1
Раскройте скобки: (8х — 3у)(8х + 3у).

Решение
Воспользуемся формулой сокращенного умножения:
(8x — 3y)(8x + 3y) = 64×2 — 9y2

Задача 2
Фактор выражения: 25×2 — y2.

Решение
Используем формулу в обратном порядке:
25×2 — y2 = (5x — y)(5x + y)

Обследование
(5x — у)(5x + у) = 25×2 + 5xy — 5xy — y2 = 25×2 — y2

Фактор выражения:

.

Решение: это выражение можно разложить по формуле «разность квадратов»:

.

Пример 2

Решите неравенство

Решение:

В левой части неравенства можно использовать формулу разности квадратов (мысленно заменить выражение
переменная , А
переменная ):

Отвечать:

Упрощать:

Решение: .

Отвечать:

Умножить .

Решение: .

Отвечать:

Пример 5

Решите уравнение: .

Решение:

или

или 

и

Поскольку исходное уравнение имеет шестую степень, ответ будет иметь шесть корней.

Отвечать:
и

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

• ax 2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
• ax 2 + c = 0, при b = 0;
• ax 2 + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax 2 = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0.

Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0.

Пример 1. Решить −6x 2 = 0.

1. Замечаем, что данному уравнению равносильно x 2 = 0, значит исходное уравнение имеет единственный корень — нуль.
2. По шагам решение выглядит так:

Как решить уравнение ax 2 + с = 0

Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:

• перенесем c в правую часть: ax 2 = — c,
• разделим обе части на a: x 2 = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней.

В двух словах

Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению х 2 = -c/a, которое:

не имеет корней при — c/а 0.

Пример 1. Найти решение уравнения 8x 2 + 5 = 0.

1. Перенесем свободный член в правую часть:

Разделим обе части на 8:

В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8x 2 + 5 = 0 не имеет корней.

Как решить уравнение ax 2 + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:

Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня:

Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0

Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.
Решить линейное уравнение:

0,5x = 0,125, х = 0,125/0,5

Значит корни исходного уравнения — 0 и 0,25.

Ответ: х = 0 и х = 0,25.

Как разложить квадратное уравнение

С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:

Формула разложения квадратного трехчлена

Если x₁ и x₂ — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x₁) (x − x₂).

Фсу – формулы сокращённого умножения по алгебре за 7 класс с примерами

Основная задача формул сокращённого умножения

Формулы сокращённого умножения (ФСУ) нужны для того, чтобы умножать и возводить в степень числа, выражения, в том числе многочлены. То есть, при помощи формул можно работать с числами значительно быстрее и проще. Таким образом можно из сложного уравнения сделать обычное, что упростит задачу.

Таблица с формулами сокращённого умножения

Квадрат суммы		Квадрат первого выражения плюс удвоенного произведение первого и второго выражения, плюс квадрат второго выражения.
Квадрат разности		Квадрат разности двух выражений равен квадрату первого выражения, минус удвоенное произведение первого выражения на второе, плюс квадрат второго выражения.
Куб суммы		Куб разности двух выражений равен кубу первого выражения плюс утроенное произведение первого выражения в квадрате на второе выражение, плюс утроенное произведение первого выражения на второе в квадрате, плюс второе выражение в кубе.
Куб разности		Куб разности двух величин равен первое выражение в кубе минус утроенное произведение первого выражения в квадрате на второе выражение, плюс утроенное произведение первого выражения на второе в квадрате, минус второе выражение в кубе.
Разность квадратов		Разность квадратов первого и второго выражений равен произведению разности двух выражений и их суммы.
Сумма кубов		Произведение суммы двух величин на неполный квадрат разности равно сумме их кубов.
Разность кубов		Произведение разности двух выражений на неполный квадрат суммы равно разности их кубов.

Формулы сокращенного умножения (скачать таблицу для печати)

Обратите внимание на первые четыре формулы. Благодаря им можно возводить в квадрат или куб суммы (разности) двух выражений

Что касается пятой формулы, её нужно применять, чтобы вкратце умножить разность или сумму двух выражений.

Две последние формулы (6 и 7) применяются, чтобы умножать суммы обоих выражений на их неполный квадрат разности или суммы.

Вышеперечисленные формулы довольно-таки часто нужны на практике. Именно поэтому их желательно знать наизусть.

Если вам попался пример, разложить многочлен на множители, тогда во многих случаях нужно левую и правую часть переставить местами.

Такую же процедуру можно проделывать и с остальными формулами.

Доказательство ФСУ

Шаг первый.

Возведём a + b во вторую степень. Для этого степень трогать не будем, а выполним банальное умножение:  = x .

Шаг второй. Теперь и выносим за скобки: x + x .

Шаг третий. Раскрываем скобки: x + x + x + x .

Шаг четвёртый. Умножаем, не забывая о знаках: x + x + .

Шаг пятый. Упрощаем выражение: .

Точно так же можно доказать абсолютно любую формулу сокращённого умножения.

Примеры и решения с помощью ФСУ

Как правило, эти семь формул применяются тогда, когда нужно упростить выражение, чтобы решить какое-либо уравнение и даже обычный пример.

Пример 1

• Задание
• Упростите выражение:
• Как видно, к этому примеру подходит первая формула сокращённого умножения – Квадрат суммы.
• Решение

Исходя из первой формулы надо пример разложить на множители. Для этого смотрим на формулу и вместо букв подставляем цифры. В нашем случае «а» – это 3x, а «b» – это 5:

1. x x +
2. Считаем правую часть и записываем результат. У нас получается:
3. + x x +
4. В примере надо умножить всё то, что умножается и сразу получаем ответ:

Конечно же, есть примеры и с дробями. Но, если научитесь решать простые примеры, тогда другие виды вам будут не страшны.

Пример 2

• Задание
• Упростите выражение
• Решение
• = – x x + =

Пример 3

1. Задание
2. Представьте в виде квадрата двучлена трёхчлен
3. Решение
4. Здесь квадраты выражений – и
5. Выражения, которые возводились в квадрат – и
6. Удвоенное произведение этих выражений – , который совпадает с со вторым членом трёхчлена (со знаком «плюс), значит,

Итак, как видно, ничего сложно в примерах нет. Главное, знать формулы, где их можно применять, а где можно обойтись и без них.

Полезные источники

1. Арефьева И. Г., Пирютко О. Н. Алгебра: учебник пособие для 7 класса учреждений общего среднего образования: Минск “Народная Асвета”, 2017 – 304 с.
2. Никольский С. М., Потапов М. К. Алгебра 7 класс: М: 2015 – 287 с.
3. Рубин А. Г., Чулков П. В. Алгебра. 7 класс. М: 2015 – 224 с.

Формула разности квадратов

Формулу разности квадратов относят к формулам сокращенного умножения. Формулы сокращенного умножения используют для упрощения алгебраических выражений или разложения их на множители.

Формулу используют для упрощения выражений посредством раскрытия скобок и разложения многочлена на множители.

Любая формула сокращенного умножения формирует тождество = используем формулы как справа налево, так и слева направо.

Примечание 2

Формула: \(a^2-b^2=(a-b)(a+b)\).

Вместо букв a и b могут использовать любые другие буквы или целые выражения.

Читается: «Разность квадратов a и b равна произведению разности a и b на сумму a и b». Или  «Разность квадратов двух выражений = произведению суммы выражений на их разность».

Тождество верно в обоих направлениях, то есть, разность выражений, умноженная на сумму этих же выражений, равны разности квадратов этих выражений.

Формула: \((a-b)(a+b)=a^2-b^2\).

ФСУ: таблица, примеры использования

Определение

Формулы сокращенного умножения (ФСУ) используются для возведения в степень и умножения чисел, выражений. ФСУ помогают производить вычисления быстрее и делают их более компактными.

В нашей статье будут перечислены все необходимые формулы сокращенного умножения, а также, для удобства запоминания, формулы структурируем в таблицу, разберём примеры применения ФСУ, рассмотрим, как сократить формулы сокращенного умножения, наибольшее внимание уделим способам доказательства ФСУ

Формулы сокращенного умножения (ФСУ): таблица

Тема «Формулы сокращенного умножения» занимает центральное место в школьном курсе алгебры. Математика без формулы сокращенного умножения была бы скучна и сложна. Школьники начинают знакомство с этими формулами в 7 классе курса алгебры. Ниже приведены основные ФСУ формулы сокращенного умножения.

Чтобы с лёгкостью использовать формулы, их нужно заучить наизусть. Сгруппируем их в таблицу и представим ниже, заключив в рамку.

Треугольник Паскаля – это арифметический треугольник. Он назван в честь Блеза Паскаля. Он состоит из коэффициентов одночленов, входящих в состав формулы степени суммы двух чисел. Если схематично очертить этот треугольник Паскаля, то получим равнобедренный треугольник, у которого по бокам стоят единицы. Каждое нижнее число получается путем сложения двух чисел, стоящих выше него.

Можно заметить, что формулы сокращенного умножения квадрат(куб) суммы (разности) – это частный случай формулы бинома Ньютона, когда n=2 и n=3.

Если слагаемых больше, чем два, как выполнить возведение в степень? Полезно вывести формулу квадрата суммы слагаемых, больших, чем два.

Помимо, запоминания формулы, её нужно научиться правильно читать. Данная выше формула, читается так: «Квадрат суммы n слагаемых равен сумме квадратов всех слагаемых и удвоенных произведений всех возможных пар этих слагаемых».

Еще одной нужной формулой в вычислениях является формула разности n-ых степеней 2-х слагаемых.

Практическое применение формул сокращенно умножения, особенности преподавания в школе

В современной системе образования преобладает системно-деятельностный подход. Это означает, что инициатива к поглощению знаний должна исходить от ученика, а учителю следует только направлять его в нужном направлении. У многих учащихся отсутствует интерес к учёбе, они ссылаются на то, что эти знания нигде не пригодятся в жизни. Как быть учителю в данной ситуации? Какие способы мотивации изучения формул сокращенного умножения найти? Эти замечательные формулы еще как пригодятся в житейских ситуациях. В частности, при подборе строительного материала для дома. Например, вы пришли в супермаркет, и продавец по размеру пола (106 м) навязывает 13 000 м2 паркетной доски. Зная ФСУ, вы с лёгкостью в уме сможете проверить, не обманывает ли вас работник магазина.

(106 м)2=(100+6) 2=10 000+2*100*6+36= 11236 м2

Оказывается, вам достаточно будет 11236 м2.

И так можно вывести абсолютно любую формулу. Главное, уметь упрощать выражения, умножать, приводить подобные слагаемые. Кроме аналитического доказательства формул сокращенного умножения, имеет место быть еще и геометрический. О нём нельзя не упомянуть на уроках алгебры. Полезно будет дать это задание в качестве домашнего в рамках исследовательской деятельности учащихся.

Алгебра. 7 класс

Конспект урока

Перечень вопросов, рассматриваемых в теме:

• Формулы сокращённого умножения.
• Куб суммы. Куб разности.
• Разложение многочлена на множители.
• Тождественные преобразования.
• Вычисление значения числовых выражений.

Формулы сокращённого умножения.

a 3 + b 3 = (a + b)(a 2 – ab + b 2 )

a 3 – b 3 = (a – b)(a 2 + ab + b 2 )

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

(a – b) 3 = a 3 – 3a 2 b + 3ab 2 – b 3

• упрощение умножения многочленов;
• разложение многочлена на множители;
• вычисление значения числового выражения;
• тождественные преобразования.

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

(a + b) 3 = (a + b) 2 (a + b) = (a 2 + 2ab + b 2 )(a + b).

Применив правило умножения многочленов, и приведя подобные члены, получим:

a 3 + 2a 2 b + b 2 a + a 2 b + 2ab 2 + b 3 = a 3 + 3a 2 b + 3ab 2 + b 3 .

Итак, доказано равенство, которое называют «куб суммы»: (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

Читается так: «куб суммы двух чисел равен кубу первого числа, плюс утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа и квадрата второго, плюс куб второго числа».

Аналогично докажем формулу «куб разности».

(a – b) 3 = (a – b) 2 (a – b) =(a 2 – 2ab + b 2 )(a – b)

Применив правило умножения многочленов, получим:

a 3 – 2a 2 b + b 2 a – a 2 b + 2ab 2 – b 3 = a 3 – 3a 2 b + 3ab 2 – b 3

Доказано равенство, которое называют «куб разности»:

(a – b) 3 = a 3 – 3a 2 b + 3ab 2 – b 3

Читается так: «куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа и квадрата второго, минус куб второго числа».

Формулы суммы и разности кубов часто используют для упрощения выражений.

Разбор решения заданий тренировочного модуля.

(a + 3) 3 = a 3 + 3a 2 · 3 + 3a · 3 2 + 3 3 = a 3 + 9a 2 + 27a + 27.

(10 – a) 3 =10 3 – 3 · 10 2 a + 3 · 10 · a 2 – a 3 = 1000 – 300a + 30a 2 – a 3 .

Упростите: x 3 + 3x(x + 4) – (x + 2) 3

x 3 + 3x 2 + 12x – (x 3 + 6x 2 + 12x + =

Примеры и решения с помощью ФСУ

Как правило, эти семь формул применяются тогда, когда нужно упростить выражение, чтобы решить какое-либо уравнение и даже обычный пример.

Пример 1

Задание

Упростите выражение:

Как видно, к этому примеру подходит первая формула сокращённого умножения – Квадрат суммы.

Решение

Исходя из первой формулы надо пример разложить на множители. Для этого смотрим на формулу и вместо букв подставляем цифры. В нашем случае «а» – это 3x, а «b» – это 5:

x x +

Считаем правую часть и записываем результат. У нас получается:

+ x x +

В примере надо умножить всё то, что умножается и сразу получаем ответ:

Конечно же, есть примеры и с дробями. Но, если научитесь решать простые примеры, тогда другие виды вам будут не страшны.

Пример 2

Задание

Упростите выражение

Решение

= – x x + =

Пример 3

Задание

Представьте в виде квадрата двучлена трёхчлен

Решение

Здесь квадраты выражений – и

Выражения, которые возводились в квадрат – и

Удвоенное произведение этих выражений – , который совпадает с со вторым членом трёхчлена (со знаком «плюс), значит,

Итак, как видно, ничего сложно в примерах нет. Главное, знать формулы, где их можно применять, а где можно обойтись и без них.

Полезные источники

1. Арефьева И. Г., Пирютко О. Н. Алгебра: учебник пособие для 7 класса учреждений общего среднего образования: Минск “Народная Асвета”, 2017 – 304 с.
2. Никольский С. М., Потапов М. К. Алгебра 7 класс: М: 2015 – 287 с.
3. Рубин А. Г., Чулков П. В. Алгебра. 7 класс. М: 2015 – 224 с.

Разность квадратов

Пусть есть два числа, одно из которых равно a, а другое – b. Их сумма будет равна a + b, а разность составляет a– b. Оба эти выражения являются многочленами.

Теперь перемножим сумму и разность, пользуясь правилами перемножения многочленов (см. урок 6) :

(a + b)(a — b) = a2 — ab + ba — b2

Слагаемые – a b и b a являются подобными, их сумма равна нулю:

-ab + ab = -1ab + 1ab = ab(-1 + 1) = ab * 0 = 0

Поэтому в выражении их можно сократить:

(a + b)(a — b) = a2 — ab + ba — b2 = a2 — b2

Получается, что произведение суммы двух чисел на их разность равно разности их квадратов. Естественно, как и любое другое математическое равенство, это можно переписать в обратном порядке:

a2 — b2  = (a + b)(a — b)

Данное тождество называют формулой разности квадратов.

Вместо a и b в это тождество можно подставлять любые числа, выражения, одночлены, многочлены. Убедимся в ее справедливости на нескольких примерах. Вычислим значение выражения

72 — 52

сначала напрямую, а потом с помощью формулы разности квадратов:

72 — 52 = 7*7 — 5*5 = 49 — 25 = 24

72 — 52 = (7 — 5)(7 + 5) = 2*12 = 24

Видно, что ответ не зависит от способа вычисления. Однако в ряде один из них представляется более удобным.

Пример. Вычислите разность двух квадратов: 25162 и 15162.

Решение. Возводить во вторую степень четырехзначные числа без калькулятора тяжело, поэтому используем сокращенное умножение:

25162 — 15162 = (2516 + 1516)(2516 + 1516) = 4032 * 1000 = 4032000

Ответ: 4032000

Пример. Вычислите 499•501.

Решение. Используем две простые замены:

499 = 500 — 1

501 = 500 + 1

С их помощью вычисления существенно упрощаются, так как произведение можно представить как разность квадратов двух чисел:

499 * 501 = (500 — 1)(500 + 1) = 5002 — 12 = 250000 — 1 = 249999

Ответ: 249999.

Пример. Докажите, что число 7658732 – 7658642 делится на 9.

Решение. Разность квадратов равна:

7658732 – 7658642 = (765873 — 765864)(765873 + 765864) = 9*(765873 + 765864)

Даже не складывая слагаемые во второй скобке, мы можем сказать, что исходное число делится на 9, так как на 9 делится один из множителей, на которые мы разложили разность квадратов.

Теперь рассмотрим случаи, когда в формулу подставляются переменные. Пусть необходимо найти произведение полиномов 8u + 5v и 8u– 5v. С помощью формулы сокращенного умножения получаем:

(8u + 5v)(8u — 5v) = (8u)2 — (5v)2 = 64u2 — 25v2

Конечно, мы могли бы выполнить эту операцию и без использования сокращенного умножения, просто раскрыв скобки методом «фонтанчика». Но тогда мы потратили бы больше времени, усилий и бумаги:

(8u + 5v)(8u — 5v) = (8u)2 — 8u*5v + 5v*8u — (5v)2 = 64u2 — 25v2

Пример. Перемножьте полиномы x2z +2y3 и x2z– 2y3.

Решение.

(x2z +2y3)(x2z +2y3) = (x2z)2 — (2y3)2 = x4z2 — 4y6

Пример. Упростите выражение

-3.5m2 — (1.5n — 2m)(1.5n + 2m)

Решение:

-3.5m2 — (1.5n — 2m)(1.5n + 2m) = -3.5m2 — ((1.5n)2 — (2m)2) = -3.5m2 — 2.25n2 + 4m2 = 0.5m2 — 2.25n2

Иногда с помощью сокращенного умножения можно разложить полином на множители. Например, двучлен x2– 25 можно представить как

x2 — 25 = x2 — 52 = (x — 5)(x + 5)

С помощью разложения разности квадратов на множители можно доказать, что разность вторых степеней двух последовательных натуральных чисел всегда является нечетным числом. Обозначим за n произвольное натуральное число. Тогда следующим за ним будет число n+1. Разность их квадратов равна

(n + 1)2 = n2

Раскроем скобки:

(n + 1)2 — n2 = (n + 1 — n)(n + 1 + n) = 1*(2n + 1) = 2n + 1 = 1*(2n + 1) = 2n + 1

Число 2n +1 при делении на 2 дает остаток 1, то есть является нечетным.

Стоит отметить, что для суммы квадратов a2 + b2 аналогичной формулы разложения на множители не существует.

Пример задачи с решением

Задача №7

Сократить дробь:

Решение.

В числителе записан квадрат разности, а в знаменателе – разность квадратов двух выражений. Применяя соответствующие формулы, получается искомый результат:

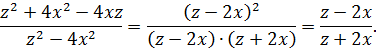
Ответ:

В большинстве случаев разницы, как сворачивать квадрат двучлена, не существует. Однако в данной ситуации, благодаря выражению в знаменателе, на первое место лучше поставить

Онлайн калькуляторы помогают выполнять преобразования. Однако, поскольку формулы сокращённого умножения являются базовым материалом школьного курса, то лучше не просто получить результат, но и понять, каким образом к нему пришли.

Формулы сокращенного умножения.

Формулы сокращенного умножения.

Формулы сокращенного умножения. Разность квадратов, сумма кубов и разность кубов и разность четвертых степеней. Квадрат суммы и квадрат разности и куб суммы и куб разности.

Разность квадратов	a2-b2 = (a-b)(a+b)
Квадрат суммы	(a+b)2 = a2+2ab+b2
Квадрат разности	(a-b)2 = a2-2ab+b2
Куб суммы	(a+b)3 = a3+3a2b+3ab2+b3
Куб разности	(a-b)3 = a3-3a2b+3ab2-b3
Сумма кубов	a3+b3 = (a+b)(a2-ab+b2)
Разность кубов	a3-b3 = (a-b)(a2+ab+b2)
Разность четвертых степеней	a4-b4 = (a2-b2)(a2+b2)=(a-b)(a+b)(a2+b 2)

Справочно, только для тех кто хочет больше представлять тему: Бином Ньютона. Целая положительная степень n суммы. (a + b)n=

3.3. Разложение на множители. Формулы сокращённого умножения

Существует несколько методов, с помощью которых можно представить выражение в виде произведения.

Вынесение за скобки

Этот метод используется, если в каждом слагаемом выражения есть повторяющиеся элементы. Разложим на множители выражение :

1. Определяем одночлен (выражение, представляющее собой произведение отдельных элементов), который есть в каждом слагаемом выражения. В данном случае это .

2. Выносим повторяющиеся элементы за скобку. Для этого каждое слагаемое выражения необходимо разделить на выносимый одночлен и записать частное от деления.

Деление выполняется по обычным правилам, то есть при вынесении одночлена со знаком «–» знак частного меняется на противоположный:

После раскрытия скобок должно получиться исходное выражение. Это свойство можно использовать для проверки.

Группировка

Далеко не всегда в выражении будут повторяющиеся элементы. Но можно попробовать «создать» их самостоятельно. Рассмотрим алгоритм метода, который позволяет это сделать, на примере выражения

1. Сгруппируем отдельные слагаемые таким образом, чтобы в каждой группе появились повторяющиеся элементы. Слагаемые не обязательно должны идти по порядку.

2. В каждой группе вынесем повторяющийся одночлен за скобки.

3. Теперь можно вынести одинаковые выражения точно так же, как выносятся одночлены.

Аналогично можно создавать группы из трех и более слагаемых. Разложим на множители следующее выражение:

1. Группируем отдельные слагаемые.

2. Выносим повторяющиеся элементы за скобку. В некоторых случаях вынести можно только 1.

3.Выносим повторяющиеся скобки.

Иногда удобно делить слагаемые на три группы (и более). Алгоритм решения при этом не меняется.

Разложение на множители квадратного трехчлена

Выражения вида , где – некоторые числа, можно представить в виде произведения:

В котором – корни уравнения.

Рассмотрим следующий пример, в котором нужно разложить на множители выражение

1. Определим корни уравнения с помощью дискриминанта или по теореме Виета.

2. Подставим найденные корни в формулу . В данном случае .

Разложение на множители с помощью формул сокращенного умножения

Формулы сокращенного умножения (ФСУ) – готовые формулы по которым можно представить некоторые выражения в виде произведения и наоборот – некоторые произведения в виде выражения, не раскрывая скобки и не приводя подобные слагаемые.

Замечательным свойством этих правил является то, что если вместо стоят другие буквы или выражения, сами формулы остаются неизменными.

Алгоритм разложения на множители с помощью ФСУ

1. Определяем наиболее похожую на выражение формулу.

2. С помощью свойств степеней преобразуем отдельные слагаемые так, чтобы выражение приняло вид, определенный в пункте 1.

3. Используем соответствующую формулу.

Рассмотрим несколько задач, в которых применяется данный алгоритм.

Пример 1

1. Выражение похоже на квадрат суммы.

2. Преобразуем отдельные слагаемые:

3. Воспользуемся формулой квадрата суммы:

Пример 2

1. Выражение похоже на разность кубов.

2. Преобразуем отдельные слагаемые:

3. Воспользуемся формулой разности кубов:

Пример 3

1. Выражение похоже на разность квадратов.

2. Преобразуем отдельные слагаемые:

3. Воспользуемся формулой разности квадратов:

Упрощение дробей

Дробно-рациональное выражение можно упростить, если представить в виде произведения числитель и знаменатель (с помощью любого правила, приведенного выше), а затем сократить повторяющиеся множители.

Упростим выражение :

1. В числителе вынесем повторяющийся элемент за скобки, а знаменатель свернем по формуле квадрата разности.

2. Сократим повторяющиеся элементы.

Прочитано
Отметь, если полностью прочитал текст