Что такое алгебре ческая сумма

Помогите решить / разобраться (М)

1) Во-первых, почему в приведенных ниже записях как тождественные в качестве индексов переменных используются как переменная индекса, так и ее верхняя граница:(1) и (2)Насколько это правильно?

2) Во-вторых, почему запись(3)означает сумму элементов множества ?

Насколько я понимаю, согласно Википедии выражение после буквы сигма обозначает каждый член в серии суммирования. Например, выражение (2) означает сумму всех членов заданного ряда, у каждого из которых отличаются значения переменной индекса .Но ведь в записи (3) — это тоже переменная, означающая определенную функцию, зависящую от переменной . Тогда логично предположить, что выражение (3) означает сумму всех членов заданного ряда числовых выражений, у каждого из которых отличаются значения переменной , т.е., что.Однако, согласно Википедии:.Но ведь сумму элементов множества можно записать и следующим образом:,что, с моей точки зрения, было бы логичнее.

Очень прошу прояснить данные вопросы, т.к. по всей видимости мое личное мнение ошибочно. Возможно есть какая-нибудь литература, в которой не слишком сложно изложены правила использования алгебраической суммы?

Примеры задач с решением

Рассмотрим как решать задачи на заданную тему.

Пример 1

Требуется вычислить 574 член в ряду арифметической прогрессии, первые три члена которой «8, 15, 22…».

Вариант рассуждений по примеру 1. Для нахождения любого конкретного элемента ряда нам необходима информация о значении первого члена (a1) и о разности (d). Чтобы вычислить разность, вычитаем из второго члена ряда первый (15 – и получаем d = 7. Теперь мы можем считать по формуле:

Подставляя полученные значения, получим выражение вида a574 = 8 + (574-1) * 7.

После вычисления получаем ответ: a574 = 4019.

Пример 2

Требуется вычислить 544 член ряда, являющийся арифметической прогрессией, при условии, что 154-ый член равен 17, а разность (d) равна 8.

Вариант рассуждений по примеру 2. Пользоваться в данной ситуации мы будем формулой из предыдущего примера:

Подставляя известные значения, получаем выражение – а544 = 17 + (544 1) * 8.

Вычисляя, получаем ответ а544 = 4361.

Пример 3

Для подготовки к экзамену по биологии студенту Смирнову необходимо выучить 730 вопросов (включая загадки). Известно, что он весьма обеспокоен и по мере приближения даты экзамена учит ежедневно на 27 вопросов больше, чем в предыдущий день. Друг Смирнова выяснил, что тот в первый день выучил всего 17 вопросов.

Требуется выяснить, сколько времени у студента ушло на подготовку.

Вариант рассуждений по примеру 3. Очевидно, что случай с подготовкой студента к экзамену решается через формулы арифметической прогрессией (поскольку присутствует фиксированная разность d = 17). Производим подстановку известных данных:

После подстановки получаем выражение: 730 = 17 + (n 1) * 27.

После вычислений определяем ответ – 27 дней.

Арифметическая прогрессия является наиболее простой из всех числовых зависимостей. Использование описанных формул позволит намного ускорить вычисления в задачах, где это требуется.

Кроме этого, для упрощения можно использовать онлайн калькулятор. В школе данную тему изучают в программе за 9 класс, а основные задания касаются нахождения членов и сумм.

Девушки бывают разные, но найти среди них идеальную непросто. Зато вы легко найдете свой идеал в сексе на пару часов или горячую ночку, если полюбопытствуете в нашем каталоге проститутки Самара Барышни легки на подъем, легки в общении, характером обладают тоже легким, а еще легче – их поведение!

Рациональные выражения

В школе до изучения иррациональных чисел работа ведется исключительно с рациональными выражениями. Дадим определение рационального выражения.

Определение.

Числовые и буквенные выражения, в которых используются рациональные числа и буквы, а также операции сложения, вычитания, умножения, деления (деление может быть обозначено дробной чертой) и возведения в целую степень, называются рациональными выражениями.

Важное пояснение: в рациональных выражениях не могут присутствовать знаки и функции, которые могут внести иррациональность. Иными словами, в рациональных выражениях не должно быть знаков радикала (корней), степеней с дробными и иррациональными показателями, степеней с переменными в показателе, логарифмов, тригонометрических функций и т.п.. Теперь можно привести примеры рациональных выражений

Отталкиваясь от данного выше определения, можно утверждать, что числовые выражения и являются рациональными выражениями. Рациональным является и буквенное выражение , а также выражения с переменными вида a·x2+b·x+c и .

Теперь можно привести примеры рациональных выражений. Отталкиваясь от данного выше определения, можно утверждать, что числовые выражения и являются рациональными выражениями. Рациональным является и буквенное выражение , а также выражения с переменными вида a·x2+b·x+c и .

Рациональные выражения подразделяются на целые рациональные выражения и дробные рациональные выражения.

Целые рациональные выражения

Определение.

Целыми рациональными выражениями называются рациональные выражения, которые не содержат деления на выражения с переменными и выражений с переменными в отрицательной степени.

Согласно данному определению, целыми рациональными выражениями являются, например, буквенное выражение a+1, выражение с тремя переменными вида x2·y3−z+3/2 и дробь .

А выражения x:(y−1) и не являются целыми рациональными, так как содержат деление на выражение с переменными.

Дробные рациональные выражения

Определение.

Если рациональное выражение содержит деление на выражение с переменными и/или выражение с переменными в отрицательной степени, то оно называется дробным рациональным выражением.

Данное определение позволяет привести примеры дробных рациональных выражений. К примеру, выражения 1:x, и являются дробными рациональными.

А вот рациональные выражения (2·x−x2):4 и не содержат деления на выражения с переменными и отрицательных степеней выражений с переменными, поэтому они не являются дробными рациональными выражениями.

Применение преобразований

Алгебраические выражения, показывающие, что одна величина больше другой или равна ей, называют уравнениями и равенствами. При этом их используют для составления формул, то есть для записи, выражающей зависимость между двумя или несколькими переменными. Это удобно, так как преобразования позволяют привести формулу к простому для запоминания виду.

При решении примеров важно знать все существующие методы. Какой из них применять, конкретно указать нельзя, всё зависит от личных предпочтений и опыта решения подобных заданий

Например, пусть нужно упростить сложное выражение (a3 (b — c) + b3 (c — a) + c3 (a — b)) / (a2 (b — c) + b2 (c — a) + c2 (a — b)).

Сначала можно попробовать разложить на множители делитель и делимое. Один из вариантов преобразования числителя следующий:

a3 (b — c) + b3 (c — a) + c3 (a — b) = a3b — b3c — a3c + b3c + c3(a — b) = ab (a2 — b2) = ab (a2 — b2) — c (a3 — b3) + c3(a — b) = (a — b) (ab (a + b) — c (a2 + ab + b2) + c3 = (a — b) (a2b — a2c + ab2 — abc + c3 — cb2) = (a — b) (a2 (b — c) + ab (b — c) — c (b2 — c2) = (a — b) (b — c) (a2 — c2 + ab — cb) = (a — b) (b — c) (a — c) (a + b + c).

По аналогии раскладывая знаменатель, можно прийти к результату: (a — b) (b — c) (a — c). В итоге получится равенство (a3 (b — c) + b3 (c — a) + c3 (a — b)) / (a2 (b — c) + b2 (c — a) + c2 (a — b)) = ((a — b) (b — c) (a — c) (a + b + c)) / ((a — b)(b — c)(a — c)) = a + b + c.

В числителе возможно выделить множитель (a — b) на том основании, что делимое равно нулю, когда a совпадает с b. Обычно в двух взаимно обратных операциях выполнение одной сложнее, чем другой. Это касается, в частности, выполнения умножения алгебраических выражений и разложения на множители или возведения в степень с извлечением корня. Например, легко увидеть, что (5 + 3 √2)2 = 43 + 30 √2, но значительно труднее прочитать это равенство справа налево.

Следует помнить, что когда при решении задачи встречается выражение подкоренного вида √с + n * √k или √a + b√k, то необходимо попытаться добыть соответствующий корень. Если же это невозможно, то нужно воспользоваться подбором.

Примеры решения уравнений

Сегодня мы занимаемся линейными уравнениями, причем только простейшими. Вообще, под линейным уравнением подразумевается всякое равенство, содержащее в себе ровно одну переменную, и она идет лишь в первой степени.

Решаются такие конструкции примерно одинаково:

1. Прежде всего необходимо раскрыть скобки, если они есть (как в нашем последнем примере);
2. Затем свести подобные
3. Наконец, уединить переменную, т.е. всё, что связано с переменной — слагаемые, в которых она содержится — перенести в одну сторону, а всё, что останется без неё, перенести в другую сторону.

Затем, как правило, нужно привести подобные с каждой стороны полученного равенства, а после этого останется лишь разделить на коэффициент при «иксе», и мы получим окончательный ответ.

В теории это выглядит красиво и просто, однако на практике даже опытные ученики старших классов могут допускать обидные ошибки в достаточно простых линейных уравнениях. Обычно ошибки допускаются либо при раскрытии скобок, либо при подсчёте «плюсов» и «минусов».

Кроме того, бывает так, что линейное уравнение вообще не имеет решений, или так, что решением является вся числовая прямая, т.е. любое число. Эти тонкости мы и разберем в сегодняшнем уроке. Но начнем мы, как вы уже поняли, с самых простых задач.

Расчеты электрических цепей с помощью законов Кирхгофа.

Теперь давайте рассмотрим вариант сложной цепи, и я вам расскажу, как на практике применять законы Кирхгофа.

Итак, на рисунке 4 имеется сложная цепь с двумя источниками ЭДС величиной E₁=12 в и E₂=5 в , с внутренним сопротивлением источников r₁=r₂=0,1 Ом, работающих на общую нагрузку R = 2 Ома. Как же будут распределены токи в этой цепи, и какие они имеют значения, нам предстоит выяснить.

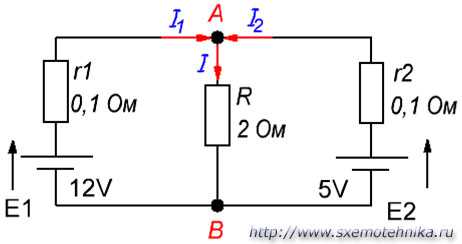
Рисунок 4. Пример расчета сложной электрической цепи.

Теперь согласно первому закону Кирхгофа для узла А составляем такое выражение:

I = I₁ + I₂,

так как I₁ и I₂ втекают в узел А, а ток I вытекает из него.

Используя второй закон Кирхгофа, запишем еще два выражения для внешнего контура и внутреннего левого контура, выбрав направление обхода по часовой стрелке.

Для внешнего контура:

E₁-E₂ = Ur₁ – Ur₂ или E₁-E₂ = I₁*r₁ – I₂*r₂

Для внутреннего левого контура:

E₁ = Ur₁ + UR или E₁ = I₁*r₁ + I*R

Итак, у нас получилась система их трех уравнений с тремя неизвестными:

I = I₁ + I₂;

E₁-E₂ = I₁*r₁ – I₂*r₂;

E₁ = I₁*r₁ + I*R.

Теперь подставим в эту систему известные нам величины напряжений и сопротивлений:

I = I₁ + I₂;

7 = 0,1I₁ – 0,1I₂;

12 = 0,1I₁ +2I.

Далее из первого и второго уравнения выразим ток I₂

I₂=I — I₁;

I₂ = I₁ – 70;

12 = 0,1I₁ + 2I.

Следующим шагом приравняем первое и второе уравнение и получим систему из двух уравнений:

I — I₁= I₁ – 70;

12 = 0,1I₁ + 2I.

Выражаем из первого уравнения значение I

I = 2I₁– 70;

И подставляем его значение во второе уравнение

12 = 0,1I₁ + 2(2I₁ – 70).

Решаем полученное уравнение

12 = 0,1I₁ + 4I₁ – 140.

12 + 140= 4,1I₁

I₁=152/4,1

I₁=37,073 (А)

Теперь в выражение I = 2I₁– 70 подставим значение

I₁=37,073 (А) и получим:

I = 2*37,073 – 70 = 4,146 А

Ну, а согласно первому закона Кирхгофа ток I₂=I — I₁

I₂=4,146 — 37,073 = -32,927

Знак «минус» для тока I₂ означает, то что мы не правильно выбрали направление тока, то есть в нашем случае ток I₂ вытекает из узла А.

Теперь полученные данные можно проверить на практике или смоделировать данную схему например в программе Multisim.

Скриншот моделирования схемы для проверки законов Кирхгофа вы можете посмотреть на рисунке 5.

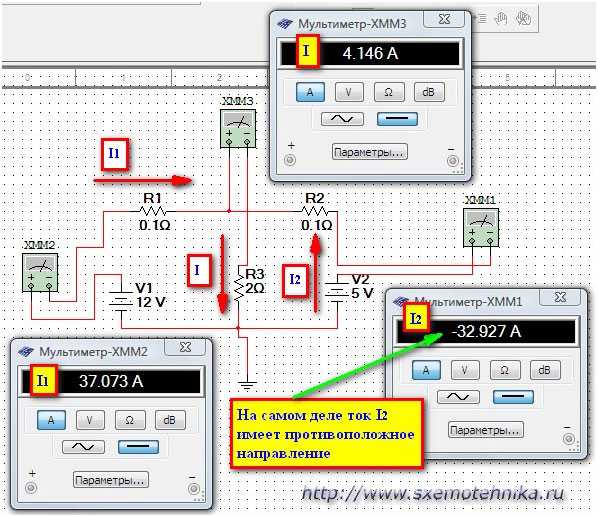 Рисунок 5. Сравнение результатов расчета и моделирования работы цепи.

Для закрепления результатата предлагаю посмотреть подготовленное мной видео:

Сумма числового ряда

Числовой ряд можно рассматривать как систему приближений к числам. Для его обозначения применяют формулу:

Здесь показана начальная последовательность чисел ряда и правило суммирования:

• ∑ — математический знак суммы;
• a_i — общий аргумент;
• _i — переменная, правило для изменения каждого последующего аргумента;
• ∞ — знак бесконечности, «предел», до которого проводится суммирование.

Запись обозначает: суммируются натуральные числа от 1 до «плюс бесконечности». Так как _i = 1, то подсчет суммы начинается с единицы. Если бы здесь стояло другое число (например, 2, 3), то суммировать мы начинали бы с него (с 2, 3).

В соответствии с переменной _i ряд можно записать развернуто:

= а₁ + а₂ + а₃ + а₄ + а₅ + … (до «плюс бесконечности).

Определение суммы числового ряда дается через «частичные суммы». В математике они обозначаются Sn. Распишем наш числовой ряд в виде частичных сумм:

Сумма числового ряда – это предел частичных сумм S_n. Если предел конечен, говорят о «сходящемся» ряде. Бесконечен – о «расходящемся».

Сначала найдем сумму числового ряда:

Теперь построим в Excel таблицу значений членов ряда:

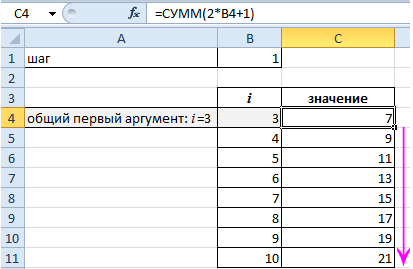
Общий первый аргумент берем из формулы: i=3.

Все следующие значения _i находим по формуле: =B4+$B$1. Ставим курсор в нижний правый угол ячейки В5 и размножаем формулу.

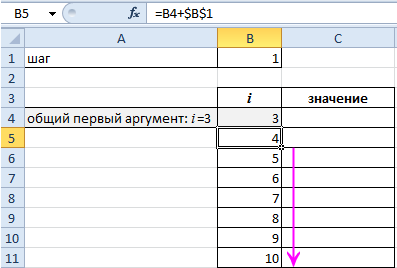
Найдем значения. Делаем активной ячейку С4 и вводим формулу: =СУММ(2*B4+1). Копируем ячейку С4 на заданный диапазон.

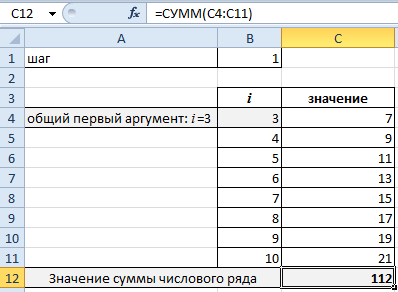
Значение суммы аргументов получаем с помощью функции: =СУММ(C4:C11). Комбинация горячих клавиш ALT+«+» (плюс на клавиатуре).

Решаем реальные примеры простых линейных уравнений

Задача №1

На первом шаге от нас требуется раскрыть скобки. Но их в этом примере нет, поэтому пропускаем данный этап. На втором шаге нам нужно уединить переменные

Обратите внимание: речь идет лишь об отдельных слагаемых. Давайте запишем:

Приводим подобные слагаемые слева и справа, но тут уже это сделано. Поэтому переходим к четвертому шагу: разделить на коэффициент:

\

Вот мы и получили ответ.

Задача №2

В этой задаче мы можем наблюдать скобки, поэтому давайте раскроем их:

И слева и справа мы видим примерно одну и ту же конструкцию, но давайте действовать по алгоритму, т.е. уединяем переменные:

Приведем подобные:

При каких корнях это выполняется. Ответ: при любых. Следовательно, можно записать, что $x$ — любое число.

Задача №3

Третье линейное уравнение уже интересней:

\

Тут есть несколько скобок, однако они ни на что не умножаются, просто перед ними стоят различные знаки. Давайте раскроем их:

Выполняем второй уже известный нам шаг:

\

Посчитаем:

Выполняем последний шаг — делим все на коэффициент при «икс»:

\

Построение графика функций суммы числового ряда

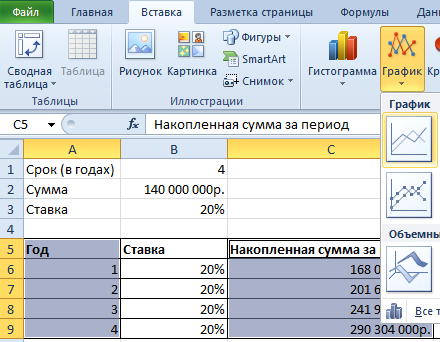
Построим график функций, отражающий рост капитала. Для этого нам нужно построить график функции являющейся суммой построенного ряда. За пример, возьмем те же данные по вкладу:

Дальше нам нужна функция для начисления сложных процентов — БС(). Мы узнаем будущею стоимость инвестиций при условии равных платежей и постоянной процентной ставке. Используя функцию БС(), заполним таблицу:

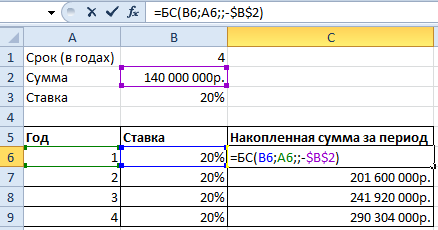
В первой строке показана накопленная сумма через год. Во второй – через два. И так далее.

Сделаем еще один столбец, в котором отразим прибыль:

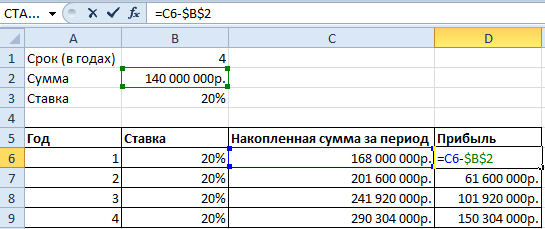
Как мы считали – в строке формул.

На основании полученных данных построим график функций.

Выделим 2 диапазона: A5:A9 и C5:C9. Переходим на вкладку «Вставка» — инструмент «Диаграммы». Выбираем первый график:

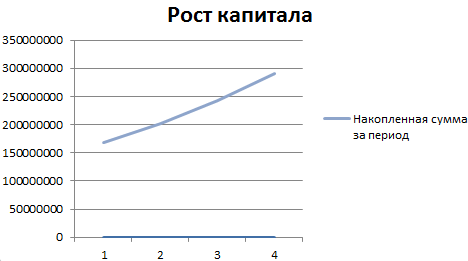
Сделаем задачу еще более «прикладной». В примере мы использовали сложные проценты. Они начисляются на наращенную в предыдущем периоде сумму.

Возьмем для сравнения простые проценты. Формула простых процентов в Excel: =$B$2*(1+A6*B6)

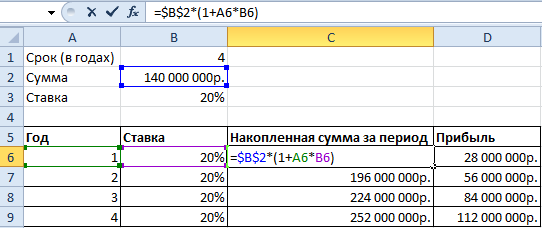
Добавим полученные значения в график «Рост капитала».

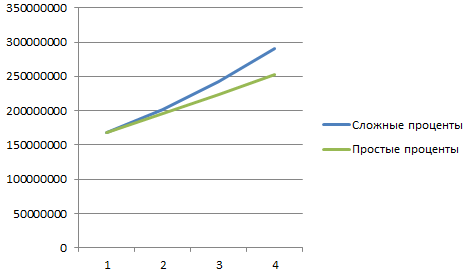
Какие именно выводы сделает инвестор – очевидно.

Математическая формула частичной суммы функционального ряда (с простыми процентами): S_n = a (1 + x*n), где а – первоначальная сумма вклада, х – проценты, n – период.

Примеры решения линейных уравнений

Переходим к практике. Разберем, как применяется алгоритм решения линейных уравнений. Приведем решения характерных примеров, соответствующих различным значениям коэффициентов линейных уравнений.

Пример.

Решите линейное уравнение 0·x−0=0
.

Решение.

В этом линейном уравнении a=0
и b=−0
, что то же самое, b=0
. Следовательно, это уравнение имеет бесконечно много корней, любое число является корнем этого уравнения.

Ответ:

x
– любое число.

Пример.

Имеет ли решения линейное уравнение 0·x+2,7=0
?

Решение.

В данном случае коэффициент a
равен нулю, а коэффициент b
этого линейного уравнения равен 2,7
, то есть, отличен от нуля. Поэтому, линейное уравнение не имеет корней.

В этом видео мы разберём целый комплект линейных уравнений, которые решаются по одному и тому же алгоритму — потому и они и называются простейшими.

Для начала определимся: что такое линейное уравнение и какое их них называть простейшим?

Под простейшим уравнением подразумевается конструкция:

Все остальные линейные уравнения сводятся к простейшим с помощью алгоритма:

1. Раскрыть скобки, если они есть;
2. Перенести слагаемые, содержащие переменную, в одну сторону от знака равенства, а слагаемые без переменной — в другую;
3. Привести подобные слагаемые слева и справа от знака равенства;
4. Разделить полученное уравнение на коэффициент при переменной $x$ .

Разумеется, этот алгоритм помогает не всегда. Дело в том, что иногда после всех этих махинаций коэффициент при переменной $x$ оказывается равен нулю. В этом случае возможны два варианта:

1. Уравнение вообще не имеет решений. Например, когда получается что-нибудь в духе $0\cdot x=8$, т.е. слева стоит ноль, а справа — число, отличное от нуля. В видео ниже мы рассмотрим сразу несколько причин, по которым возможна такая ситуация.
2. Решение — все числа. Единственный случай, когда такое возможно — уравнение свелось к конструкции $0\cdot x=0$. Вполне логично, что какой бы $x$ мы ни подставили, все равно получится «ноль равен нулю», т.е. верное числовое равенство.

А теперь давайте посмотрим, как всё это работает на примере реальных задач.

Применение равенства алгебраической суммы в экономике и физике

Равенство алгебраической суммы является одним из основных принципов в физике и экономике. В физике этот принцип применяется для определения сил, которые действуют на тело. Если на тело действуют несколько сил, то равенство алгебраической суммы этих сил равна нулю. Это означает, что сумма всех сил, направленных вправо, должна быть равна сумме всех сил, направленных влево. Если это равенство не выполняется, то это означает, что на тело действует остаточная сила, которая может двигать тело.

В экономике равенство алгебраической суммы применяется для балансировки финансовой отчетности компаний. Если компания получает определенную сумму дохода, но тратит больше денег, чем зарабатывает, то это приводит к неравенству алгебраической суммы. В таком случае компания должна принять меры по сокращению расходов или увеличению доходов, чтобы снова достичь равенства алгебраической суммы.

Также равенство алгебраической суммы может быть использовано для оценки целесообразности различных финансовых операций, и для того, чтобы найти оптимальный баланс между риском и доходностью. В общем, принцип равенства алгебраической суммы является важным инструментом для оценки и контроля различных физических и экономических процессов.

Как написать знак суммы (количества) в таблицах Excel.

При написании формул в документах MS Excel или Word зачастую возникает потребность в написании математического знака суммы (он же «знак суммирования» или «знак нахождения суммы»). Некоторые далекие от математических исчислений люди называют его «знак количества».

Выглядит знак суммы, как угловатая растянутая относительно горизонтальной оси симметрии заглавная русская буква «Е» или английская «E».

Вставить знак суммы в ячейку таблицы «эксель» или на лист «вордовского» документа можно двумя методами, которые приведены ниже:

При помощи опций на панели быстрого доступа в самой программе.

Как поставить знак суммы при помощи таблицы символов.

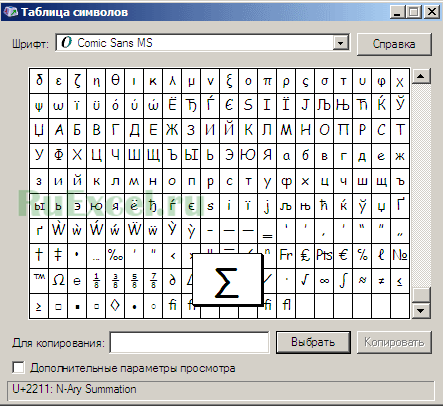
Необходимо последовательно выполнить следующие действия:

• Войти в меню «Пуск» => Программы => Стандартные => Служебные => Таблица символов.
• Выбрать символ суммирования;
• Скопировать символ суммирования;
• Вставить символ в таблицу или документ «Ворда».

Способ нехитрый и не занимает много времени.

Как поставить знак суммы при помощи встроенных возможностей «Эксель».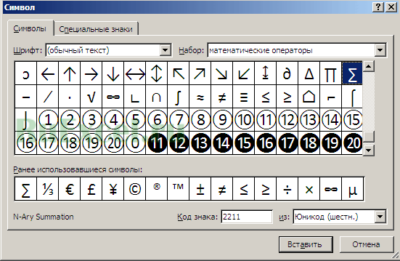

Необходимо выполнить следующую последовательность действий:

• Выбрать ячейку, в которую поставите знак суммы;
• В меню быстрого доступа выбрать вкладку «Вставка»
• Выбрать пиктограмму «Символ»;
• В появившемся окне выбрать знак суммы и вставить его при помощи кнопки «Вставить»

Подробное пошаговое видео о том, как выполняются описанные выше действия:

Иррациональные выражения, выражения с корнями

Знакомство с понятием корня приводит к возникновению выражений, в записях которых присутствуют знаки корней (радикалы). Такие выражения обычно называют выражениями с корнями или выражениями, содержащими операцию извлечения корня. Их же называют иррациональными выражениями.

Определение.

Иррациональные выражения (выражения с корнями) — это выражения, которые содержат в записи знаки корней.

На основании данного определения , a+1/(a1/2+2), и — это все иррациональные выражения, так как в каждом из них присутствует хотя бы один знак корня.

Так как корни тесно связаны со степенями, то они очень часто присутствуют в выражениях совместно. Например, и т.п.

В статье преобразование иррациональных выражений (выражений с корнями) мы поговорим про основные приемы работы с иррациональными выражениями.

Свойства алгебраической суммы

В любой сумме слагаемые можно менять местами и произвольным образом объединять в группы, то есть использовать свойства сложения (переместительное и сочетательное):

10 + (-7) = -7 + 10 = 3

-7 + 28 + (- 13) + 12 = (-7 + (- 13)) + (28 + 12) = -20 + 40 = 20

Описание презентации по отдельным слайдам:

14 . 10. 15 Классная работа

Домашнее задание: решить № 224, 233, 234, 245 (а).

Вывод: каждое из данных выражений является суммой либо положительного и отрицательного, либо двух отрицательных чисел.

Выражения, содержащие числа, знаки + и -, можно представить в виде суммы положительных и отрицательных чисел. Такие выражения называют алгебраическими суммами. . Алгебраическая сумма — это выражение, которое можно представить в виде суммы положительных и отрицательных чисел

Рассмотрим выражения,каждое из которых являются суммой либо положительного и отрицательного,либо двух отрицательных чисел.Такие выражения называются алгебраическими суммами.Рассмотрим применение переместительного и сочетательного законов для чисел любых знаков.Ввести понятие алгебраической суммы,рассмотреть на примерах как можно преобразовывать данные выражения.Например:Назови слагаемые алгебраической суммы,запиши выражение без скобок и найди его значение.Используя законы арифметическиз действий вычисли значение выражения.Составь сумму из данных слагаемых,записать ее со скобками и без скобок.

Лядова Елена АнатольевнаНаписать 5185 13.02.2015

Номер материала: 385619

• 13.02.2015 1550

• 13.02.2015 809

• 13.02.2015 1858

• 13.02.2015 4783

• 13.02.2015 432

• 13.02.2015 721

• 13.02.2015 1151

Не нашли то что искали?

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

обозначающее несколько сложений и вычитаний.

На основании правила вычитания мы можем все вычитания заменить сложением с числами, противоположными вычитаемым. Получим:

Таким образом, все числа в выражении (1) стали слагаемыми.

Определение. Выражение, обозначающее несколько последовательных сложений и вычитаний, называется алгебраической суммой.

В алгебраической сумме всякое вычитание можно заменить прибавлением числа, противоположного вычитаемому.

Заменив в алгебраической сумме все вычитания сложениями, можно записать её в виде суммы, в которой слагаемые могут быть любыми рациональными числами (положительными, отрицательными, равными нулю), а также числами, обозначенными буквами.

Для упрощения записи мы можем везде знак сложения перед скобками опустить, запомнив раз навсегда, что каждый знак в выражении относится к следующему за ним числу и что все эти числа следует сложить.

Так, выражение (2) можно записать короче:

Это выражение и показывает, что надо сложить числа .

В алгебраической сумме всякое сложение можно заменить вычитанием противоположного числа.

Здесь прибавление числа заменено вычитанием числа .

Примеры решения задач

Задача 1.

Теоретическое введение

Функцией переменной величины , называется величина такая, что каждому значению , принадлежащей некоторой области , соответствует единственное значение величины .

Обозначение: .

– область определения функции, – аргумент.

– область изменения функции, – значение;

Функция может быть задана аналитически, таблично, графически.

Основными элементарными функциями являются:

1. 1. степенные (, где – произвольное число)

• показательные (, , )
• логарифмические (,, )
• тригонометрические (, , , )
• обратные тригонометрические (,,, )

Композиция (суперпозиция) двух функций и есть функция, в которой аргументом одной из данных функции, является значение другой функции. Обозначение: и .

Сложная функция есть композиция двух и более функций.

Элементарная функция есть функция, полученная из основных элементарных функций с помощью арифметических действии и композиции.

Целью математического анализа является изучение различных функций, их свойств, и операций связанных с функциями.

Функция называется четной, если для всех своих аргументов.

Функция называется нечетной, если для всех своих аргументов.

Число называется пределом функции при , стремящемся к и обознается , если при неограниченном приближении к , неограниченно приближается .

Свойства пределов:

• Передел суммы двух функций равен сумме пределов этих функций, если они существуют:
• Предел произведения функции равен произведению пределов, если они существуют:
• Предел частного двух функций равен частному пределов, если они существуют, и предел знаменателя не равен нулю: , при .

Обычно , например:

Однако, иногда значение не входит в область определения функции . В этом случае имеются различные методы вычисления пределов:

Выделение общего множителя

Выделение главной части

Использование замечательных пределов

Первый замечательный предел:

Второй замечательный предел:

Задача 2.

Теоретическое введение

Производная или от данной функции есть предел отношения приращения функции к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю: или

Механический смысл производной – скорость изменения функции.

Геометрический смысл производной – тангенс угла наклона касательной к графику функции:

Правила дифференцирования:

• Производная постоянной величины равна 0.
• Производная суммы равна сумме производных.
• Производная произведения:
• Производная частного:

Производная сложной функции:

Производная от сложной функции по независимому аргументу равна производной от по промежуточному аргументу , умноженной на его производною по независимой переменной .

Примеры:

• ;
• ;
• ;

Задача 4.

Найти неопределенные интегралы:

а) ;

Решение: введем переменную . Тогда ; . Сделаем замену:

.

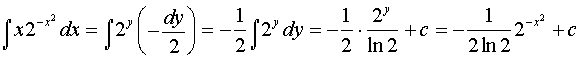б) ;

Решение: используем метод интегрирования по частям:

.

Обозначим: . Тогда .

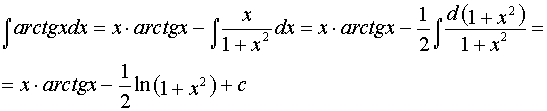
Задача 5.

Вычислить площадь фигуры, ограниченной линиями:

и .

Решение:

Найдем точки пересечения графиков данных функций. Для этого приравняем функции и решим уравнение

Итак, точки пересечения и .

Площадь фигуры найдем, используя формулу

.

В нашем случае

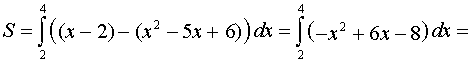
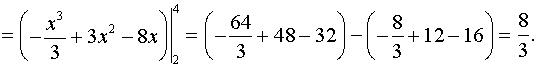
Ответ: площадь равна (квадратных единиц).

Примеры алгебраического сложения:

(3x) + (4x) = 7x(–3x) + (4x) = x(3x) + (–4x) = –x(–3x) + (–4x) = –7x(2x) + (2×2) = 2x + 2×2(–2x) + (2×2) = –2x + 2×2(2x) + (–2×2) = 2x — 2×2(–2x) + (–2×2) = –2x — 2×2(–3м) + (4м2) + (4n) = –3m + 4m2 + 4n(–3м) + (–4м2) + (4n) = –3м — 4м2 + 4n(–3м) + (4м2) + (–4n) = –3m — 4m2 — 4н(3м) + (4м2) + (4n) = 3м + 4м2 + 4n(2b2 + 4c + 3a3) + (5a + 3b + c2) = 5-я + 3-я3 + 3b + 2b2 + 4c + c2(–2b2 + 4c + 3a3) + (5a + 3b — c2) = 5-я + 3-я3 + 3b — 2b2 + 4c — c2(2b2 + 4c — 3a3) + (5a + 3b — c2) = 5–33 + 3b + 2b2 + 4c — c2(2b2 — 4c + 3a3) + (5a + 3b + c2) = 5-я + 3-я3 + 3b + 2b2 — 4c + c2(2b2 + 4c + 3a3) + (–5a + 3b + c2) = –5a + 3a3 + 3b + 2b2 + 4c + c2(–2b2 — 4c — 3a3) + (–5a — 3b — c2) = –5a — 3a3 — 3б — 2б2 — 4c — c2(4×2 + 6лет + 3лет2) + (х + 3 х2 + и2) = х + 7х2 + 6лет + 4лет2(–4×2 + 6лет + 3лет2) + (х + 3 х2 + и2) = х — х2 + 6лет + 4лет2(4×2 + 6лет + 3лет2) + (х — 3 х2 + и2) = х + х2 + 6лет + 4лет2(4×2 — от 6 лет до 3 лет2) + (х + 3 х2 + и2) = х + 7х2 — от 6 лет до 2 лет2(4×2 + 6лет + 3лет2) + (–X + 3 x2 — Y2) = — х + 7х2 + 6лет + 2лет2(–4×2 — от 6 лет до 3 лет2) + (–X — 3 x2 — Y2) = — х — 7×2 — от 6 лет до 4 лет2(х + у + 2z2) + (х + у + г2) = 2x + 2y + 3z2(х + у + 2z2) + (–X + y + z2) = 2у + 3z2(х — у + 2z2) + (–X + y + z2) = 3z2(х — у — 2z2) + (х + у + г2) = 2x — z2(–X + y + 2z2) + (х + у — г2) = 2y + z2(–X — y — 2z2) + (–X — y — z2) = — 2x — 2y — 3z2

Следуйте с:

Алгебраическое вычитание

Математические термины

Алгебра — это наука, изучающая действия над числовыми и буквенными величинами. Кроме того, она занимается решениями уравнений и связанными с ними действиями. Под буквенными величинами обычно понимают конкретные или переменные числовые значения. Входящие в состав записи буквы могут иметь различные числовые величины. Например, в формуле S * 4 + 12 символом S может быть заменена известная или неизвестная величина или даже целое выражение.

Математики под алгебраическим выражением понимают запись, составленную со смыслом, состоящую из букв и цифр, обозначающих числа. При этом она может содержать скобки и знаки арифметических действий. Исходя из этого простейшего определения можно утверждать, что формулы 2 * k — s, 4 * (y — 3/2), 0,89 * a — g * (9a + 4b), a2 и (29p — 56) / log (a + c) являются примерами алгебраических выражений. Так как буквы в записях обозначают различные числа, то их считают переменными, а само уравнение — выражением с переменной.

Если же значение переменной известно и его можно подставить на место буквенного обозначения, то результат, полученный после выполнения указанных в уравнении действий, называется ответом алгебраического выражения. Но если число, подставляемое вместо буквы, приводит к бессмысленности записи, то оно считается недопустимым. Из этого можно сделать вывод, что одна и та же алгебраическая запись при различных величинах букв может иметь отличные значения.

На практике приходится сталкиваться с довольно сложными и громоздкими алгебраическими выражениями, поэтому над ними приходится выполнять ряд действий, правил, законов или использовать свойства для упрощения записи.

Кроме определений здесь применяется понятие «тождественность». Под ним понимают два выражения, для которых при любых значениях переменных, входящих в их состав, будет справедливо их равенство, например, 56* (x+с) = 56 * x + 56 * с.

Правила сложения положительных и отрицательных чисел

Сложение положительных чисел — простой процесс. Для того, чтобы сложить два положительных числа, нужно их записать одно под другим, начиная с последнего разряда, и сложить соответствующие цифры.

Сложение отрицательных чисел тоже довольно простое. Для этого нужно записать числа друг под другом и сложить их, но уже с учетом знака чисел. Если оба числа отрицательные, то результат тоже будет отрицательным.

Но что делать, если нужно сложить положительное и отрицательное число? В этом случае нужно вычитать из большего числа меньшее по абсолютной величине. Знак результата определяется знаком числа с большей абсолютной величиной. Например, если нужно сложить -5 и 3, то нужно вычесть из 3 число 5 по абсолютной величине: 3 — 5 = -2. Результат будет отрицательным, так как число -5 имеет большую абсолютную величину.

Также стоит учитывать, что при сложении чисел разных знаков мы всегда берем модули этих чисел. Например, если нужно сложить -3 и 7, то мы берем модули этих чисел (т.е. превращаем их в положительные) и получаем 3 и 7. Затем вычитаем из большего числа меньшее по абсолютной величине: 7 — 3 = 4. Результат будет положительным, так как число 7 имеет большую абсолютную величину.

И помните, что правильное выполнение алгебраической суммы требует от нас тщательной работы, иначе результаты могут быть неверными.