Решение линейных уравнений с одной переменной

Содержание

В первая степень или линейные уравнения с неизвестным — это те, которые могут быть выражены как сумма двух членов следующим образом:

ах + Ь = 0

куда а и б, с участием к ≠ 0, являются действительными числами R или также комплексными C. Чтобы решить эту задачу, члены транспонируются, что означает изменение членов с одной стороны равенства на другую.

Чтобы решить неизвестное, транспонируется член + b, который должен перейти в правую часть равенства с измененным знаком.

топор = -b

Затем значение x очищается следующим образом:

х = — б / а

В качестве примера мы собираемся решить следующее уравнение:

6x — 5 = 4

Переносим член -5 в правую часть с измененным знаком:

6х = 4 + 5

Это эквивалентно добавлению 5 к обеим сторонам исходного уравнения:

6x — 5 + 5 = 4 + 5 → 6x = 9

А теперь решаем неизвестный «х»:

х = 9/6 = 3/2

Это эквивалентно делению обеих частей равенства на 6. Таким образом, мы можем использовать следующее, чтобы получить решение:

-Вы можете прибавить или вычесть одно и то же количество к обеим сторонам равенства в уравнении, не изменяя его.

-Вы также можете умножить (или разделить) на одинаковую величину все члены как слева, так и справа от уравнения.

-И если оба члена уравнения возведены в одну и ту же степень, равенство также не изменяется.

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

Для примера рассмотрим простейшее уравнение: x+3=5

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

1. Перенесем 6x из левой части в правую. Знак меняем на противоположный, то есть минус.

Приведем подобные и завершим решение.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12

1. Сократим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Алгоритм решения простого линейного уравнения
Раскрываем скобки, если они есть. Группируем члены, которые содержат неизвестную переменную в одну часть уравнения, остальные члены — в другую. Приводим подобные члены в каждой части уравнения. Решаем уравнение, которое получилось: aх = b. Делим обе части на коэффициент при неизвестном.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте схему-подсказку — храните ее в телефоне, учебники или на рабочем столе.

А вот и видео «Простейшие линейные уравнения» для тех, кто учиться в 5, 6 и 7 классе.

Разложение выражения на множители

Перечислим теперь некоторые наиболее распространённые приёмы разложения многочленов, как наиболее простых алгебраических функций, на множители.

Вынесение общего множителя за скобку

В том случае, когда все члены многочлена имеют один и тот же общий множитель, его можно вынести за скобку, получая тем самым разложение многочлена. Пример : Разложить на множители многочлен х 5 – 2х 3 +х 2 . Решение: Каждое слагаемое этого многочлена содержит множитель х 2 . Вынесем его за скобку и получим ответ:

х 5 – 2х 3 +х 2 = х 2 (х 3 – 2x + 1).

Применение формул сокращённого умножения

Формулы сокращения довольно эффективно применяются при разложении многочлена на множители. Полезно помнить следующие формулы:

1.Квадрат суммы двух величин равен квадрату первой плюс удвоенное произведение первой на вторую плюс квадрат второй.

2.Квадрат разности двух величин равен квадрату первой минус удвоенное произведение первой на вторую плюс квадрат второй.

3.Произведение суммы двух величин на их разность равно разности их квадратов.

4.Куб суммы двух величин равен кубу первой плюс утроенное произведение квадрата первой на вторую плюс утроенное произведение первой на квадрат второй плюс куб второй.

6. Произведение суммы двух величин на неполный квадрат разности равно сумме их кубов.

(a+b)(a 2 -ab+b 2 )=a 3 +b 3

7. Произведение разности двух величин на неполный квадрат суммы равно разности их кубов.

Пример: (3х+5) 2 =9х 2 +30х+25=0

Решение: используя формулу (1) 9х 2 +30х+25=(3х+5) 2

Применение выделения полного квадрата

Без преувеличения можно сказать, что метод выделения полного квадрата является одним из наиболее эффективных методов разложения на множители, применяемых при сдаче ГИА и ЕГЭ. Суть его состоит в выделении полного квадрата и последующего применения формулы разности квадратов. Поясним сказанное на примере. Пример : Разложить на множители многочлен x4 + 4×2 – 1. Решение : Имеем х 4 +4х 2 −1=х 4 +2

х 2х 22х 2
х 2

Теоретический материал

Алгебра

Глава 6. Линейные уравнения

6.5. Линейное уравнение с одним неизвестным

Ученик

Что такое линейное уравнение с одним неизвестным?

Учитель

Такое уравнение представляет собой равенство двух линейный функций. Любое уравнение первой степени с одним неизвестным можно представить в виде , где — неизвестное, коэффициент и свободный член — любые действительные числа.

Пример

В уравнении перенесем все члены правой части в левую: , а затем приведем подобные члены: . Уравнение равносильно уравнению , и оба они имеют одни и те же корни.

Ученик

А как же оно решается?

Определение

называют нормальной формой линейного уравнения с одним неизвестным.

Учитель

Решается оно (если /span>) так: , .При любом действительном значении уравнение в этом случае имеет корень, причем единственный. Если и , то получаем уравнение , которому не удовлетворяют никакие значения , т. е. оно не имеет ни одного корня.Если и , то уравнение обращается в тождество при любых значениях , т. е. имеет бесконечное множество корней .

Примечание. При решении вопроса равносильности уравнений учитываем лишь действительные их корни.

Учитель

Чтобы найти корень данного уравнения, надо заменять его более простыми и равносильными ему уравнениями до тех пор, пока не получится уравнение вида , где — неизвестное данного уравнения, — некоторое число. Уравнение равносильно данному уравнению, которое также имеет корень .

Ученик

Так, не совсем понятно… Как именно можно преобразовывать уравнение?

Учитель

Решение уравнения выполняется обычно но схеме, состоящей из следующих этапов (первый и второй иногда удобнее переставлять и не в каждом уравнении нужно выполнять все пять этапов): 1) сделать все коэффициенты уравнения целыми, умножив все члены обеих его частей на наименьшее общее кратное всех знаменателей (согласно следствию 3, полученное при этом уравнение равносильно данному уравнению);2) раскрыть скобки (при этом каждая часть уравнения преобразуется в тождественно равную ей и поэтому полученное уравнение равносильно предыдущему и данному уравнениям); 3) перенести члены с неизвестным из правой части в левую, а известные члены из левой части в правую (по следствию 2 получаем уравнение, равносильное предыдущему, а поэтому и данному);4) привести подобные члены в каждой часто уравнения (тождественное преобразование не нарушает равносильности) ;5) разделить обе части уравнения на коэффициент при неизвестном, если он не нуль (по следствию 4 полученное уравнение равносильно предыдущему, а поэтому — и данному уравнению).

Ученик

О, я знаю! Полученное при этом значение неизвестного является искомым корнем данного уравнения.

Учитель

Правильно, ты молодец! А еще, если подставить этот корень в данное уравнение вместо неизвестного и выполнить указанные в уравнении действия, то в левой и правой частях должно получиться одно и то же число.

Ученик

А если получится неверное равенство?

Учитель

Если же получится неверное равенство, то в решении была допущена ошибка, которую надо найти и устранить. Это называется проверкой решения уравнения.

Учитель

Главное значение уравнений состоит в том, что они дают наиболее удобный способ решения задач. Даже те задачи, которые в арифметике решаются сложно, в алгебре при помощи уравнений решаются значительно проще.

Ученик

Как же составлять уравнения по условию задачи?

Учитель

Составление уравнения по условию задачи выполняется по следующей схеме: 1) выбираем неизвестное (обычно лучше то, которое в задаче требуется найти, хотя можно и другое) и обозначаем его буквой (например, ); 2) выражаем другие величины, о которых говорится в задаче, через и данные в задаче числа (получаем функции от );3) составляем уравнение, приравнивая две из полученных функций от или одну из функций и число, которые по условию задачи или по зависимости между величинами должны быть равны;4) решаем уравнение;5) получаем ответ на вопрос задачи (если корней несколько, то все ли они могут удовлетворить условию задачи; если в задаче требуется найти несколько чисел, то находим остальные; если через было обозначено вспомогательное неизвестное, то находим число, которое требуется определить в задаче);6) проверка решения и ответа по условию задачи.

Ученик

Кажется понятно.

Учитель

Ты молодец!

§ Решение простых уравнений 5 класс

Решение простых уравнений 5 класс
Решение сложных (составных) уравнений

Запомните!

Уравнение — это равенство, содержащее букву, значение которой надо найти.

В уравнениях неизвестное обычно обозначается строчной латинской буквой. Чаще всего используют буквы
«x» и «y» .

• Корень уравнения — это значение буквы, при котором из уравнения получается верное числовое равенство.
• Решить уравнение — значит найти все его корни или убедиться, что корней нет.

Запомните!

Решив уравнение, всегда после ответа записываем проверку.

Информация для родителей

Уважаемые родители, обращаем ваше внимание на то, что в начальной школе и в 5 классе дети НЕ знают тему
«Отрицательные числа». Не пытайтесь объяснить решение уравнений через перенос чисел и букв
из одной части уравнения в другую с изменением знака

Не пытайтесь объяснить решение уравнений через перенос чисел и букв
из одной части уравнения в другую с изменением знака.

Освежить знания по понятиям, связанным со сложением, вычитанием, умножением и делением вы можете в уроке
«Законы арифметики».

Решение уравнений на сложение и вычитание

Как найти неизвестноеслагаемое x + 9 = 15	Как найти неизвестноеуменьшаемое x − 14 = 2	Как найти неизвестноевычитаемое 5 − x = 3
Чтобы найти неизвестное слагаемое, надо от суммы отнять известное слагаемое.	Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.	Чтобы найти неизвестное вычитаемое, надо от уменьшаемого отнять разность.
x + 9 = 15x = 15 − 9x = 6Проверка 6 + 9 = 1515 = 15	x − 14 = 2x = 14 + 2x = 16Проверка 16 − 2 = 1414 = 14	5 − x = 3x = 5 − 3x = 2Проверка 5 − 2 = 33 = 3

Решение уравнений на умножение и деление

Как найти неизвестныймножитель y · 4 = 12	Как найти неизвестноеделимое y : 7 = 2	Как найти неизвестныйделитель 8 : y = 4
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.	Чтобы найти неизвестное делимое, надо частное умножить на делитель.	Чтобы найти неизвестный делитель, надо делимое разделить на частное.
y · 4 = 12y = 12 : 4y = 3Проверка 3 · 4 = 1212 = 12	y : 7 = 2y = 2 · 7y = 14Проверка 14 : 7 = 22 = 2	8 : y = 4y = 8 : 4y = 2Проверка 8 : 2 = 44 = 4

Решение простых уравнений 5 класс
Решение сложных (составных) уравнений

Ключевые моменты

Ключевые выводы следующие:

• Знать алгоритм решения линейных уравнений.
• Умение раскрывать скобки.
• Не стоит переживать, если где-то у вас появляются квадратичные функции, скорее всего, в процессе дальнейших преобразований они сократятся.
• Корни в линейных уравнениях, даже самых простых, бывают трех типов: один единственный корень, вся числовая прямая является корнем, корней нет вообще.

Надеюсь, этот урок поможет вам освоить несложную, но очень важную для дальнейшего понимания всей математики тему. Если что-то непонятно, заходите на сайт, решайте примеры, представленные там. Оставайтесь с нами, вас ждет еще много интересного!

Линейное уравнение с одной переменной имеет общий видax
+ b
= 0.
Здесь x
— это переменная, a
и b
– коэффициенты. По-другому a
называют «коэффициент при неизвестной», b
– «свободный член».

Коэффициенты это какие-то числа, а решить уравнение — это значит найти значение x
, при котором выражение ax
+ b
= 0 верно. Например, имеем линейное уравнение 3x
– 6 = 0. Решить его – это значит найти, чему должен быть равен x
, чтобы 3x
– 6 было равно 0. Выполняя преобразования, получим:
3x
= 6x
= 2

Таким образом выражение 3x
– 6 = 0 верно при x
= 2:
3 * 2 – 6 = 0
2 – это корень данного уравнения
. Когда решают уравнение, то находят его корни.

Коэффициенты a
и b
могут быть любыми числами, однако бывают такие их значения, когда корень линейного уравнения с одной переменной не один.

Если a
= 0, то ax + b
= 0 превращается в b
= 0. Здесь x
«уничтожается». Само же выражение b
= 0 может быть истинным только в том случае, если знание b
– это 0. То есть уравнение 0*x
+ 3 = 0 неверно, т. к. 3 = 0 – это ложное утверждение. Однако 0*x
+ 0 = 0 верное выражение. Отсюда делается вывод, если a
= 0 и b
≠ 0 линейное уравнение с одной переменной корней не имеет вообще, но если a
= 0 и b
= 0, то корней у уравнения бесконечное множество.

Если b
= 0, а a
≠ 0, то уравнение примет вид ax
= 0. Понятно, что если a
≠ 0, но в результате умножения получается 0, то значит x
= 0. То есть корнем этого уравнения является 0.

Если же ни a
, ни b
не равны нулю, то уравнение ax + b
= 0 преобразовывается к видуx = –b / a
.
Значение x
в данном случае будет зависеть от значений a
и b
. При этом оно будет одним единственным. То есть нельзя при одних и тех же коэффициентах получить два или более разных значений x
. Например,
–8.5x
– 17 = 0x
= 17 / –8.5x
= –2
Никакое другое число, кроме –2 нельзя получить, деля 17 на –8.5.

Бывают уравнения, которые с первого взгляда непохожи на общий вид линейного уравнения с одной переменной, однако легко преобразуются к нему. Например,
–4.8 + 1.3x
= 1.5x
+ 12

Если перенести все в левую часть, то в правой останется 0:
–4.8 + 1.3x
– 1.5x
– 12 = 0

Теперь уравнение приведено к стандартному виду и можно его решить:x
= 16.8 / 0.2x
= 84

\(x=\)

Это число и будет корнем.

То есть, мы преобразовываем уравнение, делая его с каждым шагом все проще, до тех пор, пока не сведем к совсем примитивному уравнению «икс = число», где корень – очевиден. Наиболее часто применяемыми при решении линейных уравнений являются следующие преобразования:

Например
: прибавим \(5\) к обеим частям уравнения \(6x-5=1\)

\(6x-5=1\) \(|+5\)
\(6x-5+5=1+5\)
\(6x=6\)

Обратите внимание, что тот же результат мы могли бы получить быстрее – просто записав пятерку с другой стороны уравнения и поменяв при этом ее знак. Собственно, именно так и делается школьный «перенос через равно со сменой знака на противоположный»

2. Умножение или деление обеих частей уравнения на одинаковое число или выражение.

Например
: разделим уравнение \(-2x=8\) на минус два

\(-2x=8\) \(|:(-2)\)
\(x=-4\)

Обычно данный шаг выполняется в самом конце, когда уравнение уже приведено к виду \(ax=b\), и мы делим на \(a\), чтобы убрать его слева.

Прибавляем \(2x\) слева и справа

Вычитаем \(24\) из обеих частей уравнения

Опять приводим подобные слагаемые

Теперь делим уравнение на \(-3\), тем самым убирая перед иксом в левой части.

Ответ

: \(7\)

Ответ найден. Однако давайте его проверим. Если семерка действительно корень, то при подстановке ее вместо икса в первоначальное уравнение должно получиться верное равенство — одинаковые числа слева и справа. Пробуем.

Проверка:

\(6(4-7)+7=3-2\cdot7\)
\(6\cdot(-3)+7=3-14\)
\(-18+7=-11\)
\(-11=-11\)

Сошлось. Значит, семерка и в самом деле является корнем исходного линейного уравнения.

Остается вопрос – а как определить, что делать с уравнением на очередном шаге? Как именно его преобразовывать? Делить на что-то? Или вычитать? И что конкретно вычитать? На что делить?

Ответ прост:

Урок «Уравнения с двумя неизвестными»

Бесплатно

Большинство задач в математике ориентировано на решение стандартных уравнений, содержащих одну переменную. Иногда используется система двух и более уравнений, которые могут включать, соответственно, две и более переменные.

Однако изучим отдельное уравнение, содержащее в своем составе помимо числовых выражений два неизвестных абстрактных выражения. Например:

х2 + 2у = 6

Любое подобное уравнение называется уравнением с двумя переменными. Решением подобного уравнения называется такая пара значений х и у, при которой все выражение преобразуется в равносильное правильное равенство. Используем такие значения для переменных:

• х = 2
• у = 1
• Подставляя в наше уравнение, получим верное равенство:
• х2 + 2у = 6
• (2)2 + 2(1) = 6
• 4 + 2 = 6
• Таким образом, пара чисел (2, 1) являются решением для уравнения.

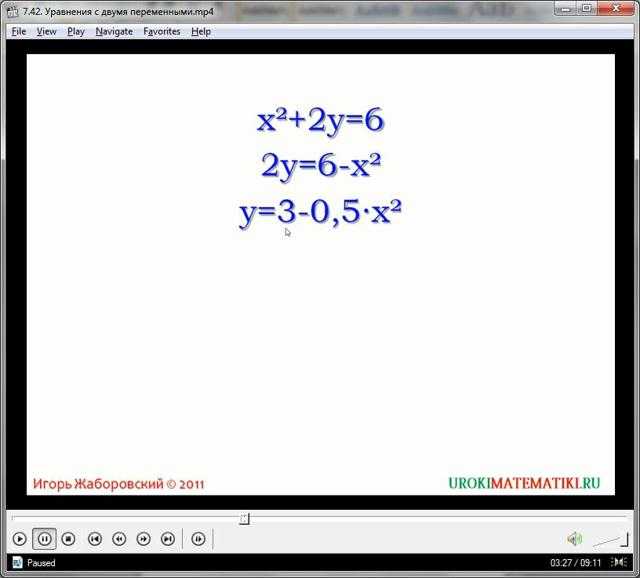
х2 + 2у = 6. Отметим, что при записи решения необходимо указывать значения переменных в скобках через запятую, на первое место записывая значение х (это не строго, но утверждено).

1. Решая первый пример методом подбора, легко найти ещё одну пару решений – например, воспользуемся значениями (4, -5):
2. х2 + 2у = 6
3. (4)2 + 2(-5) = 6
4. 16 – 10 = 6
5. Пара чисел превратила уравнение в правильное равенство, значит, она так же соответствует решению данного уравнения.

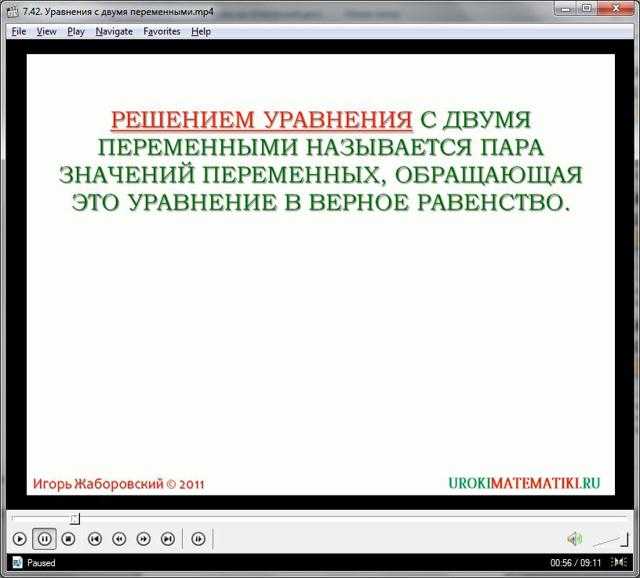
Как можно понять из видеоурока, уравнение с двумя переменными имеет множество решений, точнее, множество пар чисел, которые будут соответствовать критериям правильного ответа. Преобразуем первое уравнение следующим образом. Поделим все части равенства на 2:

• х2 + 2у = 6
• 0,5х2 + у = 3
• у = 3 – 0,5х2
• Полученное выражение у = 3 – 0,5х2 является ничем иным, как функцией – зависимостью одной переменной от второй. Иначе говоря:
• у = 3 – 0,5х2
• у = f(х)
• f(х) = 3 – 0,5х2

Как мы помним из видеоуроков, посвященных основам функций, любая зависимость характеризуется тремя элементами: множеством неких начальных аргументов, формулой преобразования, множеством полученных значений.

В нашем уравнении множество всех реальных решений представлено парами значений х и у – то есть, парными элементами обеих множеств функции. При этом само уравнение представляет собой выражение зависимости между первой и второй переменной.

Помимо того, выражение у = 3 – 0,5х2 имеет точно такие же пары решений, как и х2 + 2у = 6 – поэтому, эти уравнения называются равносильными. Равносильные уравнения получаются в таких случаях:

1.      При осуществлении переноса слагаемых (с учетом инверсии знака) с одной части равенства в другую;
2.      При различных тождественных преобразованиях, не меняющих смысл равенства;
3.      При умножении или делении одновременно обеих частей уравнения на один и тот же коэффициент;

Важно понимать, что, осуществляя различные преобразования в уравнении, нельзя искажать область определения какой-либо из переменных. Большинство тождественных преобразований сохраняют неизменным множество х или у, но бывают неприятные исключения

Рассмотрим такой пример:

у = х(2/(х) + 4)

Для решения этого уравнения логичнее было бы раскрыть скобки: совершить вполне тождественное преобразование, которое почти никогда не затрагивает область определения переменных.

Но в данном случае раскрытие скобок не будет тождественным явлением.

В изначальном варианте представленное уравнение имеет множество решений х, исключая х = 0, так как при данном значении одночлен 2/х потеряет смысл вместе со всем уравнением. Если же мы раскроем скобки, то получим следующее:

у = х(2/(х) + 4) = 2х/х + 4х = 2 + 4х

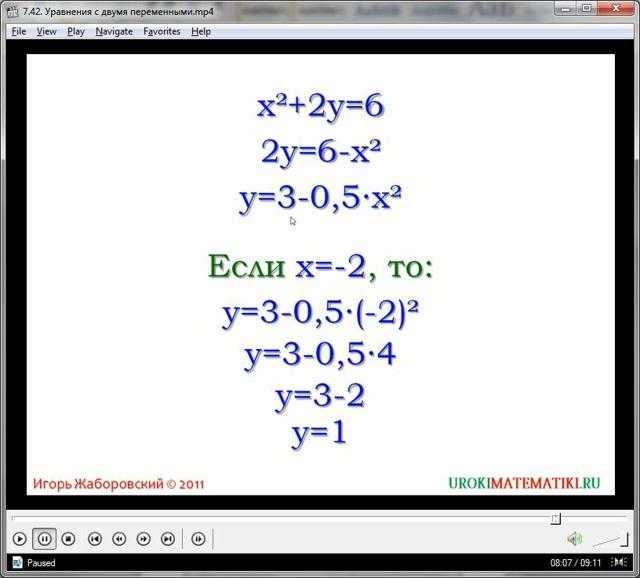
Как легко заметить, в новом уравнении область определения х является бесконечной, включая х = 0. То есть, множество значений х изменилось, уравнение не является равносильным заданному примеру. Тем не менее, часто подобные упражнения решают обычными преобразованиями. Просто нужно совершать подстановочную проверку, что бы исключить недействительные решения уравнения.

Подавляющее большинство уравнений с двумя переменными преобразуется в аналитические зависимости, после чего совершается подстановка любых двух значений х и вычисляется, таким образом, пара решений х и у. При этом, самих решений, как правило, бесконечное множество. Но есть и небольшие исключения – когда из области определения переменной выпадает какая-либо точка.

Некоторые уравнения с двумя неизвестными имеют только одно решение, например, выражение х2 + у2 = 0 имеет только одну пару корня – (0, 0). А уравнение вида х2 + у2 = -1 не имеет действительных решений вообще.

То же справедливо по отношению к любым подобным уравнениям, которые равны отрицательным числам – ведь квадраты, как и их суммы, в принципе не могут дать отрицательных значений.

Неравенства, сводящиеся к линейным

Огромное количество неравенств с помощью равносильных преобразований можно заменить равносильным линейным неравенством, другими словами, свести к линейному неравенству. Такие неравенства называют неравенствами, сводящимися к линейным.

В школе почти одновременно с решением линейных неравенств рассматривают и несложные неравенства, сводящиеся к линейным. Они представляют собой частные случаи целых неравенств, а именно в их левой и правой части находятся целые выражения, которые представляют собой или линейные двучлены, или преобразуются к ним путем раскрытия скобок и приведения подобных слагаемых. Для наглядности приведем несколько примеров таких неравенств: 5−2·x>0, 7·(x−1)+3≤4·x−2+x, .

Неравенства, которые подобны по виду указанным выше, всегда можно свести к линейным. Это можно сделать путем раскрытия скобок, приведения подобных слагаемых, перестановки слагаемых местами и переноса слагаемых из одной части неравенства в другую с противоположным знаком.

Например, чтобы свести неравенство 5−2·x>0 к линейному, достаточно переставить слагаемые в его левой части местами, имеем −2·x+5>0. Для сведения второго неравенства 7·(x−1)+3≤4·x−2+x к линейному нужно немного больше действий: в левой части раскрываем скобки 7·x−7+3≤4·x−2+x, после этого приводим подобные слагаемые в обеих частях 7·x−4≤5·x−2, дальше переносим слагаемые из правой части в левую 7·x−4−5·x+2≤0, наконец, приводим подобные слагаемые в левой части 2·x−2≤0. Подобным образом и третье неравенство можно свести к линейному неравенству.

Из-за того, что подобные неравенства всегда можно свести к линейным, некоторые авторы даже называют их тоже линейными. Но все же будем их считать сводящимися к линейным.

Теперь становится понятно, почему подобные неравенства рассматривают вместе с линейными неравенствами. Да и принцип их решения абсолютно такой же: выполняя равносильные преобразования, их можно привести к элементарным неравенствам, представляющим собой искомые решения.

Чтобы решить неравенство подобного вида можно его предварительно свести к линейному, после чего решить это линейное неравенство. Но рациональнее и удобнее поступать так:

• после раскрытия скобок собрать все слагаемые с переменной в левой части неравенства, а все числа – в правой,
• после чего привести подобные слагаемые,
• а дальше – выполнить деление обеих частей полученного неравенства на коэффициент при x (если он, конечно, отличен от нуля). Это даст ответ.

Пример.

Решите неравенство 5·(x+3)+x≤6·(x−3)+1.

Решение.

Сначала раскроем скобки, в результате придем к неравенству 5·x+15+x≤6·x−18+1. Теперь приведем подобные слагаемые: 6·x+15≤6·x−17. Дальше переносим слагаемые с левую часть, получаем 6·x+15−6·x+17≤0, и снова приводим подобные слагаемые (что приводит нас к линейному неравенству 0·x+32≤0) и имеем 32≤0. Так мы пришли к неверному числовому неравенству, откуда делаем вывод, что исходное неравенство не имеет решений.

Ответ:

нет решений.

В заключение отметим, что существует и масса других неравенств, сводящихся к линейным неравенствам, или к неравенствам рассмотренного выше вида. Например, решение показательного неравенства 52·x−1≥1 сводится к решению линейного неравенства 2·x−1≥0. Но об этом будем говорить, разбирая решения неравенств соответствующего вида.

Список литературы.

• Алгебра: учеб. для 8 кл. общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.
• Алгебра: 9 класс: учеб. для общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2009. — 271 с. : ил. — ISBN 978-5-09-021134-5.
• Мордкович А. Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 11-е изд., стер. — М.: Мнемозина, 2009. — 215 с.: ил. ISBN 978-5-346-01155-2.
• Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 13-е изд., стер. — М.: Мнемозина, 2011. — 222 с.: ил. ISBN 978-5-346-01752-3.
• Мордкович А. Г. Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А. Г. Мордкович, П. В. Семенов. — 2-е изд., стер. — М.: Мнемозина, 2008. — 287 с.: ил. ISBN 978-5-346-01027-2.

Линейные системы уравнений

Системы линейных уравнений. Метод подстановки 

+ показать

• Выражаем одну переменную через другую.

• Выраженную из одного уравнения переменную подставляем во второе уравнение. Получаем уравнение относительно одной переменной, которое и решаем.

• Опираясь на найденное значение одной переменной, находим значение второй, подставляя в оставшееся уравнение.

Решение: + показать

Из первого уравнения системы выражаем через и подставляем во второе уравнение:

Вторая строка системы – уравнение с одной переменной. Решаем его и найденное значение подставляем в первое уравнение для нахождения .

Ответ:

Системы линейных уравнений. Метод сложения 

• + показать
• • Добиваемся, путем равносильных преобразований, наличия равных (или противоположных) коэффициентов при одной из неизвестных переменных в уравнениях.
• • Вычитаем (или складываем) полученные уравнения с целью выхода на уравнение с одной неизвестной. 
• • Решаем  полученное уравнение с одной неизвестной.
• • Найденное значение одной переменной подставляем в любое из уравнений системы, находим значение второй.

1. 1. Решить систему уравнений: 
2. Решение: + показать
3. Складываем уравнения системы, заменяя результатом одно из уравнений, оставляя другое.

Ответ:  

• 2. Решить систему уравнений: 
• Решение: + показать

Прежде домножаем первую строку системы , вторую строку системы – на . Вычитаем уравнения системы, заменяя результатом одно из уравнений, оставляя другое.

1. Ответ:  

Системы уравнений, сводящихся к линейным

• 1. Решить систему уравнений: 
• Решение: + показать
• Можно сделать замену и Тогда выходим на систему линейных уравнений:
• Систему можно решить методом сложения, например.
• Но приведем решение без замены.
• Умножим первое уравнение системы на , второе – на и произведем сложение полученных уравнений, оставим при этом в системе, например, первое уравнение исходной системы.
• Ответ:  

1. 2.
    Решить систему уравнений: 
2. Решение: + показать
3. Можно сделать замену и выйти на систему линейных уравнений:
4. Приведем решение без замены.
5. Выражаем из второго уравнения системы и подставляем в первое.
6. Ответ:  

Нелинейные системы уравнений. Метод подстановки

• Решить систему уравнений: 
• Решение: + показать
• Выражаем из первого уравнения системы и подставляем во второе.
• Ответ:  

Нелинейные системы уравнений. Метод сложения

1. Решить систему уравнений: 
2. Решение: + показать
3. Складываем уравнения системы, заменяя результатом одно из уравнений, оставляя другое.
4. Ответ:  

Нелинейные системы уравнений. Метод почленного умножения (деления)

• 1. Решить систему уравнений: 
• Решение: + показать
• Производим деление первой строки на вторую, оставляем в системе вторую строку без изменений.
• Ответ:  
• Симметрические системы. Метод введения переменной

Симметрическая система – система, все уравнения которой симметрические.

Симметрическое уравнение от двух переменных и – уравнение, которое не изменяется при замене на и на .

1. Для таких систем удобно использовать замену  
2. Решить систему уравнений: 
3. Решение: + показать
4. При замене  приходим к следующей системе
5.  которую будем решать способом подстановки:
6. Производим обратную замену:
7. Ответ:
8. Системы однородных уравнений и приводящиеся к ним системы
9. Однородным уравнением с двумя неизвестными  будем называть уравнение вида
10. 1. Решить систему уравнений: 
11. Решение: + показать

Первое уравнение системы – однородное. Производим деление первого уравнения системы на (можно и на или ). Заметим, опасности деления на ноль нет.

• Первое уравнение системы – квадратное относительно .
• Ответ:
• 2. Решить систему уравнений: 
• Решение: + показать

Применим прежде к системе метод сложения. После чего выйдем на однородное уравнение.

1. Ответ:

Графический метод решения систем уравнений

• 1. Решите графически систему уравнений: 
• Решение: + показать
• Выразим в обеих строках системы через :

Первое уравнение системы задает прямую, второе – гиперболу. Строим графики в одной системе координат, находим координаты точек пересечения графиков.

1. Ответ: 
2. 2. Решите графически систему уравнений: 
3. Решение: + показать

Первая строка системы задает окружность с центром в точке радиусом .  Вторая строка системы задает прямую .

• Находим координаты точек пересечения графиков:
• Ответ: 
• 3. Решите графически систему уравнений: 
• Решение: + показать
• Первая строка системы задает параболу с ветвями вверх с вершиной в точке .
• Так как , то из второй строки системы при условии, что То есть вторая строка системы задает прямую с выколотой точкой 
• Ответ: 
• Задания для самостоятельной работы
• + показать
• Решите системы уравнений:
• 1.
• Ответ:
• 2. 
• Ответ:
• 3. 
• Ответ:
• 4. 
• Ответ:
• 5. 
• Ответ:
• 6. 
• Ответ:
• 7. 
• Ответ:
• 8. 
• Ответ:
• Решите графически системы уравнений:
• 9. 
• Ответ:
• 10. 
• Ответ:
• egeMax |

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Печать страницы

Практическое применение линейных уравнений

Линейные уравнения находят широкое применение во многих областях науки, техники и экономики. Они позволяют моделировать и решать разнообразные задачи, описывающие зависимости между различными величинами.

Одним из практических применений линейных уравнений является решение задач финансового планирования. Например, линейное уравнение может использоваться для определения оптимального распределения бюджета между различными проектами или для определения точки безубыточности предприятия.

Линейные уравнения также широко используются в физике для описания физических законов. Например, закон Ома в электротехнике может быть выражен линейным уравнением, которое связывает напряжение, силу тока и сопротивление электрической цепи.

В экономической теории линейные уравнения используются для моделирования спроса и предложения на товары, определения равновесной цены и количества товаров на рынке. Также они могут быть использованы для определения оптимальной стратегии производства и распределения ресурсов.

Еще одно практическое применение линейных уравнений — задачи геометрии и механики. Например, линейные уравнения могут быть использованы для описания движения материальной точки или для определения геометрических характеристик фигур.

Кроме того, линейные уравнения имеют важное значение в статистике, эконометрике и исследовании операций. Они позволяют анализировать и моделировать статистические данные, прогнозировать будущие значения и оптимизировать различные процессы

В заключение, линейные уравнения — это мощный инструмент, который позволяет решать разнообразные практические задачи. Они применяются в различных областях науки и техники для моделирования и оптимизации процессов, а также для анализа данных и прогнозирования будущих значений.