Высшая алгебра практический и немного теоретический курс для начинающих

Векторные пространства и линейные преобразования

6.1. Векторное (линейное) пространство. Так что же такое вектор?6.2. Основные понятия векторного пространства6.3. Евклидово пространство. Длина и угол

6.4. Линейные преобразования6.4.1. Как записать оператор в матричной форме?6.4.2. Матрица линейного преобразования в различных базисах

6.5. Собственные числа и собственные векторы линейного преобразования6.5.1. Как найти собственные значения и собственные векторы?6.5.2. Линейное преобразование в базисе из собственных векторов6.5.3. Сколько у матрицы собственных чисел и собственных векторов?6.5.4. Как решать задачу в случае кратных собственных чисел?

7. Решения и ответы, а также Приложения доступны в полной версии.

Полную и свежую версию этой книги в pdf-формате можно найти здесь.

Также вы можете – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Aлeксaндр Eмeлин

Основные понятия алгебры

Алгебра — это раздел математики, который изучает математические структуры и операции, связанные с ними. Она изучает свойства и правила операций над числами, а также их обобщения на другие объекты.

Арифметические операции — это основные операции, которые выполняются над числами в алгебре. Включают в себя сложение (+), вычитание (-), умножение (*) и деление (/).

Переменная — это символ, который представляет неизвестное число или значение в алгебре. В алгебре переменные часто обозначаются буквами, например, «x» или «y».

Терм — это элементарное выражение или член алгебраического выражения, который может быть числом, переменной или их произведением. Например, в алгебраическом выражении «3x + 2y», термины это «3x» и «2y».

Алгебраическое выражение — это выражение, состоящее из переменных, констант, операций и скобок. Оно может быть как простым, так и сложным. Примеры алгебраических выражений: «2x + 3», «x^2 — 5x + 2».

Уравнение — это математическое выражение, в котором два алгебраических выражения разделяются знаком равенства (=). Оно позволяет находить значения переменных, удовлетворяющие условиям уравнения. Пример уравнения: «2x + 5 = 10».

Система уравнений — это набор уравнений, которые рассматриваются вместе. Решение системы уравнений находит значения переменных, которые удовлетворяют всем уравнениям системы. Пример системы уравнений:

• 2x + y = 10
• x — y = 2

Функция — это отображение или правило, которое связывает каждое значение из одного множества (аргумент) со значением из другого множества (значение функции). Функции используются для описания зависимостей между переменными. Пример функции: «f(x) = 2x + 3».

Матрица — это таблица чисел, расположенных в определенном порядке. Матрицы используются для представления данных и решения систем уравнений. Они имеют размерность, определяемую количеством строк и столбцов. Пример матрицы:

1	2
3	4

Линейная функция — это функция вида f(x) = mx + b, где m и b — числа. Они описывают прямую линию на графике и используются для решения многих задач в алгебре.

Показательная функция — это функция вида f(x) = a^x, где a — база показательной функции. Она описывает экспоненциальный рост или убывание и широко используется в науке и экономике.

Квадратное уравнение — это уравнение вида ax^2 + bx + c = 0, где a, b и c — числа, а x — переменная. Оно имеет вид параболы на графике и может иметь два, один или ни одного решения.

Это лишь некоторые из основных понятий алгебры. Алгебра имеет дополнительные термины и концепции, которые используются для более сложных и глубоких исследований.

Наибольшее и наименьшее значения функции на данном отрезке

Чтобы найти наибольшее и наименьшее значения функции y=f (x) на отрезке , нужно найти значения этой функции на концах отрезка и в тех критических точках, которые принадлежат данному отрезку, а затем из всех полученных значений выбрать наибольшее и наименьшее.

Схема исследования функции.

1) область определения D (f); 2) четность (нечетность); периодичность; 3) точки пресечения графика с осями координат; 4) промежутки знакопостоянства; 5) промежутки возрастания и убывания; 6) точки экстремума и значения функции в этих точках; 7) поведение функции в окрестности каждой «особой» точки и при больших по модулю значениях х.

Корень n-й степени.

Неотрицательное значение корня n-й степени из неотрицательного числа называется арифметическим корнем.

Свойства корня n-й степени.

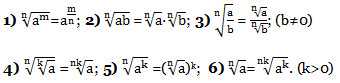
Прямая на плоскости

• Общее уравнение прямой: Ax+By+C=0.
•  Уравнение прямой с  угловым коэффициентом: y=kx+b  (k – угловой коэффициент).
• Острый угол между прямыми y=k₁x+b₁ и y=k₂x+b₂ определяется по формуле:

• k₁=k₂ — условие параллельности  прямых y=k₁x+b₁  и  y=k₂x+b_2.
• Условие перпендикулярности этих же прямых:

Уравнение прямой, имеющей угловой коэффициент k, и проходящей

через точку М(х₁; у₁), имеет вид: у-у₁=k (х-х₁).

Уравнение прямой, проходящей через две данные точки (х1; у1) и (х2; у2) имеет вид:

Длина отрезка М1М2 с концами в точках М1(х1; у1) и М2(х2; у2):

Координаты точки М(хо; уо) – середины отрезка М1М2

Координаты точки С(х; у), делящей  в заданном отношении λ отрезок М1М2  между точками М1(х1; у1) и М2(х2; у2):

Расстояние от точки М(хо; уо) до прямой ax+by+c=0:

Уравнения с одним неизвестным

Основная теорема алгебры

Уравнение N-го порядка имеет, по меньшей мере, один корень в поле комплексных чисел.
Следствием из данной теоремы является утверждение о том, что уравнение N-го порядка имеет ровно N корней с учётом их кратности.

ax+b=,a≠{\displaystyle ax+b=0,\quad a\neq 0}

Имеют единственный корень x=−ba{\displaystyle x=-b/a}

Квадратные уравнения

ax2+bx+c=,a≠{\displaystyle ax^{2}+bx+c=0,\quad a\neq 0.}

Корни определяются формулой при D>{\displaystyle D>0}
x1,2=−b±b2−4ac2a{\displaystyle x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}

Корни определяются формулой при D={\displaystyle D=0} x1=x2=−b2a{\displaystyle x_{1}=x_{2}=-{\frac {b}{2a}}}

Корни определяются формулой при D<{\displaystyle D<0} x1,2=−b±i|D|2a.{\displaystyle x_{1,2}={\frac {-b\pm i{\sqrt {|D|}}}{2a}}.}

Есть ещё один способ рещения квадратных уравнений при a=1{\displaystyle a=1}. Для этого используется теорема Виета.

x2+px+q={\displaystyle x^{2}+px+q=0}

{x1+x2=−p;x1x2=q;{\displaystyle {\begin{cases}x_{1}+x_{2}=-p;\\x_{1}x_{2}=q;\end{cases}}}

Подобрать устно числа, удовлетворяющие этим уравнениям, поможет прямая теорема. С её помощью можно определить знаки корней, не зная сами корни. Для этого следует руководствоваться правилом:

1)если свободный член отрицателен, то корни имеют различный знак, и наибольший по модулю из корней — знак, противоположный знаку второго коэффициента уравнения;

2)если свободный член положителен, то оба корня обладают одинаковым знаком, и это — знак, противоположный знаку второго коэффициента.

Часные случаи:

1.ax2+bx+c=,c={\displaystyle ax^{2}+bx+c=0,c=0.}

x(ax+b)={\displaystyle x(ax+b)=0}

x={\displaystyle x=0} или ax+b={\displaystyle ax+b=0}

2.ax2+bx+c=,b={\displaystyle ax^{2}+bx+c=0,b=0.}

ax2=−c{\displaystyle ax^{2}=-c}

x1,2=±−ca{\displaystyle x_{1,2}=\pm {\sqrt {-c/a}}}

3.ax2+bx+c=,b=,c={\displaystyle ax^{2}+bx+c=0,b=0,c=0.}

ax2={\displaystyle ax^{2}=0}

x2={\displaystyle x^{2}=0}

x={\displaystyle x=0}

Биквадратные уравнения

ax4+bx2+c=,a≠{\displaystyle ax^{4}+bx^{2}+c=0,\quad a\neq 0.}

Подстановкой y=x2{\displaystyle y=x^{2}} сводятся к квадратному уравнению

ay2+by+c={\displaystyle ay^{2}+by+c=0.}

Кубические уравнения

ax3+bx2+cx+d=,a≠{\displaystyle ax^{3}+bx^{2}+cx+d=0,\quad a\neq 0.}
При вещественных коэффициентах a, b, c, d имеют хотя бы один вещественный корень.
Для нахождения точных значений корней в радикалах может быть использована формула Кардано.
Однако вычисления по этому методу довольно громоздки.

Если уравнение имеет рациональный корень x1{\displaystyle x_{1}}, можно подобрать его и далее, разделив левую часть исходного уравнения на двучлен x−x1{\displaystyle x-x_{1}}, свести уравнение к квадратному.

Уравнения высших степеней

anxn+an−1xn−1+…+a1x+a=,an≠{\displaystyle a_{n}x^{n}+a_{n-1}x^{n-1}+…+a_{1}x+a_{0}=0,\quad a_{n}\neq 0.}

Уравнения 5-го порядка и выше в общем случае неразрешимы в радикалах. Если коэффициенты уравнения целочисленны, то можно попытаться подобрать рациональный корень и понизить степень уравнения. В частности, целые корни, если они есть, являются делителями свободного члена.

Законы элементарной алгебры[]

Вычисление значения выражения

Порядок выполнения операций указывается скобками. Если скобок нет, то приоритетность, в порядке убывания, следующая.

1. Возведение в степень.
2. Вычисление функции.
3. Умножение и деление.
4. Сложение и вычитание.

Примеры:

• abc=a(bc){\displaystyle a^{b^{c}}=a^{(b^{c})}}
• sin⁡x2=sin⁡(x2){\displaystyle \sin x^{2}=\sin(x^{2})}
• sin⁡a+b=(sin⁡a)+b{\displaystyle \sin a+b=(\sin a)+b}

При вычислении значения выражения вместо буквенных символов подставляют их числовые значения, соответствующие конкретной задаче. Множество числовых значений, при которых выражение имеет смысл, называется областью допустимых значений этого выраженияШаблон:Sfn. Пример: для выражения  a+ba−b{\displaystyle ~{\frac {a+b}{a-b}}} область допустимых значений — все пары a,b{\displaystyle a,b}, в которых a≠b{\displaystyle a\neq b}.

Свойства операций

Коммутативность (перестановочное свойство) сложения:

a+b=b+a. {\displaystyle a+b=b+a.\ }

• Вычитание есть действие, обратное сложению.
• Вычитание числа b равносильно сложению с числом, противоположным b:

a−b=a+(−b). {\displaystyle a-b=a+(-b).\ }

Коммутативность (перестановочное свойство) умножения:

a⋅b=b⋅a {\displaystyle a\cdot b=b\cdot a\ }

• Деление есть действие, обратное умножению.
• Деление на нуль невозможно.
• Деление на число b равносильно умножению на число, обратное к b:

ab=a(1b).{\displaystyle {a \over b}=a\left({1 \over b}\right).}

• Возведение в степень не коммутативно. Поэтому у него имеются две обратные операции: извлечение корня и логарифмирование

  Пример: если 3x=10{\displaystyle 3^{x}=10}, то x=log3⁡10.{\displaystyle x=\log _{3}10.} Если x2=10{\displaystyle x^{2}=10}, то  x=10.{\displaystyle ~x={\sqrt {10}}.}

  .

• Корень чётной степени из отрицательного числа не существует (среди вещественных чисел). См. комплексные числа.
• Ассоциативное (сочетательное) свойство сложения: (a+b)+c=a+(b+c).{\displaystyle (a+b)+c=a+(b+c).}
• Ассоциативное (сочетательное) свойство умножения: (ab)c=a(bc).{\displaystyle (ab)c=a(bc).}
• Дистрибутивное (распределительное) свойство для умножения: c(a+b)=ca+cb.{\displaystyle c(a+b)=ca+cb.}
• Дистрибутивное (распределительное) свойство для возведения в степень: (ab)c=acbc.{\displaystyle (ab)^{c}=a^{c}b^{c}.}
• Сложение показателей степени: abac=ab+c.{\displaystyle a^{b}a^{c}=a^{b+c}.}
• Умножение показателей степени: (ab)c=abc.{\displaystyle (a^{b})^{c}=a^{bc}.}

Свойства равенства

• Если a=b{\displaystyle a=b} и b=c{\displaystyle b=c}, то a=c{\displaystyle a=c} (транзитивность равенства).
• a=a{\displaystyle a=a} (рефлексивность).
• Если a=b{\displaystyle a=b}, то b=a{\displaystyle b=a} (симметричность).

Другие законы

• Если a=b{\displaystyle a=b} и c=d{\displaystyle c=d}, то a+c=b+d.{\displaystyle a+c=b+d.} (аддитивность

  Если a=b{\displaystyle a=b}, то a+c=b+c{\displaystyle a+c=b+c} для любого c

  равенства)

• Если a=b{\displaystyle a=b} и c=d{\displaystyle c=d}, то ac{\displaystyle ac} = bd.{\displaystyle bd.} (мультипликативность

  Если a=b{\displaystyle a=b}, то ac=bc{\displaystyle ac=bc} для любого c

  равенства)

• Если значения двух символов совпадают, то вместо одного можно подставить другой (принцип подстановки).
• Если a>b{\displaystyle a>b} и b>c{\displaystyle b>c}, то a>c{\displaystyle a>c} (транзитивность порядка).
• Если a>b{\displaystyle a>b}, то a+c>b+c{\displaystyle a+c>b+c} для любого c.
• Если a>b{\displaystyle a>b} и c>{\displaystyle c>0}, то ac>bc.{\displaystyle ac>bc.}
• Если a>b{\displaystyle a>b} и c<{\displaystyle c<0}, то ac<bc.{\displaystyle ac<bc.}

Некоторые алгебраические тождества

Шаблон:Seealso

(a+b)(a−b)=a2−b2{\displaystyle (a+b)(a-b)=a^{2}-b^{2}}

(a+b)2=a2+2ab+b2;(a−b)2=a2−2ab+b2{\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2};\;(a-b)^{2}=a^{2}-2ab+b^{2}}

(a+b)3=a3+3a2b+3ab2+b3;(a−b)3=a3−3a2b+3ab2−b3{\displaystyle (a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3};\;(a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}}

a3+b3=(a+b)(a2−ab+b2);a3−b3=(a−b)(a2+ab+b2){\displaystyle a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2});\;a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})}

9 класс

№ урока	Тема
1	Повторение материала 8 класса 11 минут 54секунд
2	Повторение материала 8 класса. Решение систем уравнений 13 минут 57секунд
3	Квадратичная функция.y = ax2 12 минут 11секунд
4	Квадратичная функция y = ax2 + bx + c 14 минут 13секунд
5	Графиком квадратичной функции y = ax2 + bx + c. 14 минут 10секунд
6	Область определения функции 14 минут 11секунд
7	Промежутки возрастания и убывания функции 13 минут 51секунд
8	Чётность и нечётность функции 9 минут 51секунд
9	Неравенства и уравнения содержащие степень 14 минут 43секунд
10	Решение задач 12 минут 56секунд
11	Решение задач 11 минут 36секунд
12	Решение систем уравнений второго порядка. 14 минут 21секунд
13	Решение простейших систем, содержащих вторую степень 11 минут 37секунд
14	Решение простейших систем, содержащих вторую степень. 11 минут 37секунд
15	Различные способы решения систем уравнений. 11 минут 11секунд
16	Решение задач (1). 13 минут 5секунд
17	Решение задач.Закрепление (1). 11 минут 36секунд
18	Решение неравенств и систем неравенств второй степени с одной переменной. 9 минут 35секунд
19	Решение примеров. 17 минут 35секунд
20	Решение практических задач. 19 минут 35секунд
21	Решение квадратных неравенств методом интервалов 17 минут 5секунд
22	Решение примеров 15 минут 11секунд
23	Доказательство простых неравенств 14 минут 4секунд
24	Решение примеров 12 минут 17секунд
25	Решение примеров 11 минут 49секунд
26	Решение практических задач. 8 минут 11секунд
27	Решение практических задач. 9 минут 24секунд
28	Радианная мера угла 10 минут 32секунд
29	Поворот точки вокруг начала координат 14 минут 42секунд
30	Определение синуса. Косинуса. Тангенса и Котангенса угла 14 минут 6секунд
31	Решение примеров 13 минут 15секунд
32	Решение примеров 12 минут 38секунд
33	Зависимость между синусом, косинусом и тангенсом одного и того же аргумента 9 минут 39секунд
34	Решение примеров 12 минут 13секунд
35	Тригонометрические тождества 15 минут 18секунд
36	Радианная мера угла 10 минут 36секунд
37	Синус, косинус, тангенс и котангенс углов а И -а 12 минут 54секунд
38	Формулы сложения 11 минут 22секунд
39	Решение примеров 16 минут 16секунд
40	Синус и косинус двойного угла 16 минут 24секунд
41	Формулы приведения 10 минут 12секунд
42	Сумма и разность синусов. Сумма и разность косинусов 17 минут 20секунд
43	Синус, косинус, тангенс и котангенс углов а и -а 12 минут 44секунд
44	Числовые последовательности 17 минут 0секунд
45	Арифметические прогрессия 11 минут 4секунд
46	Сумма n первых членов арифметической прогрессии 11 минут 53секунд
47	Геометрическая прогрессия 10 минут 45секунд
48	Бесконечно убывающая геометрическая прогрессия 19 минут 29секунд
49	Решение задач 19 минут 29секунд
50	Бесконечно убывающая геометрическая прогрессия 10 минут 17секунд
51	Решение задач 9 минут 35секунд
52	Практические и мепредметные задачи (2 часть) 8 минут 26секунд
53	Решение задач (1 часть) 10 минут 1секунд
54	Решение задач (2 часть) 10 минут 1секунд
55	События 16 минут 3секунд
56	Решение задач 6 минут 30секунд
57	Вероятность события 9 минут 9секунд
58	Решение задач 8 минут 56секунд
59	Относительная частота случайного события 11 минут 40секунд
60	Случайные величины (1) 8 минут 5секунд
61	Случайные величины (2 часть) 8 минут 5секунд
62	Числовые характеристики случайных величин 10 минут 39секунд
63	Решение задач 9 минут 4секунд
64	Повторение 9 минут 58секунд

10 класс

№ урока	Тема
1	Множества. Операции над множествами 11 минут 16секунд
2	Множества. Решение задач 16 минут 20секунд
3	Решение задач на множества. 12 минут 52секунд
4	Высказывание отрицание конъюнкция и дизъюнкция 10 минут 26секунд
5	Логическая равносильность. Законы логики 11 минут 43секунд
6	Импликация, конверсия, инверсия и контрапозиция 11 минут 3секунд
7	Предикаты и кванторы 9 минут 57секунд
8	Законы правильного мышления (аргументации). Софизмы и парадоксы 11 минут 20секунд
9	Законы правильного мышления 11 минут 20секунд
10	Простой и сложный процент 15 минут 21секунд
11	Решение задач на простой и сложный процент 10 минут 44секунд
12	Система рациональных уравнений 18 минут 22секунд
13	Иррациональные уравнения и их системы 13 минут 35секунд
14	Простые рациональные уравнения и их системы 13 минут 16секунд
15	Простые иррациональные уравнения 16 минут 19секунд
16	Простые иррациональные уравнения и их системы 15 минут 58секунд
17	Простые иррациональные уравнения (2) 15 минут 33секунд
18	Задания контрольной работы 13 минут 5секунд
19	Решение задач 7 минут 44секунд
20	Решение задач. Повторение 12 минут 2секунд
21	Система простых иррациональных уравнений 13 минут 20секунд
22	Показательные уравнения 16 минут 4секунд
23	Показательные уравнения 12 минут 51секунд
24	Простые показательные уравнения и их системы 10 минут 26секунд
25	Простые показательные уравнения и их системы 13 минут 51секунд
26	Приближенное решение уравнений 16 минут 52секунд
27	Приближенное решение уравнений (2) 14 минут 9секунд
28	Простые рациональные неравенства 13 минут 1секунд
29	Простые рациональные неравенства и их системы 13 минут 10секунд
30	Простые иррациональные неравенства (1-часть) 9 минут 0секунд
31	Простые иррациональные неравенства (2-часть) 10 минут 13секунд
32	Отношения и отображения 11 минут 46секунд
33	Знаки синуса, косинуса и тангеса 16 минут 45секунд
34	Решение задач 16 минут 47секунд
35	Решение примеров 19 минут 29секунд
36	Понятие монотонности. Наименьшего и наибольшего значении элементарных функции 9 минут 14секунд
37	Линейные и квадратичные функции 9 минут 28секунд
38	Решение примеров 11 минут 13секунд
39	Простые рациональные уравнения и их системы 13 минут 20секунд
40	Функции y=sinx, y=cosx и моделирование с их помощью 10 минут 10секунд
41	Периодические процессы и наблюдения за ними 13 минут 10секунд
42	Периодические процессы и наблюдения за ними 12 минут 32секунд
43	Периодические процессы и наблюдения за ними 20 минут 5секунд
44	Простейшие тригонометрические уравнения 13 минут 13секунд
45	Простейшие тригонометрические уравнения 17 минут 33секунд
46	Простейшие тригонометрические неравенства 16 минут 26секунд
47	Преобразования графиков 12 минут 16секунд
48	Графики простых функций. Заданных в параметрическом виде 17 минут 55секунд
49	Показательная функция и её график 11 минут 19секунд
50	Простейшие тригонометрические уравнения (2-часть) 17 минут 33секунд
51	Решение задач 17 минут 12секунд
52	Простейшие логарифмические уравнения 11 минут 25секунд
53	Решение примеров 13 минут 55секунд
54	Простейшие логарифмические неравенства 12 минут 2секунд
55	Моделирование с помощью показательной и логарифмической функции (1 часть) 11 минут 5секунд
56	Моделирование с помощью показательной и логарифмической функции 9 минут 28секунд
57	Моделирование с помощью показательной и логарифмической функции (3) 10 минут 54секунд
58	Комплексные числа и операции над ними 12 минут 7секунд
59	Изображение комплексного числа 11 минут 0секунд
60	Комплексные числа вида 13 минут 29секунд
61	Произведение и частное комплексных чисел, заданных в тригонометрической форме 16 минут 4секунд
62	Извлечение квадратного корня из числа 8 минут 34секунд
63	Решение примеров 7 минут 53секунд

Конспекты по предмету «Алгебра»

Изучение Алгебры шаг за шагом. Онлайн-учебник.

Кодификатор ОГЭ  ТЕСТЫ по АЛГЕБРЕ  Справочник для ОГЭ

Математика 5 и 6 классов

Дорофеев 5 класс. Контрольные работы

Учебник Алгебра 7 Мордкович

Учебник Алгебра 8 Макарычев Алгебра 8 класс. Поурочные планы

Материалы для УМК Мерзляк

Электронные формы учебников для 6-9 классов (ссылки):

• Онлайн-учебник: Математика 6 кл. / Мерзляк, Полонский, Якир (2014)
• Онлайн-учебник: Алгeбра 7 (углубленное изучение). Мерзляк, Поляков (2019)
• Онлайн-учебник: Алгeбра. 7 класс. В 2 частях/Мордкович М.: Мнемозина (2019)
• Онлайн-учебник: Алгeбра. 7 кл. / Макарычев и др. М.: Просвещение (2018)
• Онлайн-учебник: Алгeбра 8 (углубленное изучение). Мерзляк, Поляков (2019)
• Онлайн-учебник: Алгебра 8 Мордкович, Семенов (Просвещение, 2018)
• Онлайн-учебник: Алгебра 8 кл. Макарычев и др. (Просвещение 2019)
• Онлайн-учебник: Алгeбра 9 класс. Макарычев (Просвещение, 2017)
• Онлайн-учебник: Алгeбра 9 класс. Мордкович (Мнемозина, 2019)

Готовая домашняя работа, ГДЗ для 6-9 классов (ссылки)

• Решебник: ГДЗ Математика 5 класс Мерзляк Учебник
• Решебник: ГДЗ Математика 6 Мерзляк Учебник
• Решебник: ГДЗ Математика 6 Виленкин. Учебник в 2 частях.
• Решебник: ГДЗ Алгебра 7 класс. Учебник Макарычев, 2018.
• Решебник:  ГДЗ Алгебра 8 Макарычев Учебник (упр. 1-262)

Алгебра (от араб. الْجَبْر‎, «аль-джабр» — восполнение) — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики. Слово «алгебpа» также употребляется в общей алгебре в названиях различных алгебраических систем. В более широком смысле под алгеброй понимают раздел математики, посвящённый изучению операций над элементами множества произвольной природы, обобщающий обычные операции сложения и умножения чисел.

Алгeбра как раздел математики традиционно включает следующие категории: Элементарная, Общая, Универсальная, Линейная (включая матрицы) и Алгебраическая комбинаторика.

Элементарная алгебpа, которая изучает свойства операций с вещественными числами. В ней постоянные и переменные обозначаются буквенными символами. Элементарная алгeбpа содержит правила преобразования математических выражений и уравнений с использованием этих символов. Обычно преподаётся в школе под названием aлгебра.

Кодификатор ОГЭ  ТЕСТЫ по АЛГЕБРЕ  Справочник для ОГЭ

Источники идей и цитат для конспектов по Алгебре:

1. Макарычев Ю.Н. Учебники по Алгебре для 7, 8, 9 классов. — М.: Мнемозина.
2. Лахова Н.В. Алгебра за 7 занятий. 7 класс: учебное пособие — М.: Просвещение, 2016.
3. Томилина М.Е. Справочник по математике. 5-9 классы — СПб.: Издательский дом «Литера».
4. ОГЭ. Математика : универсальный справочник / И.В. Третьяк. — М.: Эксмо, 2016
5. Мерзляк А.Г. Учебники по Алгебре для 7, 8, 9 классов. — М.: Вентана-Граф.
6. ОГЭ. Математика. Справочник с комментариями ведущих экспертов / Л.В. Кузнецова — М.: Просвещение.

(с) Цитаты из вышеуказанных учебных пособий использованы на сайте в незначительных объемах, исключительно в учебных и информационных целях (пп. 1 п. 1 ст. 1274 ГК РФ). 

↑яБЪГЭ ЮКЦЕАПШ Я ДПСЦХЛХ НАКЮЯРЪЛХ ЛЮРЕЛЮРХЙХ

пЪД ПЮГДЕКНБ ЛЮРЕЛЮРХЙХ БНГМХЙ МЮ ЦПЮМХЖЕ ЮКЦЕАПШ Я ДПСЦХЛХ ВЮЯРЪЛХ ЛЮРЕЛЮРХЙХ Х НЯМНБЮМ МЮ ПЮЯЯЛНРПЕМХХ ДНОНКМХРЕКЭМШУ ЯРПСЙРСП, ЯНЦКЮЯНБЮММШУ Я ЮКЦЕАПЮХВЕЯЙХЛХ НОЕПЮЖХЪЛХ.

рНОНКНЦХВЕЯЙЮЪ ЮКЦЕАПЮ МЮВЮКЮ ЯБНЕ ЯСЫЕЯРБНБЮМХЕ Я ЙНМЙПЕРМШУ РНОНКНЦХВЕЯЙХУ ОНКЕИ (БЕЫЕЯРБЕММШУ, ЙНЛОКЕЙЯМШУ, p-ЮДХВЕЯЙХУ ВХЯЕК) Х ЦПСОО кХ. б ДЮКЭМЕИЬЕЛ, АШКХ ПЮГБХРШ РЕНПХЪ РНОНКНЦХВЕЯЙХУ ОНКЕИ Х РЕК, РЕНПХЪ ЦПСОО кХ Х НАЫХУ РНОНКНЦХВЕЯЙХУ ЦПСОО, РЕНПХЪ РНОНКНЦХВЕЯЙХУ ЙНКЕЖ (Б РНЛ ВХЯКЕ МНПЛХПНБЮММШЕ ЙНКЭЖЮ (АЮМЮУНБШ ЮКЦЕАПШ)), РЕНПХЪ РНОНКНЦХВЕЯЙХУ ОНКСЦПСОО, РЕНПХЪ РНОНКНЦХВЕЯЙХУ КХМЕИМШУ ОПНЯРПЮМЯРБ Х РНОНКНЦХВЕЯЙХУ ЛНДСКЕИ.

рЕНПХЪ СОНПЪДНВЕММШУ ЮКЦЕАПЮХВЕЯЙХУ ЯХЯРЕЛ БЙКЧВЮЕР Б ЯЕАЪ ПЮГБХРСЧ РЕНПХЧ СОНПЪДНВЕММШУ ЦПСОО, РЕНПХЧ СОНПЪДНВЕММШУ ОНКЕИ, РЕК Х ЙНКЕЖ, РЕНПХЧ СОНПЪДНВЕММШУ ОНКСЦПСОО, ЮКЦЕАПЮХВЕЯЙХЕ ЮЯОЕЙРШ СОНПЪДНВЕММШУ ЛМНФЕЯРБ.

дХТТЕПЕМЖХЮКЭМЮЪ ЮКЦЕАПЮ – ПЮГДЕК ЮКЦЕАПШ, ХГСВЮЧЫХИ НАЗЕЙРШ, Б ЙНРНПШУ, МЮПЪДС Я НЯМНБМШЛХ НОЕПЮЖХЪЛХ, ХЛЕЧРЯЪ НОЕПЮРНПШ ДХТТЕПЕМЖХПНБЮМХЪ: ДХТТЕПЕМЖХЮКЭМШЕ ОНКЪ Х ЙНКЭЖЮ, ДХТТЕПЕМЖХЮКЭМШЕ ЛНДСКХ, ДХТТЕПЕМЖХЮКЭМШЕ ЮКЦЕАПЮХВЕЯЙХЕ ЛМНЦННАПЮГХЪ. пЮГБХРШЛХ МЮОПЮБКЕМХЪЛХ ДХТТЕПЕМЖХЮКЭМНИ ЮКЦЕАПШ ЪБКЪЧРЯЪ РЕНПХЪ цЮКСЮ ДХТТЕПЕМЖХЮКЭМШУ ОНКЕИ, РЕНПХЪ ДХТТЕПЕМЖХЮКЭМШУ ЮКЦЕАПЮХВЕЯЙХУ ЦПСОО, ЮКЦЕАПЮХВЕЯЙХУ ДХТТЕПЕМЖХЮКЭМШУ СПЮБМЕМХИ, РЕНПХЪ ДХТТЕПЕМЖХЮКЭМШУ ПЮГЛЕПМНЯРМШУ ЛМНЦНВКЕМНБ, ЙНЛОЭЧРЕПМЮЪ ДХТТЕПЕМЖХЮКЭМЮЪ ЮКЦЕАПЮ. дХТТЕПЕМЖХЮКЭМЮЪ ЮКЦЕАПЮ ПЮГБХБЮЕР ЮКЦЕАПЮХВЕЯЙХИ ЮООЮПЮР ДКЪ РЕНПХХ ДХТТЕПЕМЖХЮКЭМШУ СПЮБМЕМХИ, Б РН БПЕЛЪ ЙЮЙ ПЮГМНЯРМЮЪ ЮКЦЕАПЮ ПЮГБХБЮЕР ЮКЦЕАПЮХВЕЯЙСЧ РЕУМХЙС ДКЪ ПЮГМНЯРМШУ СПЮБМЕМХИ.

я 40-У ЦНДНБ Б ЛЮРЕЛЮРХЙС БНЬКН ОНМЪРХЕ ЙЮРЕЦНПХХ, БШДЕКЪЧЫЕЕ ПЪД ЮКЦЕАПЮХВЕЯЙХУ ЯБНИЯРБ ЯНБНЙСОМНЯРЕИ ЛНПТХГЛНБ НДМНРХОМШУ ЛЮРЕЛЮРХВЕЯЙХУ НАЗЕЙРНБ (ЛМНФЕЯРБ, РНОНКНЦХВЕЯЙХУ ОПНЯРПЮМЯРБ, ЦПСОО, ЛНДСКЕИ Х Р.О.). бНГМХЙЬХИ БМЮВЮКЕ ОНД БКХЪМХЕЛ ЮКЦЕАПЮХВЕЯЙНИ РНОНКНЦХХ, Б ДЮКЭМЕИЬЕЛ ЪГШЙ ЙЮРЕЦНПХИ Х ТСМЙРНПНБ ЯРЮК ХЦПЮРЭ НАЗЕДХМЪЧЫСЧ Х СМХТХЖХПСЧЫСЧ ПНКЭ ДКЪ ЛМНЦХУ ПЮГДЕКНБ ЛЮРЕЛЮРХЙХ (Б ВЮЯРМНЯРХ, ДКЪ ЮМЮКХГЮ БЕГДЕЯСЫЕЦН ОПХМЖХОЮ ДБНИЯРБЕММНЯРХ). нДМХЛ ХГ МЮХАНКЕЕ ПЮГБХРШУ ПЮГДЕКНБ РЕНПХХ ЙЮРЕЦНПХИ ЪБКЪЕРЯЪ РЕНПХЪ ЮАЕКЕБШУ ЙЮРЕЦНПХИ, Б ПЮЛЙЮУ ЙНРНПНИ НЯСЫЕЯРБКЪЧРЯЪ НЯМНБМШЕ ОНЯРПНЕМХЪ ЦНЛНКНЦХВЕЯЙНИ ЮКЦЕАПШ. юЙРХБМН ПЮГБХБЮЕРЯЪ РЕНПХЪ РНОНЯНБ.

цНЛНКНЦХВЕЯЙЮЪ ЮКЦЕАПЮ БНГМХЙКЮ ЙЮЙ ПЮГДЕК ЮКЦЕАПШ, НЯМНБМШЛ НАЗЕЙРНЛ ХГСВЕМХЪ ЙНРНПНЦН ЪБКЪЧРЯЪ ОПНХГБНДМШЕ ТСМЙРНПШ МЮ ПЮГКХВМШУ ЙЮРЕЦНПХЪУ ЮКЦЕАПЮХВЕЯЙХУ НАЗЕЙРНБ (ЛНДСКЕИ МЮД ДЮММШЛ ЙНКЭЖНЛ, ОСВЙНБ Х Р.Д.). нДМХЛ ХГ ХЯРНЙНБ ЦНЛНКНЦХВЕЯЙНИ ЮКЦЕАПШ ЪБХКЮЯЭ РЕНПХЪ ЦНЛНКНЦХИ РНОНКНЦХВЕЯЙХУ ОПНЯРПЮМЯРБ. б ЯБНЧ НВЕПЕДЭ, Б ЮКЦЕАПЕ Б ЯБЪГХ Я ХГСВЕМХЕЛ ПЮЯЬХПЕМХИ ЦПСОО ТЮЙРХВЕЯЙХ ПЮЯЯЛЮРПХБЮКХЯЭ ОЕПБЮЪ Х БРНПЮЪ ЦПСООШ ЦНЛНКНЦХИ Х ЙНЦНЛНКНЦХИ. цПСООШ ЙНЦНЛНКНЦХИ ЦПСОО БН БЯЕУ ПЮГЛЕПМНЯРЪУ АШКХ ББЕДЕМШ я.щИКЕМАЕПЦНЛ Х я.лЮЙКЕИМНЛ (1943 Ц.), д.й.тЮДДЕЕБШЛ (1947 Ц.). гМЮВХРЕКЭМШИ ОНДЦНРНБХРЕКЭМШИ ЛЮРЕПХЮК АШК ПЮГПЮАНРЮМ Б РЕНПХХ ЮЯЯНЖХЮРХБМШУ ЮКЦЕАП, ЮКЦЕАП кХ, Б РЕНПХХ ЙБЮДПЮРХВМШУ ТНПЛ. б ЯЕПЕДХМЕ 40-У ЦНДНБ 20 Б. ЦНЛНКНЦХВЕЯЙЮЪ ЮКЦЕАПЮ БШДЕКЪЕРЯЪ Б ЯЮЛНЯРНЪРЕКЭМСЧ НАКЮЯРЭ ЮКЦЕАПШ Я ПЮГБХРНИ РЕНПХЕИ ОПНХГБНДМШУ ТСМЙРНПНБ, ПЕГНКЭБЕМР, ЯОЕЙРПЮКЭМШУ ОНЯКЕДНБЮРЕКЭМНЯРЕИ, ЦНЛНКНЦХВЕЯЙХУ СЛМНФЕМХИ, ЦНЛНКНЦХИ Х ЙНЦНЛНКНЦХИ ЮКЦЕАП. лНЦНЦПЮТХЪ ю.йЮПРЮМЮ Х я.щИКЕМАЕПЦЮ ДНЯРЮРНВМН ОНКМН ОПЕДЯРЮБХКЮ НЯМНБШ ЦНЛНКНЦХВЕЯЙНИ ЮКЦЕАПШ. лЕРНДШ ЦНЛНКНЦХВЕЯЙНИ ЮКЦЕАПШ ЬХПНЙН ХЯОНКЭГСЧРЯЪ Б ЯЮЛШУ ПЮГКХВМШУ ПЮГДЕКЮУ ЛЮРЕЛЮРХЙХ – Б ТСМЙЖХНМЮКЭМНЛ ЮМЮКХГЕ, Б РЕНПХХ ТСМЙЖХИ ЙНЛОКЕЙЯМНЦН ОЕПЕЛЕММНЦН, Б РЕНПХХ ДХТТЕПЕМЖХЮКЭМШУ СПЮБМЕМХИ, Б K-РЕНПХХ, Б ЮКЦЕАПЮХВЕЯЙНИ ЦЕНЛЕРПХХ, Б ЮКЦЕАПЮХВЕЯЙНИ РЕНПХХ ВХЯЕК.

Новые технологии науки алгебра

В настоящее время существует множество новых технологий, связанных с наукой алгебра, которые позволяют более эффективно применять ее на практике.

Ниже приведен список некоторых из них:

1. Компьютерные программы для решения уравнений и систем уравнений — это программы, которые могут автоматически решать сложные математические задачи, которые ранее могли занять много времени и усилий.
2. Математические моделирование — это процесс создания моделей реальных систем, используя алгебру и другие математические инструменты. Математические моделирование широко используется в науке, инженерии, физике, экономике и других областях.
3. Машинное обучение — это метод искусственного интеллекта, который использует алгебру для создания моделей, которые могут самостоятельно обучаться и принимать решения на основе большого объема данных.
4. Квантовые вычисления — это технология, основанная на принципах квантовой механики, которая позволяет выполнять сложные вычисления, недоступные для традиционных компьютеров. Алгебра играет важную роль в квантовых вычислениях, поскольку она используется для представления квантовых состояний и операций.
5. Интерактивное обучение — это метод обучения, который использует интерактивные технологии, такие как игры и симуляции, для помощи студентам в изучении математики и алгебры. Интерактивные технологии позволяют студентам изучать материал в своем собственном темпе и обеспечивают более эффективный способ обучения.

Эти новые технологии помогают сделать науку алгебра более доступной и применимой в различных областях науки и технологии.

Преобразование (конструирование) графиков функций

• График функции y=- f(x) получается из графика функции y=f (x) зеркальным отражением от оси абсцисс.
• График функции y=|f(x)| получается зеркальным отражением от оси абсцисс той части графика функции y=f (x), которая лежит ниже оси абсцисс.
• График функции y=f(|x|) получается из графика функции y=f (x) следующим образом: оставляют часть графика справа от оси ординат и отображают эту же часть симметрично ей самой относительно оси ординат.
• График функции y=A∙f(x) получается из графика функции y=f (x) растяжением в А раз вдоль оси ординат. (Ордината каждой точки графика функции y=f (x) умножается на число А).
•  График функции y=f(k∙x) получается из графика функции y=f (x) сжатием в k раз при k > 1 или растяжением в k раз при 0
•  График функции y=f(x- m) получается из графика функции y=f (x) параллельным переносом на m единичных отрезков вдоль оси абсцисс.
•  График функции y=f(x)+n получается из графика функции y=f (x) параллельным переносом на n единичных отрезков вдоль оси ординат.

Врата алгебры

1.1. Множества1.1.1. Подмножества1.1.2. Числовые множества1.1.3. Мощность множества1.1.4. Операции (действия) с множествами1.1.5. Отображение множеств1.1.6. Обратное отображение1.1.7. Композиция отображений

1.2. Основы математической логики1.2.1. Высказывания и высказывательные формы1.2.2.Логические операции (действия над высказываниями)1.2.3. Отрицание высказывания1.2.4. Конъюнкция (логическое умножение высказываний)1.2.5. Дизъюнкция (логическое сложение высказываний)1.2.6. Импликация. Необходимое условие. Достаточное условие1.2.7. Логическое следствие1.2.8. Эквиваленция. Необходимое и достаточное условие