Как найти радиус окружности вписанной в правильный угольник

Нахождение радиуса вписанной окружности

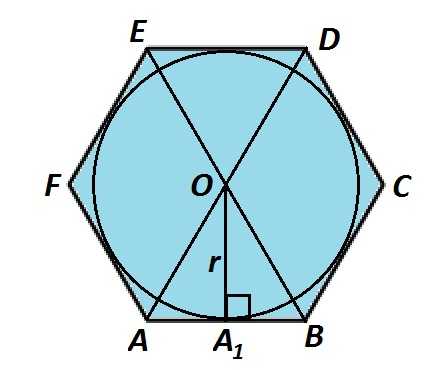
В шестиугольник АВСDEF вписана окружность. Ее центр находится на пересечении диагоналей в точке О. Если известна сторона данного шестиугольника, то можно найти радиус вписанной окружности, рассмотрев прямоугольный треугольник \(А_1ОВ\). Гипотенуза \(ΔА_1ОВ\) равна стороне шестиугольника, ОВ=АВ. Перпендикуляр \(ОА_1\) делит сторону АВ пополам, то есть \(А_1В=\frac12·АВ=\frac12·ОВ\). Так как \(ОВ^2=ОА_1^2+А_1В^2\), то \(ОА_1=\sqrt{ОB^2-A_1В^2}=\sqrt{ОB^2-A_1В^2}=\sqrt{0B^2-\left(\frac12\cdot0B\right)^2}=\frac{\sqrt3}2OB\). Получаем следующую формулу:

Формула 1

\(r=\frac{\sqrt3}2·a\)

где r — радиус окружности, вписанной в правильный шестиугольник,

а — сторона правильного шестиугольника.

Основные формулы

Для каждого треугольника существует набор формул, с помощью которых можно определить его элементы. Чаще всего приходится выяснять длины сторон, площадь, высоты и периметр. При этом если известны боковые грани, можно найти практически любые остальные параметры.

Вокруг правильной фигуры можно описать круг, причём окружность можно и вписать в середину. Что интересно, их центры совпадут между собой и с местом пересечения высот. В этом случае радиус внешнего круга равняется R = (a * √‎3) / 3 = a / 2 * sin (a), а внутреннего: r = (a * √‎3) / 6 = R / 2. Чтобы найти высоту, зная радиус, используют выражение: h = (3 *R) / 2. Кроме этой формулы, довольно часто применяют равенство, связывающее сторону и перпендикуляр: h = (a * √‎3) / 2.

Доказательство верности формулы для нахождения радиуса вписанной окружности можно построить исходя из выражения, справедливого к равнобедренной фигуре: r = b / 2 √(‎(2 a — b) / (2 a + b)). Так как стороны равны, то a = b. Получается, что r = a / 2 √‎(2a — a) / (2a + a) = (a / 2) * √‎(1 / 3) = a / (2 * √‎3) = (a √‎3) / 6.

Чтобы определить длину стороны, нужно знать высоту и теорему Пифагора. Согласно ей, квадрат гипотенузы находится как сумма квадратов высоты и длины разделённого основания. Применяя теорему к правильной фигуре, можно записать: AB2 = h2 + (AB / 2)2. Это равенство решают следующим образом: AB2 = h2 + AB2 / 22. Выражение можно преобразовать в вид: (3a2 / 4) = h 2 → a 2 = (4 * h2) / 3 → a 2 = √‎((4 * h2) / 3) → a = (2 * h) / √3.

Из других существующих формул можно перечислить те, что чаще всего применяют при решении примеров:

• Площадь. Находят из выражения: S = (a 2 * √3) / 4. Вывести эту формулу довольно просто. Если взять за основу, что равенство для площади верно, то исходя из свойств фигуры можно записать: S = ½ * a2 * sin 60 = ½ * a2 * √3 / 2 = (√3 / 4) * a2. Что и следовало доказать.
• Периметр. Чтобы его определить, нужно сложить длины всех сторон, но так как в правильной фигуре они равны, можно воспользоваться формулой: P = 3 * a.

Существуют ещё 2 значимые теоремы: косинусов и синусов. Согласно первой, квадрат стороны фигуры будет ранятся удвоенному произведению двух оставшихся отрезков и косинусу угла между ними, отнятому из суммы квадратов: a2 = b2 + c2 — 2 * b * c * cos (a). Согласно же второй, длины отрезков пропорциональны синусам углов, лежащих напротив: a / sin (a) = b / sin (b) = c / sinс.

Радиус вписанной окружности в правильный многоугольник, формула

Правильный многоугольник — это многоугольник с равными сторонами и углами. Угол между двумя соседними вершинами правильного n-угольника равен:

Построим треугольник AOB отдельно. Об этом треугольнике мы знаем: он равнобедренный, и высота этого треугольника это радиус вписанной окружности правильного многоугольника. Также нам известна длина основания a этого треугольника — которое является стороной исходного правильного многоугольника.

Также известен угол между бедрами — по формуле (1). Опустим высоту на основание и рассмотрим получившийся прямоугольный треугольник. При помощи тригонометрических функций острого угла получим:

отсюда получим формулу радиуса вписанной окружности правильного многоугольника:

(a — сторонa правильного многоугольника; n — число сторон правильного многоугольника; r — радиус вписанной окружности правильного многоугольника)

Примеры применения формулы в задачах

Пример 1: Дан восьмиугольник с вписанной окружностью радиусом 5 см. Найдите длину одной стороны восьмиугольника.

Решение:

Так как окружность вписана в восьмиугольник, то радиус окружности является расстоянием от центра восьмиугольника до середины стороны. Так как восьмиугольник имеет восемь равных сторон, то мы можем разделить его на восемь равных треугольников, где каждый треугольник имеет площадь: S_тр = (p/2) * r, где p — периметр треугольника, r — радиус вписанной окружности. Тогда для всего восьмиугольника длина одной стороны будет равна: a = 2 * r * Sin(π/8) = 2 * 5 * Sin(π/8) ≈ 6,14 см.

Пример 2: В треугольнике ABC вписана окружность радиуса 4 см. Найдите значение угла А при условии, что AC = 10 см и BC = 8 см.

Решение:

Обозначим за x значение угла А. Так как окружность вписана в треугольник, то высота треугольника, проведенная к стороне АС, является радиусом вписанной окружности. Тогда, зная, что высота равна (b*c*Sin(x))/2, где b и c — соответствующие стороны треугольника, можем составить уравнение: 4 = (8*10*Sin(x))/20. Отсюда получим Sin(x) = 1/5. Так как угол А меньше π/2, то он будет острым, а значит Sin(x) = BC/AC. Из этого следует, что угол А = 53,13 градусов.

Пример 3: Дан пятиугольник, вписанный в окружность радиуса 7 м. Найдите площадь пятиугольника, если одна из его сторон равна 8 м.

Решение:

Так как пятиугольник вписан в окружность, то мы можем разделить его на пять равных треугольников, где каждый треугольник имеет площадь: S_тр = (p/2) * r, где p — периметр треугольника, r — радиус вписанной окружности. Так как одна из сторон пятиугольника равна 8 м, то периметр одного треугольника будет равен 5 * 8 = 40 м. Тогда площадь одного треугольника будет равна: S_тр = (40/2) * 7 = 140 м2. Так как пятиугольник состоит из пяти таких треугольников, то его площадь будет равна: 700 м2.

Все формулы для радиуса вписанной окружности

Радиус вписанной окружности в треугольник

a, b, c — стороны треугольника

p — полупериметр, p=(a+b+c)/2

Формула радиуса вписанной окружности в треугольник (r):

Радиус вписанной окружности в равносторонний треугольник

a — сторона треугольника

r — радиус вписанной окружности

Формула для радиуса вписанной окружности в равносторонний треугольник (r):

Радиус вписанной окружности равнобедренный треугольник

1.

Формулы радиуса вписанной окружности если известны: стороны и угол

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

α — угол при основании

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :

2. Формулы радиуса вписанной окружности если известны: сторона и высота

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

h — высота

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :

a, b — катеты треугольника

с — гипотенуза

Формула радиуса вписанной окружности в прямоугольный треугольник (r):

Радиус вписанной окружности в равнобочную трапецию

с — нижнее основание

b — верхнее основание

a — боковые стороны

h — высота

Формула радиуса вписанной окружности равнобочной трапеции (r):

a — сторона квадрата

Формула радиуса вписанной окружности в квадрат (r):

Радиус вписанной окружности в ромб

1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол

a — сторона ромба

D — большая диагональ

d — меньшая диагональ

α — острый угол

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в ромб через диагонали ( r ) :

Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :

Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :

Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :

2. Радиус вписанной окружности ромба, равен половине его высоты

a — сторона ромба

h — высота

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в ромб ( r ) :

Радиус вписанной окружности в правильный многоугольник

a — сторона многоугольника

N — количество сторон многоугольника

Формула радиуса вписанной окружности в правильный многоугольник, (r):

Формула нахождения радиуса вписанной окружности

Вычисление радиуса вписанной окружности ведется по формулам, которые зависят от фигуры и известных данных. Главным условием является тот факт, что фигура должна подходить под список тех, в которые можно вписать окружность.

Радиус — перпендикуляр, соединяющий центр окружности с любой точкой, лежащей на окружности. По длине радиус составляет половину диаметра.

Треугольник

Формула нахождения радиуса окружности, вписанной в треугольник через все стороны:

\(r=\sqrt{\frac{\left(p-a\right)\left(p-b\right)\left(p-c\right)}p},\)

где r — радиус,

a, b и c — стороны треугольника,

p — полупериметр, \(p=\frac{a+b+c}2.\)

Формула нахождения радиуса окружности, вписанной в треугольник через сторону и высоту:

\(r=\frac{b\times h}{b+\sqrt{4\times h^2+b^2}},\)

\(r=\frac{h\times\sqrt{a^2-h^2}}{a+\sqrt{a^2-h^2}},\)

где r — радиус,

a и b — стороны треугольника,

h — высота.

Равносторонний треугольник

Формула нахождения радиуса окружности, вписанной в равносторонний треугольник:

\(r=\frac a{2\sqrt3},\)

где r — радиус,

a — сторона треугольника.

Равнобедренный треугольник

Формула нахождения радиуса окружности, вписанной в равнобедренный треугольник через значения сторон:

\(r=\frac b2\sqrt{\frac{2a-b}{2a+b}},\)

где r — радиус,

a и b — стороны треугольника.

Формула нахождения радиуса окружности, вписанной в равнобедренный треугольник через сторону и угол:

\(r=A\times\frac{\sin\left(a\right)\times\cos\left(a\right)}{1+\cos\left(a\right)}= A\times\cos\left(a\right)\times\tan\left(\frac a2\right),\)

\(r=\frac b2\times\frac{\sin\left(a\right)}{1+\cos\left(a\right)}=\frac b2\times\tan\left(\frac a2\right),\)

где r — радиус,

A и b — стороны треугольника,

a — угол при основании.

Прямоугольный треугольник

Формула нахождения радиуса окружности, вписанной в прямоугольный треугольник:

\(r=\frac{a\times b}{a+b+c}=\frac{a+b-c}2,\)

где r — радиус,

a и b — катеты треугольника,

c — гипотенуза.

Равнобедренная трапеция

Формула нахождения радиуса окружности, вписанной в равнобедренную трапецию:

\(r=\frac h2=\frac{\sqrt{c\times b}}2,\)

где r — радиус,

с — нижнее основание,

b — верхнее,

а — боковые стороны,

h — высота.

Формула нахождения радиуса окружности, вписанной в квадрат:

\(r=\frac a2,\)

где r — радиус,

а — сторона квадрата.

Ромб

Формула нахождения радиуса окружности, вписанной в ромб через значения диагоналей:

\(r=\frac{D\times d}{4\times a}=\frac{D\times d}{2\sqrt{D^2+d^2}}.\)

Формула нахождения радиуса окружности, вписанной в ромб через значения стороны и угла:

\(r=\frac{a\times\sin\left(a\right)}2.\)

Формула нахождения радиуса окружности, вписанной в ромб через диагональ и угол:

\(r=\frac d2\times\cos\left(\frac a2\right)=\frac d{2\sqrt2}\times\sqrt{1+\cos\left(a\right)},\)

\(r=\frac D2\times\sin\left(\frac a2\right)=\frac D{2\sqrt2}\times\sqrt{1-\cos\left(a\right)}.\)

Формула нахождения радиуса окружности, вписанной в ромб через диагональ и сторону:

\(r=\frac{D\sqrt{a^2-{\displaystyle\frac{D^2}4}}}{2a},\)

\(r=\frac{d\sqrt{a^2-{\displaystyle\frac{d^2}4}}}{2a}.\)

Формула нахождения радиуса окружности, вписанной в ромб через высоту:

\(r=\frac h2,\)

где r — радиус,

а — сторона ромба,

D — большая диагональ,

d — меньшая диагональ,

a — острый угол,

h — высота.

Многоугольник

Формула нахождения радиуса окружности, вписанной в правильный многоугольник:

\(r=\frac a{2\times\tan\left({\displaystyle\frac{180^\circ}N}\right)},\)

где r — радиус,

N — количество сторон многоугольника.

Правильный n-угольник — формулы

Формулы длины стороны правильного n-угольника

1. Формула стороны правильного n-угольника через радиус вписанной окружности:

а = 2г тг	180°
н

а = 2г тг	π
н

2. Формула стороны правильного n-угольника через радиус описанной окружности:

а = 2 R sin	180°
н

а = 2 R sin	π
н

Формула радиуса вписанной окружности n-угольника через длину стороны:

г = а : (2tg	180°	)
н

г = а : (2tg	π	)
н

Формула радиуса описанной окружности n-угольника через длину стороны:

R = а : (2sin	180°	)
н

R = а : (2sin	π	)
н

Формулы площади правильного n-угольника

1. Формула площади n-угольника через длину стороны:

С =	на2	кТГ	180°
4	н

2. Формула площади n-угольника через радиус вписанной окружности:

С =	№2 тг	180°
н

3. Формула площади n-угольника через радиус описанной окружности:

С =	nR2	грех	360°
2	н

Формула периметра правильного n-угольника:

П = нет данных

Особенности расчета многоугольников с большим количеством сторон

При расчете многоугольника с большим количеством сторон возможны определенные сложности. Во-первых, чем больше количество сторон, тем сложнее измерить их длину точно. Это может привести к неточностям при расчетах.

Во-вторых, при увеличении количества сторон, радиус вписанной окружности уменьшается, что делает измерение его длины более трудным. Также необходимо учитывать, что при увеличении количества сторон увеличивается и площадь многоугольника, что также может усложнить расчеты.

Для решения этих проблем можно использовать различные методы, например, использовать приближенные значения длин сторон или использовать специальное программное обеспечение для точного расчета многоугольников с большим количеством сторон.

Кроме того, при расчетах многоугольников с большим количеством сторон, важно учитывать правильность его формы и точность измерений. В некоторых случаях, для получения более точных результатов, может потребоваться обратиться к специалистам в области геометрии и математики

Формула расчета стороны многоугольника

Для расчета стороны многоугольника, зная радиус вписанной окружности, можно воспользоваться формулой:

где:

• s — длина стороны многоугольника
• r — радиус вписанной окружности
• n — количество углов и сторон многоугольника

Эта формула основана на теореме тангенсов в геометрии.

Также, если известен диаметр вписанной окружности, то формула расчета стороны многоугольника будет иметь вид:

где d — диаметр вписанной окружности.

Важно учитывать, что эти формулы справедливы только для правильных многоугольников, в которых все стороны и углы равны. Для расчета длины описанной окружности многоугольника, также можно использовать следующую формулу:

Для расчета длины описанной окружности многоугольника, также можно использовать следующую формулу:

где C — длина описанной окружности многоугольника.

Эти формулы могут быть полезны при решении задач по геометрии и строительству, а также при проектировании многоугольных объектов, например, зданий или мебели.

Формула площади многоугольника через радиус вписанной окружности

Нарисуем многоугольник A₁A₂A₃A₄A₅, не обязательно правильный, но такой, в который можно вписать окружность. Напомню, что вписанной называется окружность, которая касается всех сторон многоугольника. На рисунке это зелёная окружность с центром в точке O:

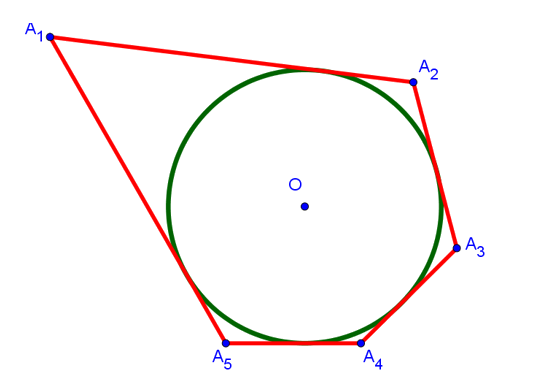
Мы взяли здесь для примера 5-угольник. Но на самом деле это не имеет существенного значения, поскольку дальнейшее доказательство справедливо и для 6-угольника и для 8-угольника и вообще для любого сколь угодно «угольника».

Если соединить центр вписанной окружности со всеми вершинами многоугольника, то он разобьётся на столько треугольников, сколько вершин в данном многоугольнике. В нашем случае: на 5 треугольников. Если же соединить точку O со всеми точками касания вписанной окружности со сторонами многоугольника, то получится 5 отрезков (на рисунке снизу это отрезки OH₁, OH₂, OH₃, OH₄ и OH₅), которые равны радиусу окружности и перпендикулярны сторонам многоугольника, к которым они проведены. Последнее справедливо, поскольку радиус, проведенный в точку касания, перпендикулярен касательной:

Как же найти площадь нашего описанного многоугольника? Ответ прост. Нужно сложить площади всех полученных в результате разбиения треугольников:

Рассмотрим, чему равна площадь треугольника . На рисунке снизу он выделен жёлтым цветом:

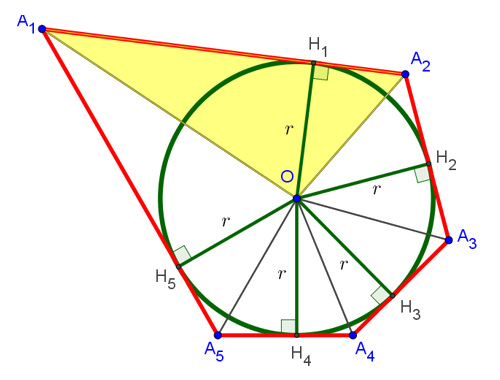
Она равна половине произведения основания A₁A₂ на высоту OH₁, проведённую к этому основанию. Но, как мы уже выяснили, эта высота равна радиусу вписанной окружности. То есть формула площади треугольника принимает вид: , где r — радиус вписанной окружности. Аналогично находятся площади всех оставшихся треугольников. В результате искомая площадь многоугольника оказывается равна:

Видно, что во всех слагаемых этой суммы ест общий множитель , который можно вынести за скобки. В результате получится вот такое выражение:

То есть в скобках осталась просто сумма всех сторон многоугольника, то есть его периметр P. Чаще всего в этой формуле выражение заменяют просто на p и называют эту букву «полупериметром». В результате, окончательная формула принимает вид:

То есть площадь многоугольника, в который вписана окружность известного радиуса, равна произведению этого радиуса на полупериметр многоугольника. Это и есть тот результат, в которому мы стремились.

Отметит напоследок, что в треугольник, который является частным случаем многоугольника, всегда можно вписать окружность. Поэтому для треугольника эту формулу можно применять всегда. Для остальных многоугольников, с количеством сторон большим 3, сперва нужно убедиться, что в них можно вписать окружность. Если это так, можно смело использовать эту простую формулу и находить по ней площадь этого многоугольника.

Основные свойства правильного шестиугольника

1. У гексагона все внутренние углы равны между собой.
2. Каждый внутренний угол правильного шестиугольника равен 120°.
3. Все стороны гексагона равны между собой.
4. Радиус окружности, описанной около правильного шестиугольника, равен его стороне.
5. Большая диагональ правильного шестиугольника равна диаметру описанной около него окружности или сумме двух его сторон.
6. Меньшая диагональ правильного шестиугольника в \(\sqrt3\)раз больше его стороны.
7. Меньшая диагональ правильного шестиугольника и две его противолежащие стороны перпендикулярны друг другу.
8. Меньшая диагональ правильного шестиугольника равна удвоенному радиусу вписанной в него окружности.
9. Правильный шестиугольник замещает плоскость, это значит заполняет ее без пробелов и наложений.
10. Диагонали правильного шестиугольника пересекаются в одной точке и делят его на 6 равных равносторонних треугольников. Высота этих треугольников равна радиусу вписанной в правильный шестиугольник окружности.
11. При поворотах относительно центра на угол, кратный 60°, правильный шестиугольник переходит в себя.
12. Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями — прямоугольный. Гипотенузой такого треугольника является большая диагональ. Его острые углы равны 30° и 60°.

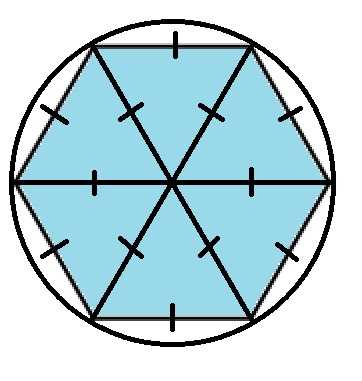
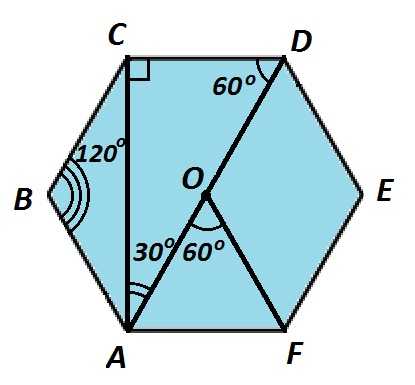
У изображенного правильного шестиугольника ∠А=∠В=∠С=∠D=∠Е=∠F=120°. Стороны равны между собой АВ=ВС=СD=DE=EF=FA. Точка О — центр пересечения диагоналей. Большая диагональ AD=2АВ. Меньшая диагональ \(СА=\sqrt3·АВ\).

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Теорема 1

В любой правильный шестиугольник можно вписать окружность, и притом только одну.

Следствие из теоремы:

1. Центры вписанной и описанной окружности у правильного шестиугольника (как и у любого правильного многоугольника) совпадают.
2. Радиус вписанной окружности равен перпендикуляру, проведенному из центра к любой стороне правильного шестиугольника.

Как найти площадь многоугольника

Все, что имеет больше двух углов, является многоугольником, в том числе и треугольник. Рассмотрим, как найти площадь многоугольников.

1

Как найти площадь многоугольника – треугольник

• S = 1/2×h×b, где h – высота, а b – сторона.
• S = 1/2 a×b×sinα, где а и b – стороны треугольника, а sinα – синус угла между ними.
• S = √p×(p-a)×(p-b)×(p-c), где p – половина периметра, а, b, c – стороны. Если известны все стороны треугольника, то найти площадь можно именно по этой формуле.
• S = r×p, где r – радиус вписанной окружности, а p – половина периметра. Если в треугольник вписана окружность, то для нахождения площади можно использовать эту формулу.
• S = abc/4R, где a, b, c – стороны треугольника, а R – радиус описанной окружности. Если треугольник вписан в окружность, для нахождения площади треугольника можно использовать эту формулу.

Прямоугольный треугольник

• S = 1/2×ab, где a и b – катеты прямоугольного треугольника.
• S = d×e, где d и e отрезки гипотенузы, образованные при касании вписанной окружности об гипотенузу.
• S = (p-a)×(p-b), где p – половина периметра, а и b – катеты.

Равнобедренный треугольник

• S = 1/2×a²×sina, где а – бедро треугольника, sina же – угол между бедрами.
• S = b²/4tgα/2, где b – основание треугольника, а tgα – угол между бедрами.

Равносторонний треугольник

• S = √3×a²/4, где а – сторона треугольника (любая, так как в равностороннем треугольнике все стороны равны).
• S = 3√3×R²/4, где R – радиус окружности, в которую вписан треугольник.
• S = 3√3×r², где r – радиус окружности, которая вписана в треугольник.
• S = h²/√3, где h – высота равностороннего треугольника.

2

Как найти площадь многоугольника – квадрат

• S = a², а – сторона квадрата. Так как все стороны квадрата равны, достаточно умножить одну его сторону на другую.
• S = d²/2, где d – диагональ квадрата.

3

Как найти площадь многоугольника – прямоугольник

• S = a×b, где a и b – стороны прямоугольника. Так как противолежащие стороны в прямоугольнике равны, достаточно умножить одну его сторону (длину) на не противолежащую, перпендикулярную сторону (ширину).
• S = a²+b²=c², где a – ширина, b – длина, а c – диагональ. Диагональ делит прямоугольник на два прямоугольных треугольника и если в условии задачи дана одна сторона прямоугольника и его диагональ, несложно будет найти и третью сторону, использую теорему Пифагора. После того как мы найдем эту сторону, ищем площадь по стандартной формуле a×b. Пример: Ширина прямоугольника – 3см, диагональ – 5 см. Найти площадь. Пишем 3² + x² = 5².  x² = 16 => x = 4. S = a×b = 3×4=12. Ответ: S прямоугольника = 12см²

4

Как найти площадь многоугольника – трапеция

• S = (a+b)×h/2, где a – маленькое, b – большое основание трапеции, h – высота.
• S = h×m, где h – высота, m – средняя линия трапеции, равная половине суммы оснований – 1/2×(a+b).
• S = 1/2×d1×d2×sinα, где d1 и d2 – диагонали трапеции, а sinα – синус угла между ними.
• S = a+b/2×√c²-((b-a)²+c²-d²/2(b-a))², где a и b – основания трапеции, c и d – остальные две стороны.

S = 4r²/sinα, где r – радиус вписанной окружности, а sinα – синус угла между стороной и основанием.

5

Площадь правильного многоугольника

• S = r×p = 1/2×r×n×a, где r – радиус вписанной окружности, p – половина периметра. Для того чтобы найти площадь любого правильного многоугольника, нужно разбить его на равные треугольники с общей вершиной в центре вписанной окружности.
• S = n×a²/4tg(360°/2n), где n – число сторон правильного многоугольника, а – длина стороны.Также вычислить площадь правильного многоугольника поможет данный онлайн сервис. Просто вставьте нужное значение и получите ответ.

6

Площадь неправильного многоугольника

Площадь неправильного многоугольника можно найти с помощью координат его вершин. Если в условии задачи даны вышеупомянутые координаты, то выполняем следующее:

• Составляем таблицу указывая букву, обозначающую вершину и соответствующие координаты (x; y).
• Умножаем значение x одной вершины на значение y второй и так далее.
• Складываем все значение, получаем какое-то число.

Составляем точно такую таблицу, по такому же принципу умножаем y координату одной вершины на x координату второй, складываем получившиеся значения.

От суммы значений первой таблицы отнимаем сумму значений второй таблицы.

Полученное число делим на 2 и тем самым находим площадь неправильного многоугольника.

Первая полоса

Беременность

Как не набрать лишний вес во время беременности