Как найти радиус вписанной в квадрат окружности: через сторону, диагональ

Примеры задач

Задание №1.
Дан прямой цилиндр, площадь основания которого 12,56 см 2 . Необходимо вычислить полную площадь цилиндра, если его высота равна 3 см.

Решение. Необходимо воспользоваться формулой для полной площади кругового прямого цилиндра. Но в ней не хватает данных, а именно радиуса основания. Зато известна площадь круга. Из нее легко вычислить радиус.

Он оказывается равным квадратному корню из частного, которое получается от деления площади основания на пи. После деления 12,56 на 3,14 выходит 4. Квадратный корень из 4 — это 2. Поэтому радиус будет иметь именно такое значение.

Ответ: S пол = 50,24 см 2 .

Задание №2.
Цилиндр с радиусом 5 см пресечен плоскостью, параллельной оси. Расстояние от сечения до оси равно 3 см. Высота цилиндра — 4 см. Требуется найти площадь сечения.

Решение. Форма сечения — прямоугольная. Одна его сторона совпадает с высотой цилиндра, а другая равна хорде. Если первая величина известна, то вторую нужно найти.

Для этого следует сделать дополнительное построение. В основании проводим два отрезка. Оба они будут начинаться в центре окружности. Первая будет заканчиваться в центре хорды и равняться известному расстоянию до оси. Вторая — на конце хорды.

Получится прямоугольный треугольник. В нем известны гипотенуза и один из катетов. Гипотенуза совпадает с радиусом. Второй катет равен половине хорды. Неизвестный катет, умноженный на 2, даст искомую длину хорды. Вычислим его значение.

Для того чтобы найти неизвестный катет, потребуется возвести в квадрат гипотенузу и известный катет, вычесть из первого второе и извлечь квадратный корень. Квадраты равны 25 и 9. Их разность — 16. После извлечения квадратного корня остается 4. Это искомый катет.

Хорда будет равна 4 * 2 = 8 (см). Теперь можно вычислить площадь сечения: 8 * 4 = 32 (см 2).

Ответ: S сеч равна 32 см 2 .

Задание №3.
Необходимо вычислить площадь осевого сечения цилиндра. Известно, что в него вписан куб с ребром 10 см.

Решение. Осевое сечение цилиндра совпадает с прямоугольником, который проходит через четыре вершины куба и содержит диагонали его оснований. Сторона куба является образующей цилиндра, а диагональ основания совпадает с диаметром. Произведение этих двух величин даст площадь, которую нужно узнать в задаче.

Для поиска диаметра потребуется воспользоваться знанием того, что в основании куба — квадрат, а его диагональ образует равносторонний прямоугольный треугольник. Гипотенуза его является искомой диагональю фигуры.

Для ее расчета потребуется формула теоремы Пифагора. Нужно возвести в квадрат сторону куба, умножить ее на 2 и извлечь квадратный корень. Десять во второй степени — это сто. Умноженное на 2 — двести. Квадратный корень из 200 равен 10√2.

Сечение — это снова прямоугольник со сторонами 10 и 10√2. Его площадь легко сосчитать, перемножив эти значения.

Ответ. S сеч = 100√2 см 2 .

Вписанная окружность в квадрат

Одной из задач Всероссийской проверочной работы (ВПР) по математике может быть поиск диагонали вписанной в квадрат окружности. Чтобы решить эту задачу, необходимо знать свойства вписанных окружностей.

Вписанная окружность — это окружность, которая полностью помещается внутри фигуры. В случае с квадратом, вписанная окружность проходит через каждую вершину квадрата.

Мы можем использовать знание о свойствах квадратов, чтобы найти диагональ вписанной окружности. Зная, что в квадрате все стороны равны, мы можем сделать вывод, что диагональ квадрата является диаметром вписанной окружности.

Диагональ квадрата можно найти с помощью теоремы Пифагора или применяя знание о связи диагонали квадрата с его сторонами. Затем, зная значение диагонали, мы можем найти диаметр вписанной окружности, который будет равен длине диагонали квадрата.

Таким образом, решая задачу о диагонали вписанной в квадрат окружности, мы применяем знания о свойствах вписанных окружностей и квадратов. Задачи такого типа помогают развить логическое мышление и навыки применения математических знаний в практических ситуациях.

Как определить, что окружность вписана в квадрат?

Математика предлагает нам методы и инструменты для решения различных задач. Когда речь идет о вписанных фигурах, в том числе круге и квадрате, мы также можем применить определенные правила и формулы. Как же определить, что окружность точно вписана в квадрат?

Одним из основных свойств вписанной окружности является то, что центр окружности лежит на диагонали квадрата. Диагональ квадрата — это отрезок, соединяющий две противоположные вершины. Таким образом, чтобы определить, что окружность вписана в квадрат, необходимо проверить, что центр окружности лежит на диагонали.

Для наглядности можно использовать координаты вершин квадрата. Если вершины квадрата имеют координаты (x1, y1), (x2, y2), (x3, y3) и (x4, y4), то диагональ будет проходить через точки ((x1+x3)/2, (y1+y3)/2) и ((x2+x4)/2, (y2+y4)/2).

При заданном центре окружности с координатами (a, b) можно проверить, лежит ли он на диагонали, подставив эти координаты в уравнение прямой, проходящей через две точки диагонали. Если уравнение выполняется, это означает, что окружность вписана в квадрат.

Итак, чтобы определить, что окружность вписана в квадрат, необходимо проверить, что центр окружности лежит на диагонали квадрата. Это можно сделать, подставив координаты центра окружности в уравнение прямой, проходящей через две точки диагонали. Если уравнение выполняется, значит, окружность действительно вписана в квадрат.

Свойства вписанной окружности в квадрат

В квадрате можно вписать окружность таким образом, чтобы ее центр совпадал с центром квадрата. Такая окружность называется вписанной в квадрат. В математике возникает задача: как найти диагональ вписанной в квадрат окружности? Данная проблема является одной из тем в Всероссийской проверочной работы по математике.

Для решения этой задачи существует несколько подходов. Один из них основан на использовании свойств вписанной окружности. Например, известно, что вписанные в квадрат окружности делят его диагональ на две равные части. Это означает, что диагональ квадрата является диаметром вписанной в него окружности.

Еще одно свойство вписанной окружности заключается в том, что длина любого ее диаметра равна стороне квадрата.

Таким образом, если известна длина стороны квадрата, то можно легко найти диагональ вписанной в него окружности, так как она будет равна стороне квадрата.

Важно учитывать, что во Всероссийской проверочной работе по математике могут быть предложены задачи, в которых необходимо не только найти диагональ вписанной окружности, но и решить ее с использованием других математических методов и свойств квадрата и окружности. Поэтому рекомендуется подготовиться к ВПР, изучив все соответствующие темы в программе по математике

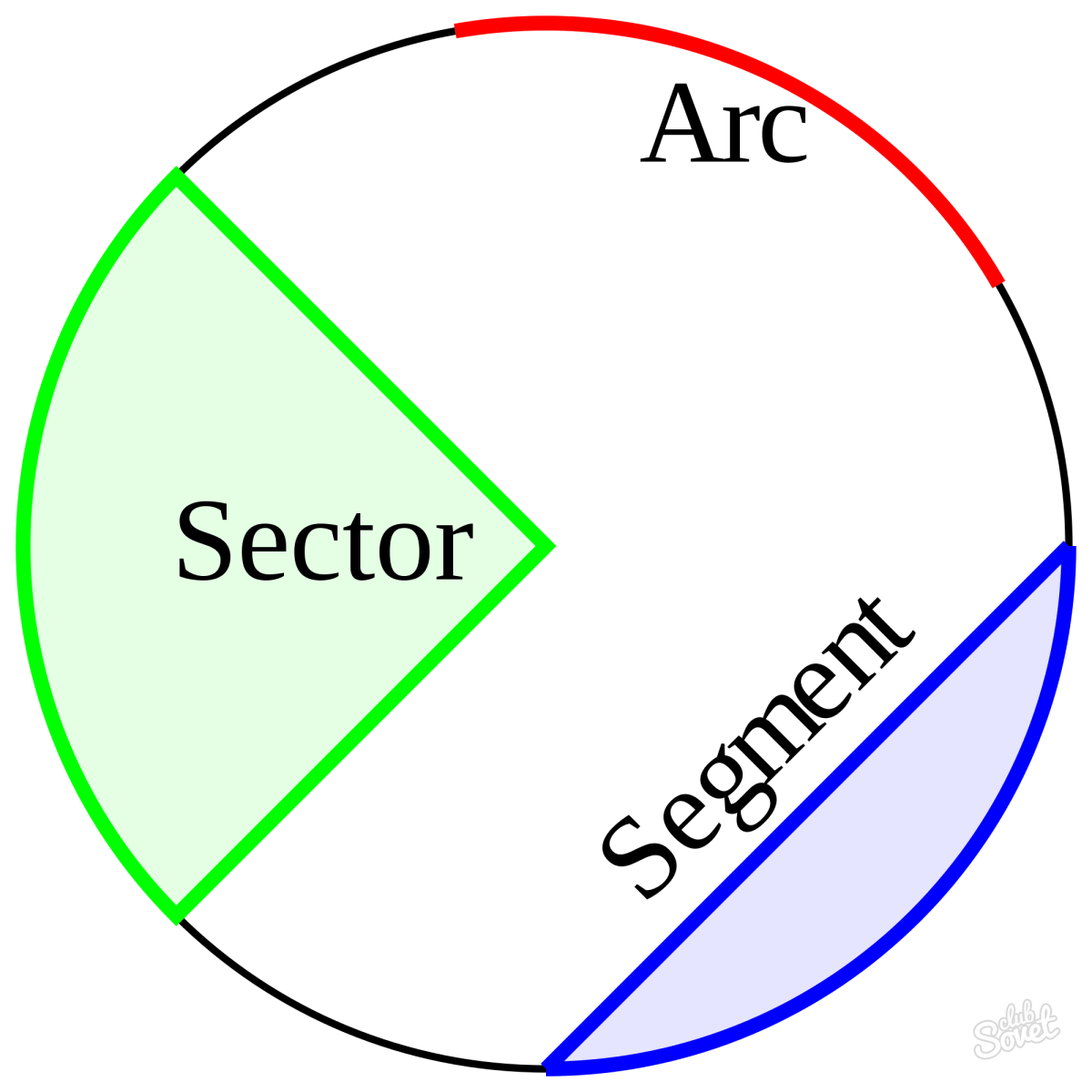
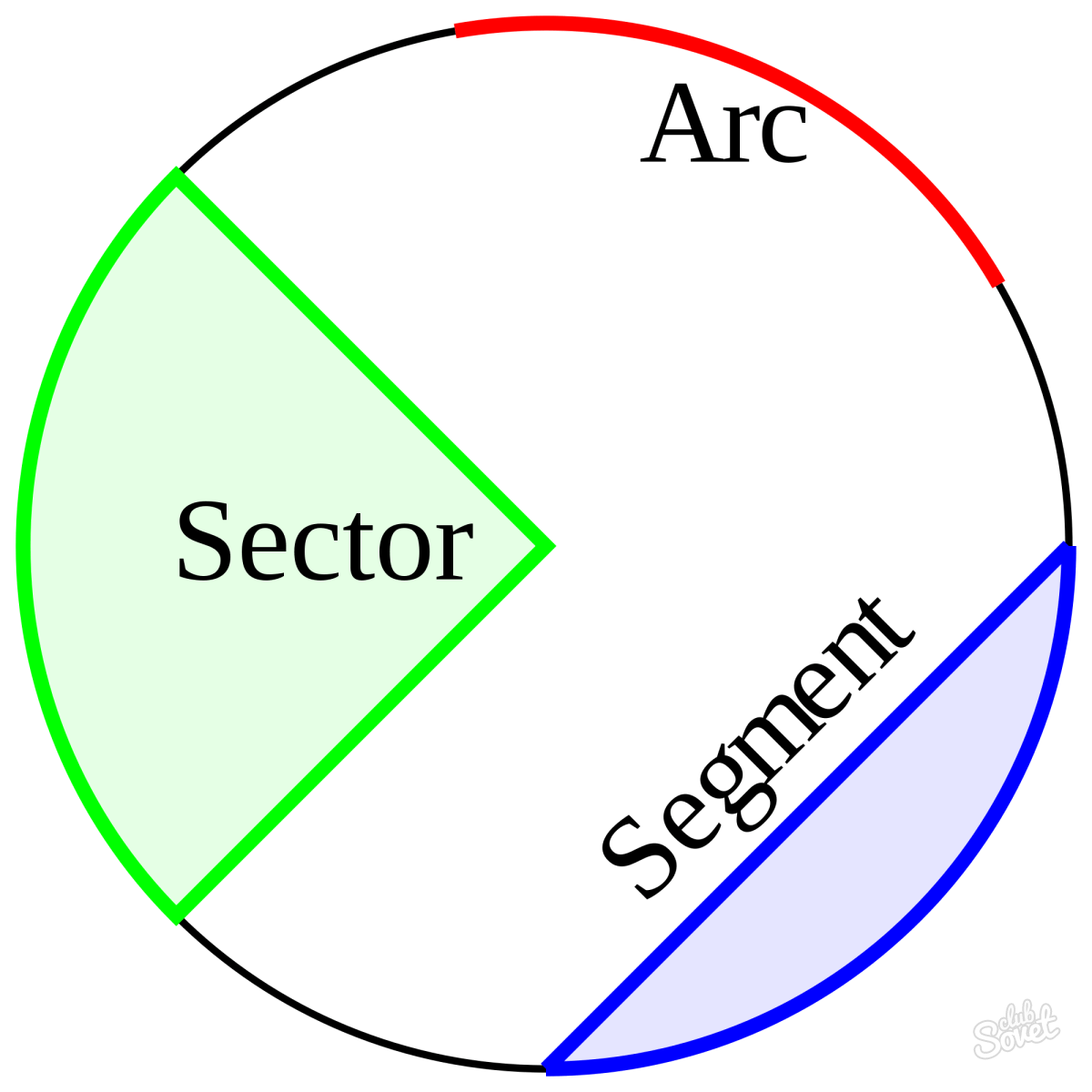
Площадь сектора круга

Сектор – это часть круга, ограниченная 2 радиусами и дугой между ними. Чтобы узнать его площадь, нужно измерить угол сектора. После этого необходимо составить дробь, в числителе которой будет значение угла сектора, а в знаменателе – 360. Чтобы высчитать площадь сектора, значение, полученное в результате деления дроби, нужно умножить на площадь круга, вычисленную по одной из вышеперечисленных формул.

Чтобы формула нахождения радиуса вписанной окружности в квадрат r была правильно рассчитана, необходимо изначально вспомнить какими свойствами обладает данная фигура. У квадрата:

• все углы прямые, то есть, равны 90°;
• все стороны, как и углы, равны;
• диагонали равны, точкой пересечения бьются строго пополам и пересекаются под углом 90°.

При этом вписанная в выпуклый многоугольник окружность обязательно касается всех его сторон. Обозначим квадрат ABCD
, точку пресечения его диагоналей O
. Как видно на рисунке 1, пересечение линий АС
и ВD
дают равнобедренный треугольник АОВ
, в котором стороны АО
=ОВ
, углы ОАВ
=АВО
=45°, а угол АОВ
=90°. Тогда радиусом вписанной окружности в квадрат будет не что иное, как высота ОЕ
полученного равнобедренного треугольника АОВ
.

Если предположить, что сторона квадрата равна у
, то формула нахождения радиуса вписанной окружности в квадрат будет выглядеть следующим образом:

Объяснение

: в равнобедренном треугольнике АОВ
высота ОЕ
или радиус r
делят основание АВ
пополам (свойства), образовывая при этом прямоугольный треугольник с прямым угол ОЕВ
. В маленьком треугольнике ЕВО
основание ОВ
образует со сторонами ОЕ
и ЕВ
углы по 45°. Значит треугольник ЕВО
еще и равнобедренный. Стороны ОЕ
и ЕВ
равны.

Для наглядности приведем численный пример нахождения величины радиуса вписанной окружности в квадрат со стороной равной 13 см. В данном случае значение вписанного радиуса будет равно:
Легко решить и обратную задачу. Предположим, что известен радиус вписанной окружности – 9 см, тогда анализируя пример нахождения величины радиуса вписанной окружности в квадрат, можно найти сторону квадрата:
Находим из этого уравнения неизвестное значение: .

Вокруг квадрата также можно описать окружность. В этом случае каждая вершина фигуры будет касаться окружности. Следующая формула нахождения радиуса описанной окружности около квадрата будет находиться еще проще. В этом случае R
описанной окружности будет равен половине диагонали квадрата. В буквенном виде формула выглядит так (рисунок 2):

Объяснение

: после проведения диагоналей ABCD
образовались два одинаковых прямоугольных треугольника АВС
= CDA
. Рассмотрим один из них. В треугольнике CAD
:

• угол CDA=90°;
• стороны AD
  =CD
  . Признак равнобедренного треугольника;
• угол DAC
  равен ACD
  . Они равны по 45°.

Чтобы найти в этом прямоугольном треугольнике гипотенузу АС
, необходимо воспользоваться теоремой Пифагора:, отсюда
Поскольку окружность касается вершин квадрата, а точка пересечения его диагоналей является центром описанной окружности (свойства), то отрезок ОС и будет радиусом окружности. Он является половинкой гипотенузы. Это утверждение вытекает из свойств равнобедренного треугольника или свойств диагоналей квадрата. Потому формула нахождения радиуса описанной окружности около квадрата в нашем случае имеет следующий вид:
Поскольку AD
=CD
, а свойства квадратного корня позволяют вынести одно из подкоренных выражений, тогда формула приобретает вид:

Численный пример нахождения величины радиуса описанной окружности около квадрата будет таким.
Предположим, что диагональ квадрата равна , тогда:

В ромбе

Им считается параллелограмм с одинаковой длиной сторон. Радиус окружности, вписываемой в него, можно рассчитать несколькими способами.

1. Чтобы сделать это правильно, найдите радиус вписанной окружности ромба, если известна площадь ромба, длина его стороны. Применяется формула r=S/(2Хa). К примеру, если площадь ромба составляет 200 мм кв., длина стороны 20 мм, то R=200/(2Х20), то есть, 5 мм.
2. Известен острый угол одной из вершин. Тогда необходимо использовать формулоу r=v(S*sin(α)/4). Например, при площади в 150 мм и известном угле в 25 градусов, R= v(150*sin(25°)/4) ≈ v(150*0,423/4) ≈ v15,8625 ≈ 3,983 мм.
3. Все углы в ромбе равны. В этой ситуации радиус окружности, вписанной в ромб, будет равен половине длины одной стороны данной фигуры. Если рассуждать по Евклиду, утверждающего, что сумма углов всякого четырёхугольника равна 360 градусов, то один угол будет равен 90 градусам; т.е. получится квадрат.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию

Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

В этой статье популярно объяснено, как найти радиус окружности, вписанной в квадрат. Теоретический материал поможет вам разобраться во всех связанных с темой нюансах. Прочитав этот текст, вы с легкостью сможете решать подобные задачи в дальнейшем.

Последние заданные вопросы в категории Математика

Математика 07.09.2023 07:28 4 Копьёва Ксения.

245*524+132281):(1295-54*18)

Ответов: 1

Математика 07.09.2023 07:28 23 Глухих Диана.

Растояние между городами 980 км. Первые 4 ч поезд шел со скоростью 80 км/ч. С какой скоростью поезд

Ответов: 1

Математика 07.09.2023 07:22 26 Алим Дамир.

покупатель в магазине истрател денег в 4 раза больше чем на рынке сколько всего истратил покупатель

Ответов: 1

Математика 07.09.2023 07:08 21 Чураева Алина.

Решение уравнения x*6=18000+24

Ответов: 2

Математика 07.09.2023 07:07 3 Багриновская Ольга.

Из шести девочек и трёх мальчиков надо выбрать одного ученика для дежурства в ш.к столовой . какова

Ответов: 1

Математика 07.09.2023 07:05 15 Шералиева Мерей.

8 квадратных дм 2 квадратных см-58 квадратных см 96 квадратных мм. Помогитееееее

Ответов: 1

Математика 07.09.2023 07:02 30 Ільницький Назар.

Длина школьного коридора 30,24 м,а ширина 5,12 м. Найдите его площадь в квадратных метрах.Ответ окру

Ответов: 2

Математика 07.09.2023 07:01 10 Макеев Олег.

Ширина прямоугольника 8 см, что на 3 см меньше длины. найдите площадь этого прямоугольника

Ответов: 1

Математика 07.09.2023 07:01 13 Немчёнок Илья.

Решите СРОЧНОООО НУЖНО НА ЗАВТРААА!!!! ПОЖАЛУЙСТА ПОЖАЛУЙСТА ПОЖАЛУЙСТА!! X составляет 20% от 42

Ответов: 1

Математика 07.09.2023 07:00 23 Красавина Дарья.

задача 3-клас. З 21 кг залізної руди до боли 7 кг заліза. Скільки кг заліза можна добути з 54 кг так

Ответов: 2

Вписанная окружность — в какую фигуру нельзя вписать

Для решения геометрических задач можно использовать различные формулы и приемы, которые помогут облегчить поиск искомых показателей. Один из способов найти различные неизвестные в многогранной фигуре – сделать это через вписанную окружность.

Вписанная окружность — окружность, которая лежит внутри угла и касается его сторон. Касание происходит в одной точке с каждой стороны. 

Вписанная в фигуру окружность, например, в треугольник или многоугольник, будет касаться всех его сторон. Это главное свойство окружности, которая будет называться вписанной. Сама фигура в таком случае называется описанной вокруг окружности.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Следствие 

Из этого следует, что вписанная окружность не будет таковой, если не будет касаться всех сторон фигуры.

Окружность точно можно вписать в следующие геометрические фигуры:

• треугольник;
• выпуклый правильный многоугольник;
• квадрат;
• равнобедренная трапеция;
• ромб.

При этом окружность в данные фигуры может быть вписана лишь единожды.

Четырехугольник является неоднозначной фигурой при процессе вписывания в нее окружности. Для того, чтобы окружность была вписанной в четырехугольник, суммы длин его противоположных сторон должны быть равны.

Окружность точно нельзя вписать в следующие геометрические фигуры:

• прямоугольник;
• параллелограмм (если он не является ромбом).

Ни один из видов данных фигур не сможет иметь вписанную окружность, так как она не сможет соприкасаться со всеми их сторонами, что является главным признаком вписанной окружности.

Как найти радиус описанной окружности

Предположим, что a, b, c — это стороны треугольника. Если знать их величины, то можно найти радиус описанной вокруг него окружности. Для этого сначала нужно найти полупериметр треугольника. Чтобы было легче для восприятия, обозначим его маленькой буквой p. Он будет равен половине суммы сторон. Его формула: p = (a + b + c) / 2.

Также вычислим произведение длин сторон. Для удобства обозначим его буквой S. Формула радиуса описанной окружности будет выглядеть так: R = S / (4 * √(p * (p — a) * (p — b) * (p — c)).

Рассмотрим пример задачи. У нас есть окружность, описанная вокруг треугольника. Длины ее сторон составляют 5, 6 и 7 см. Сначала вычисляем полупериметр. В нашей задаче он будет равен 9 сантиметрам. Теперь вычислим произведение длин сторон — 210. Подставляем результаты промежуточных расчетов в формулу и узнаем результат. Радиус описанной окружности равен 3,57 сантиметра. Записываем ответ, не забывая о единицах измерения.

Когда известен периметр квадрата

Периметр квадрата – это сумма длин всех его сторон. Вот его формула:

P = а + а + а + а                                            

Или

Р = а × 4

Чтобы найти площадь, мы возводим периметр в квадрат, и делим на 16:

S = Р² : 16

Где Р – это периметр.

Пример: 

Если периметр квадрата P равен 7 см, то площадь S равна:

S = 14² : 16 = 196 : 16 = 12,25 см²

Важно!

Задачу нельзя решить, если длина и ширина будут даны в разных единицах измерения. 

Например, мы знаем, что длина прямоугольника – 2 дм, а ширина – 13 см. Сможем ли мы вычислить площадь?

Чтобы найти площадь, нам надо длину умножить на ширину:

2 дм × 13 см

Если просто перемножить между собой цифры, то мы получим ответ 26. Но 26 чего? Сантиметров или дециметров? 26 – это неверный ответ. 

Мы знаем, что в одном дециметре десять сантиметров. Поэтому нам нужно сначала посчитать, сколько сантиметров будет в двух дециметрах:

2 дм = 2 × 10 = 20 см

Теперь мы можем вычислить площадь прямоугольника:

S = 20 × 13 = 260 см

Для правильного решения нужно перевести все данные к одной единице измерения – тогда всё получится.

О площадях наклонного кругового цилиндра

Что касается оснований, то там все формулы те же, ведь они по-прежнему круги. А вот боковая поверхность уже не дает прямоугольника.

Для расчета площади боковой поверхности наклонного цилиндра потребуется перемножить значения образующей и периметра сечения, которое будет перпендикулярно выбранной образующей.

Формула выглядит так:

S бок = х * Р,

где х — длина образующей цилиндра, Р — периметр сечения.

Сечение, кстати, лучше выбирать такое, чтобы оно образовывало эллипс. Тогда будут упрощены расчеты его периметра. Длина эллипса вычисляется по формуле, которая дает приблизительный ответ. Но его часто бывает достаточно для задач школьного курса:

l = π * (а + в),

где «а» и «в» — полуоси эллипса, то есть расстояния от центра до ближайшей и самой дальней его точек.

Площадь всей поверхности нужно вычислять с помощью такого выражения:

S пол = 2
π * r 2 + х * Р.

Окружность, вписанная в треугольник

Окружность, вписанная в треугольник, соприкасается с каждой стороной этой фигуры лишь в одной точке. В один треугольник возможно вписать лишь одну окружность.

Радиус такой окружности будет зависеть от следующих параметров треугольника:

1. Длин сторон треугольника.
2. Его площади.
3. Его периметра.
4. Величины углов треугольника.

Для того чтобы вычислить радиус вписанной окружности в треугольник, не всегда обязательно знать все перечисленные выше параметры, поскольку они взаимосвязаны между собой через тригонометрические функции.

Вычисление с помощью полупериметра

Чтобы рассчитать величину радиуса вписанной окружности в треугольник, необходимо учитывать следующие параметры:

1. Если известны длины всех сторон геометрической фигуры (обозначим их буквами a, b и c), то вычислять радиус придётся путём извлечения квадратного корня.
2. Приступая к вычислениям, необходимо добавить к исходным данным ещё одну переменную — полупериметр (р). Его можно рассчитать, сложив все длины и полученную сумму разделив на 2. p = (a+b+c)/2. Таким образом можно существенно упростить формулу нахождения радиуса.
3. В целом формула должна включать в себя знак радикала, под который помещается дробь, знаменателем этой дроби будет величина полупериметра р.
4. Числителем данной дроби будет представлять собой произведение разностей (p-a)*(p-b)*(p-c)
5. Таким образом, полный вид формулы будет представлен следующим образом: r = √(p-a)*(p-b)*(p-c)/p).

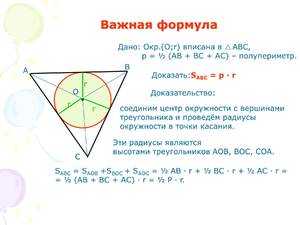
Вычисление с учётом площади треугольника

Если нам известна площадь треугольника и длины всех его сторон, это позволит найти радиус интересующей нас окружности, не прибегая к извлечению корней.

1. Для начала нужно удвоить величину площади.
2. Результат делится на сумму длин всех сторон. Тогда формула будет выглядеть следующим образом: r = 2*S/(a+b+c).
3. Если воспользоваться величиной полупериметра, можно получить совсем простую формулу: r = S/p.

Расчёт с помощью тригонометрических функций

Если в условии задачи присутствует длина одной из сторон, величина противоположного угла и периметр, можно воспользоваться тригонометрической функцией — тангенсом. В этом случае формула расчёта будет иметь следующий вид:

r = (P /2- a)* tg (α/2), где r — искомый радиус, Р — периметр, а — значение длины одной из сторон, α — величина противоположного стороне, а угла.

Радиус окружности, которую необходимо будет вписывать в правильный треугольник, можно найти по формуле r = a*√3/6.