Таблица основных формул дифференцирования

Правила дифференцирования производной

Чаще всего при нахождении производной требуется не просто посмотреть в таблицу производных, а вначале применить правила дифференцирования и доказательство производной произведения, и только потом использовать таблицу производных элементарных функций.

1. Постоянная выносится за знак производной

$(Cu)’=Cu’$,

$C$ – постоянная (константа).

Пример 1

Продифференцировать функцию $y=7x^4$.

Решение.

Находим $y’=(7x^4 )’$. Выносим число $7$ за знак производной, получаем:

$y’=(7x^4 )’=7(x^4 )’=$

используя таблицу, необходимо находить значение производной степенной функции:

$=7 \cdot 4x^3=$

Преобразуем результат к принятому в математике виду:

$=28x^3$.

Ответ: $28x^3$.

2. Производная суммы (разницы) равна сумме (разнице) производных:

$(u \pm v)’=u’ \pm v’$.

Пример 2

Продифференцировать функцию $y=7+x-5x^3+4 \sin x-9\sqrt{x^2}+\frac{4}{x^4} -11\cot x$.

Решение.

$y’=(7+x-5x^5+4 \sin x-9\sqrt{x^2}+\frac{4}{x^4} -11\cot x)’=$

применим правило дифференцирования производной суммы и разницы:

$=(7)’+(x)’-(5x^5 )’+(4 \sin x )’-(9\sqrt{x^2})’+(\frac{4}{x^4} )’-(11\cot x)’=$

отметим, что при дифференцировании все степени и корни необходимо преобразовать к виду $x^{\frac{a}{b}}$;

вынесем все постоянные за знак производной:

$=(7)’+(x)’-(5x^5 )’+(4\sin x )’-(9x^{\frac{2}{5}} )’+(4x^{-4} )’-(11\cot x)’=$

$=(7)’+(x)’-5(x^5 )’+4(\sin x )’-9(x^{\frac{2}{5}} )’+4(x^{-4} )’-11(\cot x)’=$

разобравшись с правилами дифференцирования, некоторые из них (например, как последние два) применяются одновременно во избежание переписывания длинного выражения;

мы получили выражение из элементарных функций, стоящих под знаком производной; воспользуемся таблицей производных:

$=0+1-5 \cdot 5x^4+4\cos x-9 \cdot \frac{2}{5} x^{-\frac{3}{5}}+12x^{-5}-11 \cdot \frac{-1}{\sin^2 x}=$

преобразуем к виду, принятому в математике:

$=1-25x^4+4 \cos x-\frac{18}{5\sqrt{x^3}}+\frac{12}{x^5} +\frac{11}{\sin^2 x}$

Обратим внимание, что при нахождении результата принято слагаемые с дробными степенями преобразовать в корни, а с отрицательными – в дроби. Ответ: $1-25x^4+4 \cos x-\frac{18}{5\sqrt{x^3}}+\frac{12}{x^5} +\frac{11}{\sin^2 x}$

Ответ: $1-25x^4+4 \cos x-\frac{18}{5\sqrt{x^3}}+\frac{12}{x^5} +\frac{11}{\sin^2 x}$.

3. Формула производной произведения функций:

$(uv)’=u’ v+uv’$.

Пример 3

Продифференцировать функцию $y=x^{11} \ln x$.

Решение.

Сначала применим правило вычисления производной произведения функций, а затем используем таблицу производных:

$y’=(x^{11} \ln x )’=(x^{11} )’ \ln x+x^{11} (\lnтx )’=11x^{10} \ln x+x^{11} \cdot \frac{1}{x}=11x^{10} \ln x-\frac{x^{11}}{x}=11x^{10} \ln x-x^{10}=x^{10} (11 \ln x-1)$.

Ответ: $x^{10} (11 \ln x-1)$.

4. Формула производной частной функции:

$(\frac{u}{v})’=\frac{u’ v-uv’}{v^2}$.

Пример 4

Продифференцировать функцию $y=\frac{3x-8}{x^5-7}$.

Решение.

$y’=(\frac{3x-8}{x^5-7})’=$

по правилам приоритета математических операций сначала выполним деление, а потом сложение и вычитание, поэтому применим сначала правило вычисления производной частного:

$=\frac{(3x-8)’ (x^5-7)-(3x-8) (x^5-7)’}{(x^5-7)^2} =$

применим правила производных суммы и разности, раскроем скобки и упростим выражение:

$=\frac{3(x^5-7)-5x^4 (3x-8)}{(x^5-7)^2} =\frac{3x^5-21-15x^5+40x^4}{(x^5-7)^2} =\frac{-12x^5+40x^4-21}{(x^5-7)^2}$ .

Ответ: $\frac{-12x^5+40x^4-21}{(x^5-7)^2}$.

Пример 5

Продифференцируем функцию $y=\frac{x^7-2x+3}{x}$.

Решение.

Функция y является частным двух функций, поэтому можно применить правило вычисления производной частного, но в таком случае получим громоздкую функцию. Для упрощения данной функции можно почленно разделить числитель на знаменатель:

$y=\frac{x^7-13x+9}{x}=x^6-13+\frac{9}{x}$.

Применим к упрощенной функции правило дифференцирования суммы и разности функций:

$y’=(x^6-13+\frac{9}{x})’=(x^6 )’+(-13)’+9(x^{-1} )’=6x^5+0+9 \cdot (-x^{-2})=$

$=6x^5-\frac{9}{x^2}$.

Ответ: $6x^5-\frac{9}{x^2}$.

Функция f(x)=x^3

Пример 1 Дано: 

Найти .

Зафиксируем точку  и найдем значение производной от конкретной функции в конкретной точке. Действуем по алгоритму.

1)Вычисляем значение . Иллюстрируем все это графиком.

Рис. 1. Кубическая парабола.

Зафиксировав точку , вычислим значение функции в этой точке. Получим .

2) Даем аргументу приращение  ,получаем   — новое значение аргумента.

Примечание. В данном случае приращение положительное. Можно дать приращение отрицательное, тогда функция будет либо увеличиваться, либо уменьшаться

Важно, что –любое

3) Вычислить значение функции в новой точке , подставив эту точку в функцию.

.

4) Найдем , то есть разность между значением функции в новой точке минус значение функции в старой точке.

.

Имеем две точки: значение аргумента  и значение функции в точке , новое значение аргумента и значение функции при новом значении аргумента. Разность этих значений функции дает .

5) Найдем разностное отношение

.

Знаменатель для всех функций один и тот же, — приращение аргумента, а числитель – свой для каждой функции. Получили разностное отношение. Далее надо упростить его, сократить на  и сделать дальнейший анализ.

Упрощать в данном случае можно по-разному. Можно применить формулу или куб суммы, или разность кубов. Напомним, что

. В данном случае  — это ,  — это . Имеем

Раскрывая скобки, получили многочлен. Приведем подобные члены. Дальше надо преобразовать так, чтобы  сократить. Вынесем за скобки, получим    Теперь можно сократить на , ведь , оно не равно нулю. Имеем соотношение следующего вида

. Осталось узнать, что происходит, когда . В данном случае второй член выражения  пропадет, и третий член пропадет. Останется , то есть .

Результат

, то есть смысл такой: 3 выносим как сомножитель и показатель уменьшили на единицу.

Итак, зафиксировали точку , нашли производную от конкретной функции в конкретной точке . Точка  может быть любая.

Ответ: .

Итак, мы зафиксировали функцию  — кубическую параболу. Была задача: найти производную этой функции в конкретной точке  . Мы зафиксировали точку  и действовали по алгоритму, который был изложен в общем виде, и применен к данной функции. Этот алгоритм можно применять к любой функции, а именно: вычислить значение функции в точке , подставив значение  в закон соответствия, то есть в функцию, дать приращение аргумента, найти значение функции при новом значении аргумента и получить приращение функции, то есть разность между  значениями функции в новой точке и старой. Далее, надо найти разностное отношение , упростить его так, чтобы вынести   за скобку и сократить на . В результате получится выражение, члены которого зависят от  и не зависят от него. Если члены, которые зависят от  прямо пропорциональны ему, то они при  стремятся к нулю, то есть пропадают. Остаются только члены, которые не зависят от . Таким образом получим значение производной.

Для знакомых с пределами  .

Важно понять, что есть члены с  члены  и члены без . При этом члены с  пропадают, остается то, что называется производной

Итак, производная от кубической функции в любой точке  — это .

Производная степенной функции.

Формула производной степенной функции имеет вид , где показатель степени p – любое действительное число.

Докажем сначала формулу для натурального показателя степени, то есть, для p = 1, 2, 3, …

Будем пользоваться определением производной. Запишем предел отношения приращения степенной функции к приращению аргумента:

Для упрощения выражения в числителе обратимся к формуле бинома Ньютона:

Следовательно,

Этим доказана формула производной степенной функции для натурального показателя.

При доказательстве формулы для любого действительного p, отличного от нуля, воспользуемся логарифмической производной (не путайте с производной логарифмической функции). Для понимания процесса, рекомендуем сначала ознакомиться с , а также разобраться с разделами теории производная неявно заданной функции и производная сложной функции.

Следует рассмотреть два случая: при положительных x и отрицательных x.

Сначала будем полагать . В этом случае . Выполним логарифмирование равенства по основанию e и применим свойство логарифма:

Пришли к неявно заданной функции. Находим ее производную:

Осталось провести доказательство для отрицательных x.

Когда показатель p представляет собой четное число, то степенная функция определена и при , причем является четной (смотрите раздел основные элементарные функции, их свойства и графики). То есть, . В этом случае и также можно использовать доказательство через логарифмическую производную.

Когда показатель p представляет собой нечетное число, то степенная функция определена и при , причем является нечетной. То есть, . В этом случае и логарифмическую производную использовать нельзя. Для доказательства формулы в этом случае можно воспользоваться правилами дифференцирования и правилом нахождения производной сложной функции:

Последний переход возможен в силу того, что если p — нечетное число, то p-1 либо четное число, либо нуль (при p=1), поэтому, для отрицательных x справедливо равенство .

Таким образом, формула производной степенной функции доказана для любого действительного p.

Пример.

Найти производные функций .

Решение.

Первую и третью функцию приведем к табличному виду , используя свойства степени, и применим формулу производной степенной функции:

Задача 3

Дано: 

Найти: тан­генс угла на­кло­на ка­са­тель­ной к кри­вой  в точ­ках: а) ; б) ; в)

Ре­ше­ние

На ри­сун­ке 5 по­ка­за­на ил­лю­стра­ция к за­да­че. Изоб­ра­же­на си­ну­со­и­да, к точке кри­вой с абс­цис­сой  про­ве­де­на ка­са­тель­ная, ко­то­рая об­ра­зу­ет угол  с осью . Тан­генс дан­но­го угла необ­хо­ди­мо найти. Также необ­хо­ди­мо найти тан­генс угла, ко­то­рый об­ра­зо­вы­ва­ет­ся при пе­ре­се­че­нии оси абс­цисс с ка­са­тель­ной, про­ве­дён­ной к точке кри­вой с абс­цис­сой 0 и  .

Рис. 5. Ил­лю­стра­ция к за­да­че

Так как , то:

а) Для точки  тан­генс угла на­кло­на ка­са­тель­ной будет равен:

б) Для точки  тан­генс угла на­кло­на ка­са­тель­ной будет равен:

Сле­до­ва­тель­но, пря­мая , изоб­ра­жён­ная на ри­сун­ке 5, яв­ля­ет­ся ка­са­тель­ной к си­ну­со­и­де в точке 0.

в) Для точки , тан­генс угла на­кло­на ка­са­тель­ной будет равен:

Сле­до­ва­тель­но, в этом слу­чае ка­са­тель­ная па­рал­лель­на оси .

Ответ: а) ; б) ; в) .

ИСТОЧНИК

http://x-uni.com/algebra/10-klass/video/primery-vychisleniya-proizvodnyh-funktsiya-f-x-x-sup-3-sup-tipovye-zadachi

http://interneturok.ru/ru/school/algebra/10-klass/proizvodnaya/tablitsa-proizvodnyh-proizvodnye-trigonometricheskih-funktsiy-tipovye-zadachi

https://www.youtube.com/watch?v=fuCBw8gdRH8

http://11book.ru/images/shcoolbook_ru/10/10_a_mord_baz.pdf

http://www.absolom.ru/mathprofi/tipovye_zadachi_s_proizvodnoi.html

Таблица производных.

В мире — бесконечное множество функций. Среди этого множества есть функции, которые наиболее важны для практического применения. Эти функции сидят во всех законах природы. Из этих функций, как из кирпичиков, можно сконструировать все остальные. Этот класс функций называется элементарные функции. Именно эти функции и изучаются в школе — линейная, квадратичная, гипербола и т.п.

Дифференцирование функций «с нуля», т.е. исходя из определения производной и теории пределов — штука достаточно трудоёмкая. А математики — тоже люди, да-да!) Вот и упростили себе (и нам) жизнь. Они вычислили производные элементарных функций до нас. Получилась таблица производных, где всё уже готово.)

Вот она, эта табличка для самых популярных функций. Слева — элементарная функция, справа — её производная.

	Функция y	Производная функции y y’
1	C   (постоянная величина)	C’ = 0
2	x	x’ = 1
3	xn   (n — любое число)	(xn)’ = nxn-1
x2   (n = 2)	(x2)’ = 2x
4	sin x	(sin x)’ = cosx
cos x	(cos x)’ = — sin x
tg x
ctg x
5	arcsin x
arccos x
arctg x
arcctg x
4	ax
ex
5	loga x
ln x     (a = e)

Рекомендую обратить внимание на третью группу функций в этой таблице производных. Производная степенной функции — одна из самых употребительных формул, если только не самая употребительная! Намёк понятен?) Да, таблицу производных желательно знать наизусть

Кстати, это не так трудно, как может показаться. Попробуйте решать побольше примеров, таблица сама и запомнится!)

Найти табличное значение производной, как вы понимаете, задание не самое трудное. Поэтому очень часто в подобных заданиях встречаются дополнительные фишки. Либо в формулировке задания, либо в исходной функции, которой в таблице — вроде и нету…

Рассмотрим несколько примеров:

1. Найти производную функции y = x3

Такой функции в таблице нет. Но есть производная степенной функции в общем виде (третья группа). В нашем случае n=3. Вот и подставляем тройку вместо n и аккуратно записываем результат:

(x3)’ = 3·x3-1 = 3×2

Вот и все дела.

Ответ: y’ = 3×2

2. Найти значение производной функции y = sinx в точке х = 0.

Это задание означает, что надо сначала найти производную от синуса, а затем подставить значение х = 0 в эту самую производную. Именно в таком порядке! А то, бывает, сразу подставляют ноль в исходную функцию… Нас же просят найти не значение исходной функции, а значение её производной. Производная, напомню — это уже новая функция.

По табличке находим синус и соответствующую производную:

y’ = (sin x)’ = cosx

Подставляем ноль в производную:

y'(0) = cos 0 = 1

Это и будет ответ.

3. Продифференцировать функцию:

Что, внушает? ) Такой функции в таблице производных и близко нет.

Напомню, что продифференцировать функцию — это просто найти производную этой функции. Если забыть элементарную тригонометрию, искать производную нашей функции достаточно хлопотно. Таблица не помогает…

Но если увидеть, что наша функция — это косинус двойного угла, то всё сразу налаживается!

Да-да! Запомните, что преобразование исходной функции до дифференцирования вполне допускается! И, случается, здорово облегчает жизнь. По формуле косинуса двойного угла:

Т.е. наша хитрая функция есть не что иное, как y = cosx. А это — табличная функция. Сразу получаем:

Ответ: y’ = — sin x.

Пример для продвинутых выпускников и студентов:

4. Найти производную функции:

Такой функции в таблице производных нет, разумеется. Но если вспомнить элементарную математику, действия со степенями… То вполне можно упростить эту функцию. Вот так:

А икс в степени одна десятая — это уже табличная функция! Третья группа, n=1/10. Прямо по формуле и записываем:

Вот и всё. Это будет ответ.

Надеюсь, что с первым китом дифференцирования — таблицей производных — всё ясно. Осталось разобраться с двумя оставшимися китами. В следующем уроке освоим правила дифференцирования.

Производные основных элементарных функций

Теперь мы найдем производные всех основных элементарных функций; начнем с постоянной функции.

Производные основных элементарных функций

Теперь найдем производные всех основных элементарных функций; начнем с постоянной функции.

(1) Производная постоянной функции равна нулю.

Пусть y = f(x) = k, k — константа.

Тогда f(x + ∆x) = k и

f(x + ∆x) — f(x) = k — k = 0.

(2) Степенная функция y = xn, n > 0 является целым числом.

Пусть f(x) = xn.

Тогда f(x + ∆x) = (x + ∆x)n и

f(x + ∆x) — f(x) = (x + ∆x)n — xn.

(3) Производная логарифмической функции

Натуральный логарифм x обозначается loge x или logx или ln x

x) = log (x + ∆x) и

f(x + ∆x) — f(x) = log (x + ∆x) — log x

(4) Производная показательной функции

Пусть y = ax

Тогда f (x + ∆x) — f (x) = ax + ∆x− ax

= ax (a ∆x−1) и

(5) Производные тригонометрических функций

(i) Функция синуса sinx.

Пусть y = f (x) = sin x.

Тогда f (x + ∆x) = sin(x + ∆x) и

(ii) функция косинуса, cos x

(iii) функция тангенса, tan x

Пусть y = f (x) = tan x .

(iv) Функция Secant, Sec x

(v) Функция Cosecant, Cosec X

(VI) Функция COTANGENT, Cot X

1310 (VI). Производные обратных тригонометрических функций

(i) Производная arcsin x или sin−1 x

Пусть y= f (x) = sin−1 x .

Тогда  y + ∆y= f (x + ∆x) = sin−1 (x +  ∆x)

Отсюда следует, что x= sin y и

х + ∆x= sin (y + ∆y).

(ii) Производная arccos x или cos-1x

Мы знаем тождество:

(iii) Производная arctan x или tan-1 x

x Пусть y = f ( ) = тангенс −1 х .

Отсюда следует, что y + ∆y= f(x + ∆x) = tan−1 (x + ∆x)          … (2)

x= tan y и

x+ ∆ x = tan (y + ∆y)

Отсюда следует, что ∆x = tan (y + ∆y) — tan y

(iv) Производная arccot ​​x или cot−1 x

(v) Производная arcsec x or

(vi) Производная arccosec x or

5 Доказательства

5 (v) и (vi) оставлены в качестве упражнений.

УПРАЖНЕНИЕ 10.2

Найдите производные следующих функций по соответствующим независимым переменным:

(1) f(x) = x — 3 sinx

(2) y = sin x + cos x

(3) f(x) = x sin x

(4) y = cos x — 2 tan x

(5) g(t) = t3cos t

(6) g(t) = 4 с t + tg t

(7) y = ex sin x

(8) y = tanx /x

(9) y = sin x /

(10) y = x /

(11) y = tan x −1 / сек x

(12) y = sin x / x2

(13) y = tan θ(sin θ + cos θ)

( 14) у = косек х .

Формулы дифференцирования в высшей математике

С помощью таблицы производных решают разнообразные прикладные задания в алгебре. Производная обозначает скорость изменения какой-либо величины. К примеру, если рассмотреть производную у(х) по х, можно определить, с какой скоростью изменяются координаты у по мере изменения координаты х. Если взять производную от скорости, с которой меняется координата у относительно координаты х, то достаточно просто рассчитать ускорение.

Применение производной в задачах по физике позволяет определить производную пути S по времени, то есть скорость. Это связано с тем, что скорость является величиной, характеризующей быстроту изменения расстояния относительно времени. Производная скорости представляет собой ускорение, которое характеризует быстроту изменения скорости.

Заметим, что наличие множества различных функций усложняет процесс дифференцирования. Гораздо проще функцию, записанную из разных элементарных функций, дифференцировать с помощью готовых выражений для производных данных элементарных функций.

При работе с производными удобно пользоваться специальной таблицей. В ней указаны производные простейших функций. В результате получится вычислить производную от любой функции. При этом полезно овладеть навыками дифференцирования. Задача упрощается, благодаря ряду правил дифференцирования.

Дифференцирование подразумевает определение производных и дифференциалов какого-либо порядка от функции одной переменной, частных производных, дифференциалов, полных дифференциалов от функций многих переменных.

Слайд 10 Василий Иванович Висковатов (26 декабря 1779 (6 января

1780), Санкт-Петербург — 8 (20) октября 1812, Санкт-Петербург) —

русский математик. Известный
специалист в области математического анализа и вариационного

исчисления, один из активных последователей С. Г. Гурьева в пропаганде новых передовых научных идей.

Выпущен из Артиллерийского и Инженерного Шляхетского Кадетского Корпуса в 1796 года штык-юнкером в корпусные офицеры.
С 1803 года признан крупным математиком, избран академиком Петербургской Академии наук.
С 1810 года — профессор чистой и прикладной математики в Институте Корпуса инженеров путей сообщения.
Впервые употребил русский термин «производная функции».

Назад

Слайд 18 Далее, подставляем уже известные выражения производных числителя и

знаменателя и упрощаем выражение полученной производной:

·[1/(x2)2]=[(1/2√x)·x2-(√x)·2x]·[1/(x2)2]=[(1/2x½)·x2-(x½)·2x]·[1/(x2)2]=·[1/x4]=[½·x3/2-2·x3/2]·[1/x4]=-[(3/2)·x3/2]·[1/x4]=-(3/2)·x-5/2

Здесь мы воспользовались тем,

что корень квадратный есть степень с показателем (1/2), при умножении

степеней их показатели складываются, при делении степеней – показатели вычитаются, а при возведении степени в степень показатели перемножаются. Также при делении разности на некоторый знаменатель каждый член этой разности делится на знаменатель и берется их разность.

назад

Правила дифференцирования сложных функций

Конечно, далеко не все функции выглядят так, как в вышеуказанной таблице. Как быть с дифференцированием, например, вот таких функций: y = (3 + 2×2)4?

Сложной функцией называют такое выражение, в котором одна функция словно вложена в другую. Производную сложной функции f(y) можно найти по следующей формуле: (f(y))′ = f′(y) ⋅ y′. Другими словами, нужно умножить производную, условно говоря, внешней функции на производную внутренней.

Пример 1

Найдем производную функции y(x) = (3 + 2×2)4.

Заменим 3 + 2×2 на u и тогда получим y = u4.

Согласно приведенному выше правилу дифференцирования сложных функций у нас получится:

y = y′_u ⋅ u′_x = 4u3 ⋅ u’_x

А теперь выполним обратную замену и подставим исходное выражение:

4u3 ⋅ u′_x = 4 (3 + 2×2)3 ⋅ (3 + 2×2)′ = 16 (3 + 2×2)3 ⋅ х

Пример 2

Найдем производную для функции y = (x3 + 4) cos x.

Для дифференцирования этой функции воспользуемся формулой (UV)′ = U′V + V′U.

y′ = (x3 + 4)′ ⋅ cos x + (x3 + 4) ⋅ cos x′ = 3×2 ⋅ cos x + (x3 + 4) ⋅ (-sin x) = 3×2 ⋅ cos x – (x3 + 4) ⋅ sin x

Производная произведения

Математика — наука логичная, поэтому многие считают, что если производная суммы равна сумме производных, то производная произведения strike

«>равна произведению производных. А вот фиг вам! Производная произведения считается совсем по другой формуле. А именно:

(f

· g

) ’ = f

’ · g

+ f

· g

’

Формула несложная, но ее часто забывают. И не только школьники, но и студенты. Результат — неправильно решенные задачи.

Функция f

(x

) представляет собой произведение двух элементарных функций, поэтому все просто:

f

’(x

) = (x

3 · cos x

)’ = (x

3)’ · cos x

+ x

3 · (cos x

)’ = 3x

2 · cos x

+ x

3 · (− sin x

) = x

2 · (3cos x

− x

· sin x

)

У функции g

(x

) первый множитель чуть посложней, но общая схема от этого не меняется. Очевидно, первый множитель функции g

(x

) представляет собой многочлен, и его производная — это производная суммы. Имеем:

g

’(x

) = ((x

2 + 7x

− 7) · e

x

)’ = (x

2 + 7x

− 7)’ · e

x

+ (x

2 + 7x

− 7) · (e

x

)’ = (2x

+ 7) · e

x

+ (x

2 + 7x

− 7) · e

x

= e

x

· (2x

+ 7 + x

2 + 7x

−7) = (x

2 + 9x

) · e

x

= x

(x

+ 9) · e

x

.

Ответ:f

’(x

) = x

2 · (3cos x

− x

· sin x

);g

’(x

) = x

(x

+ 9) · e

x

.

Обратите внимание, что на последнем шаге производная раскладывается на множители. Формально этого делать не нужно, однако большинство производных вычисляются не сами по себе, а чтобы исследовать функцию

А значит, дальше производная будет приравниваться к нулю, будут выясняться ее знаки и так далее. Для такого дела лучше иметь выражение, разложенное на множители.

Если есть две функции f

(x

) и g

(x

), причем g

(x

) ≠ 0 на интересующем нас множестве, можно определить новую функцию h

(x

) = f

(x

)/g

(x

). Для такой функции тоже можно найти производную:

Неслабо, да? Откуда взялся минус? Почему g

2 ? А вот так! Это одна из самых сложных формул — без бутылки не разберешься. Поэтому лучше изучать ее на конкретных примерах.

В числителе и знаменателе каждой дроби стоят элементарные функции, поэтому все, что нам нужно — это формула производной частного:

По традиции, разложим числитель на множители — это значительно упростит ответ:

Сложная функция — это не обязательно формула длиной в полкилометра. Например, достаточно взять функцию f

(x

) = sin x

и заменить переменную x

, скажем, на x

2 + ln x

. Получится f

(x

) = sin (x

2 + ln x

) — это и есть сложная функция. У нее тоже есть производная, однако найти ее по правилам, рассмотренным выше, не получится.

Как быть? В таких случаях помогает замена переменной и формула производной сложной функции:

f

’(x

) = f

’(t

) · t

’, если x

заменяется на t

(x

).

Как правило, с пониманием этой формулы дело обстоит еще более печально, чем с производной частного. Поэтому ее тоже лучше объяснить на конкретных примерах, с подробным описанием каждого шага.

Заметим, что если в функции f

(x

) вместо выражения 2x

+ 3 будет просто x

, то получится элементарная функция f

(x

) = e

x

. Поэтому делаем замену: пусть 2x

+ 3 = t

, f

(x

) = f

(t

) = e

t

. Ищем производную сложной функции по формуле:

f

’(x

) = f

’(t

) · t

’ = (e

t

)’ · t

’ = e

t

· t

’

А теперь — внимание! Выполняем обратную замену: t

= 2x

+ 3. Получим:

f

’(x

) = e

t

· t

’ = e

2x

+ 3 · (2x

+ 3)’ = e

2x

+ 3 · 2 = 2 · e

2x

+ 3

Теперь разберемся с функцией g

(x

). Очевидно, надо заменить x

2 + ln x

= t

. Имеем:

g

’(x

) = g

’(t

) · t

’ = (sin t

)’ · t

’ = cos t

· t

’

Обратная замена: t

= x

2 + ln x

. Тогда:

g

’(x

) = cos (x

2 + ln x

) · (x

2 + ln x

)’ = cos (x

2 + ln x

) · (2x

+ 1/x

).

Вот и все! Как видно из последнего выражения, вся задача свелась к вычислению производной суммы.

Ответ:f

’(x

) = 2 · e

2x

+ 3 ;g

’(x

) = (2x

+ 1/x

) · cos (x

2 + ln x

).

Очень часто на своих уроках вместо термина «производная» я использую слово «штрих». Например, штрих от суммы равен сумме штрихов. Так понятнее? Ну, вот и хорошо.

Таким образом, вычисление производной сводится к избавлению от этих самых штрихов по правилам, рассмотренным выше. В качестве последнего примера вернемся к производной степени с рациональным показателем:

(x

n

)’ = n

· x

n

− 1

Немногие знают, что в роли n

вполне может выступать дробное число. Например, корень — это x

0,5 . А что, если под корнем будет стоять что-нибудь навороченное? Снова получится сложная функция — такие конструкции любят давать на контрольных работах и экзаменах.

Для начала перепишем корень в виде степени с рациональным показателем:

f

(x

) = (x

2 + 8x

− 7) 0,5 .

Теперь делаем замену: пусть x

2 + 8x

− 7 = t

. Находим производную по формуле:

f

’(x

) = f

’(t

) · t

’ = (t

0,5)’ · t

’ = 0,5 · t

−0,5 · t

’.

Делаем обратную замену: t

= x

2 + 8x

− 7. Имеем:

f

’(x

) = 0,5 · (x

2 + 8x

− 7) −0,5 · (x

2 + 8x

− 7)’ = 0,5 · (2x

+ · (x

2 + 8x

− 7) −0,5 .

Наконец, возвращаемся к корням:

Приводится доказательство формулы производной сложной функции. Подробно рассмотрены случаи, когда сложная функция зависит от одной и двух переменных. Производится обобщение на случай произвольного числа переменных.

Здесь мы приводим вывод следующих формул для производной сложной функции. Если ,
то.
Если ,
то.
Если ,
то.

Слайд 41 В11 Найдите точку максимума функции Задачи для дополнительного

решенияНайдите точку минимума функции Решение: Найдём производную данной функции

и найдем критические точки, для этого решим уравнение Д= 49 + 240 = 289х= — 4 , х = При переходе через точку -4 производная меняет знак с «+» на «-»,Значит х = -4 является точкой максимума. Ответ: -4

Вывод 3В решениях заданий, встречаемых в сборниках по подготовке к ЕГЭ по математике применяются формулы и правила нахождения производной, геометрический и механический смысл производной, понятие критической точки, признаки возрастания и убывания функцииметоды нахождения наибольшего и наименьшего значений функции, точек максимума и минимума.Для успешной сдачи ЕГЭ по математике необходимо прорешать большой объём заданий различного уровня сложности.

Производная функции — краткое описание, суть

Если совсем просто, то:

Производная – это скорость изменения функции в данной точке.

Выражаясь математическим языком, это предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю. Формула:

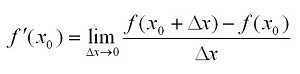
Она понимается в двух смыслах: геометрическом и физическом.

Геометрический смысл: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

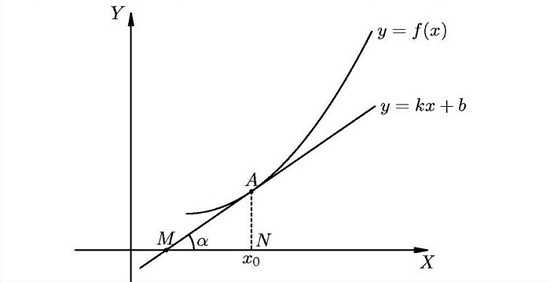
Физический смысл: производная пути по времени равна скорости прямолинейного движения. Таким образом, значение скорости в определённый момент времени t определяется по формуле:

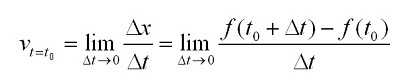
Вычисление производной называется дифференцированием. Обратный процесс – интегрированием.

Вывод простейших для нахождения производных конкретных функций

При решении задач с элементарными и сложными функциями удобно пользоваться нижеприведенными основными формулами для нахождения их производной.

1. Производная натурального логарифма по x для элементарной функции имеет общий вид .

В случае расчетов со сложными функциями следует воспользоваться формулой .

2. Производная логарифмической функции по основанию a для элементарной функции вычисляется таким образом: 

Если функция сложная, то формула примет следующий вид: 

3. Производная по x в степени n определяется, согласно краткому уравнению .

Когда в решении задачи присутствует сложная функция, можно воспользоваться формулой: 

4. Производная квадратного корня для элементарной функции равна: .

Для сложной функции: .

5. При расчете производной a в степени x нужно использовать формулу , когда функция элементарная.

Используем формулу , когда функция сложная.

6. Производная e в степени x в случае элементарной функции составляет .

Если функция сложная, то формула примет вид: .

7. Производная синуса для элементарной функции равна .

В случае сложной функции значение можно посчитать так: .

8. Производная косинуса для элементарной функции 

Для сложной функции — 

9. Когда требуется определить производную тангенса для элементарной функции, следует воспользоваться формулой: 

Если функция сложная, то подойдет следующая формула: 

10. Вычислить производную котангенса для элементарной функции можно с помощью уравнения .

Для сложной функции — .

11. Формула производной арксинуса имеет вид: 

Если функция сложная, то следует воспользоваться следующей формулой: .

12. Производную арккосинуса для элементарной функции вычисляют таким образом: .

В случае сложной функции формула следующая: .

13. Если требуется вычислить производную арктангенса для элементарной функции, пригодится формула: .

В случае сложной функции следует использовать такую формулу: .

14. Производная арккотангенса для элементарной функции: .

Для сложной функции производную вычисляют следующим образом: .