Способы нахождения площади кругового сектора

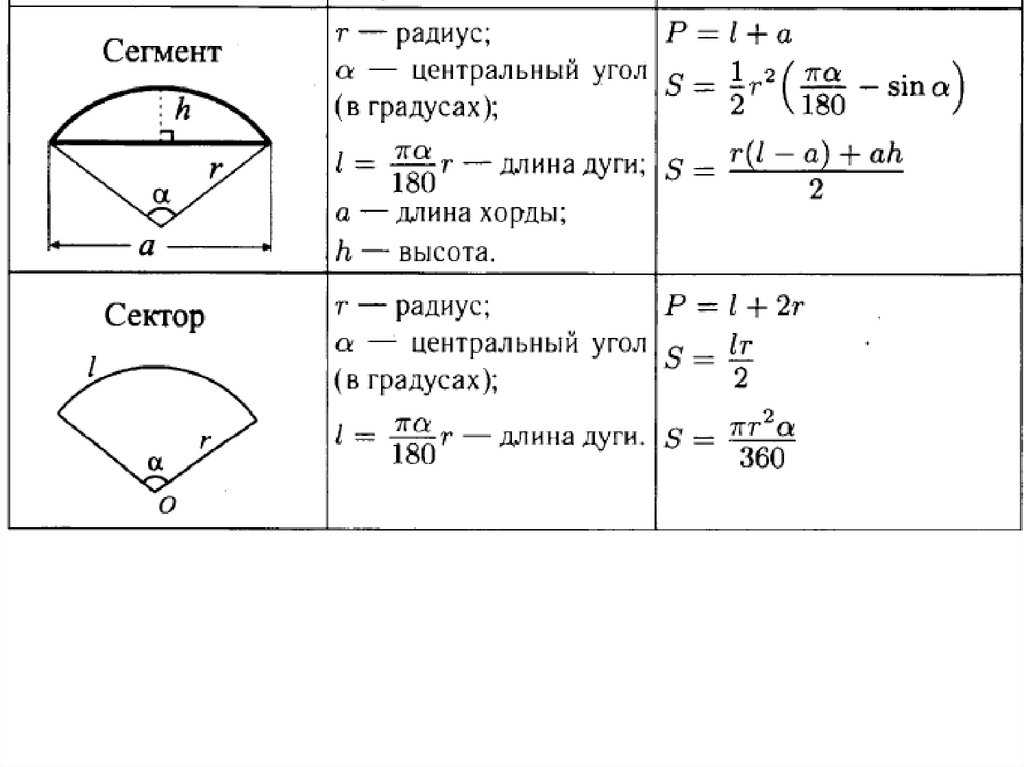
Площадь круга

      Рассмотрим две окружности с общим центром (концентрические окружности) и радиусами радиусами 1 и R, в каждую из которых вписан правильный   n – угольник (рис. 1).

      Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1.

Рис.1

      Площадь правильного n – угольника, вписанного в окружность радиуса R, равна

      Площадь правильного n – угольника, вписанного в окружность радиуса 1, равна

      Следовательно,

      Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1, стремится к π, то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R, стремится к числу   πR2.

      Таким образом, площадь круга радиуса R, обозначаемая S, равна

S = πR2.

Уравнение круга в стандартной форме

Если центр окружности расположен в начале координат, мы можем взять любую точку окружности и наложить прямоугольный треугольник с гипотенузой, соединяющей эту точку с центром.

Тогда, согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов на двух других сторонах. Если радиус окружности равен r, то это гипотенуза прямоугольного треугольника, поэтому мы можем записать уравнение в виде:

х 2 + у 2 = г 2

Это уравнение окружности в стандартной форме в декартовых координатах.

Если окружность центрируется в точке (a, b), уравнение окружности будет следующим:

( х — а ) 2 + ( у — б ) 2 = г 2

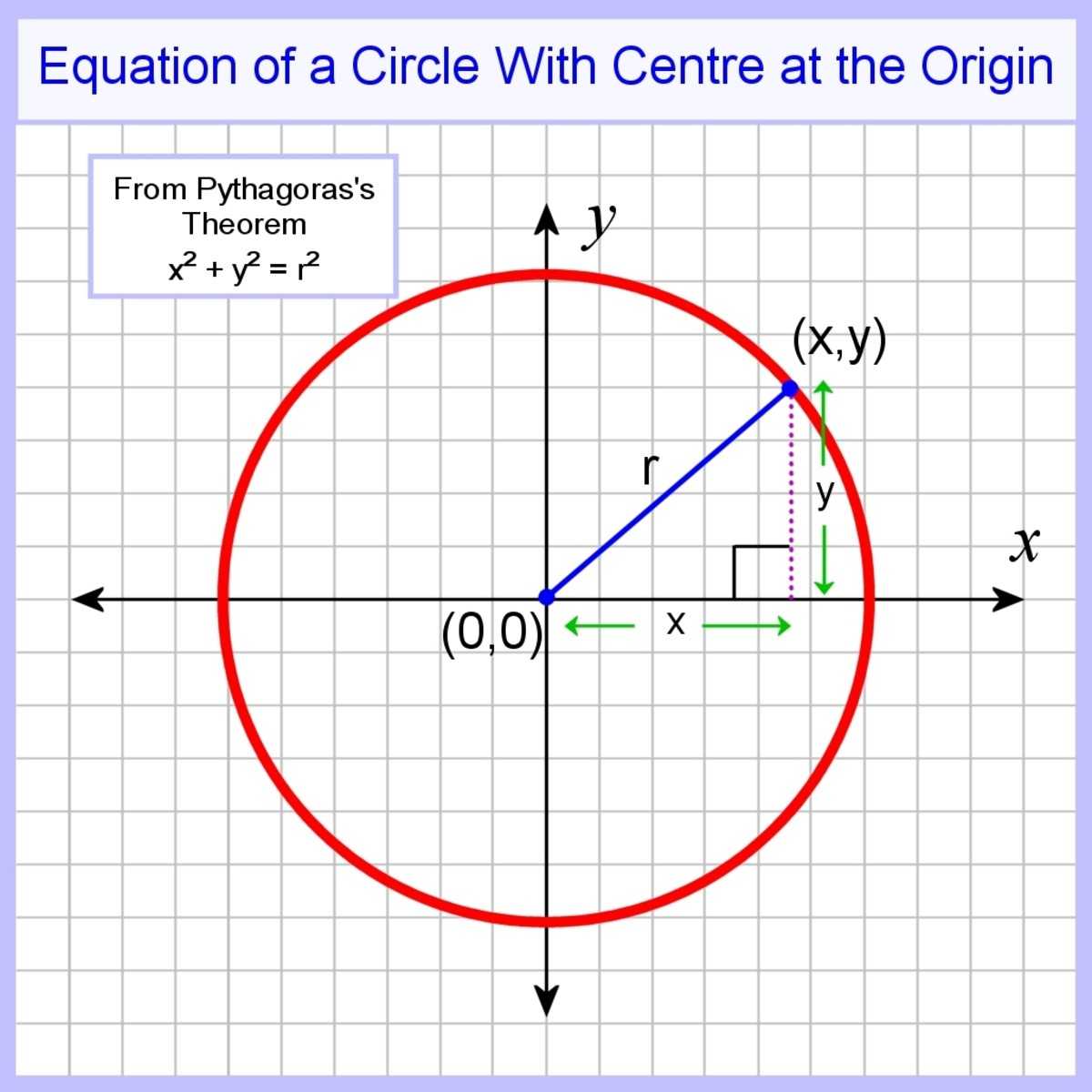
Уравнение круга с центром в начале координат: r² = x² + y².

Изображение Юджин Бреннан

Формула площади сегмента круга через радиус и длину дуги круга, высоту и основание треугольника

S = 1 2 ⋅ R ⋅ s − 1 2 ⋅ h ⋅ a S=\frac{1}{2}\cdot R\cdot s-\frac{1}{2}\cdot h\cdot a
S
=

2

1

​

⋅

R
⋅

s
−

2

1

​

⋅

h
⋅

a

R R
R

— радиус круга; s s
s

— длина дуги; h h
h

— высота равнобедренного треугольника; a a
a

— длина основания этого треугольника.

Дан круг, его радиус, численно равный 5 (см.), высота, которая проведена к основанию треугольника, равная 2 (см.), длина дуги 10 (см.). Найти площадь сегмента круга.

Решение

R = 5 R=5
R
=

5

h = 2 h=2
h
=

2

s = 10 s=10
s
=

1
0

Для вычисления площади нам не хватает только основания треугольника. Найдем его по формуле:

A = 2 ⋅ h ⋅ (2 ⋅ R − h) = 2 ⋅ 2 ⋅ (2 ⋅ 5 − 2) = 8 a=2\cdot\sqrt{h\cdot(2\cdot R-h)}=2\cdot\sqrt{2\cdot(2\cdot 5-2)}=8
a
=

2
⋅

h
⋅
(2
⋅
R
−
h
)

​

=

2
⋅

2
⋅
(2
⋅
5
−
2
)

​

=

8

Теперь можно вычислить площадь сегмента:

S = 1 2 ⋅ R ⋅ s − 1 2 ⋅ h ⋅ a = 1 2 ⋅ 5 ⋅ 10 − 1 2 ⋅ 2 ⋅ 8 = 17 S=\frac{1}{2}\cdot R\cdot s-\frac{1}{2}\cdot h\cdot a=\frac{1}{2}\cdot 5\cdot 10-\frac{1}{2}\cdot 2\cdot 8=17
S
=

2

1

​

⋅

R
⋅

s
−

2

1

​

⋅

h
⋅

a
=

2

1

​

⋅

5
⋅

1
0
−

2

1

​

⋅

2
⋅

8
=

1
7

(см. кв.)

Ответ:
17 см. кв.

Длина окружности (периметр круга)

Будем выводить длину произвольной окружности \(C \)
с помощью её радиуса, равного \(τ \)
.

Будем рассматривать две произвольные окружности. Обозначим их длины через \(C \)
и \(C» \)
, у которых радиусы равняются \(τ \)
и \(τ» \)
. Будем вписывать в эти окружности правильные \(n \)
-угольники, периметры которых равняются \(ρ \)
и \(ρ» \)
, длины сторон которых равняются \(α \)
и \(α» \)
, соответственно. Как мы знаем, сторона вписанного в окружность правильного \(n \)
– угольника равняется

\(α=2τsin\frac{180^0}{n} \)

Тогда, будем получать, что

\(ρ=nα=2nτ\frac{sin180^0}{n} \)

\(ρ»=nα»=2nτ»\frac{sin180^0}{n} \)

\(\frac{ρ}{ρ»}=\frac{2nτsin\frac{180^0}{n}}{2nτ»\frac{sin180^0}{n}}=\frac{2τ}{2τ»} \)

Получаем, что отношение \(\frac{ρ}{ρ»}=\frac{2τ}{2τ»} \)
будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть

\(\lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{2τ}{2τ»} \)

С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть \(n→∞ \)
), будем получать равенство:

\(lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{C}{C»} \)

Из последних двух равенств получим, что

\(\frac{C}{C»}=\frac{2τ}{2τ»} \)

\(\frac{C}{2τ}=\frac{C»}{2τ»} \)

Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть

\(\frac{C}{2τ}=const \)

Эту постоянную принять называть числом «пи» и обозначать \(π \)
. Приближенно, это число будет равняться \(3,14 \)
(точного значения этого числа нет, так как оно является иррациональным числом). Таким образом

\(\frac{C}{2τ}=π \)

Окончательно, получим, что длина окружности (периметр круга) определяется формулой

\(C=2πτ \)

В вашем браузере отключен Javascript. Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.

Узнать длину окружности

Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.

Рассчитать площадь шара

Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.

Вычислить объем шара

Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы
, понятия и определения требуются для этого.

формулы через радиус и угол сектора

В данной публикации мы рассмотрим определение сегмента круга и формулы, с помощью которых можно вычислить его площадь (через радиус и центральный угол кругового сектора).

Определение сегмента круга

Сегмент круга – это часть круга, которая ограничена дугой окружности и ее хордой.

Хорда – это часть прямой (секущей), которая пересекает круг. Концы хорды соединяются с центром круга, в результате чего образуется равнобедренный треугольник, боковые стороны которого являются радиусом окружности. Если к этом треугольнику добавить сегмент, получится сектор.

На рисунке выше:

• сегмент круга закрашен зеленым цветом;
• отрезок AB – это хорда;
• часть окружности между точками AB – дуга окружности;
• R – радиус круга;
• α – угол сектора.

Формулы нахождения площади кругового сегмента

α° – угол в градусах.

Примечание: в расчетах используется значение π, приблизительное равное числу 3,14.

Через радиус и угол сектора в радианах

α_рад – угол в радианах.

Примеры задачи

Задание 1Найдите площадь сегмента круга, если его радиус равен 8 см, а центральный угол сектора, стягивающего сегмент, составляет 45 градусов.

РешениеВоспользуемся первой формулой, подставив в нее известные значения:

Задание 2Площадь кругового сегмента составляет 24 см2, а центральный угол сектора круга, частью которого является сегмент, равняется 1 радиану. Найдите радиус круга.

РешениеВ данном случае мы можем получить радиус из формулы, в которой задействован угол в радианах:

Площадь круга и его частей. Длина окружности и ее дуг

Справочник по математике

Геометрия (Планиметрия)

Окружность и круг

Фигура	Рисунок	Определения и свойства
Окружность	Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Дуга	Часть окружности, расположенная между двумя точками окружности
Круг	Конечная часть плоскости, ограниченная окружностью
Сектор	Часть круга, ограниченная двумя радиусами
Сегмент	Часть круга, ограниченная хордой
Правильный многоугольник	Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности

Дуга

Часть окружности, расположенная между двумя точками окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Сектор

Часть круга, ограниченная двумя радиусами

Сегмент

Часть круга, ограниченная хордой

Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны Около любого правильного многоугольника можно описать окружность

      Определение 1. Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.

      Определение 2. Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.

      Замечание 1. Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.

      Определение 3. Числом π (пи) называют число, равное площади круга радиуса 1.

      Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.

Площадь круга

      Рассмотрим две окружности с общим центром (концентрические окружности) и радиусами радиусами 1 и R, в каждую из которых вписан правильный   n – угольник (рис. 1).

      Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1.

Рис.1

      Площадь правильного n – угольника, вписанного в окружность радиуса R, равна

      Площадь правильного n – угольника, вписанного в окружность радиуса 1, равна

      Следовательно,

      Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1, стремится к π, то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R, стремится к числу   πR2.

      Таким образом, площадь круга радиуса R, обозначаемая S, равна

S = πR2.

Длина окружности

      Рассмотрим правильный   n – угольник   B1B2…Bn , вписанный в окружность радиуса радиуса R, и опустим из центраO окружности перпендикуляры на все стороны многоугольника (рис. 2).

Рис.2

      Поскольку площадь n – угольника   B1B2…Bn   равна

то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство:

откуда вытекает формула для длины окружности радиуса R:

C = 2πR.

      Следствие. Длина окружности радиуса 1 равна   2π.

Длина дуги

      Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

Рис.3

      В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

      В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сектора

      Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.

Рис.4

      В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

      В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сегмента

      Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

Рис.5

      Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем

      Следовательно,

      В случае, когда величина α выражена в в радианах, получаем

      Следовательно,

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Формулы площади сектора круга и длины его дуги

Окружность — основная фигура в геометрии, свойства которой рассматривают в школе в 8 классе. Одна из типичных задач, связанных с окружностью, заключается в нахождении площади некоторой ее части, которая носит название кругового сектора. В статье приводятся формулы площади сектора и длины его дуги, а также пример их использования для решения конкретной задачи.

Понятие об окружности и круге

Перед тем как приводить формулу площади сектора окружности, рассмотрим, что собой представляет указанная фигура. Согласно математическому определению, под окружностью понимают такую фигуру на плоскости, все точки которой равноудалены от некоторой одной точки (центра).

Когда рассматривают окружность, то пользуются следующей терминологией:

• Радиус — отрезок, который проводится от центральной точки до кривой окружности. Его принято обозначать буквой R.
• Диаметр — это отрезок, который соединяет две точки окружности, но при этом проходит также через центр фигуры. Его обычно обозначают буквой D.
• Дуга — это часть кривой окружности. Измеряют ее либо в единицах длины, либо с использованием углов.

Круг — еще одна важная фигура геометрии, он представляет собой совокупность точек, которая ограничена кривой окружности.

Площадь круга и длина окружности

Отмеченные в названии пункта величины рассчитываются с использованием двух простых формул. Они приведены ниже:

• Длина окружности: L = 2*pi*R.
• Площадь круга: S = pi*R2.

В этих формулах pi — это некоторая константа, которая называется числом Пи. Оно является иррациональным, то есть не может быть точно выражено простой дробью. Приблизительно число Пи равно 3,1416.

Как видно из приведенных выражений, чтобы рассчитать площадь и длину достаточно знать только радиус окружности.

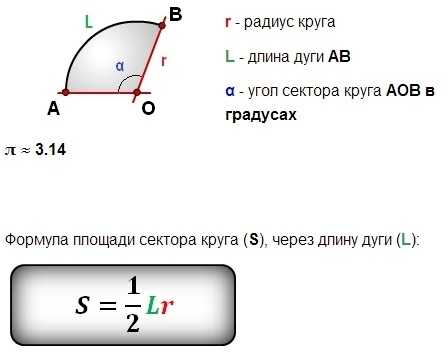
Площадь сектора круга и длина его дуги

Перед тем как рассматривать соответствующие формулы, напомним, что угол в геометрии принято выражать двумя основными способами:

• в шестидесятеричных градусах, причем полный оборот вокруг своей оси равен 360o;
• в радианах, которые выражаются в долях числа pi и связаны с градусами следующим равенством: 2*pi = 360o.

Сектор круга — это фигура, ограниченная тремя линиями: дугой окружности и двумя радиусами, находящимися на концах этой дуги. Пример кругового сектора изображен на фото ниже.

Получив представление о том, что такое сектор для круга, легко понять, как вычислить его площадь и длину соответствующей дуги. Из рисунка выше видно, что дуге сектора соответствует угол θ. Мы знаем, что полная окружность соответствует 2*pi радианам, значит, формула площади кругового сектора примет вид: S₁ = S*θ/(2*pi) = pi*R2*θ/(2*pi) = θ*R2/2. Здесь угол θ выражен в радианах. Аналогичная формула площади сектора в случае, если угол θ измеряется в градусах, будет иметь вид: S₁ = pi*θ*R2/360.

Длина дуги, образующей сектор, вычисляется по формуле: L₁ = θ*2*pi*R/(2*pi) = θ*R. И если θ известен в градусах, тогда: L₁ = pi*θ*R/180.

Пример решения задачи

Покажем на примере простой задачи, как пользоваться формулами площади сектора круга и длины его дуги.

Известно, что колесо имеет 12 спиц. Когда колесо делает один полный оборот, то оно преодолевает расстояние 1,5 метра. Чему равна площадь, заключенная между двумя соседними спицами колеса, и чему равна длина дуги между ними?

Как видно из соответствующих формул, чтобы ими пользоваться, необходимо знать две величины: радиус окружности и угол дуги. Радиус можно вычислить, исходя из знания длины окружности колеса, поскольку пройденное им расстояние за один оборот, точно ей соответствует. Имеем: 2*R*pi = 1,5, откуда: R = 1,5/(2*pi) = 0,2387 метра. Угол между ближайшими спицами можно определить, зная их число. Полагая, что все 12 спиц делят равномерно круг на равные сектора, мы получаем 12 одинаковых секторов. Соответственно, угловая мера дуги между двумя спицами равна: θ = 2*pi/12 = pi/6 = 0,5236 радиан.

Мы нашли все необходимые величины, теперь их можно подставить в формулы и посчитать требуемые условием задачи значения. Получаем: S₁ = 0,5236*(0,2387)2/2 = 0,0149 м2, или 149 см2; L₁ = 0,5236*0,2387 = 0,125 м, или 12,5 см.

Геометрия круга

7.07.2012 // Владимир Трунов   

Круг, его части, их размеры и соотношения — вещи, с которыми ювелир постоянно сталкивается. Кольца, браслеты, касты, трубки, шары, спирали — много всего круглого приходится делать. Как же всё это посчитать, особенно если тебе посчастливилось в школе прогулять уроки геометрии?..

Давайте сначала рассмотрим, какие у круга бывают части и как они называются.

• Окружность — линия, ограничивающая круг.
• Дуга — часть окружности.
• Радиус — отрезок, соединяющий центр круга с какой-либо точкой окружности.
• Хорда — отрезок, соединяющий две точки окружности.
• Сегмент — часть круга, ограниченная хордой и дугой.
• Сектор — часть круга, ограниченная двумя радиусами и дугой.

Интересующие нас величины и их обозначения:

• R — радиус круга (здесь «радиус» — это уже не отрезок, а его длина);
• D — диаметр круга — двойной радиус;
• C — длина окружности;
• L — длина дуги;
• X — длина хорды;
• H — высота сегмента;
• φ — центральный угол — угол между двумя радиусами;
• — площадь круга;
• — площадь сектора;
• — площадь сегмента.

Теперь посмотрим, какие задачи, связанные с частями круга, приходится решать.

• Найти длину развертки какой-либо части кольца (браслета). Задан диаметр и хорда (вариант: диаметр и центральный угол), найти длину дуги.
• Есть рисунок на плоскости, надо узнать его размер в проекции после сгибания в дугу. Заданы длина дуги и диаметр, найти длину хорды.
• Узнать высоту детали, полученной сгибанием плоской заготовки в дугу. Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента.

Жизнь подскажет и другие примеры, а эти я привел только для того, чтобы показать необходимость задания каких-нибудь двух параметров для нахождения всех остальных. Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.

Чтобы зря не грузить читателя, подробных решений я приводить не буду, а приведу лишь результаты в виде формул (те случаи, где нет формального решения, я оговорю по ходу дела).

И еще одно замечание: о единицах измерения. Все величины, кроме центрального угла, измеряются в одних и тех же абстрактных единицах.

И только центральный угол во всех случаях измеряется в градусах и ни в чём другом. Потому что, как показывает практика, люди, проектирующие что-нибудь круглое, не склонны измерять углы в радианах.

Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α.

По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.

2. Даны диаметр D и длина хорды X

;     длина дуги ;высота сегмента ;    центральный угол .

Поскольку хорда делит круг на два сегмента, у этой задачи не одно, а два решения. Чтобы получить второе, нужно в приведенных выше формулах заменить угол α на угол .

10. Даны центральный угол φ и высота сегмента H

;     диаметр ;длина дуги ;    длина хорды .

Внимательный читатель не мог не заметить, что я пропустил два варианта:

7. Даны длина дуги L и высота сегмента H

Это как раз те два неприятных случая, когда у задачи нет решения, которое можно было бы записать в виде формулы. А задача-то не такая уж редкая. Например, у вас есть плоская заготовка длины L, и вы хотите согнуть ее так, чтобы ее длина стала X (или высота стала H). Какого диаметра взять оправку (ригель)?

Задача эта сводится к решению уравнений:; — в варианте 5; — в варианте 7и хоть они и не решаются аналитически, зато легко решаются программным способом. И я даже знаю, где взять такую программу: на этом самом сайте, под именем Segment. Всё то, что я тут длинно рассказываю, она делает за микросекунды.

Для полноты картины добавим к результатам наших вычислений длину окружности и три значения площадей — круга, сектора и сегмента. (Площади нам очень помогут при вычислении массы всяких круглых и полукруглых деталей, но об этом — в отдельной статье.) Все эти величины вычисляются по одним и тем же формулам:

длина окружности ;площадь круга ;площадь сектора ;площадь сегмента ;

Программа Segment

Программа вычисления параметров сегмента круга

Программа Segment предназначена для вычисления геометрических параметров сегмента круга. В расчетах участвуют пять величин:

• диаметр круга,
• длина дуги,
• длина хорды,
• центральный угол,
• высота сегмента,

любые две из которых задаются, а оставшиеся вычисляются.

Дополнительно вычисляются значения:

• длины окружности,
• площади круга,
• площади сегмента,
• площади сектора,

соответствующие заданным величинам.

Теоретическая сторона вычислений описана в статье Геометрия круга.

Программа очень пригодится людям, проектирующим что-нибудь круглое. Например, ювелирам для разработки эскизов колец, браслетов и прочей ерунды.

Segment рассчитана на выполнение под Windows (XP, 7, 8, 10) и не требует специальной установки. Нужно просто извлечь из архива два файла и поместить их в одну папку.

• Segment.exe — выполняемый файл;
• SegmentHelp.chm — файл справки, который открывается не только из программы, но и отдельно, так что вы можете изучить его еще до запуска программы.

Для удаления программы — просто удалить эти файлы.

Программа распространяется бесплатно и не содержит рекламы.

Примечание 1. Если у программы возникнут проблемы с системой безопасности Windows, то обратитесь к статье Как скачать программу.

Примечание 2. Если при запуске программы вы получаете сообщение, содержащее название .NET Framework, то обратитесь к статье Что такое .NET Framework.

Примечание 3. Если вы скачали программу, то настоятельно советую вам подписаться на рассылку «Новости сайта tvlad.ru» (форма в правой колонке). Здесь нет никакого подвоха, поскольку для вас в этом — никакого урона, а для меня — никакой прибыли. Просто это единственный способ для вас оперативно узнать о выходе новых версий программы, которую вы скачали.

Угол, образованный двумя лучами, исходящими из центра круга

Угол образуется, когда две линии или лучи , соединенные вместе в своих конечных точках, расходятся или расходятся. Углы варьируются от 0 до 360 градусов.

Мы часто «заимствуем» буквы из греческого алфавита, чтобы использовать их в математике. Таким образом, греческая буква «р», означающая π (пи), произносится как «пирог», представляет собой отношение длины окружности к диаметру.

Мы также часто используем греческую букву θ (тета) и произносим ее как «та-та» для обозначения углов.

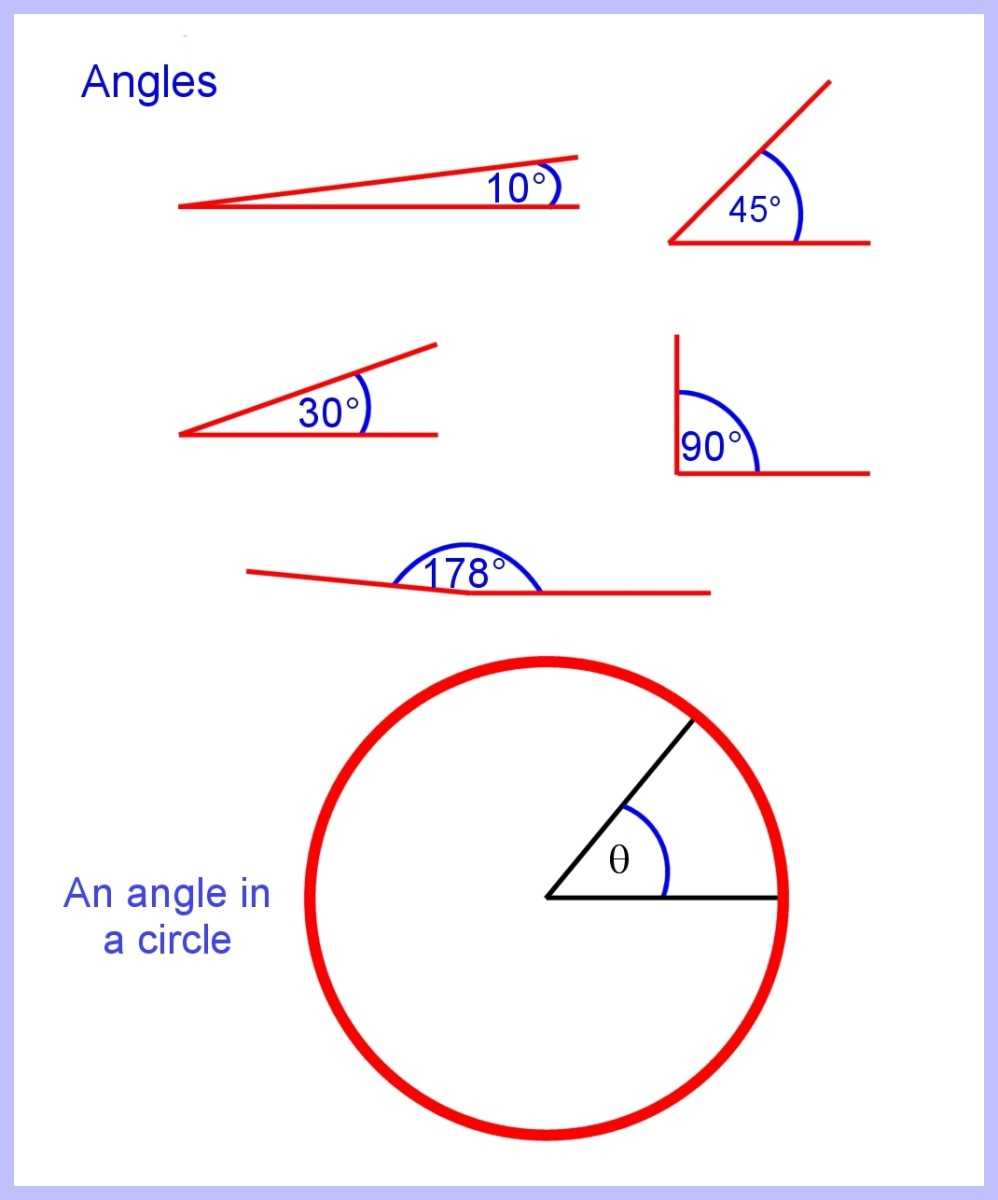
Угол, образованный двумя лучами, расходящимися из центра круга, составляет от 0 до 360 градусов.

Изображение Юджин Бреннан

360 градусов по полному кругу

Изображение Юджин Бреннан

Шаги

Метод 1

Метод 1 из 2:

Через диаметр

1. 1

   Запишите формулу для вычисления длины окружности через диаметр. Формула имеет вид: C = πd, где C — длина окружности, d — диаметр окружности. То есть длина окружности равна произведению диаметра на число π (π примерно равно 3,14).
   X
   Источник информации

   Диаметр — это отрезок, соединяющий две точки, лежащие на окружности, и проходящий через ее центр.

2. 2

   Подставьте данные вам значения в формулу и найдите длину окружности. Ниже приведен пример такого рода задачи.
   X
   Источник информации

   • Пример: у вас есть круглый бассейн диаметром 8 м, и вы хотите поставить вокруг него забор на расстоянии 6 м.
   • Чтобы рассчитать длину забора, сначала найдите диаметр окружности, то есть диаметр бассейна (8 м) плюс расстояние до забора с обеих сторон (6 м + 6 м).
   • В нашем примере диаметр равен 8 + 6 + 6 = 20 м. Подставьте это значение в формулу, нажмите на калькуляторе кнопку π (либо наберите 3,14) и вычислите длину окружности:
   • C = πd
   • C = π x 20
   • C = 62,8 м

Метод 2

Метод 2 из 2:

Через радиус

1. 1

   Запишите формулу для вычисления длины окружности через радиус. Формула имеет вид: C = 2πr, где C — длина окружности, r — радиус окружности. То есть длина окружности равна удвоенному произведению радиуса на число пи (π примерно равно 3,14).
   X
   Источник информации

   • Радиус — это любой отрезок, соединяющий точку, лежащую на окружности, с ее центром.
   • Вы наверняка заметили, что эта формула похожа на формулу C = πd. Это потому, что радиус равен половине диаметра, а диаметр, соответственно, — двум радиусам (2r).

2. 2

   Подставьте данные вам значения в формулу и найдите длину окружности. Например, вы вырезаете полоски декоративной бумаги, чтобы красиво обернуть вокруг кексов при подаче на стол. Радиус кекса равен 5 см. Подставьте это значение в формулу:
   X
   Источник информации

   • C = 2πr
   • C = 2π x 5
   • C = 10π
   • C = 31,4 см.

Советы

• Можете купить инженерный или научный калькулятор, в котором уже есть кнопка π. Так вам придется нажимать меньше кнопок, к тому же ответ будет более точным, поскольку встроенная кнопка π имеет более точное значение, чем 3,14.
• При решении задачи от вас могут потребовать писать не значок π, а его числовое значение — 3,14 (или с большим количеством знаков после запятой). Уточняйте требования у учителя.
• Чтобы вычислить окружность, зная диаметр, просто умножьте диаметр на число π.

• Радиус всегда равен половине диаметра.
  X
  Источник информации

• Не торопитесь. Помните старую пословицу: семь раз отмерь, один раз отрежь.
• Если вы не можете решить задачу, попросите помощи у друга,кого-нибудь из семьи или учителя. Они всегда помогут!
• Не забывайте перепроверять вычисления, так как любая ошибка приведет к неправильному результату.

Площади усеченных частей круга

А также полезно знать следующие геометрические элементы, связанные с кругами и окружностями:

Хорда — отрезок, соединяющий любые две точки окружности.

Сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Сектор является частью круга, а его площадь относится к площади круга так же, как и длина окружности сектора к длине всей окружности. Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.

Но площадь сектора можно вычислить и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:

где S — площадь сектора, r — радиус круга.

Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой.

Площадь сегмента можно найти по формулам:

где S — площадь сегмента, sinα — синус угла двух между радиусов до концов хорды, r — радиус круга.

Часто задаваемые вопросы о площади круга?

И конечно, стоит ответить на некоторые вопросы, которые возникают во время расчетов.

Какие есть ещё калькуляторы для круга у вас на сайте?

У нас есть разнообразные калькуляторы, в частности калькуляторы: длины окружности, диаметра и площади круга. Для последней калькулятор находится на данной странице.

Почему Пи равняется 3,1415926…, а не является «ровным» числом?

Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.

Кто впервые научился вычислять площадь круга?

Гиппократ Хиосский (не тот, в честь которого назвали клятву) первым сформулировал, что площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение. А Архимед в III веке до н. э. нашёл число Пи и продемонстрировал, что оно чуть меньше, чем 3 и 1/7.

Похожие калькуляторы

Возможно вам пригодятся ещё несколько калькуляторов по данной теме:

• Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
• Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
• Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
• Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
• Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
• Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
• Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
• Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
• Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
• Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.

Онлайн-калькулятор площади сегмента круга

Н°ÃÂþôøÃÂÃÂàÃÂÃÂð ÃÂøóÃÂÃÂð üõöôàÃÂþÃÂôþù ø ôÃÂóþù úÃÂÃÂóð.

ÃÂÃÂø þÃÂÃÂõÃÂõýøø ÃÂðÃÂÃÂø úÃÂÃÂóð ÃÂþÃÂôþù üþöýþ ÃÂðÃÂÃÂüþÃÂÃÂõÃÂàôòõ ÃÂøóÃÂÃÂÃÂ: ÃÂÃÂþ ýðàÃÂõóüõýàø ÃÂðòýþñõôÃÂõýýÃÂù ÃÂÃÂõÃÂóþûÃÂýøú, ñþúþòÃÂõ ÃÂÃÂþÃÂþýàúþÃÂþÃÂþóþ â ÃÂðôøÃÂÃÂàúÃÂÃÂóð.

ÃÂûþÃÂðôàÃÂõóüõýÃÂð üþöýþ ýðùÃÂø úðú ÃÂð÷ýþÃÂÃÂàÿûþÃÂðôõù ÃÂõúÃÂþÃÂð úÃÂÃÂóð ø ÃÂÃÂþóþ ÃÂðòýþñõôÃÂõýýþóþ ÃÂÃÂõÃÂóþûÃÂýøúð.

ÃÂûþÃÂðôàÃÂõóüõýÃÂð üþöýþ ýðùÃÂø ýõÃÂúþûÃÂúøüø ÃÂÿþÃÂþñðüø. ÃÂÃÂÃÂðýþòøüÃÂàýð ýøàñþûõõ ÿþôÃÂþñýþ.