Как найти сегмент круга

Как заработать на BestChange? Обзор партнерской программы мониторинга

Пройдя регистрацию в мониторинге обменников BestChange можно сразу начать принимать участие в партнерской программе и получать дополнительный доход от других пользователей и привлеченных партнеров:

• Доход от пользователя, который перешел по реферальной ссылке и воспользовался услугами мониторинга составляет до 0,65 USD (подробнее на скриншоте выше).
• Доход от партнеров 1-го уровня составляет 30%.
• Доход от партнеров 2-го уровня составляет 10%.

На заметку: минимальная сумма выплаты партнерского вознаграждения = 1 USD, при этом заказать выплату можно в кабинете партнера на одну из таких платежных систем: Payeer (USD, EUR, RUB), Anvanced Cash (USD, EUR, RUB), Perfect Money (USD, EUR), Яндекс Деньги, QIWI (USD, EUR, RUB), Bitcoin, PayPal (USD).

Формула длины дуги через хорду

На практике часто требуется найти длину дуги, данной на чертеже или в натуре, причем неизвестно, какую часть окружности составляет дуга и каков ее радиус. В таких случаях используют формулу Гюйгенса.

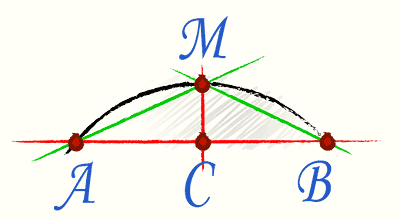
На дуге отмечают середину M. Она лежит на перпендикуляре СM, проведенном к хорде AB через середину хорды C. Далее измеряют хорды AB и AM. Длина дуги выражается через формулу Гюйгенса так:

Относительная погрешность этой формулы составляет 0.5%, когда дуга AB содержит 60°. С уменьшением угловой меры дуги процент погрешности резко падает. Для дуги в 45° относительная погрешность составляет примерно 0.02%.

Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента — по углу, по хорде, по радиусу, по высоте и длине дуги.

Вопрос-ответ:

Как использовать онлайн калькулятор площади сегмента круга?

Чтобы использовать онлайн калькулятор площади сегмента круга, введите радиус круга, а затем угол сегмента в градусах. Нажмите кнопку «Рассчитать» и вы получите площадь сегмента.

Зачем мне нужен калькулятор площади сегмента круга?

Калькулятор площади сегмента круга может быть полезен при решении задач, связанных с геометрией. Например, он может помочь вам вычислить площадь сегмента, который ограничен двумя радиусами и углом. Это может быть полезно при расчетах площадей фигур или при планировании строительства.

Можно ли использовать калькулятор площади сегмента круга на мобильном устройстве?

Да, калькулятор площади сегмента круга может быть использован на любом устройстве с доступом в интернет. Онимоспособом эиипользования onmтviajb bdgbdjgldcnsfdsqlz.

Как получить результат с точностью до десятичных знаков?

Калькулятор площади сегмента круга автоматически округляет результат до двух десятичных знаков. Если вам нужна большая точность, можно самостоятельно округлить результат до нужного количества знаков после запятой.

Что такое площадь сегмента круга?

Для вычисления площади сегмента круга необходимо знать его радиус и центральный угол, определяющий величину дуги. В зависимости от задачи, угол может быть задан в градусах, радианах или с помощью доли от общего центрального угла круга.

Формула для вычисления площади сегмента круга зависит от единиц измерения угла:

При задании угла в градусах:

S = (r^2 / 2) * (θ — sinθ)

При задании угла в радианах:

S = (r^2 / 2) * (θ — sinθ)

При задании угла в доли от общего центрального угла:

S = (θ — sinθ) * (r^2 / 2π)

Различные калькуляторы позволяют легко вычислить площадь сегоента круга, вводя необходимые данные и получая результат за считанные секунды.

Деление круга на равные части

Статья содержит два калькулятора, рассчитывающие параметры деления круга на равные по площади части радиусами и параллельными хордами

Ниже представлены два калькулятора, рассчитывающие параметры разделения круга на равные части. Сначала — традиционный калькулятор, который делит круг на равные части радиусами (примерно так, как режут пиццу или торт), под ним — нетрадиционный калькулятор, который делит круг на равные по площади части параллельными хордами. Оба калькулятора визуализируют результат рисунком. Методы расчета с формулами для обоих калькуляторов приведены ниже, под калькуляторами.

Деление круга на равные по площади части параллельными хордами

Деление круга на равные части радиусами

Традиционный и очень простой метод деления круга — по факту, нарезка равных секторов. Метод и формулы очень просты:

1. Определяем угловой размер каждого сектора в радианах, путем деления 360 градусов на нужное число секторов.

1. Определяем размер дуги сектора, перемножая радиус на угол в радианах

1. Определяем размер хорды по теореме косинусов (хорда является основанием равнобедренного треугольника с боковыми сторонами R и противолежащим углом альфа.

Собственно и всё — мы получили все характеристики для N равных секторов

Деление круга на равные части параллельными хордами

Этот способ более любопытен, чем предыдущий. Для простоты будем рассматривать верхнюю половину круга, так как с нижней все будет симметрично.

Задача состоит в определении x-вой координаты точек, через которые нужно проводить хорды (на рисунке это точки x1 и x2). Выведем для начала формулу площади куска, отсекаемого хордой слева.

Верхнюю полуокружность можно представить графиком функции y=f(x), где x — это координата вдоль оси абсцисс, а y — это функция, численно равная y координате соответствующей точки верхней полуокружности.

По теореме Пифагора получаем следующую функцию

Чтобы получить площадь фигуры, отсекаемой хордой слева, надо проинтегрировать эту функцию от -R до x. Первообразная функции равна:

Осталось определиться с константой. Нам надо, чтобы в точке с координатами -R площадь была равна нулю. Подставив -R вместо x в формулу выше, получаем

Итак, полное выражение

Теперь рассмотрим нахождение координат крайней левой точки. Нам известна площадь, которую она должна отсечь (напоминаю, речь идет о полуокружности)

Таким образом мы можем приравнять

Что дает нам такое финальное уравнение

Данное уравнение является трансцендентным, а поэтому находить координату первой точки придется численным методом, например, методом бисекции или методом Ньютона. Калькулятор использует метод Ньютона.

Вторая и последующие точки находится аналогично, путем изменения размера отсекаемой площади. Для второй точки это будет , для третьей и так далее.

Зная координаты точек, несложно рассчитать все остальные параметры, в частности, длину хорды.

Круг: сектор, сегмент. Площадь круга, сектора и сегмента

Круг — это часть плоскости, ограниченная окружностью. Центр данной окружности называется центром круга, а расстояние от центра до любой точки окружности — радиусом круга:

O  — центр круга,  OA  — радиус круга.

Площадь круга

Площадь круга равна произведению числа  π  на квадрат радиуса. Формула нахождения площади круга:

S = πr2,

где  S  — площадь круга, а  r  — радиус круга.

Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:

D = 2r,   значит   r =	D	.
2

Следовательно, формула нахождения площади круга через диаметр будет выглядеть так:

S  =  π(
D
)2  =  π

D2
 =  π

D2
 .

2
22
4

Сектор круга. Площадь сектора

Сектор — это часть круга, ограниченная двумя радиусами и дугой. Два радиуса разделяют круг на два сектора:

Чтобы найти площадь сектора, дуга которого содержит  n°,  надо площадь круга разделить на  360  и полученный результат умножить на  n.

Формула площади сектора:

S =	πr2	· n =	πr2n	,
360	360

где  S  — площадь сектора. Выражение

можно представить в виде произведения

πr2n	= n ·	πr	·	r	,
360	180	2

где	nπr	— это длина дуги сектора.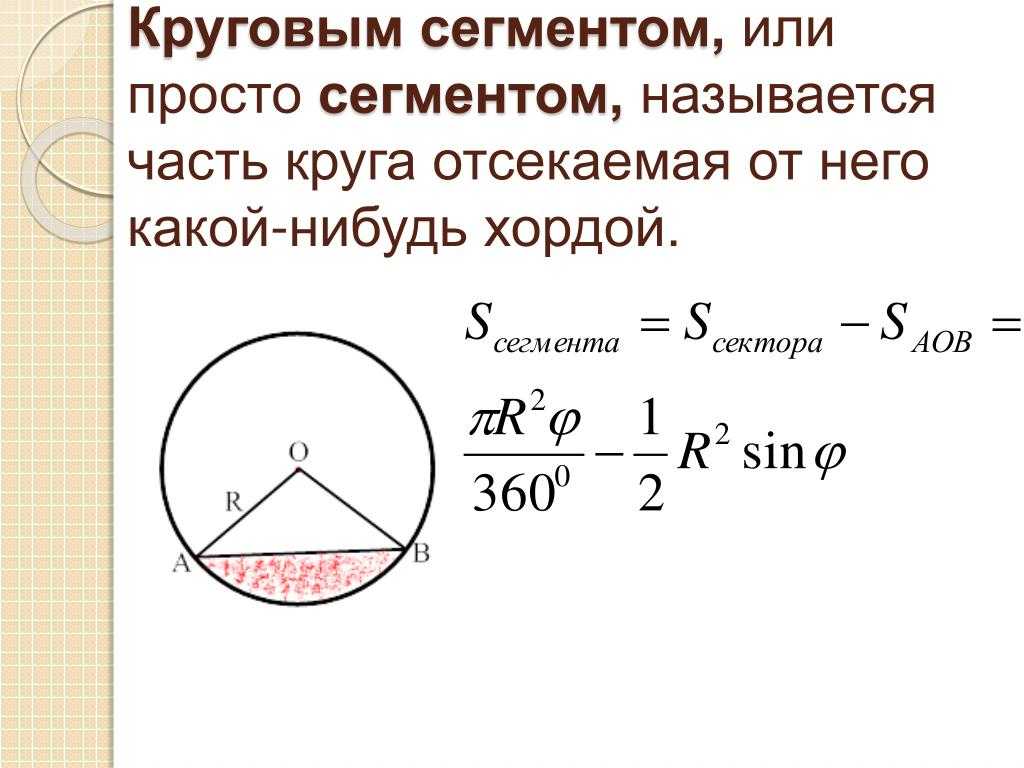
180

Следовательно, площадь сектора равна длине дуги сектора, умноженной на половину радиуса:

где  S  — это площадь сектора,  s  — длина дуги данного сектора,  r  — радиус круга.

Сегмент. Площадь сегмента

Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой. Любая хорда делит круг на два сегмента:

Площадь сегмента равна половине радиуса, умноженной на разность между дугой сегмента и половиной хорды двойной дуги.

Площадь сегмента  AMB  будет вычисляться по формуле:

где  S  — это площадь сегмента,  r  — радиус круга,  s  — длина дуги  AB,  а  BC  — длина половины хорды двойной дуги.

Деление окружности при помощи коэффициента

Для деления окружности на любое число равных частей часто пользуются приведённой в статье таблицей коэффициентов для длин хорд заданной окружности.

Деление окружности на произвольное число равных частей можно производить с помощью таблицы хорд

Для деления окружности на любое число равных частей пользуются коэффициентами, приведёнными в таблице. Длину L хорды, которую откладывают на заданной окружности.

Для получения длины хорды, нужно умножить диаметр окружности на коэффициент из таблицы.

Таблица позволяет делить окружность до 30 частей. Если требуется большее количество, то коэффициент несложно посчитать самостоятельно. Для этого делим 360 на нужное количество частей и берём синус этого числа (на большинстве калькуляторов есть такая функция). Полученный результат делим на два — это и есть наш коэффициент.

Как пользоваться онлайн калькулятором площади сегмента круга?

Онлайн калькулятор площади сегмента круга позволяет легко и быстро вычислить площадь сегмента круга по заданным параметрам.

Для использования калькулятора выберите единицу измерения длины (например, сантиметры или метры) и введите значение радиуса круга и угла сегмента. Угол должен быть задан в градусах.

После ввода всех необходимых данных нажмите кнопку «Рассчитать». Калькулятор мгновенно выведет результат — площадь сегмента круга.

Помните, что результат будет выведен в квадратных единицах измерения длины, так как площадь имеет размерность величины в квадрате. Например, если вы выбрали сантиметры в качестве единицы измерения, площадь будет выведена в квадратных сантиметрах.

Также обратите внимание, что угол сегмента круга должен быть меньше или равен 180 градусам. Если угол превышает 180 градусов, площадь сегмента будет равна площади всего круга

Пример использования:

Предположим, у нас есть круг радиусом 10 см, и мы хотим найти площадь сегмента с углом в 90 градусов. Вводим значения — радиус: 10, угол: 90, единица измерения: сантиметры. После нажатия кнопки «Рассчитать» калькулятор выведет результат — площадь сегмента равна 78,54 квадратных сантиметра.

Формула площади сегмента круга через радиус и длину дуги круга, высоту и основание треугольника

S=12⋅R⋅s−12⋅h⋅aS=frac{1}{2}cdot Rcdot s-frac{1}{2}cdot hcdot aS=21​⋅R⋅s−21​⋅h⋅a

RRR — радиус круга;sss — длина дуги;hhh — высота равнобедренного треугольника;aaa — длина основания этого треугольника.

Пример

Дан круг, его радиус, численно равный 5 (см.), высота, которая проведена к основанию треугольника, равная 2 (см.), длина дуги 10 (см.). Найти площадь сегмента круга.

Решение

R=5R=5R=5h=2h=2h=2s=10s=10s=1

Для вычисления площади нам не хватает только основания треугольника. Найдем его по формуле:

a=2⋅h⋅(2⋅R−h)=2⋅2⋅(2⋅5−2)=8a=2cdotsqrt{hcdot(2cdot R-h)}=2cdotsqrt{2cdot(2cdot 5-2)}=8a=2⋅h⋅(2⋅R−h)​=2⋅2⋅(2⋅5−2)​=8

Теперь можно вычислить площадь сегмента:

S=12⋅R⋅s−12⋅h⋅a=12⋅5⋅10−12⋅2⋅8=17S=frac{1}{2}cdot Rcdot s-frac{1}{2}cdot hcdot a=frac{1}{2}cdot 5cdot 10-frac{1}{2}cdot 2cdot 8=17S=21​⋅R⋅s−21​⋅h⋅a=21​⋅5⋅1−21​⋅2⋅8=17 (см. кв.)

Ответ: 17 см. кв.

Теория

Площадь сегмента окружности через угол и радиус

Чему равна площадь сегмента окружности S_ск, если её радиус r, а угол сегмента α ?

В градусах:

S_ск = r²2 ⋅ (π ⋅ α180° — sin α)

В радианах:

S_ск = r²2 ⋅ (α — sin α)

Пример

К примеру, посчитаем площадь сегмента круга, имеющего радиус r = 2 см, а угол сегмента ∠α = 45°:

S_ск = 2²2 ⋅ (3.14 ⋅ 45180 — sin 45) = 2 ⋅ (0.785 — 0.707) = 0.156 см²

Площадь сегмента окружности через хорду и высоту сегмента

Чему равна площадь сегмента окружности S_ск, если длина хорды c, а высота сегмента h ?

Чтобы посчитать площадь сегмента, нам для начала потребуется вычислить радиус окружности r и угол сегмента α. А затем воспользоваться формулой площади сегмента из предыдущего параграфа.

Радиус круга:

r = c² + 4h²8h

Угол сегмента:

∠α = 2 ⋅ arcsinc2r

Пример

К примеру, посчитаем площадь сегмента круга, имеющего высоту h = 2 см и длину хорды c = 5 см:

r = 5² + 4⋅2²8⋅2 = 25 + 1616 = 2.5625 см∠α = 2 ⋅ arcsin52 ⋅ 2.5625 = 2 ⋅ arcsin 0.9756 ≈ 2.7 radS_ск = 2.5625²2 ⋅ (2.7 — sin 2.7) = 3.2832 ⋅ (2.7 — 0,427) = 7.46 см²

Площадь сегмента окружности через высоту и радиус (или диаметр)

Чему равна площадь сегмента окружности S_ск, если его высота h, а радиус r ?

Если нам известен не радиус, а диаметр, то делим его на 2 и получаем радиус (r = d ÷ 2).

Далее нам остаётся определить угол сегмента α. А затем воспользоваться формулой площади сегмента, описанной выше.

Угол сегмента:

∠α = 2 ⋅ arccosr — hr

Пример

К примеру, посчитаем площадь сегмента круга, имеющего высоту h = 1 см, а диаметр окружности d = 4 см:

r = 4 ÷ 2 = 2 см

∠α = 2 ⋅ arccos2 — 12 = 2 ⋅ arccos 0.5 = 2.094 radS_ск = 2²2 ⋅ (2.094 — sin 2.094) = 2 ⋅ (2.094 — 0.866) = 2.456 см²

📌 Формула площади круга — через радиус, диаметр, длину окружности

Формула площади круга — одно из основных математических понятий, необходимых для решения задач, связанных с геометрией и физикой. При этом существует несколько способов вычисления площади круга, каждый из которых основывается на различных характеристиках самого круга.

Через радиус

Основная формула для вычисления площади круга основывается на радиусе данного круга. Радиус — это расстояние от центра круга до любой его точки. Формула площади круга при использовании радиуса записывается следующим образом:

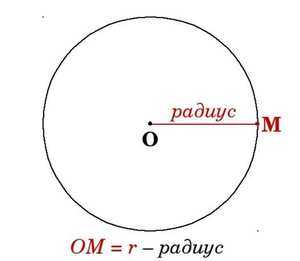
где S — это площадь круга, π (пи) — математическая константа, приближенно равная 3,14159, r — радиус круга.

Пример вычисления площади круга через радиус:Пусть радиус круга равен 5. Применяя формулу S = π * r^2, получаем S = 3.14159 * 5^2 = 3.14159 * 25 = 78.53975.Таким образом, площадь круга с радиусом 5 равна 78.53975 квадратных единиц.

Через диаметр

Также существует формула площади круга, представленная через диаметр. Диаметр — это отрезок, соединяющий две точки на окружности и проходящий через ее центр.

Формула площади, использующая диаметр, записывается следующим образом:

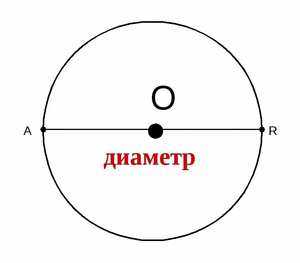
где d — диаметр кругаπ (пи) — математическая константа, приближенно равная 3,14159

Пример вычисления площади круга через диаметр:Пусть диаметр круга равен 10. Используя формулу S = (π * d^2) / 4, получаем S = (3.14159 * 10^2) / 4 = (3.14159 * 100) / 4 = 31.4159. Таким образом, площадь круга с диаметром 10 равна 31.4159 квадратных единиц.

Через длину окружности

Еще один способ вычисления площади круга основан на длине его окружности.Окружность — это геометрическое место всех точек плоскости, которые находятся на одинаковом расстоянии от данной точки, называемой центром окружности.

Формула площади круга на основе длины окружности записывается следующим образом:

где S — площадь круга, C — длина окружности.

Исследования в области площади круга показывают, что формула площади на основе радиуса является самой популярной и широко используется в различных научных и практических задачах.Однако, формулы на основе диаметра и длины окружности также применяются при решении определенных задач или при отсутствии информации о радиусе.

Важно отметить, что площадь круга всегда будет положительным числом, так как она представляет собой меру площади внутри круга. Невозможно иметь круг с отрицательной площадью или площадью, равной нулю

Итак, формула площади круга — это основной инструмент для вычисления площади данной геометрической фигуры. Она может быть выражена через радиус, диаметр или длину окружности. При этом, каждый из этих способов имеет свои особенности и применяется в различных ситуациях. Корректное использование формулы позволяет получить точные результаты при решении математических и физических задач, связанных с кругами.

Сектор круга и сегмент

Есть два основных «кусочка» круга:

Кусочек «пиццы» называется Сектор .
И сегмент , который отсечен от круга «хордой» (линия между двумя точками на окружности).

Квадрант и Полукруг — это два особых типа сектора:

Полукруг — это полукруг .

Четверть круга — это , а Квадрант .

Площадь сектора

Вы можете рассчитать площадь сектора, сравнив его угол с углом полного круга.

Примечание: мы используем радианы для углов.

Это рассуждение:

Круг имеет угол 2π и площадь: πr 2

Сектор имеет угол θ вместо 2π, поэтому его площадь составляет: θ 2π × πr 2

Что можно упростить до: θ 2 × r 2

Площадь сектора = θ 2 × r 2 (когда θ в радианах)

Площадь сектора = θ × π 360 × r 2 (когда θ в градусах)

Площадь сегмента

Площадь сегмента — это площадь сектора за вычетом треугольника (здесь показан голубым).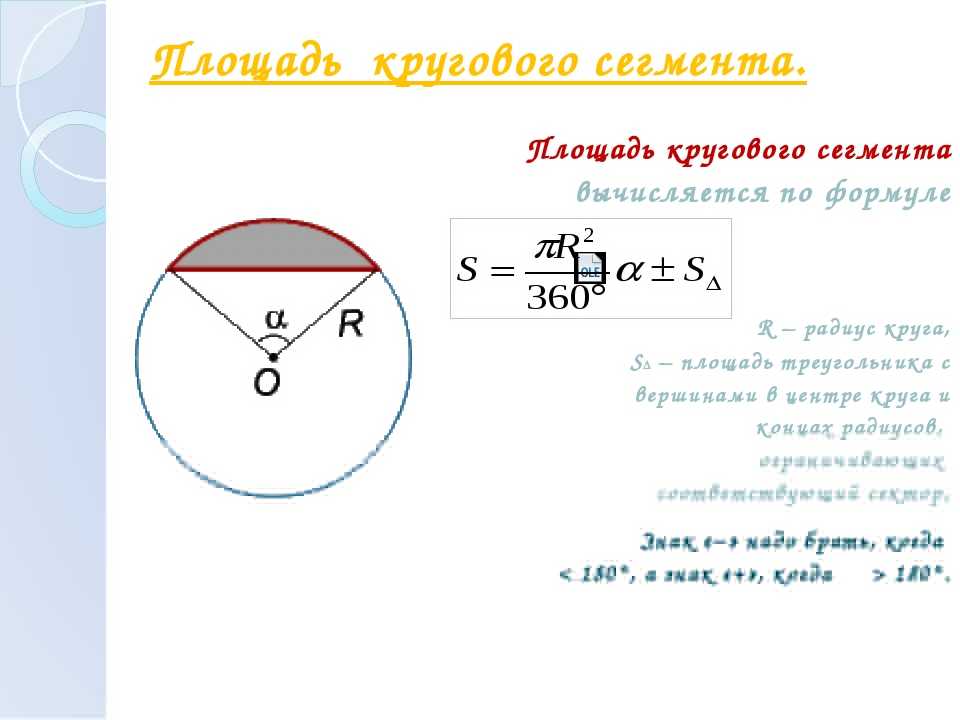

Есть длинная причина, но результатом является небольшая модификация формулы Сектора:

Площадь сегмента = θ — грех (θ) 2 × r 2 (когда θ в радианах)

Площадь сегмента = ( θ × π 360 — sin (θ) 2 ) × r 2 (когда θ в градусах)

Теоремы о круге — Математика GCSE Revision

Теоремы

В этом разделе объясняется теорема окружности, включая касательные, сектора, углы и доказательства.

В видео ниже показаны правила, которые нужно помнить при построении теорем о кругах.

Равнобедренный треугольник

Два радиуса и хорда образуют равнобедренный треугольник.

Биссечение перпендикулярной хорды

Перпендикуляр от центра окружности к хорде всегда будет делить хорду пополам (разделять его на две равные длины).

Углы, расположенные на одной дуге

Углы, образованные из двух точек на окружности, равны другим углам в той же дуге, образованным из этих двух точек.

Угол по полукругу

Углы, образованные проведением линий от концов диаметра круга к его окружности, образуют прямой угол.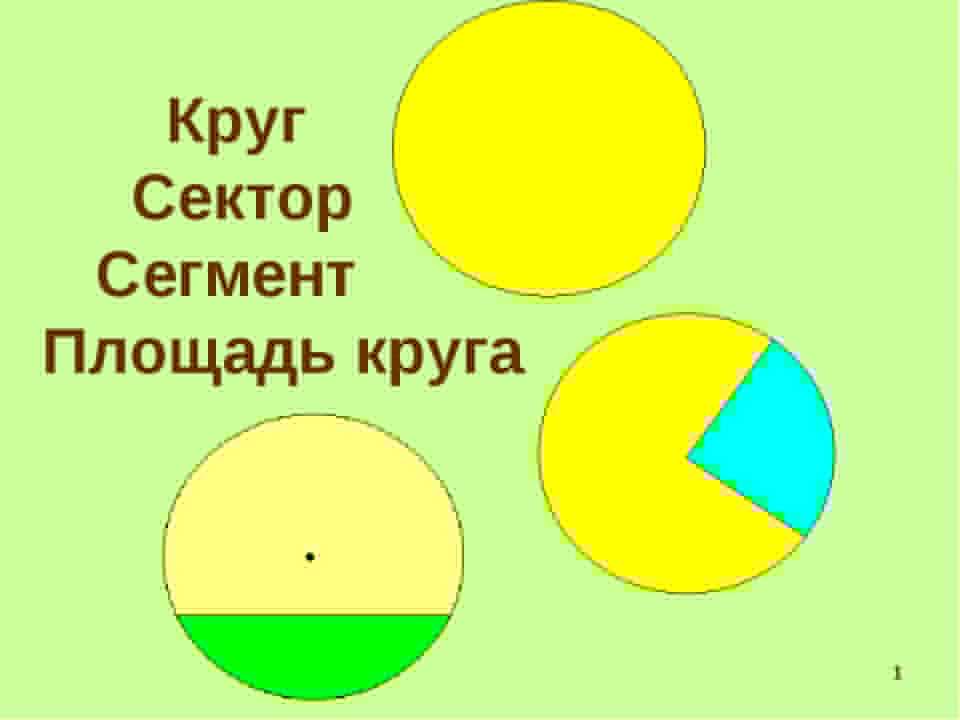

c — это прямой угол

Проба

Мы можем разделить треугольник пополам, проведя линию от центра круга до точки на окружности, которой соприкасается наш треугольник.

Мы знаем, что каждая из линий, являющихся радиусом круга (зеленые линии), имеет одинаковую длину. Следовательно, каждый из двух треугольников равнобедренный и имеет пару равных углов.

Но все эти углы вместе должны составлять 180 °, так как они являются углами исходного большого треугольника.

Следовательно, x + y + x + y = 180, другими словами 2 (x + y) = 180. и поэтому x + y = 90. Но x + y — это размер угла, который мы хотели найти.

Касательные

Касательная к окружности — это прямая линия, которая касается окружности только в одной точке (поэтому она не пересекает окружность, а только касается ее).

Касательная к окружности образует прямой угол с радиусом окружности в точке контакта касательной.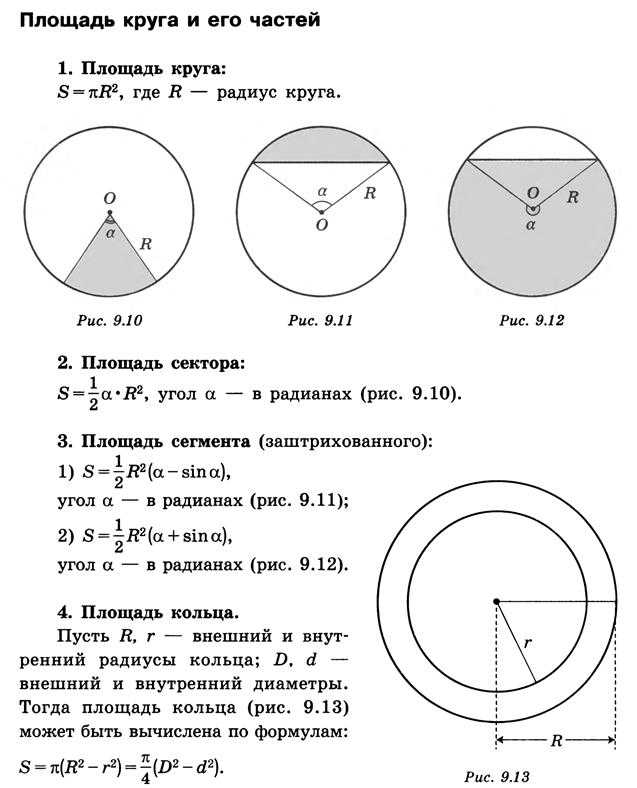

Кроме того, если две касательные нарисованы на окружности и они пересекаются, длины этих двух касательных (от точки, где они касаются круга, до точки, где они пересекаются) будут одинаковыми.

Угол в центре

Угол, образованный в центре круга линиями, начинающимися из двух точек на окружности окружности, в два раза больше угла, образованного на окружности окружности линиями, берущими начало в тех же точках. то есть a = 2b .

Проба

Возможно, вам придется доказать этот факт:

OA = OX, поскольку оба они равны радиусу круга.Следовательно, треугольник AOX равнобедренный, поэтому ∠OXA = a . Аналогично, OXB = b

Поскольку в сумме углы в треугольнике равны 180, мы знаем, что ∠XOA = 180 — 2a Точно так же ∠BOX = 180 — 2b Поскольку углы вокруг точки в сумме составляют 360, мы имеем ∠AOB = 360 — ∠XOA — ∠BOX = 360 — (180 — 2a) — (180 — 2b) = 2a + 2b = 2 (a + b) = 2 ∠AXB

Теорема об альтернативном сегменте

На этой диаграмме показана теорема об альтернативном сегменте .

Проба

Возможно, вам придется доказать теорему об альтернативном отрезке:

Мы используем факты о связанных углах

Касательная составляет угол 90 градусов с радиусом окружности, поэтому мы знаем, что ∠OAC + x = 90. Угол в полукруге равен 90, поэтому ∠BCA = 90. Углы в треугольнике складываем до 180, поэтому ∠BCA + ∠OAC + y = 180 Следовательно, 90 + ∠OAC + y = 180 и, следовательно, ∠OAC + y = 90 Но OAC + x = 90, поэтому ∠OAC + x = ∠OAC + y Следовательно, x = y

Циклический четырехугольник

Циклический четырехугольник — это четырехсторонняя фигура в окружности, каждая вершина (угол) четырехугольника которой касается окружности окружности.Противоположные углы такого четырехугольника в сумме составляют 180 градусов.

Площадь сектора и длина дуги

Если радиус окружности равен r, Площадь сектора = πr 2 × A / 360 Длина дуги = 2πr × A / 360

Другими словами, площадь сектора = площадь круга × A / 360 длина дуги = длина окружности × A / 360

Для получения дополнительной информации об определениях кругов щелкните здесь

Сегмент круга

Данный калькулятор считает параметры сегмента круга, а именно:

• длину дуги (L),
• длину хорды (C),
• площадь (S),
• высоту (h),

Перед вами 2 калькулятора, чтобы рассчитать параметры сегмента:

1) сегмент круга решается с помощью радиуса (R) и угла (A).

2) сегмент круга находим с помощью высоты и длины хорды.

Однако, как справедливо заметил наш пользователь:«на практике hourто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:

Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:

Далее зная радиус и длину хорды, легко найти угол сегмента по формуле:

Остальные параметры сегмента, вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.

Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:

Альтернативы онлайн калькулятору площади сегмента круга

Если вам требуется вычислить площадь сегмента круга, но вы не хотите использовать онлайн калькулятор, есть несколько альтернативных способов для выполнения данного расчета:

1. Использование формулы. Если у вас есть математическая формула для вычисления площади сегмента круга, вы можете рассчитать его вручную, используя эту формулу. Это может потребовать некоторых математических навыков и знаний о геометрии, но это может быть полезным способом получить результат без использования онлайн калькулятора.
2. Использование программного обеспечения. Вместо онлайн калькулятора, вы можете установить специальное программное обеспечение на свой компьютер, которое поможет вам рассчитать площадь сегмента круга. Такие программы обычно включают в себя широкий набор математических формул и геометрических алгоритмов, что позволяет вычислять сложные площади и объемы.
3. Консультация с профессионалами. В случае, если вам необходимо рассчитать площадь сегмента круга для конкретной задачи или проекта, вы можете обратиться к специалистам в данной области (например, инженерам или математикам). Они смогут предоставить вам точные результаты, основанные на своих знаниях и профессиональном опыте.

Онлайн калькулятор площади сегмента круга является удобным инструментом для быстрого вычисления данной величины. Однако, если вы хотите избежать использования таких инструментов или нуждаетесь в более точных результатов, вам доступны альтернативные способы расчета площади сегмента круга.