Как найти радиус шара, если известен его объем?

Длина и площадь

Окружность и круг — две фигуры, изучаемые в геометрии плоскости. Они имеют общую форму и определяются с помощью основных элементов — радиуса и центра. Длина окружности и площадь круга являются важными характеристиками этих фигур и вычисляются по определенным формулам.

Длина окружности можно вычислить с помощью формулы: L = 2πr, где L — длина окружности, r — радиус окружности. Радиус — это расстояние от центра окружности до любой точки на ней. Формула позволяет нам определить длину окружности, зная ее радиус. Таким образом, длина окружности выражается через число π (3,14) и умножается на радиус.

Площадь круга можно вычислить с помощью формулы: S = πr^2, где S — площадь круга, r — радиус круга. Площадь круга определяется как участок плоскости, ограниченный окружностью. Формула позволяет нам определить площадь круга, зная ее радиус. Площадь выражается через число π (3,14) и умножается на квадрат радиуса.

Теоретически окружность и круг неразрывно связаны друг с другом. Окружность — это граница круга, а круг — это фигура, заключенная внутри окружности. Однако, в геометрии плоскости, окружность и круг имеют разные характеристики и свойства, включая их длину и площадь. Понимание этих характеристик позволяет более глубоко изучать и использовать окружность и круг в различных областях науки и практики.

Расчет длины окружности

Окружность является геометрической фигурой, которая находится в плоскости и состоит из точек, равноудаленных от ее центра. Важнейшим параметром окружности является ее диаметр, который представляет собой максимальное расстояние между двумя точками на окружности, проходящими через ее центр.

Длина окружности может быть рассчитана по формуле, которая основана на теории геометрии и связана с радиусом окружности. Радиус представляет собой расстояние от центра окружности до любой точки на ее границе. Формула для расчета длины окружности выглядит следующим образом: L = 2πr, где L — длина окружности, π — математическая константа, примерное значение которой равно 3,14, а r — радиус окружности.

Размер длины окружности напрямую зависит от размера ее радиуса. Чем больше радиус, тем длиннее будет окружность, и наоборот. Точная длина окружности может быть рассчитана с высокой точностью при помощи математических функций или приближенно, используя значение π при округлении его до десятичных знаков.

Расчет площади круга

Геометрия изучает фигуры на плоскости, такие как круг. Круг — это геометрическая фигура, состоящая из всех точек на плоскости, которые находятся на одинаковом расстоянии от центра.

Основными понятиями, связанными с кругом, являются радиус и диаметр. Радиус — это расстояние от центра круга до любой точки его окружности, а диаметр — это удвоенный радиус.

Для расчета площади круга используется теория геометрии. Формула для расчета площади круга основана на длине его радиуса. Площадь круга равна произведению квадрата его радиуса на число π (пи).

Формула для расчета площади круга выглядит следующим образом: площадь = π * (радиус)^2. В данной формуле π — математическая константа, приблизительно равная 3.14159.

Для удобства расчетов площади круга можно использовать таблицу, где указывается значение радиуса и соответствующая площадь круга. Также можно воспользоваться онлайн-калькулятором для расчета площади круга, который автоматически выполнит необходимые математические операции.

Уравнение сферы

В планиметрии мы уже изучали уравнения линии. Так назывались ур-ния с двумя переменными, каждое решение которых соответствовало точке на координатной плос-ти, принадлежавшей заданной линии. Если же точка не принадлежала линии, то ее координаты решением соответствующего ур-ния не являлись. В частности, нам удалось получить уравнения прямой и окружности.

Аналогично в стереометрии вводится понятие уравнения поверхности. Так как в пространстве используются уже три координаты (х, у и z), то ур-ния поверхности содержат три переменных. Координаты всякой точки, принадлежащей поверхности, будут являться решениями ур-ния этой поверхности. И наоборот, координаты точки, не принадлежащей поверхности, будут обращать ур-ние поверхности в неверное равенство.

Выведем ур-ние сферы. Пусть ее центр располагается в точке С с координатами (х, у, z), а радиус обозначен как R. Возьмем произвольную точку А на сфере. По определению сферы расстояние между А и С должно составлять R:

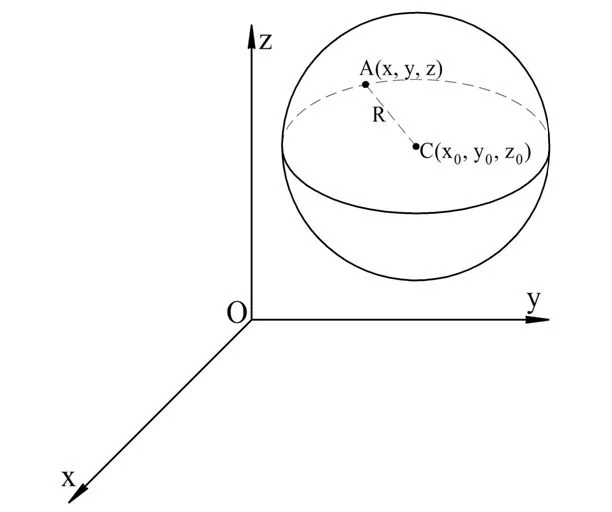
Мы уже знаем формулу для расчета расстояния между А и С:

Точки, координаты которых удовлетворяют этому неравенству, находятся от центра сферы на расстоянии меньше ее радиуса. Это значит, что они находятся внутри сферы, то есть принадлежат шару, чьей поверхностью является рассматриваемая сфера. Если же координаты точки удовлетворяют неравенству

то можно утверждать, что точка находится вне пределов сферы, то есть она не принадлежит ни сфере, ни шару.

Задание. Напишите уравнение сферы, центр которой располагается в точке (2; – 4; 7) и чей радиус равен 3.

Решение. Здесь мы просто подставляем координаты центра сферы и ее радиус в ур-ние сферы:

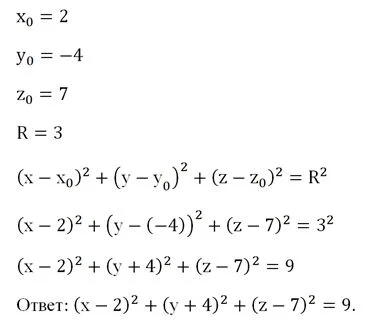
Задание. Есть сфера с радиусом 9, чей центр располагается в точке О(2; 3; 4). Определите, какие из следующих точек будут принадлежать этой сфере: А(1; 7; – 4), В(0; 6; 10), С(– 2; – 1; 11), D(5; 6; 8).

Решение. Сначала составляем уравнение сферы, описанной в условии:

Равенство неверное, значит, В не располагается на сфере (более того, раз 49 < 81, то можно утверждать, что точка располагается внутри сферы). Далее проверяем точку С(– 2; – 1; 11):

Задание. Докажите, что ур-ние

является ур-нием сферы, после чего определите радиус этой сферы.

Решение. Здесь необходимо выполнить некоторые преобразования ур-ния, чтобы оно стало похожим на ур-ние сферы. Для этого используем формулы квадратов суммы и разности:

Пример

Расчет площади поверхности Земли может быть интересным примером для применения калькулятора расчета площади шара. Земля приближенно является геоидом, то есть ее форма приближенно сферическая с некоторыми нерегулярностями.

Для расчета площади поверхности Земли можно использовать радиус, который обычно указывают в километрах. Приближенное значение радиуса Земли составляет около 6 371 километр.

Применяя формулу для расчета площади поверхности шара, получим:

S = 4πr2
S = 4 * 3.14159 * (6,371)2
S ≈ 4 * 3.14159 * 40,518,241
S ≈ 509,904,080 квадратных километров

Таким образом, приближенная площадь поверхности Земли составляет около 509,904,080 квадратных километров.

Отметим, что это приближенное значение, так как форма Земли не является точной сферой. В реальности форма Земли более сложная и неоднородная, и точное измерение ее поверхности требует более сложных геодезических методов.

Вопросы и ответы

Вот некоторые вопросы, которые могут возникнуть при использовании калькулятора площади шара (сферы) и ответы на них.

Какова формула для расчета площади поверхности шара?

Формула для расчета площади поверхности шара выглядит так: S = 4πr^2, где S — площадь поверхности, π — математическая константа (приблизительное значение 3.14159), r — радиус шара.

Как использовать калькулятор площади шара?

Введите значение радиуса шара в соответствующее поле на калькуляторе и нажмите кнопку «Рассчитать». Калькулятор автоматически применит формулу и выдаст результат — площадь поверхности шара.

Могу ли я использовать дробные значения радиуса?

Да, вы можете использовать дробные значения радиуса при расчете площади поверхности шара. Просто введите соответствующее десятичное число в поле радиуса.

В каких единицах измерения будет выведен результат площади?

Результат площади будет выведен в квадратных единицах измерения, соответствующих используемой системе измерения радиуса (например, квадратных метрах, квадратных сантиметрах и т.д.).

Можно ли использовать калькулятор для других форм, а не только для шара?

Нет, калькулятор расчета площади шара предназначен исключительно для расчета площади поверхности шара. Для расчета площади других форм (например, цилиндра, конуса и т.д.) вы можете использовать другие наши калькуляторы.

Можно ли использовать калькулятор для расчета объема шара?

Нет, калькулятор площади шара предназначен только для расчета площади его поверхности. Для расчета объема шара используется другая формула: V = (4/3)πr^3.

Как найти центр и радиус сферы

Круги и сферы универсальны по своей природе и представляют собой двумерные и трехмерные версии одной и той же существенной формы. Круг — это замкнутая кривая на плоскости, тогда как сфера — это трехмерная конструкция. Каждый из них состоит из набора точек, которые все находятся на одинаковом фиксированном расстоянии от центральной точки. Это расстояние называется радиусом.

Круги и сферы симметричны, и их свойства имеют неограниченные жизненные приложения в физике, технике, искусстве, математике и любых других человеческих начинаниях. Если вы сталкиваетесь с математической проблемой, связанной со сферой, вам нужна некоторая довольно рутинная математика, чтобы найти центр и радиус сферы, если у вас есть некоторая другая информация о сфере.

Уравнение сферы с центром и радиусом R

Общее уравнение для площади круга: A = π_r_ 2 , где r (или R ) — радиус. Наибольшее расстояние по кругу или сфере называется диаметром ( D ) и вдвое больше радиуса. Расстояние вокруг круга, известное как окружность, задается как 2π_r_ (или, что то же самое, π_D_); та же формула справедлива для самого длинного пути вокруг сферы.

В стандартной системе координат x -, y -, z — центр любой сферы может быть удобно расположен в начале координат (0, 0, 0). Это означает, что если радиус равен R , все точки ( R , 0, 0), (0, R , 0) и (0, 0, R ) лежат на поверхности сферы, как и (- R , 0, 0), (0, -R , 0) и (0, 0, -R ).

Другая информация о сферах

Сферы, как и плоскости, имеют площадь поверхности, которая изогнута. Земля и другие планеты являются примерами сфер, у которых есть поверхности, которые часто функционально рассматриваются как двумерные, потому что любая одна часть земной поверхности разумного размера выглядит как таковая в масштабе операций размером с человека.

Площадь поверхности сферы определяется как A = 4π_r_ 2, а ее объем определяется как V = (4/3) π_r_ 3 . Это означает, что если у вас есть значение для области или объема, чтобы найти центр и радиус сферы, вы можете сначала вычислить r , а затем точно знать, как далеко вы должны пройти по прямой линии до достижения центра сферы, при условии, что вы не можете установить (0, 0, 0) в качестве центра для удобства.

Земля как сфера

Земля в буквальном смысле не является сферой, так как она сплющена сверху и снизу отчасти благодаря тому, что она вращалась в течение миллиардов лет. Линия, образующая окружность вокруг самой жирной части в середине, имеет специальное название — экватор.

Проблема: Учитывая, что радиус Земли всего лишь 4000 миль, оцените окружность, площадь поверхности и объем.

C = 2 × 4 000 = около 25 000 миль

A = 4π × 4000 2 = около 2 × 10 8 миль 2 (200 миллионов квадратных миль)

A = (4/3) × π × 4000 3 = около 2, 56 × 10 10 миль 3 (256 миллиардов кубических миль)

подсказки

Для справки: хотя крупные страны, Соединенные Штаты, Китай и Канада, кажется, занимают значительную долю поверхности Земли на земном шаре, каждая из этих стран имеет площадь от 3 до 4 миллионов квадратных миль, или меньше 2 процента поверхности Земли в каждом случае.

Оценка объема сферы

Как показывает приведенный выше пример, если вы хотите найти объем сферы, а у вас нет удобного уравнения для устройства калькулятора сфер, вы можете оценить это, помня, что π приблизительно равно 3 (фактически 3, 141…) и что (4/3) Поэтому π близко к 4. Если вы можете получить хорошую оценку куба радиуса, вы будете достаточно близки для «приблизительных» целей в отношении объема.

Как найти и рассчитать вес сферы

Вес сферы может быть найден с помощью средств, отличных от весов. Сфера — это трехмерный объект со свойствами, полученными из окружности, такими как формула объема, 4/3 * pi * radius ^ 3, которая имеет математическую константу pi, отношение длины окружности к ее диаметру. что примерно .

Как найти радиус сферы при заданном объеме

Радиус сферы скрывается внутри ее абсолютной округлости. Радиус сферы — это длина от центра сферы до любой точки на ее поверхности. Радиус является идентифицирующей чертой, и из него могут быть вычислены другие измерения сферы, включая ее окружность, площадь поверхности и объем. Формула .

Как найти объем сферы в единицах пи

Сфера — это трехмерный круглый объект, такой как мраморный или футбольный мяч. Объем представляет пространство, окруженное объектом. Формула для объема сферы в 4/3 раза больше пи, умноженного на радиус куба. Кубизировать число означает умножить его на себя в три раза, в этом случае радиус умножить на радиус .

Пересечение двух сфер

Пусть есть две пересекающиеся сферы с центрами в точках О₁ и О₂ с радиусами R₁и R₂соответственно. Какую форму будет иметь линия L, по которой они пересекаются?

Эта линия является множеством точек, которые принадлежат как первой, так и второй сфере. Обозначим две произвольные точки этой линии буквами А и В:

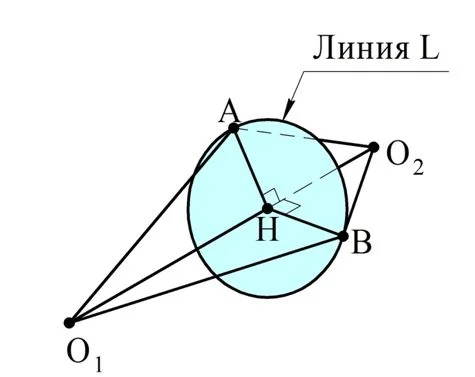
Проведем радиусы О₁А, О₁В, О₂А и О₂В. Теперь сравним ∆АО₁О₂ и ∆ВО₁О₂. Сторона О₁О₂ у них общая, а другие стороны попарно равны как радиусы сфер:

Получается, что ∆АО₁О₂ и ∆ВО₁О₂ равны. Теперь из точек А и В опустим высоты на прямую О₁О₂. Из равенства ∆АО₁О₂ и ∆ВО₁О₂ вытекает два факта:

эти высоты упадут в одну точку Н;
эти высоты будут одинаковы, то есть АН = НВ.

Другими словами, А и В равноудалены от Н. Получается, что точки А и В находятся на окруж-ти, центр которой – точка Н. Заметим, что О₁О₂ – перпендикуляр к плоскости окружности, ведь О₁О₂⊥АН и О₁О₂⊥ВН.

Точки А и В были выбраны произвольно, поэтому можно утверждать, что любые точки линии L будут находиться на одной окруж-ти. Докажем и обратное утверждение – любая точка, лежащая на этой окруж-ти, будет принадлежать линии L. Возьмем на окруж-ти какую-нибудь точку С и построим радиус НС:

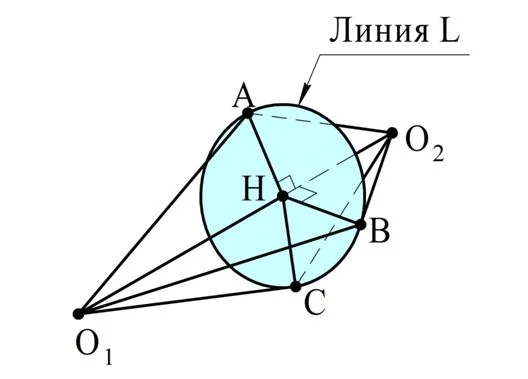
Теперь сравним ∆О₁НС и ∆О₁НА. Они прямоугольные, ведь О₁Н – перпендикуляр к плос-ти окружности. Катет О₁Н у них общий, а катеты АН и НС одинаковы как радиусы окруж-ти. Значит, ∆О₁НС и ∆О₁НА равны, и потому

Это равенство означает, что С принадлежит сфере с центром в О₁. Аналогично рассмотрев ∆О₂НС и ∆О₂НА, можно показать, что С также принадлежит и второй сфере. Тогда С принадлежит пересечению этих сфер.

Итак, всякая точка линии L лежит на окруж-ти с центром Н, и наоборот, каждая точка этой окруж-ти лежит на линии L. Это означает, что L как раз и является этой окружностью.

Отметим ещё один факт: по неравенству треугольника отрезок О₁О₂должен быть меньше суммы отрезков О₁А и О₂А, то есть суммы радиусов сфер.

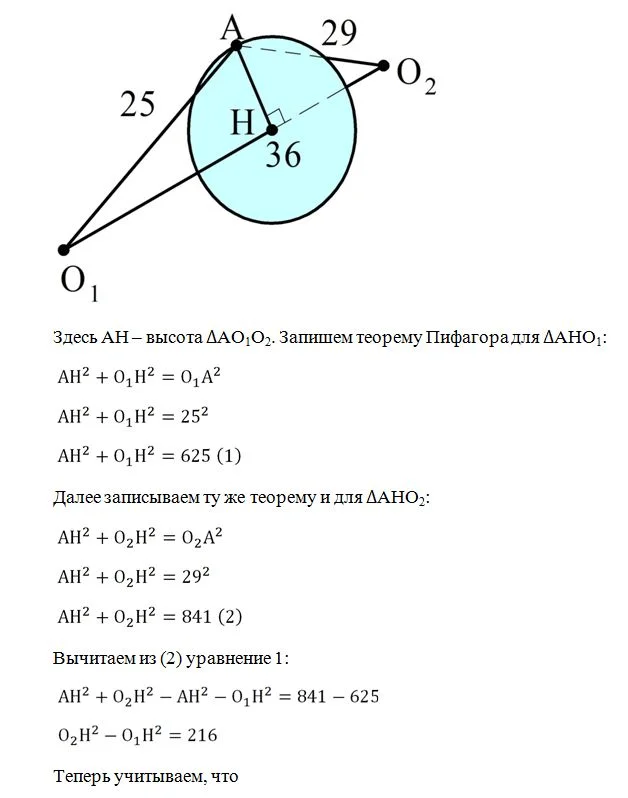
Задание. Сферы имеют радиусы 25 см и 29 см, а расстояние между их центрами составляет 36 см. Вычислите радиус окруж-ти, по которой они пересекаются.

Решение. Пусть А – одна их точек сечения. Искомый радиус обозначим как АН. В итоге получим такую картинку:

Куб — свойства, виды и формулы » Kupuk.

Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.

Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:

многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;
прямая призма, все грани которой есть квадраты;
прямоугольный параллелепипед, все рёбра которого равны.

Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.

Элементы куба

Основными элементами многогранника считаются грани, рёбра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.

Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.

Грани куба попарно перпендикулярны, являются квадратами, равны между собой.

Ребро

Линии пересечения сторон называются рёбрами.

Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.

Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.

Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата.

Центр куба

Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.

Это есть центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.

Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.

Диагональ куба — одна из осей симметрии.

Все диагонали куба равны между собой и точкой пересечения делятся пополам.

Диагональ грани куба

Длина диагонали грани в √2 раз больше ребра, то есть:

Эта формула доказывается также с помощью теоремы Пифагора.

Такая сфера имеет центр, совпадающий с центром куба.

Радиус равен половине ребра:

Координаты вершин куба

В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.

Наиболее часто используют следующий способ.

Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).

Свойства куба

Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.

Построение сечений необходимо для решения многих задач.

Прочие свойства:

у куба все грани равны, являются квадратами;
у куба все рёбра равны;
один центр и несколько осей симметрии.

Свойства

Если описать вокруг куба сферу, то ее диаметр будет соединять противоположные вершины куба, образуя диагональ куба. Таким образом, радиус описанной сферы куба равен половине диагонали, следовательно, сама диагональ куба равна удвоенному радиусу описанной сферы. (рис.2.3) D=2R

Так как эта же диагональ связывает теоремой Пифагора в прямоугольном треугольнике диагональ стороны куба и ребро куба, то становится возможным вычислить и их через радиус описанной сферы куба, используя формулы диагонали. D=a√3 a=D/√3=2R/√3 a^2+d^2=D^2 (2R/√3)^2+d^2=(2R)^2 d^2=(8R^2)/3 d=√(8/3) R

Чтобы вычислить площадь грани куба, нужно рассмотреть ее в плоскости. Стороной куба является квадрат, поэтому его площадь равна стороне квадрата, то есть ребру куба, во второй степени. Площадь боковой поверхности куба состоит из четырех боковых граней-квадратов, а площадь полной поверхности – из шести граней, поэтому для их вычисления нужно умножить площадь одной грани на их количество. Чтобы найти площади куба через радиус сферы, описанной вокруг него, нужно подставить вместо ребра куба удвоенный радиус, деленный на корень из трех. S=a^2=(2R/√3)^2=(4R^2)/3 S_(б.п.)=4S=(16R^2)/3 S_(п.п.)=6S=(24R^2)/3

Объем куба, зная радиус описанной вокруг него сферы, вычисляется возведением в третью степень выражения для ребра куба. V=a^3=(2R/√3)^3=(8R^3)/(3√3)

Периметр куба, как умноженное на 12 ребро куба, представлено через радиус описанной вокруг сферы окружности в виде отношения радиуса, умноженного на 24, к корню из трех. P=12a=24R/√3

Чтобы вычислить радиус сферы, вписанной в куб, через радиус сферы, описанной около него, нужно разделить ребро куба на два, то есть разделить радиус описанной сферы на корень из трех. r=a/2=2R/(2√3)=R/√3

Нахождение радиуса описанной вокруг куба сферы (шара)

В данной публикации мы рассмотрим, чему равняется радиус сферы (шара), описанной около куба, а также как его можно вычислить, если известна длина ребра куба.

Примечание: Напомним, что вокруг любого куба можно описать шар.

Для начала начертим рисунок.

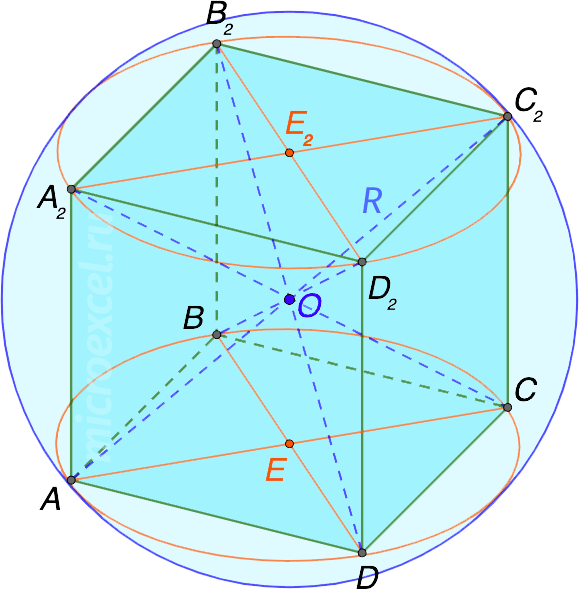
все 8 вершин куба касаются шара – это их общие точки;
центр шара – точка O, которая также является точкой пересечения диагоналей куба.

Радиус шара (R), описанного вокруг куба, равняется половине его диагонали, т.е.:

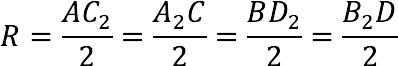
Примечание: все диагонали куба равны.

Чтобы было понятнее, выполним диагональное сечение, т.е. отсечем часть шара вместе со вписанным в него кубом по диагонали куба (линия отреза проходит через точку O).

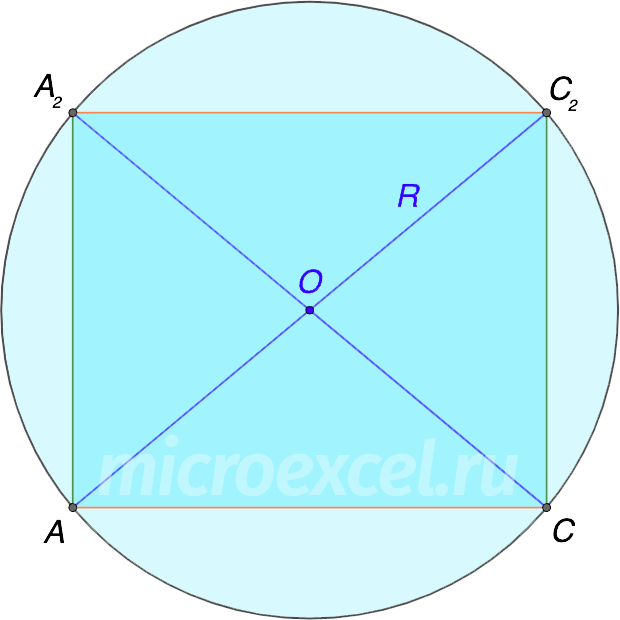
Таким образом, мы получим прямоугольник с описанной вокруг окружностью, радиус которой равняется половине диагонали прямоугольника.

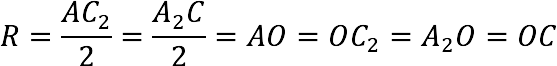
Примечание: Диагонали прямоугольника равны между собой и одновременно являются диагоналями куба.

Формула расчета радиуса описанного шара через ребро куба

Если известна длина ребра куба (примем ее за “a”), радиус описанного вокруг него шара (R) вычисляется следующим образом:

Площадь поверхности вращения при параметрически заданной линии

Если кривая задана параметрическими уравнениями , то площадь поверхности, полученной вращением данной кривой вокруг оси , рассчитывается по формуле . При этом «направление прорисовки» линии, о которое было сломано столько копий в статье Площадь и объем, если линия задана параметрически, безразлично

Но, как и в предыдущем пункте, важно чтобы кривая располагалась выше оси абсцисс – в противном случае функция , «отвечающая за игреки», будет принимать отрицательные значения и перед интегралом придётся поставить знак «минус»

Пример 3

Вычислить площадь сферы, полученной вращением окружности вокруг оси .

Решение: из материалов статьи о площади и объемё при параметрически заданной линии вы знаете, что уравнения задают окружность с центром в начале координат радиуса 3.

Ну а сфера, для тех, кто забыл, – это поверхность шара (или шаровая поверхность).

Придерживаемся наработанной схемы решения. Найдём производные:

Составим и упростим «формульный» корень:

Что и говорить, получилась конфетка. Ознакомьтесь для сравнения, как Фихтенгольц бодался с площадью эллипсоида вращения.

Согласно теоретической ремарке, рассматриваем верхнюю полуокружность. Она «прорисовывается» при изменении значения параметра в пределах (легко видеть, что на данном промежутке), таким образом:

Ответ:

Если решить задачу в общем виде, то получится в точности школьная формула площади сферы , где – её радиус.

Что-то больно простая задачка, даже стыдно стало…. предлагаю вам исправить такую недоработку =)

Пример 4

Вычислить площадь поверхности, полученной вращением первой арки циклоиды вокруг оси .

Задание креативное. Постарайтесь вывести или интуитивно догадаться о формуле вычисления площади поверхности, полученной вращением кривой вокруг оси ординат. И, конечно, снова следует отметить преимущество параметрических уравнений – их не нужно как-то видоизменять; не нужно заморачиваться с нахождением других пределов интегрирования.

График циклоиды можно посмотреть на странице Площадь и объем, если линия задана параметрически. Поверхность вращения будет напоминать… даже не знаю с чем сравнить… что-то неземное – округлой формы с остроконечным углублением посередине. Вот для случая вращения циклоиды вокруг оси ассоциация в голову мгновенно пришла – продолговатый мяч для игры в регби.

Решение и ответ в конце урока.

Завершаем наш увлекательный обзор случаем полярных координат. Да, именно обзор, если вы заглянете в учебники по математическому анализу (Фихтенгольца, Бохана, Пискунова, др. авторов), то сможете раздобыть добрый десяток (а то и заметно больше) стандартных примеров, среди которых вполне возможно найдётся нужная вам задача.

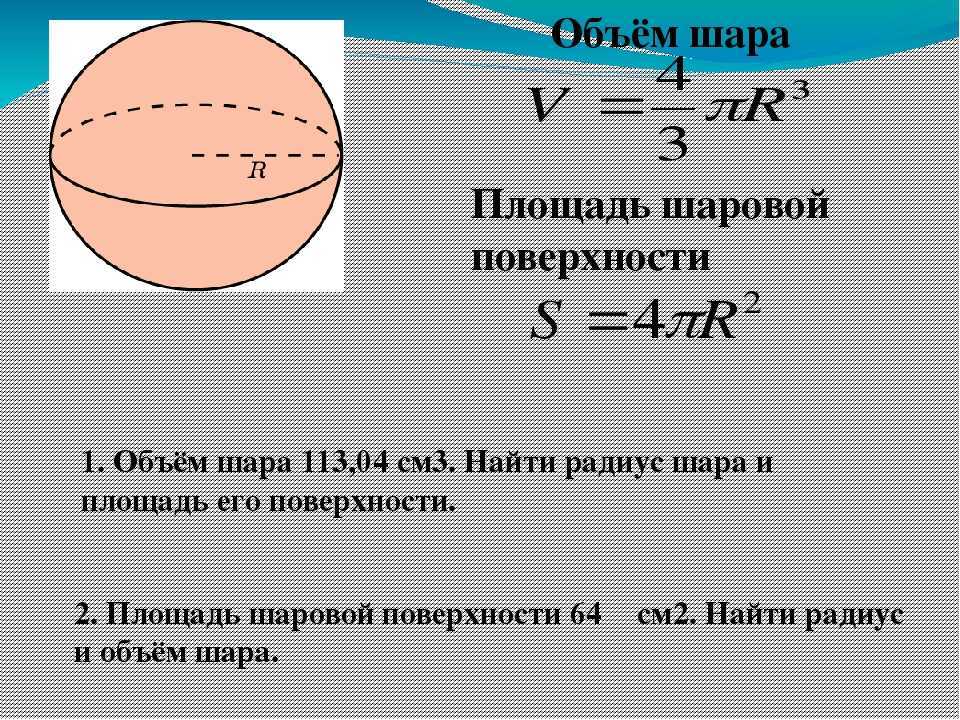
Определение основных величин

1
Запомните основные величины, которые имеют отношение к вычислению радиуса шара. Радиус шара – это отрезок, который соединяет центр шара с любой точкой на его поверхности. Радиус шара можно вычислить по данным значениям диаметра, длины окружности, объема или площади поверхности. Диаметр (D) – это отрезок, который соединяет две точки на поверхности шара и проходит через его центр (то есть это наибольшее расстояние между противоположными точками, лежащими на поверхности шара). Диаметр равен удвоенному радиусу. Длина окружности (С) представляет собой длину окружности большого круга, то есть круга, который образует секущая плоскость, проходящая через центр шара. Объем (V) – это значение трехмерного пространства, занимаемого шаром. Площадь поверхности (А) – это значение двумерного (плоского) пространства, ограниченного поверхностью шара. Пи (π) – это постоянная, которая равна отношению длины окружности к ее диаметру. Первыми десятью цифрами этой постоянной являются 3,141592653, но зачастую число Пи округляется до 3,14.
2
Воспользуйтесь значениями данных величин, чтобы найти радиус. Радиус можно вычислить по данным значениям диаметра, длины окружности, объема и площади поверхности. Более того, указанные величины можно найти по данному значению радиуса. Чтобы вычислить радиус, просто преобразуйте формулы для нахождения указанных величин. Ниже приведены формулы (в которых присутствует радиус) для вычисления диаметра, длины окружности, объема и площади поверхности. D = 2г. Как и в случае круга , диаметр шара в два раза больше его радиуса. C = πD = 2πr. Как и в случае круга , длина окружности шара равна произведению π на диаметр шара. Так как диаметр вдвое больше радиуса, то длина окружности шара равна удвоенному произведению π на радиус шара. V = (4/3)πr3. Объем шара равен произведению 4/3 на π и на радиус в кубе. А = 4πr2. Площадь поверхности шара равна учетверенному произведению π на радиус в квадрате. Так как площадь круга равна πr2, то площадь поверхности шара в четыре раза больше площади круга, который образует секущая плоскость, проходящая через центр шара.