Квадрат суммы и квадрат разности, разность квадратов

Квадрат разности

Для доказательства справедливости формулы квадрата разности достаточно перемножить выражения раскрыв скобки:

( a — b ) 2 = ( a — b )·( a — b ) = a 2 — ab — ba + b 2 = a 2 — 2 ab + b 2

Применение формулы квадрата разности

для раскрытия скобок
для упрощения выражений
для вычисления квадратов больших чисел, не используя калькулятор или умножение в столбик

Примеры задач на применение формулы квадрата разности

( x — 3) 2 = x 2 — 2·3· x + 3 2 = x 2 — 6 x + 9

(2 x — 3 y 2 ) 2 = (2 x ) 2 — 2·(2 x )·(3 y 2 ) + (3 y 2 ) 2 = 4 x 2 — 12 x y 2 + 9 y 4

Можно заметить, что выражение в числителе — это разложенный квадрат разности

9 x 2 — 6 x + 1 (3 x — 1) = (3 x — 1) 2 (3 x — 1) = 3 x — 1

69 2 = (70 — 1) 2 = 70 2 — 2·70·1 + 1 2 = 4900 — 140 + 1 = 4761

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool. Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Доказательство формулы

Арифметическое

Представим формулу в виде произведения двух одинаковых скобок (другими словами, умножим выражение само на себя):
(а+б)(а+б).

Теперь раскроем скобки по правилам арифметики и получим:
(a+b)(a+b) = a2 + ab + ba + b2 = a2 + 2ab + b2.

Геометрическое

Чтобы доказать формулу геометрически, начертим квадрат, который разделен двумя отрезками на четыре части таким образом, что получим:

два квадрата с разной длиной сторон (а или б);
2 прямоугольника одинаковой длины (а) и ширины (б).

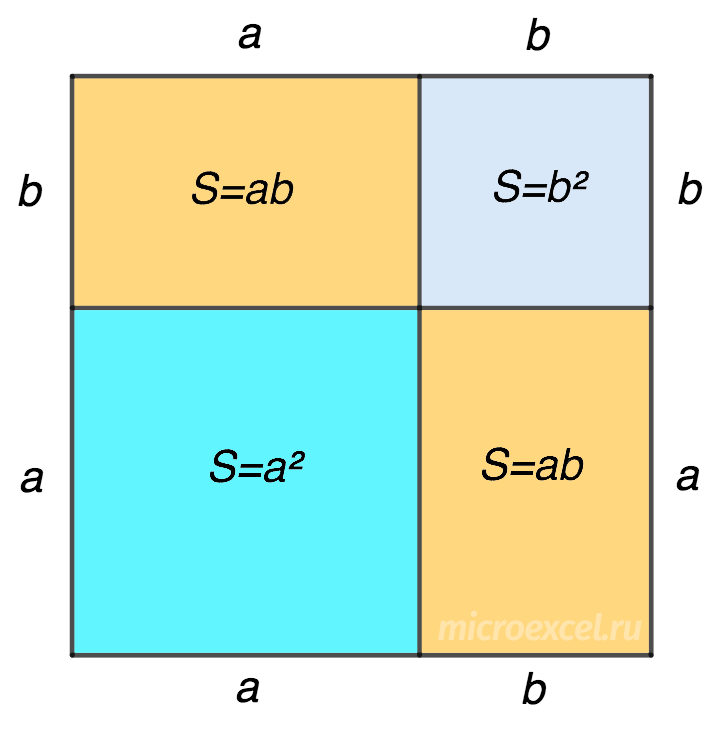
Площадь большого квадрата равна (а+b)2 и одновременно сумме площадей фигур, составляющих:

Кв. = (a + b)2 = a2 + ab + ab + b2 = a2 + 2ab + b2.

Формула квадрата суммы и неполного квадрата суммы

Также легко, как и в предыдущем случае, выводится эта формула:

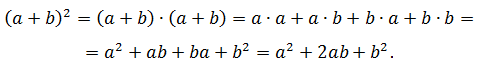
Квадрат суммы двух выражений равен сумме квадратов каждого из них плюс их удвоенное произведение:

Многие школьники, начинающие знакомиться с этим материалом, часто теряют двойку во втором слагаемом правой части, получая

Однако, в этом случае, возникает неполный квадрат суммы (или разности), который на множестве действительных чисел не раскладывается на множители.

Обе формулы применяются не только для раскрытия скобок, но и для разложения на множители, что в свою очередь упрощает приведение к одному знаменателю, сокращение дробей, решение уравнений высоких степеней.

Доказательство формулы

Арифметическое

Давайте проверим формулу от обратного, т.е. перемножим (a-b) и (a+b) .

Раскрыв скобки с учетом правил арифметики получаем исходную формулу: (a-b)(a+b) = a 2 + ab – ba – b 2 = a 2 – b 2 .

Геометрическое

Изобразим квадрат с длиной стороны a , площадь которого равна a 2 . В нем расположен квадрат поменьше со стороной b и площадью b 2 .

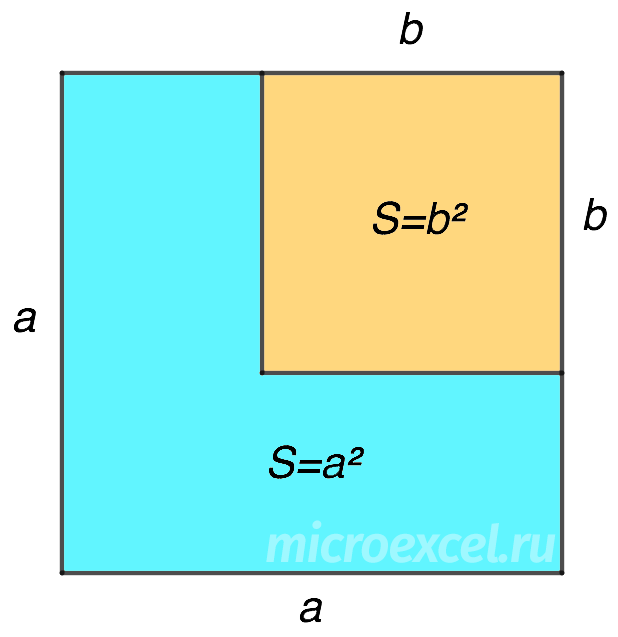
Задача состоит в том, чтобы найти площадь фигуры голубого цвета ( a 2 – b 2 ).

Продолжив любую из линий сторон меньшего квадрата до границ большего мы получим:

квадрат площадью b 2 ;
прямоугольник со сторонами a и ( a-b );
прямоугольник со сторонами b и ( a-b ).

Нам нужна только сумма площадей прямоугольников, которая вычисляется таким образом:

S = a ⋅ (a – b) + b ⋅ (a – b) = a 2 – ab + ba – b 2 = a 2 – b 2

Квадрат суммы

\( \displaystyle {{(a+b)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\)

Название «Формулы сокращенного умножения» совсем не случайно, потому что эти формулы позволяют сократить время на умножение. Вот смотри…

Возьмем самую простую первую формулу квадрата суммы \( {{\left( a+b \right)}^{2}}\) — и попробуем возвести сумму в скобках в квадрат, то есть, умножить \( \left( a+b \right)\) само на себя:

Приведи подобные слагаемые и ты получишь формулу сокращенного умножения квадрат суммы:

Таким образом выводятся все формулы сокращенного умножения.

Ты можешь выводить их каждый раз самостоятельно, а можешь не тратить на это время и быстро посчитать необходимый пример, зная конечное значение формул.

Конечно, квадрат суммы посчитать вручную не так сложно, но что ты скажешь насчет куба суммы или куба разности?

Куб суммы означает, что необходимо \( \left( a+b \right)\) само умножить на себя три раза:

И это мы расписали перемножение только первой скобки, а тоже самое необходимо сделать со второй и с третьей… Согласись, запутаться очень легко, а, как правило, от того, как ты посчитаешь это простое действие, зависит ответ всего примера.

Таким образом, формулы сокращенного умножения позволяют сократить трудоемкое перемножение членов друг на друга и получить быстрый результат.

Квадрат суммы и разности двух чисел

Рассмотрим формулы 1 и 2. Их можно объединить следующим образом:

(a \pm b)^2=a^2 \pm 2ab +b^2

Читается так:

Квадрат суммы (разности) двух чисел

Квадрат суммы (соответственно разности) двух чисел равен квадрату первого числа, плюс (минус) удвоенное произведение первого числа на второе, плюс квадрат второго числа.(a \pm b)^2=a^2 \pm 2ab +b^2

Примеры на квадрат суммы и разности двух чисел

Выполнить действия

(x+2y)^2(x+2y)^2=x^2+2x (2y)+y^2=x^2+4xy+4y^2
(m+n^2)^2(m+n^2)^2=m^2+2mn^2+n^4
(m+n^2)^2(a^2+b^4)^2=a^4+2a^2b^4+b^8

Представить в виде квадрата двучлена следующие трехчлены.

x^2+2x+1x^2+2x+1=(x+1)^2
4a^2+4ab+b^24a^2+4ab+b^2=(2a)^2+2\cdot (2a)\cdot b+b^2=(2a+b)^2
m^6+2m^3n^4+n^8(m^3)^2+2 (m^3)(n^4)+(n^4)^2=(m^3+n^4)^2

Дополнить до полного квадрата двучлена следующие выражения:

4a^2+12ab+… Чтобы найти третье слагаемое — ориентируемся на второе слагаемое в котором выделяем корень квадратный из первого. То есть, второе слагаемое 12ab из него выделяем корень квадратный из первого слагаемого \sqrt{4a^2}=2a, остается 12ab :2a=6b. Но так как в формуле (a+b)^2=a^2+2ab+b^2 и во втором слагаемом мы видим удвоенное произведение первого слагаемого на второе, нужно еще разделить на 2. Первое слагаемое мы определили, это 2a, теперь от 6b убираем множитель 2 и остается третье слагаемое 3b. И мы получаем: 4a^2+12ab+…=(2a)^2+2\cdot (2a)\cdot (3b)+(3b)^2=4a^2+12ab+9b^2m^2-2mn+…
m^2-2 \cdot m \cdot n+…=m^2-2\cdot m\cdot n+n^2
25x^2+ ? + 49b^225x^2+ ? + 49b^2=(5x)^2+?+(7b^2)=(5x)^2+2 (5x)(7b)+(7b)^2=25x^2+70xb+49b^2

Выделить квадрат суммы или разности:

x^2+8xНам дан неполный квадрат суммы. Дополняя мы обычно либо выделяем какое то число или выражение, если нам не хватает до полного квадрата суммы или разности, или добавляем его, но тогда то же выражение надо и отнять.x^2+8x=x^2+2\cdot 4 \cdot x+(4)^2- (4)^2=(x+4)^2-16
x^2-2x+3x^2-2x+3=x^2-2x+1+2=(x-1)^2+2
x^2+6x-3x^2+6x-3=(x)^2+2 \cdot x \cdot 3+9-9-3=(x)^2+6x+9-12=(x+3)^2-12

Вычислите, используя формулы (a+b)^2=a^2+2ab+b^2 и (a-b)^2=a^2-2ab+b^2:

103^2103^2=(100+3)^2=100^2+2\cdot 100 \cdot 3+3^2=10000+600+9=10609
49^249^2=(50-1)^2=50^2-2\cdot 50\cdot 1+1^2=2500-100+1=2401
10,5^210,5^2=(10+0,5)^2=10^2+2\cdot 10 \cdot 0,5+0,5^2=100+10+0,25=110,25
99^299^2=(100-1)^2=100^2-2\cdot 100 \cdot 1+1=10000-200+1=9801
8,9^28,9^2=(9-0,1)^2=9^2-2\cdot 9 \cdot 0,1+0,1^2=81-1,8+0,01=79,2+0,01=79,21

Задания для самостоятельного решения

Задание 1. Преобразуйте выражение (m + n)2 в многочлен.

Решение:
(m + n)2 = m2 + 2mn + n2

Задание 2. Преобразуйте выражение (x + 8)2 в многочлен.

Решение:
(x + 8)2 = x2 + 2 × x × 8 + 82 = x2 + 16x + 64

Задание 3. Преобразуйте выражение (2×2 + 3×3)2 в многочлен.

Решение:
(2×2 + 3×3)2 = (2×2)2 + 2 × 2×2 × 3×3 + (3×3)2 = 4×4 + 12×5 + 9×6

Задание 4. Преобразуйте выражение (5a + 5)2 в многочлен.

Решение:
(5a + 5)2 = (5a)2 + 2 × 5a × 5 + 52 = 25a2 + 50a + 25

Задание 5. Преобразуйте выражение (9 − x)2 в многочлен.

Решение:
(9 − x)2 = 92 − 2 × 9 × x + x2 = 81 − 18x + x2

Задание 6. Преобразуйте выражение (x − 25)2 в многочлен.

Решение:
(x − 25)2 = x2 − 2 × x × 25 + 252 = x2 − 50x + 625

Задание 7. Преобразуйте выражение (3×2 − y3)2 в многочлен.

Решение:
(3×2 − y3)2 = (3×2)2 − 2 × 3×2 × y3 + ( y3)2 = 9×4 − 6x2y3 + y6

Задание 8. Выполните умножение (x − y)(x + y)

Решение:
(x − y)(x + y) = x2 − y2

Задание 9. Выполните умножение (2x − y)(2x + y)

Решение:
(2x − y)(2x + y) = (2x)2 − y2 = 4×2 − y2

Задание 10. Выполните умножение (7 + 3y)(3y − 7)

Решение:
(7 + 3y)(3y − 7) = (3y)2 − 72 = 9y2 − 49

Задание 11. Выполните умножение (x2 − 5)(x2 + 5)

Решение:
(x2 − 5)(x2 + 5) = (x2)2 − 52 = x4 − 25

Задание 12. Выполните умножение (a3 − b2)(a3 + b2)

Решение:
(a3 − b2)(a3 + b2) = (a3)2 − (b2)2 = a6 − b4

Задание 13. Выполните умножение (5a2 + 2b3)(5a2 − 2b3)

Решение:
(5a2 + 2b3)(5a2 − 2b3) = (5a2)2 − (2b3)2 = 25a4 − 4b6

Задание 14. Выполните умножение (9x − y2)(y2 + 9x)

Решение:
(9x − y2)(y2 + 9x) = (9x)2 − (y2)2 = 81×2 − y4

Задание 15. Выполните умножение (2 − x)(4 + 2x + x2)

Решение:
(2 − x)(4 + 2x + x2) = 23 − x3 = 8 − x3

Задание 16. Выполните умножение (3 − 2)(9 + 6 + 4)

Решение:
(3 − 2)(9 + 6 + 4) = 33 − 23 = 27 − 8 = 19

Задание 17. Выполните умножение (4x + 1)(16×2 − 4x + 1)

Решение:
(4x + 1)(16×2 − 4x + 1) = (4x)3 + 13 = 64×3 + 1

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Разложение квадратного трёхчлена на множители

Утверждение. В случае, когда , квадратный трёхчлен (1) разлагается на линейные множители. В случае, когда D < 0, квадратный трехчлен нельзя разложить на линейные множители.

Доказательство. В случае, когда D = 0, формула (8) и является разложением квадратного трехчлена на линейные множители:

(9)

В случае, когда D > 0, выражение, стоящее в квадратных скобках в формуле (8), можно разложить на множители, воспользовавшись :

Таким образом, в случае, когда D > 0, разложение квадратного трехчлена (1) на линейные множители имеет вид

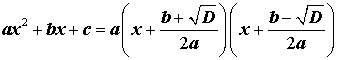(10)

В случае, когда D < 0, выражение, стоящее в квадратных скобках в формуле (8), является суммой квадратов и квадратный трёхчлен на множители не раскладывается.

Замечание. В случае, когда D < 0, квадратный трехчлен всё-таки , однако этот материал выходит за рамки школьного курса.

Фсу – формулы сокращённого умножения по алгебре за 7 класс с примерами

Основная задача формул сокращённого умножения

Формулы сокращённого умножения (ФСУ) нужны для того, чтобы умножать и возводить в степень числа, выражения, в том числе многочлены. То есть, при помощи формул можно работать с числами значительно быстрее и проще. Таким образом можно из сложного уравнения сделать обычное, что упростит задачу.

Таблица с формулами сокращённого умножения

Квадрат суммы		Квадрат первого выражения плюс удвоенного произведение первого и второго выражения, плюс квадрат второго выражения.
Квадрат разности		Квадрат разности двух выражений равен квадрату первого выражения, минус удвоенное произведение первого выражения на второе, плюс квадрат второго выражения.
Куб суммы		Куб разности двух выражений равен кубу первого выражения плюс утроенное произведение первого выражения в квадрате на второе выражение, плюс утроенное произведение первого выражения на второе в квадрате, плюс второе выражение в кубе.
Куб разности		Куб разности двух величин равен первое выражение в кубе минус утроенное произведение первого выражения в квадрате на второе выражение, плюс утроенное произведение первого выражения на второе в квадрате, минус второе выражение в кубе.
Разность квадратов		Разность квадратов первого и второго выражений равен произведению разности двух выражений и их суммы.
Сумма кубов		Произведение суммы двух величин на неполный квадрат разности равно сумме их кубов.
Разность кубов		Произведение разности двух выражений на неполный квадрат суммы равно разности их кубов.

Формулы сокращенного умножения (скачать таблицу для печати)

Обратите внимание на первые четыре формулы. Благодаря им можно возводить в квадрат или куб суммы (разности) двух выражений

Что касается пятой формулы, её нужно применять, чтобы вкратце умножить разность или сумму двух выражений.

Две последние формулы (6 и 7) применяются, чтобы умножать суммы обоих выражений на их неполный квадрат разности или суммы.

Вышеперечисленные формулы довольно-таки часто нужны на практике. Именно поэтому их желательно знать наизусть.

Такую же процедуру можно проделывать и с остальными формулами.

Доказательство ФСУ

Шаг первый.

Возведём a + b во вторую степень. Для этого степень трогать не будем, а выполним банальное умножение: = x .

Шаг второй. Теперь и выносим за скобки: x + x .

Шаг третий. Раскрываем скобки: x + x + x + x .

Шаг четвёртый. Умножаем, не забывая о знаках: x + x + .

Шаг пятый. Упрощаем выражение: .

Точно так же можно доказать абсолютно любую формулу сокращённого умножения.

Примеры и решения с помощью ФСУ

Как правило, эти семь формул применяются тогда, когда нужно упростить выражение, чтобы решить какое-либо уравнение и даже обычный пример.

Пример 1

Задание
Упростите выражение:
Как видно, к этому примеру подходит первая формула сокращённого умножения – Квадрат суммы.
Решение

Исходя из первой формулы надо пример разложить на множители. Для этого смотрим на формулу и вместо букв подставляем цифры. В нашем случае «а» – это 3x, а «b» – это 5:

x x +
Считаем правую часть и записываем результат. У нас получается:
+ x x +
В примере надо умножить всё то, что умножается и сразу получаем ответ:

Конечно же, есть примеры и с дробями. Но, если научитесь решать простые примеры, тогда другие виды вам будут не страшны.

Пример 2

Задание
Упростите выражение
Решение
= – x x + =

Пример 3

Задание
Представьте в виде квадрата двучлена трёхчлен
Решение
Здесь квадраты выражений – и
Выражения, которые возводились в квадрат – и
Удвоенное произведение этих выражений – , который совпадает с со вторым членом трёхчлена (со знаком «плюс), значит,

Итак, как видно, ничего сложно в примерах нет. Главное, знать формулы, где их можно применять, а где можно обойтись и без них.

Полезные источники

Арефьева И. Г., Пирютко О. Н. Алгебра: учебник пособие для 7 класса учреждений общего среднего образования: Минск “Народная Асвета”, 2017 – 304 с.
Никольский С. М., Потапов М. К. Алгебра 7 класс: М: 2015 – 287 с.
Рубин А. Г., Чулков П. В. Алгебра. 7 класс. М: 2015 – 224 с.

Примеры задач с решением

Задача №3

Преобразовать трёхчлен в квадрат двучлена:

28xy + 49×2 + 4y2

Решение.

Поскольку квадраты находятся на втором и третьем местах, поменяем слагаемые между собой и подготовим выражение для применения формулы:

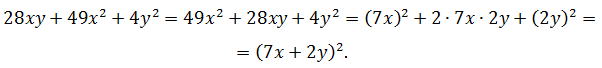
Ответ: (7x + 2y)2.

Возведение во вторую степень суммы трёх и более слагаемых выполняется аналогично: необходимо возвести в квадрат каждый элемент, записать все возможные удвоенные произведения и сложить полученные результаты.

Правила возведения в степени более высоких порядков возникают, когда выполняется умножение одинаковых многочленов несколько раз.

Возможность выполнять возведение в квадрат больших чисел, не используя калькулятор, является одним из преимуществ сокращённого умножения.

Выполнить раскрытие скобок и упростить:

(x2 + 3x — 4y)2 — x4 — 9×2 — 16y2

Решение.

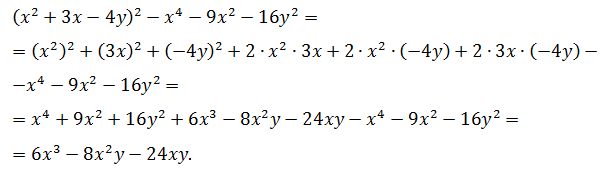
Ответ: 6×3 — 8×2 — 24xy.

Задача №5

Вычислить:

1032 + 1972

Решение.

Для каждого слагаемого применяется одно из правил возведения в квадрат, затем производится суммирование результатов:

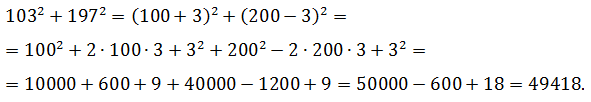
Решая квадратные уравнения, вместо поиска дискриминанта выделяют полный (точный) квадрат среди слагаемых, расположенных в левой части. В правую сторону собираются оставшиеся элементы.

Задача №6

Решить уравнение:

x2 — 4x — 5 = 0

Решение.

Первые два слагаемых левой части полностью удовлетворяют формуле квадрата суммы. Соотнеся их с соответствующими элементами правила, определяют, прибавляют и вычитают третье, затем сворачивают в точный квадрат, остальные члены алгебраической суммы переносят в правую сторону:

Решениями исходного уравнения являются корни уравнений

Ответ: x = 5 или x = -1.

Выделение полного квадрата

Часто в многочлене второй степени содержится квадрат суммы или разности, но
содержится в скрытом виде. Чтобы получить полный квадрат в явном виде, нужно преобразовать
многочлен. Для этого, как правило, одно из слагаемых многочлена представляется в виде удвоенного
произведения, а затем к многочлену прибавляется и из него вычитается одно и то же число.

Пример 7. Рассмотрим многочлен второй степени

Решение. Этот многочлен можно преобразовать следующим образом:

Здесь мы представили
в виде удвоенного произведения на ,
прибавили к многочлену и вычли из него одно и то же число
, далее применили
формулу квадрата суммы для двучлена .

Итак, мы доказали равенство

показывающее, что многочлен второй степени

равен полному квадрату
плюс число .

Пример 8. Рассмотрим многочлен второй степени

Решение. Проведём над ним следующие преобразования:

Здесь мы представили
в виде удвоенного произведения на ,
прибавили к многочлену и вычли из него одно и то же число
, применили
формулу квадрата разности для двучлена .

Итак, мы доказали равенство

показывающее, что многочлен второй степени

равен полному квадрату
плюс число .

Прямая и обратная теоремы Виета

Раскрывая скобки и приводя подобные члены в правой части формулы (17), получаем равенство

ax2 + bx + c == a (x – x₁) (x – x₂) == a [x2 – (x₁ + x₂) x + x₁x₂] == ax2 – a(x₁ + x₂) x + ax₁x₂ .

Отсюда, поскольку формула (17) является тождеством, вытекает, что коэффициенты многочлена

ax2 + bx + c

равны соответствующим коэффициентам многочлена

ax2 – a (x₁ + x₂) x + a x₁x₂ .

Таким образом, справедливы равенства

следствием которых являются формулы

(18)

Формулы (18) и составляют содержание теоремы Виета (прямой теоремы Виета).

Словами прямая теорема Виета формулируется так: — «Если числа x₁ и x₂ являются корнями квадратного уравнения (1), то они удовлетворяют равенствам (18)».

Обратная теорема Виета формулируется так: — «Если числа x₁ и x₂ являются решениями системы уравнений (18), то они являются корнями квадратного уравнения (1)».

Для желающих ознакомиться с примерами решений различных задач по теме «Квадратные уравнения» мы рекомендуем наше учебное пособие «Квадратный трехчлен».

Графики парабол и решение с их помощью квадратных неравенств представлены в разделе «Парабола на координатной плоскости. Решение квадратных неравенств» нашего справочника.