Деление десятичной дроби на натуральное число

Деление десятичной дроби на другую десятичную дробь

Теперь разберём случай, когда делимое тоже является дробью.

Отрезок EF равен $1.3$ см, а отрезок GH равен $3.9$ см. Во сколько раз отрезок GH больше?

Напрашивается то же самое решение: переводим оба размера в миллиметры, то есть умножаем на $10$. Теперь мы можем разделить $39$ на $13$, у нас получится $3$. Можно даже проверить при помощи линейки – деление выполнено верно.

Рисунок 4

Получается, действуем по тому же алгоритму: умножаем делимое и делитель на одно и то же разрядное число, добиваясь, чтобы делитель стал натуральным числом.

{"questions":}},"step":1,"hints":["Высчитаем частное в каждом примере. Для этого превратим делитель из десятичной дроби в натуральное число. Так как количество знаков после запятой в делимых и делителях одинаковы, в каждом примере можно просто убрать запятые.","$4.8 : 0.6 = 48 : 6 = 8$<br />$6.3 : 0.9 = 63 : 9 = 7$<br />$4.2 : 0.7 = 42 : 7 = 6$"]}]}

Работа с округленными числами

Округление уже округленных чисел

Если исходное число уже является результатом округления, то для пограничного случая, когда новая цифра округления равна 5 (и все цифры после этого нуля), по возможности следует использовать неокругленное число (например, с математическими константами):

Известное неокругленное число: 13.374999747, округленное начальное число: 13.3750

→ Округление неокругленного числа до двух десятичных знаков дает: 13,37

Неокругленное число неизвестно, начальное число округлено: 13.3750

→ Округление ранее округленного числа до двух десятичных знаков дает: 13,38.

Идентификация результатов округления

В научных статьях и таблицах логарифмов иногда указывается, была ли последняя цифра получена округлением в большую или меньшую сторону. Число, полученное округлением в большую сторону, обозначается линией под (или над) числом, число, которое не было изменено округлением (число было округлено), отмечается точкой над числом.

Примеры:

• 3,4134928 …{ displaystyle 3 {,} 4134928 …}становится к ; это число – новые раунды . При повторном округлении (в примере до трех знаков после запятой) его необходимо округлить в меньшую сторону.3,4135_{ displaystyle 3 {,} 413 { underline {5}}}3,413{ displaystyle 3 {,} 413}
• 2,6245241 …{ displaystyle 2 {,} 6245241 …}становится к ; это число станет яснее при следующем округлении до . При повторном округлении (в примере до трех знаков после десятичной точки) вам необходимо округлить в большую сторону. Для дальнейшего округления (здесь до двух мест) оно будет округлено в меньшую сторону, обозначенное цифрой 5 .2,6245˙{ displaystyle 2 {,} 624 { dot {5}}}2,625{ displaystyle 2 {,} 625}2,625_{ displaystyle 2 {,} 62 { underline {5}}}

Если другие цифры не известны, предполагается, что начальный номер является точным.

Расчет с округленными числами

Если в расчет включены округленные числа, окончательный результат должен быть округлен до того же количества значащих цифр. Если z. Например, если измеряется сила в 12,2 Ньютона, все окончательные результаты, зависящие от этой силы, должны быть округлены так, чтобы осталось не более трех значащих цифр. Таким образом, читатель не претендует на то, чтобы быть более точным, чем то, что на самом деле доступно.

Что делать с целой частью

На самом деле всё очень просто: если мы хотим получить правильную дробь, то необходимо убрать из неё целую часть на время преобразований, а затем, когда получим результат, вновь дописать её справа перед дробной чертой.

Например, рассмотрим то же самое число: 1,88. Забьём на единицу (целую часть) и посмотрим на дробь 0,88. Она легко преобразуется:

Затем вспоминаем про «утерянную» единицу и дописываем её спереди:

\

Вот и всё! Ответ получился тем же самым, что и после выделения целой части в прошлый раз. Ещё парочка примеров:

\

В этом и состоит прелесть математики: каким бы путём вы не пошли, если все вычисления выполнены правильно, ответ всегда будет одним и тем же.:)

В заключение хотел бы рассмотреть ещё один приём, который многим помогает.

Алгоритм Евклида для вычисления НОД (наибольшего общего делителя)

Не всегда, сходу, можно понять какое число является наибольшим общим числителем, особенно если числа крупные, поэтому существует специальный алгоритм для выведения такого числа НОД.

Суть алгоритма такова: для нахождения НОД чисел а и b (где они целые и положительные числа, к тому же a больше b), выполняется ряд делений с остатком, получается ряд равенств, где деление останавливается в том случае если r_k+1=0, при этом r_k=НОД(a, b)

Пример. Рассчитаем НОД для 28 и 64.

Как находим:

Распишем простые множители для каждого числа и подчеркнем одинаковые

Д (28) = 2 * 2 * 7

Д (64) = 2 * 2 * 2 * 2 * 2 * 2

Найдем произведение одинаковых простых множителей и запишем ответ

НОД (28; 64) = 2 * 2 = 4

Ответ: НОД (28; 64) = 4

Оформить поиск НОД можно в строчку, как мы сделали выше или в столбик, как на картинке.

Представление десятичной дроби в виде обыкновенной и обыкновенной в виде десятичной

Чтобы обратить десятичную дробь в обыкновенную, достаточно в числителе дроби записать число, стоящее после запятой, а в знаменателе — единицу с нулями, причем нулей должно быть столько, сколько цифр справа от запятой. Если можно, дробь сократить.

Чтобы обратить обыкновенную дробь в десятичную, следует разделить числитель на знаменатель по правилу деления десятичной дроби на целое число.

Не каждую обыкновенную дробь можно перевести в десятичную. Если знаменатель обыкновенной дроби не содержит простых множителей, кроме 2 и 5, то эту обыкновенную дробь можно перевести в десятичную.

Учитывая это правило, можно переводить обыкновенную дробь в десятичную не с помощью деления, а приведением ее к знаменателю 10, 100, 1000 путем умножения числителя и знаменателя этой дроби на недостающие множители.

Это конспект по теме «Десятичная дробь». Выберите дальнейшие действия:

• Перейти к следующему конспекту: 
• Вернуться к списку конспектов по Математике.
• Проверить знания по Математике.

Преобразование десятичных дробей

Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!

Как перевести десятичную дробь в проценты

Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.

Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.

А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:

0,15 = 0,15 · 100% = 15%.

Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.

2/5 = 0,4 0,4 · 100% = 40%

8/25 = 0,32 0,32 · 100% = 32%

Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:

Преобразование десятичных дробей

Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.

Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).

Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!

Пример 1. Перевести 5,4 в смешанное число.

1. Читаем вслух: пять целых четыре десятых. «Четыре десятых» подсказывают, что в числителе будет 4, а в знаменателе — 10. В смешанном виде эта дробь выглядит так: 5 4/10.
2. А теперь сократим числитель и знаменатель на два (потому что можно) и получим: 5 2/5.

Пример 2. Перевести 4,005 в смешанное число.

1. Читаем вслух: четыре целых пять тысячных. Значит 5 — идет в числитель, а 1000 — в знаменатель. В смешанном виде получается так: 4 5/1000. После сокращения: 4 1/200.

Ответ: 4,005 = 4 1/200.

Пример 3. Перевести 5,60 в смешанное число.

1. Читаем вслух: пять целых шестьдесят сотых. Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
2. Сократим дробную часть на 10 и получим 5 6/10. Или можно вспомнить про свойство десятичной дроби и просто отбросить нули в числителе и знаменателе.

Ответ: 5,60 = 5 6/10.

Как перевести десятичную дробь в обыкновенную

Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:

1. Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу. Например:
   • 0,35 = 0,35/1
   • 2,34 = 2,34/1
2. Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
   • 0,35 = 0,35/1 = 3,5/10 = 35/100
   • 2,34 = 2,34/1 = 23,4/10 = 234/100
3. А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
   • 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
   • 2,34 = 234/100 = 117/50 = 2 17/50.

Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!

Что такое дробь, основные понятия и виды

Определение

Дробь — число, состоящее из нескольких равных долей.

По сути дробь — это деление одного числа на другое. Выделяют два вида: обыкновенные и десятичные.

Обыкновенная дробь — означает, состоящая из целых чисел. Обыкновенные, имею два типа записи к примеру:

• 15- разделена наклонной линией, читается как одна пятая;
• — горизонтальной линией.

Определения:

• Числитель — число, находящееся в верхней границе дроби;
• Знаменатель — число которое мы видим в нижней границе дроби.

Например: 15, где 1- числитель, 5- знаменатель. Для того чтобы проще объяснить, что такое дробь приведём простой пример. Торт разрезан на 5 кусков, если мы взяли два и них то это 25 (две пятые части торта).

Обыкновенные дроби имеют два типа правильные и неправильные.

Правильной дробью называется дробь с значениями, в которых числитель меньше знаменателя. Такое название данный тип дроби получил не зря, ведь так логичнее и правильнее, когда часть меньше целого.

Неправильная в свою очередь имеет обратные значения, когда числитель больше знаменателя.

_{Примечание. Дроби, у которых знаменатель и числитель одинаковы, тоже неправильные.}

Смешанная дробь. Существует также такое определение как смешанная дробь, такой вид, представляет собой дробь, состоящую из двух частей целой и дробной. Пример — , где четыре это целая часть, а 35 дробная. Такой тип дроби можно получить, только при делении неправильного вида дробей.

Десятичные дроби. К десятичным, относят дроби которые в знаменателе имеют 10 в натуральной степени. К примеру и тд. Такие, так же могут иметь вид строчной записи, 0,5 и 0,06. При этом в такой записи целая часть отделяется от дробной знаком запятой.

Существуют также понятия сократимой и несократимой дроби. Сократимая дробь, это та, в которой можно произвести деление числителя и знаменателя на одно и то же число.

Несократимая дробь, если такие действия выполнить нельзя.

Составная дробь, многоуровневая или выражение, имеющее несколько черт дроби. Пример

Равные и неравные дроби. Для того чтобы сказать, являются дроби равными или нет, нужно их сравнить.

Равные обыкновенные — можно вывести при помощи такого верного равенства а*b=d*c , если такое равенство не верно то данные дроби будут называться неравными.

Положительные и отрицательные дроби.

Положительные называют обыкновенные дроби, с положительными числами, при необходимость перед такими дробями ставится знак +, пример .

Отрицательными, считаются дроби со знаком минус, пример .

Стоит отметить что две дроби вида являются противоположными.

Алгебраическая дробь.

Отличается она тем, что на месте числителя и знаменателя находятся алгебраические значения, числа заменены буквами. Примеры —

Если в такой дроби буквы заменить числами, то она сразу станет обыкновенной.

Одночлен — это выражение, содержащее числа, степени положительные и их произведение. Пример:

Многочлен — это сумма одночленов. Пример: 7а+6в

Дроби на координате прямых.

Если рассматривать координату прямых, то положительные дроби на ней будут расположены справа от нулевого значения, а отрицательные слева.

Основы деления десятичных дробей

Все десятичные дроби, будь то конечные или периодические, являются лишь особой формой дробей. Поэтому к ним применяются те же принципы, что и к их обычным аналогам. Таким образом, мы сводим весь процесс деления десятичных чисел к обыкновенной дроби, а затем вычисляем с помощью уже известных нам средств. Давайте рассмотрим конкретный пример.

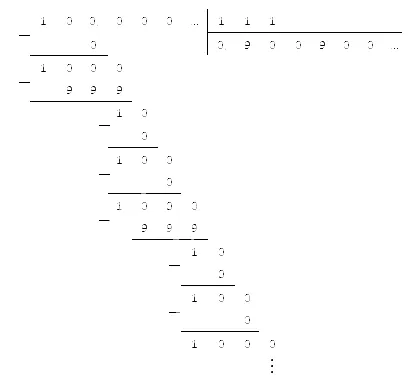
Однако, когда мы сталкиваемся с непериодическими десятичными числами в примере деления, мы действуем немного иначе. Мы не можем разделить их на обычные дроби, поэтому при делении их нужно сначала округлить до определенной цифры. Это необходимо сделать как с делителем, так и с делимым: существующая конечная или периодическая дробь также округляется для обеспечения точности.

Выводы

В данной статье мы рассмотрели основные методы и правила для перевода десятичных дробей в целые числа, выполнения операций с дробями и перевода дробей в проценты. Мы также рассмотрели способ деления десятичных дробей на натуральные числа столбиком. Ознакомившись с этой информацией и усвоив правила, можно успешно выполнять подобные математические операции без труда.

Куда нужно сдвинуть запятую Чтобы разделить десятичную дробь

Чтобы разделить десятичную дробь, нужно сдвинуть запятую вправо на столько цифр, сколько цифр насчитывается в делителе. Для этого применяется правило деления на десятичную дробь. Например, если у нас есть число 3,25 и мы хотим разделить его на 0,5, то запятую нужно сдвинуть вправо на одну цифру. Получится 32,5. Затем выполняется деление на натуральное число, то есть число без запятой. В данном случае 32,5 разделим на 5 и получим результат 6,5. Таким образом, мы разделили десятичную дробь на другую десятичную дробь. Используя указанное правило, можно сдвигать запятую и выполнять деление на различные десятичные дроби.

Как число перевести в обыкновенную дробь

Например, если у нас есть число 5, мы умножаем его на знаменатель, который может быть произвольным числом, и прибавляем числитель — может быть также произвольным числом. Полученная дробь будет неправильной, так как числитель больше знаменателя. Но если мы хотим получить обыкновенную дробь, то нужно упростить ее. Для этого находим наибольший общий делитель числителя и знаменателя и делим оба числа на него. Таким образом, мы получим правильную обыкновенную дробь, которую можно записать в виде отношения двух целых чисел. Например, если результатом нашего вычисления была дробь 10/2, мы можем упростить ее, разделив числитель и знаменатель на их общий делитель 2. Таким образом, получается дробь 5/1.

Как перевести обыкновенную дробь 1 2 в десятичную

Для перевода обыкновенной дроби 1/2 в десятичную необходимо выполнить следующие действия. Сначала делим числитель 1 на знаменатель 2. В данном случае результат деления равен 0 с остатком 1. Так как 1 не делится на 2 нацело, записываем в ответе цифру 0 перед запятой. Затем ставим запятую и переносим остаток 1 в виде десятых долей. Теперь делим получившуюся десятичную дробь 10 на 2. Результат деления равен 5. Таким образом, в ответе после запятой получается цифра 5. Итоговый результат перевода дроби 1/2 в десятичную представляет собой число 0,5.

Как разделить десятичную дробь на 0 1 0 01 и так далее

Для начала нужно установить, какое количество цифр после запятой имеется в делителе. После этого необходимо переместить запятую в делимом числе на столько позиций вправо, сколько цифр после запятой в делителе. Второй способ заключается в умножении делимого и делителя на \(10\), \(100\), \(1000\) и так далее, чтобы получить новые числа без десятичной части. Затем мы можем произвести деление. Например, если мы хотим разделить десятичную дробь \(0,25\) на \(0,01\), необходимо переместить точку в десятичной дроби на два разряда вправо. Получившееся число будет равно \(25\), а делитель также умножим на \(100\), то есть будет равен \(1\). Таким образом, результатом деления будет число \(25\).