Калькулятор сравнения дробей

Калькулятор сравнения десятичных дробей — Как сравнивать десятичные дроби?

Введите десятичные значения, и наш инструмент покажет, какое из них больше или меньше.

1 st Номер:

2 nd Номер:

1	Что такое класс PriceEight?
2	Таблица класса priceeight:
3	Как рассчитать плотность priceeight (шаг за шагом):
4	Факторы, определяющие ценуВосьмая классификация:
5	Какова цель класса priceeight?
6	Упомянутая цена8 классов проверена официальными лицами?
7	Одинаковы ли классы цен для UPS и FedEx?

Получите виджет!

Добавьте этот калькулятор на свой сайт, чтобы пользователи могли выполнять простые расчеты.

Получить код

Обратная связь

Насколько легко было пользоваться нашим калькулятором? Сталкивались ли вы с какой-либо проблемой, сообщите нам!

ОБРАТНАЯ СВЯЗЬ

Онлайн-калькулятор сравнения десятичных знаков позволяет сравнить пару десятичных значений.

Что такое десятичные числа?

Определенные числа, содержащие как целые числа, так и десятичные части, называются десятичными числами.

Например;

В десятичном числе 23,568 23 — целая часть числа, а .568 — десятичная часть числа.

Помните, что часть десятичного числа, за которой следует десятичная точка, всегда меньше единицы. Кроме того, вы также можете превратить десятичные дроби в дроби, а затем сравнить их соответствующим образом.

Как сравнивать десятичные дроби?

Пример № 01:

Предположим, у нас есть пара десятичных чисел, как показано ниже:

23,548 и 41,848

Какое десятичное число больше? Позвольте нам сказать вам! Теперь мы сравним обе эти десятичные дроби, чтобы проанализировать, какая из них больше или меньше друг друга!

Поскольку первые числа обеих цифр 23 и 41 . Число 41 уже больше 23 . Вот почему мы можем сказать, что десятичное число с 41 больше, чем с 23 .

Пример № 02:

Какая десятичная дробь здесь больше, чем меньше?

56,187 и 56,157

Поскольку цифры перед запятой одинаковы, мы будем сравнивать цифры после запятой (по одному)

• Первые цифры после запятой для обоих чисел равны 1 , значит перейдём к следующим
• Следующие цифры 8 и 5 соответственно. Поскольку мы видим, что 8>5 , значит число 56,187 больше числа 56,157

Как работает калькулятор сравнения десятичных дробей?

Сравнить пару десятичных значений довольно легко и быстро с помощью нашего калькулятора сравнения десятичных знаков. Что вам нужно сделать, так это следовать приведенному ниже руководству, чтобы получить желаемые результаты:

Ввод:

Введите первый и второй десятичные знаки в соответствующие поля и нажмите кнопку расчета

Вывод:

Больше меньше десятичных знаков

Ссылки:

Из источника Википедии: Десятичное число, Происхождение, Десятичная запись, Десятичные дроби, Приближение действительных чисел, Бесконечное десятичное расширение, Десятичное вычисление

Из источника Академии Хана: Сравнение десятичных дробей (десятых и сотых)

Часто задаваемые вопросы:

Как преобразовать смешанное число (целое число и дробь) в десятичное? Чтобы преобразовать смешанное число в десятичное, сначала преобразуйте дробную часть в десятичную, разделив числитель на знаменатель. Затем прибавьте целое число к десятичному. Например, чтобы преобразовать 3 1/2 в десятичное число, сначала преобразуйте 1/2 в десятичное число (0,5), а затем прибавьте 3, чтобы получить 3,5.
Как преобразовать десятичную дробь в дробь? Чтобы преобразовать десятичную дробь в дробь, поместите десятичную дробь над степенью 10 (например, 100, 1000 и т. д.), чтобы десятичная дробь стала целым числом. Затем упростите дробь, если это необходимо. Например, чтобы преобразовать 0,75 в дробь, поместите его над 100, чтобы получить 75/100. Упростите дробь до 3/4.
Что такое повторяющаяся десятичная дробь? Повторяющееся десятичное число — это десятичное число, в котором одна или несколько цифр повторяются бесконечно. Например, 1/3 можно выразить повторяющейся десятичной дробью: 0,333… Цифры 3 повторяются бесконечно. Чтобы выразить повторяющуюся десятичную дробь в форме дроби, используйте черту над повторяющимися цифрами. Например, 0,333… можно выразить как 1/3.

Упрощение выражений, раскрытие скобок, разложение многочленов на множители

Калькулятор позволяет произвести некоторые алгебраические преобразования с выражениями. Результат выводится в нескольких вариантах упрощения/разложения/раскрытия скобок и пр.

Примеры:

$$x^4+x^2a^2+a^4$$ (разложить на множители)

$$\frac{6x^3-24x^2}{6x^3}$$ (разложить на множители)

$$(5x-2y^2)(5x+2y^2)$$ (раскрыть скобки)

$$(a-b)(a+b)(a^2+b^2)(a^4+b^4)(a^8+b^8)$$ (раскрыть скобки)

$$\frac{a^3-8}{a^2+2a+4}$$ (раскрыть скобки)

$$\frac{\left(\frac{2a}{2a+b}-\frac{4a^2}{4a^2+4ab+b^2}\right)}{\left(\frac{2a}{4a^2-b^2}+\frac{1}{b-2a}\right)}+\frac{8a^2}{2a+b}$$ (упростить выражение)

$$\frac{1-\sin ^4\left(x\right)-\cos ^4\left(x\right)}{2\sin ^4\left(x\right)}+1$$ (упростить выражение)

$$\left(\sqrt{a}-\frac{a}{\sqrt{a}+1}\right)\cdot \frac{a-1}{\sqrt{a}}$$ (упростить выражение)

Вычисление производных

Математический калькулятор может дифференцировать функции (нахождение производной) произвольного порядка в точке «x». Ввод производной в поле калькулятора осуществляется вызовом групповой кнопки f(x) и далее:f'(x) — производная первого порядка;f»(x) — производная второго порядка;f»'(x) — производная третьего порядка.fn(x) — производная любого n-о порядка.

Примеры дифференцирования:

$$f’\left(\sqrt{x^2-3x+17}\right)$$ (найти производную функции)

$$f’\left(\log \left(x+\sqrt{x^2+1}\right)\right)$$ (дифференцировать функцию)

$$f’\left(\arctan \left(x-\sqrt{x^2+1}\right)\right)$$ (вычислить производную)

$$f»\left(x^2\cos 2x\right)$$ (производная второго порядка)

$$f»\left(\log \left(\frac{1-x^2}{1+x^2}\right)\right)$$ (вычислить производную второго порядка)

$$f»’\left(\left(2x+1\right)^3\left(x-1\right)\right)$$ (дифференцировать функцию третьего порядка)

$$f^7\left(e^{3x}\sin 2x\right)$$ (вычислить производную седьмого порядка)

Перевод обыкновенных дробей в десятичные дроби

Обозначим последовательность, в которой мы будем разбираться с переводом обыкновенных дробей в десятичные дроби.

После этого мы пойдем дальше и покажем, как любую обыкновенную дробь (не только со знаменателями 10, 100, … ) записать в виде десятичной дроби. При таком обращении обыкновенных дробей получаются как конечные десятичные дроби, так и бесконечные периодические десятичные дроби.

Теперь обо всем по порядку.

Перевод обыкновенных дробей со знаменателями 10, 100, … в десятичные дроби

Некоторые правильные обыкновенные дроби перед переводом в десятичные дроби нуждаются в «предварительной подготовке». Это касается обыкновенных дробей, количество цифр в числителе которых меньше, чем количество нулей в знаменателе. Например, обыкновенную дробь 2/100 нужно предварительно подготовить к переводу в десятичную дробь, а дробь 9/10 в подготовке не нуждается.

«Предварительная подготовка» правильных обыкновенных дробей к переводу в десятичные дроби заключается в дописывании слева в числителе такого количества нулей, чтобы там общее количество цифр стало равно количеству нулей в знаменателе. Например, дробь

После подготовки правильной обыкновенной дроби можно приступать к ее обращению в десятичную дробь.

Рассмотрим применение этого правила при решении примеров.

Переведите правильную обыкновенную дробь 37/100 в десятичную.

Для закрепления навыков перевода правильных обыкновенных дробей с числителями 10, 100, … в десятичные дроби разберем решение еще одного примера.

Запишите правильную дробь 107/10 000 000 в виде десятичной дроби.

Разберем применение этого правила при решении примера.

Переведите неправильную обыкновенную дробь 56 888 038 009/100 000 в десятичную дробь.

Рассмотрим пример, при решении которого выполним все необходимые шаги для представления смешанного числа в виде десятичной дроби.

Переведите смешанное число

Запишем все решение кратко:

Перевод обыкновенных дробей в конечные и бесконечные периодические десятичные дроби

В остальных случаях приходится использовать другой способ перевода обыкновенной дроби в десятичную, к рассмотрению которого мы и переходим.

Для обращения обыкновенной дроби в десятичную дробь выполняется деление числителя дроби на знаменатель, числитель предварительно заменяется равной ему десятичной дробью с любым количеством нулей после десятичной запятой (об этом мы говорили в разделе равные и неравные десятичные дроби). При этом деление выполняется так же, как деление столбиком натуральных чисел, а в частном ставится десятичная запятая, когда заканчивается деление целой части делимого. Все это станет понятно из решений примеров, приведенных ниже примеров.

Переведите обыкновенную дробь 621/4 в десятичную дробь.

Так мы добрались до десятичной запятой в делимом, а остаток при этом отличен от нуля. В этом случае в частном ставим десятичную запятую, и продолжаем деление столбиком, не обращая внимания на запятые:

Для закрепления материала рассмотрим решение еще одного примера.

Переведите обыкновенную дробь 21/800 в десятичную дробь.

Запишите обыкновенную дробь 19/44 в виде десятичной дроби.

Для перевода обыкновенной дроби в десятичную выполним деление столбиком:

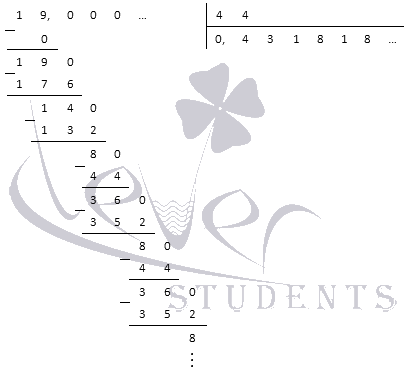
В заключение этого пункта разберемся, какие обыкновенные дроби можно перевести в конечные десятичные дроби, а какие – только в периодические.

Пусть перед нами находится несократимая обыкновенная дробь (если дробь сократимая, то предварительно выполняем сокращение дроби), и нам нужно выяснить, в какую десятичную дробь ее можно перевести – в конечную или периодическую.

Обыкновенные дроби не переводятся в бесконечные непериодические десятичные дроби

Информация предыдущего пункта порождает вопрос: «Может ли при делении числителя дроби на знаменатель получиться бесконечная непериодическая дробь»?

Ответ: нет. При переводе обыкновенной дроби может получиться либо конечная десятичная дробь, либо бесконечная периодическая десятичная дробь. Поясним, почему это так.

Других вариантов быть не может, следовательно, при обращении обыкновенной дроби в десятичную дробь не может получиться бесконечная непериодическая десятичная дробь.

Из приведенных в этом пункте рассуждений также следует, что длина периода десятичной дроби всегда меньше, чем значение знаменателя соответствующей обыкновенной дроби.

Сравнение фракций

Это означает, что минус минус в этом случае дает плюс, и сумма не изменяется от суммы. Те же правила, которые мы используем при подсчете фракций, один из которых отрицателен.

Чтобы решить смешанные фракции (фракции, в которых размещена вся часть), просто заполните всю фракцию во фракцию.

Чтобы сделать это, умножьте всю часть на знаменатель и добавьте его в счетчик.

Если вы хотите сохранить 3 или более акций в Интернете, они должны быть приняты. Во-первых, подсчитайте первые две фракции, затем с полученным ответом определите следующую долю и так далее. Выполните операции на линии 2 фракций, и в конце вы получите правильный ответ.

Системы счисления

Системы счисления делятся на два типа: позиционные и не позиционные. Мы пользуемся арабской системой, она является позиционной, а есть ещё римская − она как раз не позиционная. В позиционных системах положение цифры в числе однозначно определяет значение этого числа. Это легко понять, рассмотрев на примере какого-нибудь числа.

Пример 1. Возьмём число 5921 в десятичной системе счисления. Пронумеруем число справа налево начиная с нуля:

Число:	5	9	2	1
Позиция:	3	2	1

Число 5921 можно записать в следующем виде: = = . Число 10 является характеристикой, определяющей систему счисления. В качестве степеней взяты значения позиции данного числа.

Пример 2. Рассмотрим вещественное десятичное число 1234.567. Пронумеруем его начиная с нулевой позиции числа от десятичной точки влево и вправо:

Число:	1	2	3	4	5	6	7
Позиция:	3	2	1	-1	-2	-3

Число 1234.567 можно записать в следующем виде: = = .

Действия с десятичными дробями

Десятичные дроби – это обычные числа. Мы можем складывать их, вычитать из одной другую, умножать и делить.

Очень важно уметь правильно производить с ними математические действия, так как зачастую именно от арифметических ошибок зависит твоя оценка на экзамене. Несомненно, ты знаешь, как все это делать, но на всякий случай, дам тебе краткую инструкцию к применению. Несомненно, ты знаешь, как все это делать, но на всякий случай, дам тебе краткую инструкцию к применению

Несомненно, ты знаешь, как все это делать, но на всякий случай, дам тебе краткую инструкцию к применению.

Как складывать десятичные дроби

При сложении десятичные дроби записываются «столбиком», так чтобы одноимённые разряды находились друг под другом без смещения. Соответственно, запятые стоят четко друг под другом.

Разберемся на примере:

Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставится четко на том же месте, как и в складываемых числах.

Если исходные числа имеют разное количество знаков после запятой, то к дроби с меньшим количеством десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять в дробях количество знаков после запятой.

Если при сложении в сумме мы получаем больше \( 10\), то одна единица прибавляется к сумме при сложении цифр следующего разряда.

Решим наш пример, учтя все правила:

Разобрался? Посчитай в столбик самостоятельно:

• \( 0,0125+0,141\)
• \( 2,4225+0,34\)
• \( 122,4355+1,34\)
• \( 2,435+12,3\)

Сравним ответы:

• \( 0,0125+0,141=0,1535\)
• \( 2,4225+0,34=2,7625\)
• \( 122,4355+1,34=123,7755\)
• \( 2,435+12,3=14,735\)

Операции над дробями

С дробями можно совершать различные арифметические операции.

Сложение

Для сложения дробей с разными знаменателями сначала нужно найти знаменатель, который является общим. После этого нужно к общему знаменателю привести дроби. Хорошо, если это будет наименьший знаменатель.

Далее — выполнить сложение дробей, где под суммой числителей подписать общий знаменатель.

В конце, если возможно, сократить полученную дробь.

Например:

Вычитание

Здесь потребуется из числителя уменьшаемого отнять числитель вычитаемого, а сам знаменатель при этом оставить без изменений.

Так, чтобы сделать вычитание из дроби, следует сначала вычесть числители, а все одинаковые знаменатели оставлять прежними.

Например:

Умножение

Для этого умножаются числители и записывается результат, как числитель дроби.

Далее, умножаются знаменатели и записывается результат, как знаменатель дроби.

Например:

Деление

Здесь следует числитель первой дроби умножить на знаменатель второй дроби. После чего записать полученное произведение в числитель новой дроби.

Знаменатель первой дроби умножается на числитель второй дроби. Далее записывается произведение, как знаменатель новой дроби.

Например:

Сокращение

Это действие получается тогда, когда необходимо разделить числитель и знаменатель на одинаковое число, но которое не может быть равно 0.

В итоге получается равную дробь, имеющая меньший знаменатель и числитель.

Чтобы сократить дробь, необходимо в определенной последовательности проверять, на что делятся знаменатель и числитель. В случае, когда находится общий делитель, то сокращать именно на него.

Значительно упростит сокращение раскладывание знаменателя и числителя на множители.

Например:

Вопросы и ответы

А также советуем обратить внимание на некоторые часто задаваемые вопросы про дроби и ответы на них

Какие дроби называются простыми?

Простые дроби — это те, которые записываются в виде 2-ух целых чисел, определенных скошенной или горизонтальной прямой. Например: 1/4,1/2.

Когда в знаменателях стоят 10, 100, 1000 и т.д. и степень числа 10, то дроби имеют название — десятичные.

Правильные дроби те, у которых модуль знаменателя больше модуля числителя.

Неправильные дроби те, у которых модуль числителя меньше, чем модуль знаменателя.

Нельзя делить на 0.

Если делить на 1 — будет такое же число.

Если делить 0 на любое число, получится 0.

Когда она больше 0.

Когда перед положительной дробью ставится знак «–».

Что такое степени с дробями?

Степени с дробями приводятся к знаменателю так же, как и рациональные дроби. Нужно найти дополнительный множитель и умножить на него знаменатель и числитель дроби.

При этом дополнительный множитель подбирать так, чтобы он не обращался в 0 для исходящего выражения.

Как пользоваться калькулятором дробей?

Калькулятор, решающий дроби, позволяет переводить дроби и производить самые простые операции типа сложения, вычитания, умножения, деления.

Для этого нужно заполнить соответствующие поля для дробей и нажать кнопку «Вычислить».

Похожие калькуляторы

Возможно вам пригодятся ещё несколько калькуляторов по данной теме:

• Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
• Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
• Калькулятор логарифмов. Вычислите онлайн натуральные, десятичные логарифмы (или с другим основанием) с решением.
• Возведение дроби в степень. Возведите онлайн любую дробь (десятичную и обыкноенную) в любую степень.
• Калькулятор процентов от числа. Рассчитайте онлайн значение процента от любого числа с помощью данного калькулятора.
• Калькулятор процентов. Рассчитайте онлайн процент от числа, на сколько процентов одно число больше или меньше другого, или сколько процентов составляет одно число от другого числа, а также прибавьте или вычтете процент к числу.
• Добавить процент к числу. Прибавьте онлайн любой процент к любому числу с помощью специального калькулятора.
• Вычесть процент из числа. Вычтете онлайн любой процент от любого числа с помощью специального калькулятора.
• На сколько процентов больше. Рассчитайте онлайн, на сколько процентов одно число больше другого.
• На сколько процентов меньше. Рассчитайте онлайн, на сколько процентов одно число меньше другого.

Решение интегралов

Онлайн калькулятор предоставляет инструменты для интегрирования функций. Вычисления производятся как с неопределенными, так и с определенными интегралами. Ввод интегралов в поле калькулятора осуществляется вызовом групповой кнопки f(x) и далее:∫ f(x) — для неопределенного интеграла;b_a∫ f(x) — для определенного интеграла.

В определенном интеграле кроме самой функции необходимо задать нижний и верхний пределы.

Примеры вычислений интегралов:

$$\int \left(\frac{x^4}{x^3-6x^2+11x-6}\right)dx$$ (найти интеграл функции)

$$\int \left(\sqrt{x\sqrt{x\sqrt{x}}}\right)dx$$ (решить интеграл)

$$\int \left(\left(x^2+3x+5\right)\cos 2x\right)dx$$ (вычислить интеграл)

$$\int \left(\frac{x+\arccos ^2\left(3x\right)}{\sqrt{1-9x^2}}\right)dx$$ (решить интеграл)

$$\int _1^{e^3}\left(\frac{1}{x\sqrt{1+\log \left(x\right)}}\right)dx$$ (найти интеграл функции)

$$\int _{\frac{\pi }{6}}^{\frac{\pi }{3}}\left(\sin 6x\sin 7x\right)dx$$ (решить интеграл)

$$\int _{+\infty }^{-\infty }\left(\frac{1}{\left(x^2+1\right)\left(x^2+4\right)}\right)dx$$ (решить интеграл)

$$\int _1^2\left(x^2+\frac{1}{x}+\frac{1}{x^3}\right)dx$$ (вычислить интеграл)

Преобразование дроби в десятичную

Преобразование дроби в десятичную — это обычная математическая операция, которая включает в себя деление числителя (верхнего числа) на знаменатель (нижнее число) дроби. Например, дробь 1/2 можно преобразовать в десятичную, разделив 1 на 2, что равно 0,5.
Чтобы преобразовать дробь в десятичную вручную, выполните следующие действия:
Разделите числитель на знаменатель с помощью калькулятора или деления в большую сторону.
Если в результате деления не получится целое число, результатом будет повторяющаяся десятичная дробь. Чтобы выразить повторяющуюся десятичную дробь, используйте черту над повторяющимися цифрами. Например, 1/3 можно выразить как 0,333…, где 3 повторяются бесконечно.
Чтобы использовать калькулятор преобразования дробей в десятичные, просто введите числитель и знаменатель дроби и нажмите «Рассчитать». Калькулятор автоматически разделит числитель на знаменатель и отобразит результат в виде десятичной дроби.

Сравнение дробей с одинаковыми знаменателями

Сравнение дробей с одинаковыми знаменателями
по сути является сравнением количества одинаковых долей. К примеру, обыкновенная дробь 3/7
определяет 3
доли 1/7
, а дробь 8/7
соответствует 8
долям 1/7
, поэтому сравнение дробей с одинаковыми знаменателями 3/7
и 8/7
сводится к сравнению чисел 3
и 8
, то есть, к сравнению числителей.

Из этих соображений вытекает правило сравнения дробей с одинаковыми знаменателями
: из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше, и меньше та дробь, числитель которой меньше.

Озвученное правило объясняет, как сравнить дроби с одинаковыми знаменателями. Рассмотрим пример применения правила сравнения дробей с одинаковыми знаменателями.

Пример.

Какая дробь больше: 65/126
или 87/126
?

Решение.

Знаменатели сравниваемых обыкновенных дробей равны, а числитель 87
дроби 87/126
больше числителя 65
дроби 65/126
(при необходимости смотрите сравнение натуральных чисел). Поэтому, согласно правилу сравнения дробей с одинаковыми знаменателями, дробь 87/126
больше дроби 65/126
.

Ответ:

Зачем вам нужен онлайн-калькулятор?

Дробный калькулятор онлайн
предназначен для обработки гладкий
и смешанный
дробей (с целым числом).

Решение фракций часто необходимо для студентов и студентов, а также для инженеров и выпускников. Наш калькулятор позволяет создавать следующие действия с частицами: расщепление фракций, умножение фракций, добавление фракций и вычитание фракций
. Калькулятор также может работать с корнями и ставками, а также с отрицательными числами, что делает его несколько раз превышает
аналогичные веб-приложения.

Простой калькулятор фракционной дроби онлайн поможет вам решить дела с фракциями, поэтому вам не нужно беспокоиться о том, как противодействовать фракции.

Он становится здесь автоматически
, поскольку само приложение вычисляет общий знаменатель и, наконец, показывает конечный результат.

Общий принцип сравнения десятичных дробей

Для каждой конечной десятичной и бесконечной периодической десятичной дробей существуют соответствующие им некоторые обыкновенные дроби. Следовательно, сравнение конечных и бесконечных периодических дробей возможно производить как сравнение соответствующих им обыкновенных дробей. Собственно, это утверждение и является общим принципом сравнения десятичных периодических дробей.

На основе общего принципа формулируются правила сравнения десятичных дробей, придерживаясь которых возможно не осуществлять перевод сравниваемых десятичных дробей в обыкновенные.

То же самое можно сказать и про случаи, когда происходит сравнение десятичной периодической дроби с натуральными числами или смешанными числами, обыкновенными дробями – заданные числа необходимо заменить соответствующими им обыкновенными дробями.

Если же речь идет о сравнении бесконечных непериодических дробей, то его обычно сводят к сравнению конечных десятичных дробей. Для рассмотрения берется такое количество знаков сравниваемых бесконечных непериодических десятичных дробей, которое даст возможность получить результат сравнения.

Глава 2. Сложение и вычитание натуральных чисел

§ 7. Сложение натуральных чисел. Свойства сложения

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

192

193

194

195

196

Решаем устно (страница 51)

страница 51

§8. Вычитание натуральных чисел

197

198

199

200

201

202

203

204

205

206

207

208

209

210

211

212

213

214

215

216

217

218

219

220

221

222

223

224

225

226

227

228

229

230

231

232

233

234

235

236

237

238

239

240

Решаем устно (страницы 56-57)

страницы 56-57

§9. Числовые и буквенные выражения. Формулы

241

242

243

244

245

246

247

248

249

250

251

252

253

254

255

256

257

258

259

260

261

262

263

264

265

266

§10. Уравнение

267

268

269

270

271

272

273

274

275

276

277

278

279

280

§11. Угол. Обозначение углов

281

282

283

284

285

286

287

288

289

290

291

292

293

294

295

Решаем устно (страница 75)

страница 75

§12. Виды углов. Измерение углов

296

297

298

299

300

301

302

303

304

305

306

307

308

309

310

311

312

313

314

315

316

317

318

319

320

страница 81

§13. Многоугольники. Равные фигуры

321

322

323

324

325

326

327

328

329

330

331

332

333

334

335

336

337

страница 87

§14. Треугольник и его виды

338

339

340

341

342

343

344

345

346

347

348

349

350

351

352

353

354

355

356

357

358

Решаем устно (страница 92)

§15. Прямоугольник. Ось симметрии фигуры

359

360

361

362

363

364

365

366

367

368

369

370

371

372

373

374

375

376

377

378

379

380

381

382

383

Процесс счёта

Вверху представлены 4 кнопки быстрого доступа: к главной странице сайта, профилю пользователя. Также есть возможность включить/отключить звуковые уведомления или перейти к Подробному решению текущего примера.

Вы решаете заданый пример, вводите ответ по частям (целое, числитель, знаменатель) в соответствующие поля с помощью экранной клавиатуры, нажимаете на кнопку ПРОВЕРИТЬ. Если затрудняетесь дать ответ, воспользуйтесь подсказкой. После проверки ответа Вы увидите сообщение либо о правильно введенном ответе, либо об ошибке.

Количество правильных, неправильных ответов и число подсказок можно увидеть в соответствующих индикаторах.

Сравнение дробей с одинаковыми числителями

Следующий случай, в который мы можем попасть, это когда числители дробей одинаковые, но знаменатели разные. Для таких случаев предусмотрено следующее правило:

Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. И соответственно меньше та дробь, у которой знаменатель больше.

Например, сравним дроби и . У этих дробей одинаковые числители. У дроби знаменатель меньше, чем у дроби . Значит дробь больше, чем дробь . Так и отвечаем:

Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на три и четыре части. пиццы больше, чем пиццы:

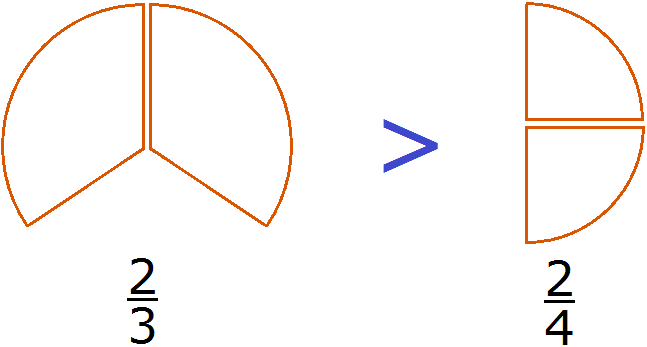
Каждый согласиться с тем, что первая пицца больше, чем вторая.

Таблица десятичных дробей

Существуют классические диаграммы, которые дают вам четкое представление об эквивалентности наиболее часто используемых дробей и их десятичных преобразованиях.

Калькуляторы о дробях и процентах

Естественно, как вы, вероятно, уже поняли, дроби, десятичные числа и проценты тесно связаны между собой. И часто это просто разные форматы для представления одной и той же информации более удобным способом для данного контекста.

Например, использование калькулятора процентов в дроби выполняет ту же работу, что и этот калькулятор десятичных дробей, с той разницей, что сначала вам нужно будет преобразовать десятичную дробь в проценты.

Естественно, вы можете столкнуться с обратной ситуацией. Может быть, вы хотите преобразовать

дробь до десятичной

, который является просто общим алгоритмом арифметики деления

Обратите внимание, что преобразование дроби в десятичную может привести к конечному десятичному числу или потенциально к повторяющемуся десятичному числу.

Например, дробь \(\displaystyle \frac{3}{5}\) соответствует простому числу 0,6 (простому конечному десятичному числу), а дробь \(\displaystyle \frac{1}{3}\) соответствует повторяющемуся десятичному числу 0,33333…..

Пример: Преобразование десятичной дроби в дробь

Вопрос

: Вычислите число 3,4563 как дробь.

Решение:

Вы ввели следующее десятичное число \(D = \displaystyle 3.4563\), и цель состоит в том, чтобы преобразовать его в дробь.

Шаг 1:

Нам нужно умножить \(D = 3.4563\) на степень 10, чтобы в результирующем выражении не было десятичных значений, справа от ‘.’ знак.

Шаг 2:

Это просто делается путем подсчета количества цифр справа от точки ‘.’. Для предоставленного номера у нас есть цифры \(k = 4\) справа от точки.

Следовательно, необходима степень числа 10 \(10^{k} = 10^{4} = 10000\). Следовательно, мы находим, что

Шаг 3:

Следовательно, мы находим, что

\

\

Итак, разделив обе части на \(10000\), мы получим

а поскольку найденная дробь уже упрощена, делается вывод, что простейшая дробь, эквивалентная \(3.4563\), равна \(3.4563\).

Следовательно, выражение десятичной дроби в простейшем виде — \(\displaystyle 3.4563 = \frac{ 34563}{ 10000}\), что завершает вычисление.