Решение логарифмических неравенств с разными основаниями егэ 15 задание

Метод замены переменной в неравенствах с логарифмом

Еще один очень популярный тип неравенств — это неравенства, которые решаются при помощи замены переменной. Как всегда, проще разобраться с этим на примерах:

Пример 5
$$\log_{3}^{2}(x)+2>3\log_{3}(x);$$
Сперва найдем ОДЗ, здесь оно крайне простое:
$$x>0.$$
Очень легкий пример, который решается при помощи замены

Действительно, обратите внимание, что логарифмы в неравенстве абсолютно одинаковые. Заменим их на какую-нибудь переменную \(t\):
$$Пусть \ t=\log_{3}(x)$$
Тогда неравенство примет вид:
$$t^2+2>3t;$$
$$t^2-3t+2>0;$$
Получили обыкновенное квадратное неравенство, только относительно переменной не \(x\), а \(t\)

Находим корни \(t\), раскладываем на множители и решаем методом интервалов:
$$(t-1)(t-2)>0;$$
$$t\in(-\infty;1)\cup(2;+\infty);$$
То же самое можно переписать в виде совокупности неравенств, смысл остается такой же:
$$\left[
\begin{gathered}
t \lt 1, \\
t \gt 2. \\
\end{gathered}
\right.$$
Не путайте совокупность и систему! Знак системы используется, когда нужно найти значения \(x\), удовлетворяющие ОДНОВРЕМЕННО всем неравенствам, входящим в систему.

А знак совокупности используется, когда нужно объединить решение каждого неравенства — то есть решением совокупности будут все корни, полученные в каждом неравенстве по отдельности.

В данном примере мы используем совокупность, так как нас устраивают и \(t \lt 1\), и \(t \gt 2\). И то, и то является решением нашего неравенства.

Понимание разницы между совокупностью и системой — принципиальный момент при решении логарифмических и показательных неравенств. С совокупностью мы познакомились в этом примере, а когда используется система, поговорим чуть позже.

Решение примеров

Задание. Давайте попробуем решить такое вот неравенство:

Решение области допустимых значений.

Теперь попробуем умножить его правую часть на:

Смотрим, что у нас получится:

Далее, следуя свойствам логарифмов, возьмем и внесем коэффициент –2, как степень подлогарифмического выражения и в итоге получим:

Теперь, давайте с вами перейдем к преобразованию подлогарифмических выражений. В связи с тем, что основание логарифма 0< 1/4 <1, то от сюда следует, что знак неравенства изменится на противоположный:

3x — 8 > 16;
3x > 24;
х > 8.

А из этого следует, что интервал, который мы получили, целиком и полностью принадлежит ОДЗ и является решением такого неравенства.

Вот какой ответ у нас получился:

Пример из ЕГЭ предыдущих лет №2 (на “сложную” замену переменной)

( displaystyle frac{lo{{g}_{{{7}^{x+3}}}}49}{lo{{g}_{{{7}^{x+3}}}}left( -49x right)}le frac{1}{lo{{g}_{7}}lo{{g}_{frac{1}{7}}}{{7}^{x}}})

Решение:

Вначале найдем ОДЗ:

( displaystyle left{ begin{array}{l}xne -1\xne -frac{1}{49}\xne -3\x<0end{array} right.)

Вы можете оспорить второе выражение системы. В самом деле, откуда оно берется?

А во всем виновато соотношение: ( displaystyle lo{{g}_{a}}b=frac{lo{{g}_{c}}b}{lo{{g}_{c}}a}), которое применимо к нашему случаю даст:

( displaystyle frac{lo{{g}_{{{7}^{x+3}}}}49}{lo{{g}_{{{7}^{x+3}}}}left( -49x right)}=lo{{g}_{left( -49x right)}}49=frac{1}{lo{{g}_{49}}left( -49x right)}=frac{1}{1+lo{{g}_{49}}left( -x right)}=frac{2}{2+lo{{g}_{7}}left( -x right)})

Второе выражение преобразуем вот так:

( displaystyle frac{1}{lo{{g}_{7}}lo{{g}_{frac{1}{7}}}{{7}^{x}}}=frac{1}{lo{{g}_{7}}left( -lo{{g}_{7}}{{7}^{x}} right)}=frac{1}{lo{{g}_{7}}left( -xlo{{g}_{7}}7 right)}=frac{1}{lo{{g}_{7}}left( -x right)}.)

Тогда наше неравенство преобразуется к вот такому виду:

( displaystyle frac{2}{2+lo{{g}_{7}}left( -x right)}le frac{1}{lo{{g}_{7}}left( -x right)}.)

Решение логарифмических неравенств

Теперь давай, наконец, запишем долгожданное правило.\( \displaystyle lo{{g}_{a}}~f\left( x \right)~>lo{{g}_{a}}~g\left( x \right)~=>~f\left( x \right)>g\left( x \right)\) при \( \displaystyle a>1\) \( \displaystyle lo{{g}_{a}}f\left( x \right)~>lo{{g}_{a}}~g\left( x \right)~=>~f\left( x \right)<g\left( x \right)\) при \( \displaystyle 0<a<1\)Если сказать все простыми словами, то:

Теперь ты понял, почему так сильно отличались решения очень похожих неравенств?

Вся собака зарыта в основаниях!

Теперь ты во всеоружии можешь решать самые разнообразные примеры, щелкая их как орешки (хотя не все орешки имеют мягкую скорлупу).

Вот тебе еще один пример:\( \displaystyle lo{{g}_{0.2}}\left( {{x}^{2}}+6x+8 \right)>lo{{g}_{0.2}}\left( 5x+10 \right)\).Ну что же, ты знаешь, что делать: вначале найдем ОДЗ (но здесь у нас будет аж два выражения в нем).

Во-первых \( \displaystyle {{x}^{2}}+6x+8>0\).

Как называется метод, который позволяет решать такие неравенства?

Да! Метод интервалов.

Я просил или нет, повторить его? Кажется, просил. И не зря. Тебя предупреждали, что он может пригодиться в самом неожиданном месте.

Ну ладно, я еще раз напомню, но в первый и последний раз делаю тебе маленькую поблажку.

Первое, что тебе нужно сделать, это найти корни уравнения \( \displaystyle {{x}^{2}}+6x+8=0\), как понимаешь, они равны \( \displaystyle x1=-4,\text{ }x2=-2.\)

Нанесем их на координатную прямую и разобьем ее на три интервала. Найдем знак нашего выражения на каждом из интервалов.

Для этого, как помнишь, я должен выбрать число из какого-нибудь промежутка и подставить его в исходное выражение.

Мне нравится подставлять ноль (не правда ли, удобно?), то есть я найду таким образом знак на крайне правом промежутке.

Выражение в нуле равно восьми, значит знак положительный. Ставлю плюсик. Далее чередую. Получу картинку:

Плюсики меня и интересуют, тогда ОДЗ первого выражения будет множество \( \displaystyle x\in \left( -\infty ;-4 \right)\mathop{\cup }^{}\left( -2;+\infty \right).\)

Второе ОДЗ проще: \( \displaystyle 5x+10>0\). Тут ты и сам справишься и запишешь, что \( \displaystyle x>-2\).

Тогда я пересекаю первое ОДЗ со вторым, получу:

Тогда мое окончательное ОДЗ – есть та область, над которой проходят две дужки – это промежуток \( \displaystyle \left( -2;+\infty \right).\)

Теперь приступим непосредственно к решению неравенства, оно заждалось и неприлично заставлять ждать его еще больше.\( \displaystyle lo{{g}_{0.2}}\left( {{x}^{2}}+6x+8 \right)>lo{{g}_{0.2}}\left( 5x+10 \right)\)Поскольку основание у нас \( \displaystyle 0.2<1,\), то ЗНАК НЕРАВЕНСТВА МЫ МЕНЯЕМ!!

Получим:\( \displaystyle {{x}^{2}}+6x+8<5x+10\)Упростим: \( \displaystyle {{x}^{2}}+{x} -2<0\)И опять применяем метод интервалов. Я пропущу эти выкладки, а ты проведи их и сравни с моим ответом:\( \displaystyle x\in \left( -2;1 \right).\)Окончательное решение неравенства – пересечение ОДЗ с только что полученным множеством. Получим:

Ответом будет голубой холмик, который ты видишь на картинке.

Преобразование логарифмических неравенств

Часто исходное неравенство отличается от приведенного выше. Это легко исправить по стандартным правилам работы с логарифмами — см. «Основные свойства логарифмов ». А именно:

1. Любое число представимо в виде логарифма с заданным основанием;
2. Сумму и разность логарифмов с одинаковыми основаниями можно заменить одним логарифмом.

Отдельно хочу напомнить про область допустимых значений. Поскольку в исходном неравенстве может быть несколько логарифмов, требуется найти ОДЗ каждого из них. Таким образом, общая схема решения логарифмических неравенств следующая:

1. Найти ОДЗ каждого логарифма, входящего в неравенство;
2. Свести неравенство к стандартному по формулам сложения и вычитания логарифмов;
3. Решить полученное неравенство по схеме, приведенной выше.

Найдем область определения (ОДЗ) первого логарифма:

Решаем методом интервалов. Находим нули числителя:

3x
− 2 = 0;x
= 2/3.

Затем — нули знаменателя:

x
− 1 = 0;x
= 1.

Отмечаем нули и знаки на координатной стреле:

Получаем x
∈ (−∞ 2/3)∪(1; +∞). У второго логарифма ОДЗ будет таким же. Не верите — можете проверить. Теперь преобразуем второй логарифм так, чтобы в основании стояла двойка:

Как видите, тройки в основании и перед логарифмом сократились. Получили два логарифма с одинаковым основанием. Складываем их:

log 2 (x
− 1) 2
log 2 (x
− 1) 2

Получили стандартное логарифмическое неравенство. Избавляемся от логарифмов по формуле. Поскольку в исходном неравенстве стоит знак «меньше», полученное рациональное выражение тоже должно быть меньше нуля. Имеем:

(f
(x
) − g
(x
)) · (k
(x
) − 1)
((x
− 1) 2 − 2 2)(2 − 1) x
2 − 2x
+ 1 − 4 x
2 − 2x
− 3
(x
− 3)(x
+ 1) x
∈ (−1; 3).

Получили два множества:

1. ОДЗ: x
   ∈ (−∞ 2/3)∪(1; +∞);
2. Кандидат на ответ: x
   ∈ (−1; 3).

Осталось пересечь эти множества — получим настоящий ответ:

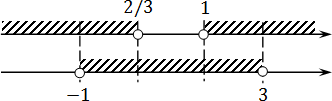
Нас интересует пересечение множеств, поэтому выбираем интервалы, закрашенные на обоих стрелах. Получаем x
∈ (−1; 2/3)∪(1; 3) — все точки выколоты.

Вам кажется, что до ЕГЭ еще есть время, и вы успеете подготовиться? Быть может, это и так. Но в любом случае, чем раньше школьник начинает подготовку, тем успешнее он сдает экзамены. Сегодня мы решили посвятить статью логарифмическим неравенствам. Это одно из заданий, а значит, возможность получить дополнительный балл.

Вы уже знаете, что такое логарифм(log)? Мы очень надеемся, что да. Но даже если у вас нет ответа на этот вопрос, это не проблема. Понять, что такое логарифм очень просто.

Почему именно 4? В такую степень нужно возвести число 3, чтобы получилось 81. Когда вы поняли принцип, можно приступать и к более сложным вычислениям.

Неравенства вы проходили еще несколько лет назад. И с тех пор они постоянно встречаются вам в математике. Если у вас проблемы с решением неравенств, ознакомьтесь с соответствующим разделом.
Теперь, когда мы познакомились с понятиями по отдельности, перейдем к их рассмотрению в общем.

Самое простое логарифмическое неравенство.

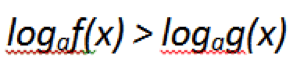
Простейшие логарифмические неравенства не ограничиваются этим примером, есть еще три, только с другими знаками. Зачем это нужно? Чтобы полнее понять, как решать неравенство с логарифмами. Теперь приведем более применимый пример, все еще достаточно простой, сложные логарифмические неравенства оставим на потом.

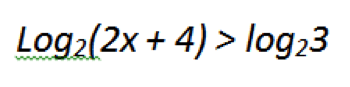
Как это решить? Все начинается с ОДЗ. О нем стоит знать больше, если хочется всегда легко решать любое неравенство.

Практика.

Решим неравенства:

1. $\log_{2}{(x+3)} \geq 3.$

Для начала найдём область определения:

$D(y): \ x+3>0.$

$\ x>-3$

$x \in (-3;+\infty)$

Основание логарифма равно $2>1$, поэтому знак не меняется. Пользуясь определением логарифма, получим:

$x+3 \geq 2^{3},$

$x+3 \geq 8,$

$x \geq 5,$

$x \in [5; + \infty).$

Соединяя полученное решение с областью определения, получим: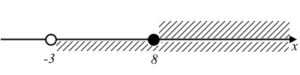Ответ: $x \in [5; +\infty)$.

2.  $\log_{\frac{1}{3}}{(x-2)} > -2.$

Для начала найдём область определения:

$D(y): \ x-2>0.$

$\ x>2$

$x \in (2;+\infty)$

Основание равно $\frac{1}{3}<1$, а, значит, знак неравенства меняется на противоположный. Получаем:

$x-2<\left(\frac{1}{3}\right)^{-2},$

$x-2<9,$

$x<11,$

$x \in (- \infty; 11).$

Соединяя полученное решение с областью определения, получим:

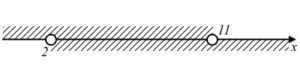Ответ: $x \in (2; 11).$

Разберём теперь более сложный пример из задания C1 экзамена.

3. $\log_{3}{(2x+1)} \geq \log_{\frac{1}{3}}{\left(\frac{1}{7-x}\right)}$.

Для начала найдём область определения:

$D(y): \ 2x+1>0, \ \frac{1}{7-x}>0, \ 7-x \neq 0,$

$2x+1>0, \ 7-x>0, \ 7-x \neq 0,$

таким образом, третье неравенство излишне (второе уже не допускает равенства!) , получим:

$x>-0,5, \ x<7,$

$x \in (-0,5;7).$

Преобразуем логарифм, стоящий в правой части, используя пятое и шестое свойство из статьи «Логарифм и его свойства«.

$\log_{\frac{1}{3}}{\left(\frac{1}{7-x}\right)}=\frac{1}{-1}\log_{3}{\left(\frac{1}{7-x}\right)}=-\log_{3}{\left(\frac{1}{7-x}\right)}=\log_{3}{\left(\frac{1}{7-x}\right)^{-1}}=$

$=\log_{3}{(7-x)}.$

Таким образом, получено следующее неравенство:

$\log_{3}{(2x+1)} \geq \log_{3}{(7-x)}$.

Основание равно $3>1$, а, значит, знак неравенства не меняется. Получаем:

$2x+1 \geq 7-x,$

$3x \geq 6,$

$x \geq 2,$

$x \in [2; +\infty).$

Соединяя полученное решение с областью определения, получаем ответ.

Ответ: $x \in [2; 7).$

Решение логарифмических неравенств

В школьном курсе алгебре и начала математического анализа в основном рассматриваются логарифмические неравенства вида $$ \log _a f\left( x \right) \vee \log _a g\left( x \right)$$, где $$ a > 0,{\rm{ }}a \ne 1 $$. При решении неравенств такого вида используется непосредственно монотонность логарифмической функции, учитывая область определения этой функции. Наиболее рациональное решение считается решение методом равносильных преобразований. Если в процессе решения смысл неравенства должен измениться, то символ $$ \vee $$ меняется на символ $$ \wedge$$. Например, $$\left( { — x} \right) \vee 0 \Leftrightarrow x \wedge 0$$.

Равносильные преобразования логарифмических неравенств:

1. $$ \left\{ \begin{array}{l} \log _a f\left( x \right) \wedge \log _a g\left( x \right); \\ 0 < a < 1 \\ \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} f\left( x \right) \wedge g\left( x \right); \\ f\left( x \right) > 0; \\ g\left( x \right) > 0. \\ \end{array} \right. $$.

2. $$ \left\{ \begin{array}{l} \log _a f\left( x \right) \vee \log _a g\left( x \right); \\ a > 1 \\ \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} f\left( x \right) \vee g\left( x \right); \\ f\left( x \right) > 0; \\ g\left( x \right) > 0. \\ \end{array} \right. $$.

Если вместо символа $$\vee$$ поставить конкретный знак сравнения, то равносильные системы логарифмическим неравенствам имеют вид:

1.1 $$\left\{ \begin{array}{l} \log _a f\left( x \right) \ge \log _a g\left( x \right); \\ 0 < a < 1. \\ \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} f\left( x \right) \ge g\left( x \right); \\ f\left( x \right) > 0. \\ \end{array} \right.$$

1.2 $$\left\{ \begin{array}{l} \log _a f\left( x \right) \le \log _a g\left( x \right); \\ 0 < a < 1. \\ \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} f\left( x \right) \ge g\left( x \right); \\ g\left( x \right) > 0. \\ \end{array} \right.$$

2.1 $$\left\{ \begin{array}{l} \log _a f\left( x \right) \ge \log _a g\left( x \right); \\ a > 1. \\ \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} f\left( x \right) \ge g\left( x \right); \\ g\left( x \right) > 0. \\ \end{array} \right.$$

2.2 $$\left\{ \begin{array}{l} \log _a f\left( x \right) \le \log _a g\left( x \right); \\ a > 1. \\ \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} f\left( x \right) \le g\left( x \right); \\ f\left( x \right) > 0. \\ \end{array} \right.$$

III. Неравенства вида logf(x)h(x)

Последняя группа стандартных
логарифмических неравенств, содержащих
неизвестную в основании логарифма, –
неравенства, левая и правая части которых
представляют собой логарифмы с разными
основаниями от одной и той же функции.
Равносильная система и в этом случае получается
с помощью преобразований, аналогичных
рассмотренным ранее.

Отметим, что эти преобразования применимы и в
случае неравенства противоположного знака, и в
случае нестрогих неравенств

Последнее особенно
важно, поскольку случай равенства h(x) единице
будет учтен в соответствующей системе, что
позволит избежать потери решения, которая часто
происходит при традиционном решении путем
перехода к основанию h(x)

Пример 5. Решите неравенство

Решение.

Ответ:

Не вызывает сомнений, что в ряде случаев
изложенный метод позволяет решать
логарифмические неравенства, содержащие
переменную в основаниях логарифмов, быстрее и
эффективнее других методов. Соответствующие
примеры легко найти во многих задачниках,
например, в или .

Литература

Неравенства с логарифмами по переменному основанию

Что, если в основании логарифма будет стоять не положительное число, а некоторое выражение, зависящее от \(x — \log_{g(x)}f(x)\)? Такие логарифмы называются логарифмами с переменным основанием.

Разберемся, как решать, на примере:

Пример 8
$$ \log_{\frac{x}{3}}(3x^2-2x+1) \ge 0;$$

Начнем решение с ОДЗ

Обратите внимание, что условия накладываются еще и на основание логарифма — оно должно быть больше нуля и не равно единице:
$$ \begin{cases}
3x^2-2x+1>0;, \\
\frac{х}{3}>0; ,\\
\frac{x}{3}\neq1.
\end{cases}$$. Заметим, что данный квадратный многочлен больше нуля при любых значениях \(x\)

Второе неравенство имеет решения при \(x \gt 0\). А третье дает нам \(x\neq 3\).
Объединяя все решения, получаем итоговое ОДЗ:
$$x\in(0;3)\cup(3;+\infty);$$

Заметим, что данный квадратный многочлен больше нуля при любых значениях \(x\). Второе неравенство имеет решения при \(x \gt 0\). А третье дает нам \(x\neq 3\).
Объединяя все решения, получаем итоговое ОДЗ:
$$x\in(0;3)\cup(3;+\infty);$$

Приступим к решению.
Мы знаем, чтобы решить исходное неравенство, нужно представить \(0\) справа в виде логарифма с таким же основанием. Но проблема в том, что основание логарифма слева не число, а выражение, зависящее от \(x\). Нас не должно это смущать, продолжаем решать точно так же, как если бы в основании было число, то есть, приводим к одинаковому основанию:
$$ \log_{\frac{x}{3}}(3x^2-2x+1) \ge \log_{\frac{x}{3}}\left(\frac{x}{3}\right)^0;$$
$$ \log_{\frac{x}{3}}(3x^2-2x+1) \ge \log_{\frac{x}{3}}(1);$$

Получилось, что сравниваются два логарифма с одинаковым основанием. Вот только это основание может быть совершенно любым

Это важно, если вспомнить, как решать классические логарифмические неравенства: знак неравенства должен меняться, если в основании логарифмов стоит число от нуля до единицы, и оставаться таким же, если основание больше единицы. У нас в основании стоит \(\frac{x}{3}\) — выражение, зависящее от \(x\)

Оно может принимать значения как больше единицы, так и меньше. Поэтому логично было бы рассмотреть два случая: когда основание больше \(1\), и когда от \(0\) до \(1\).

Основные положения и примеры решения простейших логарифмических неравенств.

С этим разделом могут ознакомиться и выпускники, которые планируют сдавать экзамен по математике на базовом уровне. На профильном экзамене встречаются более сложные неравенства, но их также тем или иным образом требуется сводить к простейшим.

К простейшим относятся логарифмические неравенства, которые содержат неизвестную переменную в составе аргумента логарифмической функции с фиксированным основанием, т.е. это неравенства вида
\(log_a{f(x)} > \log_a{g(x)}\), где \(a>0,\;a\ne1\) и неравенства, сводящиеся к этому виду. В более общих случаях неизвестная величина может встречаться и в основании логарифма.

Чтобы решать как логарифмические неравенства, так и логарифмические уравнения, нужно вспомнить определение и свойства логарифмической функции как таковой.
1) Логарифм – трансцендентная функция, т.е. аналитическая функция, которая не может быть задана с помощью алгебраического уравнения. Поэтому чтобы получить решение простейшего логарифмического неравенства, нужно сначала перейти к алгебраическим соотношениям, т.е. «убрать» логарифм. 2) Логарифм – однозначная и монотонная функция, что означает каждому значению аргумента из области определения соответствует единственное значение функции. Поэтому её можно сравнивать саму с собой и «вычёркивать» логарифм. Как и в каких случаях это делать, рассмотрим на примерых ниже. 3) Главное – логарифмическая функция имеет ограниченную область определения. Это означает, что при решении любых заданий с логарифмами, содержащими переменные, нужно не забывать про ОДЗ (область допустимых значений) этой переменной.

Логарифмом положительного числа \(x\) по основанию \(a\), где \(a>0,\; a\ne 1,\) называется показатель степени, в которую нужно возвести число \(a\), чтобы получить число \(x\). То есть равество \(\log_a{x} = y\) означает \(a^y = x.\)

Область значений функции E = R – всё множество действительных чисел. Т.е. сам логарифм, в отличие от его аргумента и основания, может принимать любые значения из промежутка \((-\infty; +\infty)\).

При a > 1 функция возрастающая,

при a < 1 функция убывающая.

Поэтому для решения простейших логарифмических неравенств достаточно преобразовать обе части неравенства к логарифму с одинаковым основанием и затем сравнить подлогарифмические выражения. Таким образом мы сравниваем функцию с самой собой при разных значениях её аргумента, т.е. как бы «вычёркиваем» log с обеих сторон неравенства. При этом, — если основание степени больше единицы, то знак неравенства без «log» будет таким же, как знак исходного неравенства, что характерно для возрастающих функций – большему значению аргумента соответствует большее значение функции; — если основание степени меньше единицы, то знак неравенства будет обратным по отношению к знаку исходного неравенства, что характерно для убывающих функций – большему значению аргумента соответствует меньшее значение функции.

Пример 1.

Решить неравенство \

Решение.

Воспользуемся определением логарифма, чтобы представить число −2 в виде значения логарифмической функции с основаением 0,2.

Ответ:

Пример 2

Решить неравенство: \

Решение.

Ответ: \(x \in (-\infty;-\sqrt2)\cup(\sqrt2;+\infty). \)

Замечание: Если вы не помните примерные значения иррациональных чисел или их нужно оценить точнее, пользуйтесь рекомендациями раздела сайта «Без калькулятора», в частности, страницей сравнение иррациональных выражений с единицей.

3.18. Метод рационализации

Метод рационализации — это процедура, позволяющая в определённых случаях упростить неравенство и свести его к рациональному неравенству (которое решается методом интервалов).

Позволяет перейти от выражения f к выражению g, сохранив все решения.

Метод рационализации для логарифмических неравенств

Здесь мы сравниваем значения относительно друг друга и допускаем случай, когда одно значение больше, а другое меньше и наоборот. Один из способов сравнения двух величин – это вычесть из одного другое. Если разность будет больше нуля, значит, первое число было больше. В первой скобке мы вычитаем из основания единицу. Это значит, что мы сравниваем основание с 1. Во второй скобке мы из одного под логарифмического выражения вычитаем другое, т.е. снова сравниваем их.

Пример. Решите неравенство

Решение.

ОДЗ:

Преобразуем неравенство

Воспользуемся методом рационализации:

Нам нужно найти такие х, при которых левое выражение меньше правого. В записанном неравенстве, если основание больше единицы, первая скобка будет положительна, и если первое подлогарифмическое выражение будет меньше второго, то их разность будет меньше 0, т.е. вторая скобка будет меньше нуля и это как раз те решения, что нужны нам по условию. Если же основание будет меньше единицы, первая скобка будет отрицательна, что изменит общий знак неравенства. Так же мы действовали, когда писали равносильный переход в виде двух случаев для логарифмического неравенства.

С учетом ОДЗ получаем решение неравенства:

Ответ:

Из рассмотренного метода рационализации вытекают следствия:

Пример. Решите неравенство:

Решение.

ОДЗ:

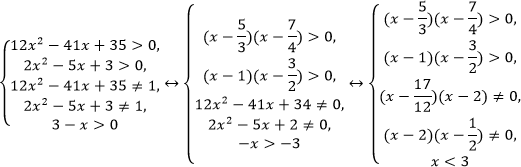
Применим метод рационализации:

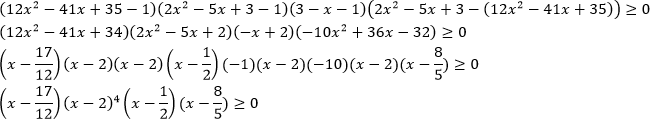
С учетом ОДЗ:

Ответ:

Метод рационализации для неравенств с модулем

При сравнении двух чисел по модулю нас не интересует знак числа, поэтому можем от знака избавиться при помощи чётной степени. избавит нас от знака. При дальнейшей работе с полученным неравенством выполнять возведение в квадрат не обязательно, лучше применить формулу разности квадратов.

Пример. Решите неравенство

Решение. Воспользуемся методом рационализации:

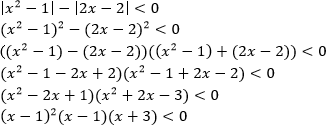
Решением неравенства является интервал (-3;1)

Ответ:

Пример. Решите неравенство

Решение. Воспользуемся равносильным переходом:

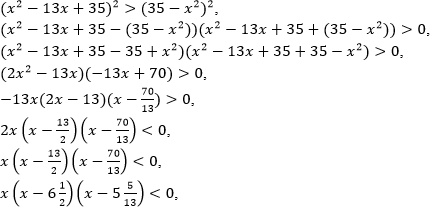
Решением неравенства является промежуток

Ответ:

Метод рационализации для иррациональных неравенств

Пример. Решите неравенство .

Решение.

ОДЗ (находим ОДЗ для меньшего из выражений, ОДЗ для большего выражения выполнится автоматически):

Воспользуемся методом рационализации:

С учетом ОДЗ получаем окончательное решение неравенства:

Ответ:

Метод рационализации для показательных неравенств

Для показательно-степенных неравенств действуют те же правила, что и для логарифма. При основании, большем 1, знак неравенства мы можем сохранить, при основании меньше единицы, знак неравенства должен измениться при переходе к степеням. Тогда мы можем записать это, как произведение двух скобок, в первой мы будем сравнивать основание с единицей, а во второй – значения показателей степеней.

Пример. Решите неравенство

ОДЗ:

Воспользуемся методом рационализации:

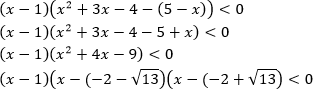
Видим, что решением является промежуток:

С учетом ОДЗ:

Ответ:

Сведем все рассмотренные равносильные преобразования в таблицу

Прочитано
Отметь, если полностью прочитал текст

Домашнее задание

Для лучшего усвоения темы и закрепления пройденного материала, решите следующие неравенства:

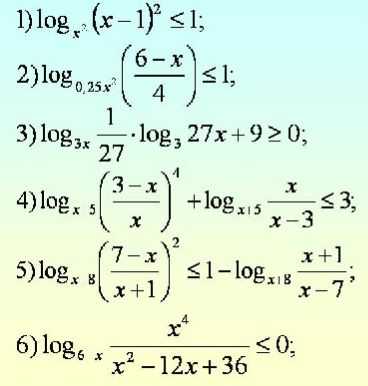
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию

Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Методы решения логарифмических неравенств не отличаются от , за исключением двух вещей.

Во-первых, при переходе от логарифмического неравенства к неравенству подлогарифмических функций следует следить за знаком получающегося неравенства
. Он подчиняется следующему правилу.

Во-вторых, решение любого неравенства – промежуток, а, значит, в конце решения неравенства подлогарифмических функций необходимо составить систему из двух неравенств: первым неравенством этой системы будет неравенство подлогарифмических функций, а вторым – промежуток области определения логарифмических функций, входящих в логарифмическое неравенство.