Различные способы сравнения дробей

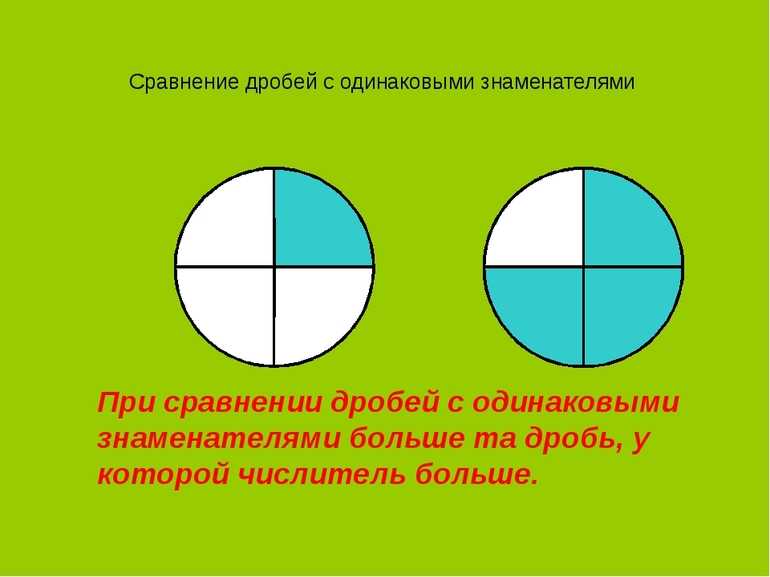
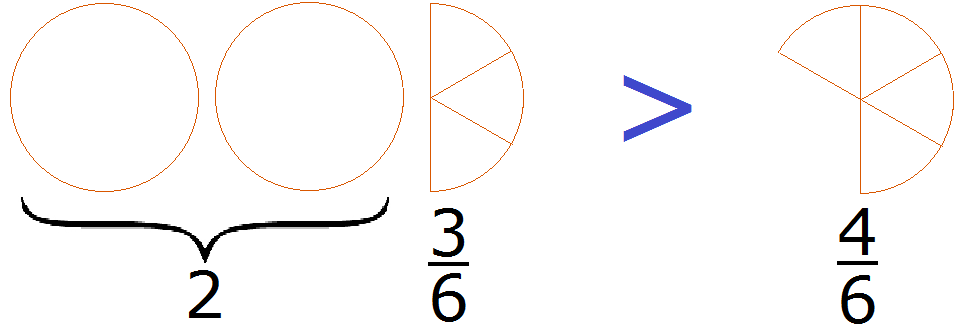Сравнение дробей с равными числителями.

Если у дроби одинаковые числители, то больше та дробь, у которой знаменатель меньше.

Понять это правило можно, если привести пример из жизни. У нас есть торт. К нам в гости могут прийти 5 или 11 гостей. Если придут 5 гостей, то мы разрежем торт на 5 равных кусков, а если придут 11 гостей, то разделим на 11 равных кусков. А теперь подумайте в каком случаем на одного гостя придется кусок торта большего размера? Конечно, когда придут 5 гостей, кусок торта будет больше.

Или еще пример. У нас есть 20 конфет. Мы можем поровну раздать конфеты 4 друзьям или поровну поделить конфеты между 10 друзьями. В каком случае у каждого друга будет конфет больше? Конечно, когда мы разделим только на 4 друзей, количество конфет у каждого друга будет больше. Проверим эту задачу математически.

\(\frac{20}{4} > \frac{20}{10}\)

Если мы до решаем эти дроби, то получим числа \(\frac{20}{4} = 5\) и \(\frac{20}{10} = 2\). Получаем, что 5 > 2

В этом и заключается правило сравнения дробей с одинаковыми числителями.

Рассмотрим еще пример.

Сравните дроби с одинаковым числителем \(\frac{1}{17}\) и \(\frac{1}{15}\) .

Так как числители одинаковые, больше та дробь, где знаменатель меньше.

\(\frac{1}{17}

Сравнение дробей с разными знаменателями

Сравнение таких дробей можно соотнести со сравнением дробей с одинаковыми показателями, но имеется различие. Теперь необходимо дроби приводить к общему знаменателю.

Если имеются дроби с разными знаменателями, для их сравнения необходимо:

• найти общий знаменатель;
• сравнить дроби.

Рассмотрим данные действия на примере.

Произвести сравнение дробей 5 12 и 9 16 .

В первую очередь необходимо привести дроби к общему знаменателю. Это делается таким образом: находится НОК, то есть наименьший общий делитель, 12 и 16 . Это число 48 . Необходимо надписать дополнительные множители к первой дроби 5 12 , это число находится из частного 48 : 12 = 4 , для второй дроби 9 16 – 48 : 16 = 3 . Запишем получившееся таким образом: 5 12 = 5 · 4 12 · 4 = 20 48 и 9 16 = 9 · 3 16 · 3 = 27 48 .

После сравнения дробей получаем, что 20 48 27 48 . Значит, 5 12 меньше 9 16 .

Ответ: 5 12 9 16 .

Имеется еще один способ сравнения дробей с разными знаменателями. Он выполняется без приведения к общему знаменателю. Рассмотрим на примере. Чтобы сравнить дроби a b и c d , приводим к общему знаменателю, тогда b · d , то есть произведение этих знаменателей. Тогда дополнительные множители для дробей будут являться знаменатели соседней дроби. Это запишется так a · d b · d и c · b d · b . Используя правило с одинаковыми знаменателями, имеем, что сравнение дробей свелось к сравнениям произведений a · d и c · b . Отсюда получаем правило сравнения дробей с разными знаменателями: если a · d > b · c , тогда a b > c d , но если a · d b · c , тогда a b c d . Рассмотрим сравнение с разными знаменателями.

Произвести сравнение дробей 5 18 и 23 86 .

Данный пример имеет a = 5 , b = 18 , c = 23 и d = 86 . Тогда необходимо вычислить a · d и b · c . Отсюда следует, что a · d = 5 · 86 = 430 и b · c = 18 · 23 = 414 . Но 430 > 414 , тогда заданная дробь 5 18 больше, чем 23 86 .

Ответ: 5 18 > 23 86 .

Сравнение дробей с одинаковыми числителями

Дроби с одинаковыми числителями сравниваются по значению их знаменателей. Знаменатель показывает, на сколько частей разделено целое число или количество объектов, а числитель указывает, сколько из этих частей мы рассматриваем.

Когда числители двух дробей одинаковые, чтобы сравнить эти дроби между собой, нужно сравнить знаменатели. Для этого нужно помнить, что знаменатель дроби показывает, на сколько равных частей разделено целое число или количество объектов.

Дробь	Знаменатель
1/3	3
1/5	5
1/8	8

Чем меньше знаменатель, тем больше каждая его часть репрезентативна (больше долей составляет один объект) и тем больше значение дроби. Следовательно, дробь с меньшим знаменателем будет больше.

• Дробь 1/3 имеет знаменатель 3.
• Дробь 1/5 имеет знаменатель 5.
• Дробь 1/8 имеет знаменатель 8.

Поэтому можно сделать вывод, что дробь 1/8 будет меньше, чем 1/5 и 1/3, так как значение каждой части в данной дроби составляет меньшую долю.

Сравнение дробей с разными числителями и разными знаменателями

Нередко случается так, что приходиться сравнивать дроби с разными числителями и разными знаменателями. Например, сравнить дроби  и .

Чтобы ответить на вопрос, какая из этих дробей больше или меньше, нужно привести их к одинаковому (общему) знаменателю. Затем можно будет легко определить какая дробь больше или меньше.

Приведём дроби  и  к одинаковому (общему) знаменателю. Найдём наименьшее общее кратное (НОК) знаменателей обеих дробей. НОК знаменателей дробей  и  это число 6.

Теперь находим дополнительные множители для каждой дроби. Разделим НОК на знаменатель первой дроби . НОК это число 6, а знаменатель первой дроби это число 2. Делим 6 на 2, получаем дополнительный множитель 3. Записываем его над первой дробью:

Теперь найдём второй дополнительный множитель. Разделим НОК на знаменатель второй дроби . НОК это число 6, а знаменатель второй дроби это число 3. Делим 6 на 3, получаем дополнительный множитель 2. Записываем его над второй дробью:

Умножим дроби на свои дополнительные множители:

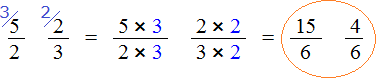
Мы пришли к тому что дроби, у которых были разные знаменатели, превратились в дроби, у которых одинаковые знаменатели. А как сравнивать такие дроби мы уже знаем. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше:

Правило правилом, а мы попробуем разобраться почему больше, чем . Для этого выделим целую часть в неправильной дроби . В дроби ничего выделять не нужно, поскольку эта дробь уже правильная.

После выделения целой части в дроби , получим следующее выражение:

Теперь можно легко понять, почему больше, чем .  Давайте нарисуем эти дроби в виде пицц:

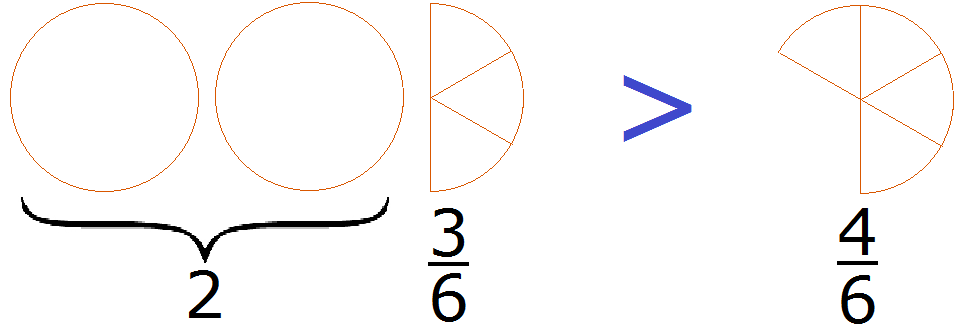
2 целые пиццы и пиццы, больше чем пиццы.

Равные дроби

Две дроби являются равными, если их числители и знаменатели соответственно равны (пропорционально равны).

Пример: дроби

Равны, т. к. числитель и знаменатель первой дроби в два раза меньше числителя и знаменателя второй дроби.

Равные дроби соответствует:

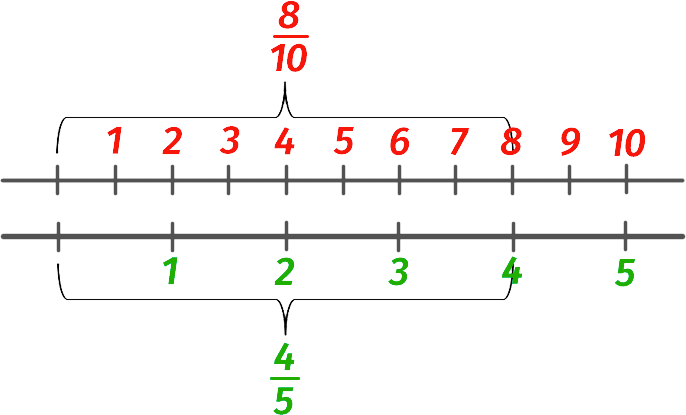
• одной и той же точке на числовой оси;
  одной и той же десятичной дроби, которая вычисляется путем деления числителя на знаменатель. В нашем случае 4/5 = 8/10 = 0,8.

Значит, .

Сравнение дробей с разными знаменателями и числителями

Теперь решим эту же задачу в общем виде, используя буквенную запись.

28.02.2019 17:04:59

2019-02-28 17:04:59

Любые данныеЛюбые данныеЛюбые данные Любые данные

Урок математики в 6-м классе по теме «Сравнение дробей»

Разделы: Математика

Задачи занятия Образовательные: научить учащихся сравнивать обыкновенные дроби различными способами Развивающие: развивать логическое мышление, познавательные и аналитические способности, учить самостоятельно, добывать новые знания, способствовать развитию правильной математической речи Воспитательные: формировать умение работать в коллективе, прислушиваться к мнению сверстников, взаимодействовать со взрослыми.

Этапы занятия	Временная реализация
Организационный момент: приветствие, объявление темы урока	3 минуты
Актуализация знаний	3 минуты
Создание различных проблемных ситуаций	15 минут
Промежуточное закрепление	10 минут
Самостоятельная работа	10 минут
Итог урока	4 минуты

1 этап (3 минуты)

Приветствие, объявление темы урока.

2 этап (3 минуты)

Как сравнить две обыкновенные дроби с одинаковыми знаменателями? Приведите пример.

Как сравнить две обыкновенные дроби с одинаковыми числителями? Приведите пример.

Как сравнить две обыкновенные дроби с разными знаменателями? Приведите пример.

С какими трудностями мы можем встретиться, сравнивая дроби с разными знаменателями?

Ученики — Иногда бывает трудно подобрать общий знаменатель, встречаются сложные вычисления.

Учитель — Оказывается ребята, наряду с уже хорошо известными нам способами сравнения обыкновенных дробей, существует несколько хитрых приемов, которые помогут нам сравнивать дроби проще и быстрее. Сейчас мы с вами и попробуем догадаться, что это за приемы.

3 этап (15 минут)

Учитель — Представьте частные в виде несократимых дробей:

Ученики — 1/2 2/3 3/4 4/5 5/6

Учитель — Что вы заметили?

Ученики — Числитель дроби на 1 меньше знаменателя.

Учитель — Как вы думаете, в каком порядке расположены дроби?

Ученики — В порядке увеличения.

Учитель — Как доказать?

Ученики — Можно привести к одному знаменателю.

Учитель — Отметьте эти точки на координатном луче, что вы заметили?

Ученики — Чем больше числитель и знаменатель, тем ближе расположено число к 1, т.е. 1/2 отличается от 1 на 1/2, 3/4 отличается от 1 на 1/4, 4/5 отличается от 1 на 1/5

1/2 > 1/3 >1/4 >1/5 > 1/6

Расстояния до 1 сокращаются, значит, сами числа увеличиваются!

Вывод: Обыкновенные дроби можно сравнивать, дополняя их до 1!

Учитель — Используя прием сравнения с 1, сравните:

Ученики —

Учитель — Как легче сравнить эти дроби? Приводя к одному знаменателю, или сравнивая с единицей?

Ученики — Конечно, сравнивая с единицей, так как иначе мы столкнемся со сложными вычислениями.

Учитель — Проанализируйте высказывание: если 3 · 7 14.05.2010

Источник

Сравнение дробей с разными знаменателями и числителями

Чтобы сравнить дроби, у которых разные числители и знаменатели, нужно привести их к общему знаменателю. После этого их сравнивают по правилу сравнения дробей, у которых одинаковые знаменатели.

Пример. Сравните дроби: И .

Решение: приводим данные дроби к общему знаменателю:

Теперь сравниваем их по правилу сравнения дробей, у которых одинаковые знаменатели. Так как , значит .

Приведём ещё один способ сравнения дробей с разными знаменателями и числителями. Рассмотрим сначала числовой пример.

Пример. Сравним дроби И .

Решение: приводим данные дроби к общему знаменателю:

Решая данный пример можно заметить, что, после приведения дробей к общему знаменателю, задача сравнения свелась фактически к сравнению произведений

Так как 2 · 7 = 14, а 4 · 3 = 12, то

Значит, .

Теперь решим эту же задачу в общем виде, используя буквенную запись.

Пример. Пусть даны дроби И , где A и C — нуль или натуральные числа, B и D — натуральные числа. Приведём дроби к общему знаменателю:

если A · D >C · B, то если A · DC · B, то если A · D = C · B, то

Таким образом мы получили следующее правило сравнения обыкновенных дробей:

Чтобы сравнить две обыкновенные дроби, можно числитель одной дроби умножить на знаменатель другой и полученные произведения сравнить.

Это правило называется Перекрёстным правилом сравнения дробей.

Единый знаменатель

Сравнить две обыкновенные дроби, имеющими разные знаменатели, является нелегкой задачей. Для этого требуется знать специальные методики приведения к единой величине.

Они подробно изучаются в 5 классе. Всего существует три ситуации, при которых применяется тот или иной тип алгоритма:

1. Знаменатель одной дроби «g» делится на другой «m» c образованием целого значения.
2. Величина «g» cодержит одинаковые множители с «m».
3. Другой случай.

Первая из них считается очень простой, т. к. для получения коэффициента нужно просто разделить одно значение на другое. Во втором случае необходимо находить наименьшее общее кратное (НОК), а в третьем — просто перемножить знаменатели, но с некоторыми особенностями. Следует разобрать каждую из трех ситуаций отдельно, поскольку требуется использовать совершенно разные методики.

Деление нацело

Приведение дробей с разными знаменателями, один из которых делится нацело на другой, выполняется по простой схеме. Она имеет такой вид:

1. Записать две величины: 2 (5/6) и 1 (9/12).
2. При необходимости преобразовать их в неправильные дроби: 17/6 и 21/12.
3. Вычислить коэффициенты при числителях: для первой — 12/6=2, для второй — 12/12.
4. Выполнить математические операции: 17*2/12=34/12 и 21/12.

Следует отметить, что в этом случае берется больший знаменатель. Он является единым для каждого из дробных выражений. Кроме того, всегда перед его поиском рекомендуется преобразовывать число в неправильную дробь. Это объясняется тем, что будет сложно выполнять математические операции.

Одинаковые сомножители

Одним из самых сложных случаев считается наличие в каждом знаменателе общих множителей. Для этого необходимо определить такое значение, какое будет делиться нацело на один и другой знаменатели. Оно называется в математике наименьшим общим кратным или сокращенно — НОК. Чтобы его найти, требуется воспользоваться таким алгоритмом на примере двух чисел 12 и 16:

1. Разложить каждое из них на множители: 12=2*2*3 и 16=2*2*2*2.
2. Найти повторяющиеся элементы: 2*2.
3. Умножить их на компоненты, которые являются разными для двух чисел: 2*2*(3*2*2)=48.

После нахождения НОК операция приведения дробных значений осуществляется по определенному алгоритму. Он имеет следующий вид:

1. Разделить НОК на каждый из знаменателей, записав над числителями определенные коэффициенты.
2. Выполнить математические преобразования.
3. Записать искомые результаты.

На практике нужно разобрать полную реализацию алгоритма. Она выглядит таким образом:

1. Записать дробные выражения: 3/12 и 7/16.
2. Найти НОК: НОК (12;16)=48.
3. Математические преобразования: 3*4/48=12/48 и 7*3/48=21/48.

Другой случай

Методика применяется при невозможности осуществить вышеописанные операции, т. е. оба числителя не содержат общих сомножителей и один из них не делится на другой. Математики назвали ее «крест-накрест». Следует отметить, что данный способ является очень простым. Его рекомендуется выполнять в том случае, когда ни один из методов не подходит. Он имеет следующий вид:

1. Записать дроби: 7/9 и 3/11.
2. Разделить знаменатели. Если получается дробное значение, то значит первый метод (деление нацело) не подходит: 11 на 9 не делится без остатка.
3. Попробовать разложить на общие множители: 11=11*1 и 9=3*3. Они отсутствуют.
4. Перейти после проверок к перекрестному образованию единого знаменателя: 9*11=99.
5. Записать коэффициенты над числителями и выполнить математические преобразования: 7*11/99=77/99 и 3*9/99=27/99.

Проверки во втором и третьем пунктах методики выполнять обязательно, поскольку данные меры помогут избежать множества ошибок при выполнении операций, позволяющих сравнить дроби обыкновенного типа.

Сравнение дробей с одинаковыми знаменателями

На двух скамейках стоят коробки. Длина каждой коробки составляет одну пятую часть от длины скамейки:

На первой скамейке $3$ коробки, а на второй — $2$, значит, коробки занимают $\frac{\textcolor{blue}{3}}{\textcolor{coral}{5}}$ и $\frac{\textcolor{blue}{2}}{\textcolor{coral}{5}}$ части скамейки соответственно. У нас получаются две дроби с одинаковыми $\textcolor{coral}{знаменателями}$, но разными $\textcolor{blue}{числителями}$.

Больше занята первая скамейка, поэтому мы можем сказать, что $\frac{3}{5}$ > $\frac{2}{5}.$

В неделе $5$ рабочих и $2$ выходных дня:

Выходные дни составляют $\frac{2}{7}$ от всех дней недели, а рабочие — $\frac{5}{7}$. Так как $2$ доли меньше, чем $5$ таких же долей, то $\frac{2}{7}$ < $\frac{5}{7}.$

читаем правильно

Выражение $\frac{2}{7}$ < $\frac{5}{7}$ правильно читается так: «Две седьмых меньше, чем пять седьмых».

{"questions":[{"content":"Если съесть $4$ прямоугольника шоколадки, оставшаяся часть будет больше или меньше съеденной?`image-1``choice-8`","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2021/08/shokoladka.svg","width":"450"},"choice-8":{"type":"choice","options":,"answer":}},"step":1,"hints":}]}

Сравнение дробей с разными числителями и знаменателями

Применяем третье правило:

Сравнение дробей с разными знаменателями нужно привести к сравнению дробей с одинаковыми знаменателями. Для этого необходимо привести дроби к общему знаменателю и использовать первое правило.

Например, необходимо сравнить дроби и . Для определения большей дроби приведем эти две дроби к общему знаменателю:

Теперь найдём второй дополнительный множитель: 6:3=2. Записываем его над второй дробью:

Продолжаем изучать дроби. Сегодня мы поговорим об их сравнении. Тема интересная и полезная. Она позволит новичку почувствовать себя учёным в белом халате.

Суть сравнения дробей заключается в том, чтобы узнать какая из двух дробей больше или меньше.

Чтобы ответить на вопрос какая из двух дробей больше или меньше, пользуются , такими как больше (>) или меньше (

Ученые-математики уже позаботились о готовых правилах, позволяющие сразу ответить на вопрос какая дробь больше, а какая меньше. Эти правила можно смело применять.

Мы рассмотрим все эти правила и попробуем разобраться, почему происходит именно так.

Содержание урока

Равные дроби

Представим, что мы съели $\frac{1}{4}$ пирога, но этого оказалось маловато, поэтому мы съели еще $\frac{1}{4}$ пирога. Получается, всего съедено $\frac{2}{4}$ пирога. И осталась еще половина. Выходит, что съедена тоже половина!

$\frac{2}{4} = \frac{1}{2}$

Отложим на координатном луче отрезок $\textcolor{purple}{OA},$ начало которого находится в точке $0,$ а конец расположен на расстоянии $\frac{2}{4}$ от начала:

Затем отложим отрезок $\textcolor{coral}{OB}$, который начинается в точке $0,$ но имеет длину $\frac{1}{2}$:

Мы видим, что точки $A$ и $B$ совпадают:

Две равные дроби обозначают одно и то же дробное число.

{"questions":[{"content":"На каком рисунке выделенная доля больше?`img_choice-1`","widgets":{"img_choice-1":{"type":"img_choice","options":[["https://obrazavr.ru/wp-content/uploads/2023/07/dolya1_2.svg","$\\frac{1}{2}$"],["https://obrazavr.ru/wp-content/uploads/2023/07/dolya1_3.svg","$\\frac{1}{3}$"],["https://obrazavr.ru/wp-content/uploads/2023/07/dolya1_4.svg","$\\frac{1}{4}$"]],"answer":}}}]}

Сравнение дробей с одинаковыми числителями

Если дроби имеют одинаковые числители и разные знаменатели, тогда можно выполнять сравнение по предыдущему пункту. Результат сравнения возможет при сравнении их знаменателей.

Имеется правило сравнения дробей с одинаковыми числителями из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот.

Рассмотрим на примере.

Произвести сравнение дробей 54 19 и 54 31 .

Решение

Имеем, что числители одинаковые, значит, что дробь, имеющая знаменатель 19 больше дроби, которая имеет знаменатель 31 . Это понятно, исходя из правила.

Ответ: 54 19 > 54 31 .

Иначе можно рассмотреть на примере. Имеется две тарелки, на которых 1 2 пирога, анна другой 1 16 . Если съесть 1 2 пирога, то насытишься быстрей, нежели только 1 16 . Отсюда вывод, что наибольший знаменатель при одинаковых числителях является наименьшим при сравнении дробей.

Решение примеров на сравнение дробей

1. Сравните две дроби \ и \.

Ответ: Мы видим, что знаменатели в данных дробях одинаковы. Здесь мы будем следовать правилу, согласно которому, когда знаменатели дроби одинаковы, дробь с меньшим числителем является меньшей дробью, а дробь с большим числителем считается большей дробью.

Итак, сравните числители 4>2

Следовательно,  \

2. Сравните две заданные дроби:  \ и \.

Ответ: Мы видим, что числители в данных дробях одинаковы. Здесь мы будем следовать правилу, что, когда дроби имеют одинаковый числитель, чем меньше знаменатель, тем больше дробь.

Итак, сравните знаменатели 13>20

Следовательно, \

3. Сравните данные дроби, используя метод перекрестного умножения: \ и \.

Ответ: Мы будем использовать метод перекрестного умножения, поэтому это означает, что необходимо умножить 3×10=30 и 5×8=40.

Здесь 30<40

Следовательно, \

4. Расположите дроби \ и \ в порядке возрастания.

Ответ: Сначала мы вычислим общий знаменатель, он равен 144.

Теперь запишем дроби как эквивалентные:

\

\
\

Так, 99 < 104 < 120, следовательно \

5. Что больше: \ или \?

Сравним с помощью десятичного метода.

Ответ: Мы можем использовать калькулятор 4÷8 и 6÷12. Теперь получаем, что \

Итак, обе доли равны 0,5 = 0,5

Следовательно, \

Общие сведения

Смешанная дробь — число, состоящее из целого значения и обыкновенного дробного выражения. Они образуются в результате операции деления. Последняя состоит из трех элементов, а именно: делимого, делителя и частного. Чтобы понять смысл смешанного числа, нужно разобрать дробные величины. К ним относятся следующие виды:

1. Обыкновенные.
2. Десятичные.

Обыкновенная дробь образуется посредством комбинации делимого и делителя, т. е. состоит всего из двух элементов. В этом случае частное имеет вид десятичного дробного тождества. Иными словами, десятичная дробь — величина, полученная при делении числителя на знаменатель.

Обыкновенные дробные выражения бывают двух видов: правильными и неправильными. У первых величина числителя меньше знаменателя, а у вторых — наоборот. Десятичные дроби делятся на 3 типа: с фиксированным количеством знаков после запятой, бесконечные периодические и непериодические.

У периодических дробных величин после запятой математические символы повторяются через определенный период, который указывается в круглых скобках. Например, число 4,(3) читается следующим образом: четыре целых и три в периоде.

Следует отметить, что бесконечные непериодические дробные выражения в их полном виде невозможно записать на листе бумаги, поскольку количество разрядов достигает бесконечности. Далее необходимо рассмотреть сокращение дробей, поскольку операция применяется для оптимизации конвертации неправильного дробного тождества в смешанное число.

Свойства дробей

Дроби, как и любые числовые выражения, обладают определенными свойствами. К ним относятся:

1. Если от числителя отнять одно значение, а затем его прибавить, дробь не изменится, т. е. (Q+T-T)/Z=Q/Z.
2. При умножении и делении на эквивалентное число величина дробного тождества не изменится, т. е. (Q*T)/(Z*Т)=Q/Z.

Первое утверждение проверить очень просто. Для этой цели нужно решить следующий пример, прибавив и отняв от числителя одно и то же значение: 7/8. Доказательство имеет такой вид:

1. Записать дробь: 7/8.
2. Взять произвольный коэффициент: 5.
3. Отнять, а затем прибавить его к числителю: (7−5+5)/8.
4. Числа «-5» и «5» являются противоположными. Их сумма равна 0, т. е. 5−5=0.
5. Если прибавить нуль к любому числу, получится искомая величина: 5+0=5.
6. Математические преобразования исходной дроби: (7−5+5)/8=/8=(7+0)/8.
7. Результат совпадает с искомым значением: 7/8=7/8.

Второе утверждение доказывается таким же простым способом на дроби ½. Для этого нужно решить пример (1*8)/(2*8) по следующему нестандартному алгоритму:

1. Записать дробное тождество: ½.
2. Коэффициент — общий множитель: 8. Последний необходимо представить в виде обыкновенной дроби: 8/8.
3. Величина «8/8» эквивалентна единице, которую можно умножить на любое число без потери значения выражения.
4. Расписать дробное значение: (½) * (8/8) = (½) * 1 = ½.
5. Сравнить результат и исходное значение: ½ = ½.
6. Утверждение доказано.

Некоторые ученики делают большую ошибку, отнимая (прибавляя) к числителю и знаменателю одну величину. Чтобы они не путали 2 утверждения сокращения, нужно привести пример и решить его:

1. Записать искомое значение: ½.
2. Коэффициент: 3.
3. Прибавить значение «3» к числителю и знаменателю: (1+3)/(2+3)=4/5.
4. Превратить искомое значение и величину в третьем пункте в десятичные дроби: 0,5 и 0,8.
5. Сравнить: 0,5 < 0,8.

Упрощение выражений

Преобразование любого арифметического выражения начинается с упрощения. Последнее применяется для уменьшения расчетов, при которых возникают ошибки. Упростить выражение — значит, сделать его более читабельным и предоставить возможность дальнейшего применения при расчетах. Иными словами, каждый результат должен «подгоняться» под мировой стандарт. Для сокращения дробей обыкновенного типа рекомендуется использовать такие правила:

1. Вынесения общего множителя за скобки и сокращение на него.
2. Формулы сокращенного умножения.
3. Приведение подобных слагаемых.

Первое правило позволяет найти единый множитель всего дробного выражения. После этого его можно будет разделить на одно и то же число. Формулы сокращенного умножения применяются также для реализации первого правила. Суть метода заключается в использовании специальных соотношений. Например, математическое выражение «1−25t 2 » выглядит таким образом: (1−5t)(1+5t).

После раскрытия скобок реализовывается третье правило — приведение подобных слагаемых. Они группируются по наличию однотипных элементов. Например, выражение 4t-4+t+t 2 −3+2t 2 имеет следующие одинаковые компоненты, которые группируются в скобках: (2t 2 +t 2 )+(4t+t)-(4+3). Если приводить подобные элементы, выражение упрощается, т. е. 3t 2 +5t-7.

Сравнение дробей с одинаковыми числителями

Следующий случай, в который мы можем попасть, это когда числители дробей одинаковые, но знаменатели разные. Для таких случаев предусмотрено следующее правило:

Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. И соответственно меньше та дробь, у которой знаменатель больше.

Например, сравним дроби и . У этих дробей одинаковые числители. У дроби знаменатель меньше, чем у дроби . Значит дробь больше, чем дробь . Так и отвечаем:

Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на три и четыре части. пиццы больше, чем пиццы:

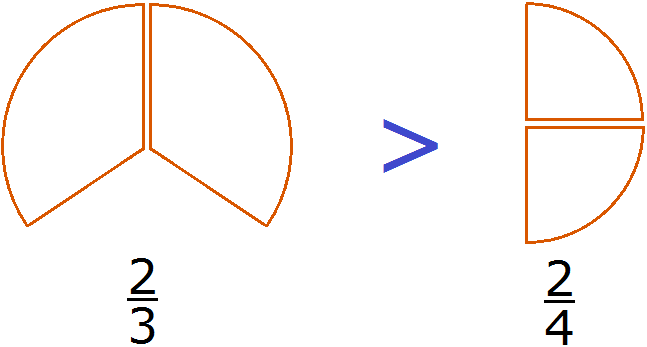
Каждый согласиться с тем, что первая пицца больше, чем вторая.