Нод и нок чисел — наибольший общий делитель и наименьшее общее кратное нескольких чисел

Возникновение «пустоты» или биография нуля

В математике \( \displaystyle  0\) – особенное число.

С первого взгляда, это ничто: прибавить \( \displaystyle  0\), отнять \( \displaystyle  0\) – ничего не изменится, но стоит только приписать его справа к «\( \displaystyle  1\)», и полученное число \( \displaystyle  10\) будет в \( \displaystyle  10\) раз больше изначального.

Умножением на ноль мы все превращаем в ничто, а разделить на «ничто», то есть \( \displaystyle  0\), мы не можем. Одним словом, волшебное число)

История нуля длинная и запутанная.

След нуля найден в сочинениях китайцев во 2 тыс. н.э. и ещё раньше у майя. Первое использование символа нуля, каковым он является в наши дни, было замечено у греческих астрономов.

Существует множество версий, почему было выбрано именно такое обозначение «ничего».

Некоторые историки склоняются к тому, что это омикрон, т.е. первая буква греческого слова ничто – ouden. Согласно другой версии, жизнь символу ноля дало слово «обол» (монета, почти не имеющая ценности).

Ноль (или нуль) как математический символ впервые появляется у индийцев (заметь, там же стали «развиваться» отрицательные числа).

Первые достоверные свидетельства о записи нуля относятся к 876 г., и в них «\( \displaystyle  0\)» – составляющая числа \( \displaystyle  270\).

В Европу ноль также пришел с запозданием — лишь в 1600г., и также как и отрицательные числа, сталкивался с сопротивлением (что поделаешь, такие они, европейцы).

«Нуль часто ненавидели, издавна боялись, а то и запрещали» — пишет американский математик Чарльз Сейф.

Так, турецкий султан Абдул-Хамид II в конце XIXв. приказал своим цензорам вычеркнуть из всех учебников химии формулу воды H2O, принимая букву «О» за нуль и не желая, чтобы его инициалы порочились соседством с презренным нулём».

Сложение. Группировка при сложении чисел

Что интересного ты можешь сказать про эту процедуру?

Конечно, ты сейчас ответишь «от перестановки слагаемых значение суммы не меняется». 

Казалось бы, примитивное, знакомое с первого класса правило, однако, при решении больших примеров оно моментально забывается!

Не забывай про него — используй группировку, чтобы облегчить себе процесс подсчета и снизить вероятность ошибок, ведь на ЕГЭ калькулятора у тебя не будет.

Смотри сам, какое выражение легче сложить?

• 4 + 5 + 3 + 6
• 4 + 6 + 5 + 3

Конечно же второе! Хотя результат один и тот же. Но! считая вторым способом у тебя меньше шансов ошибиться и ты все сделаешь быстрее!

Итак, ты в уме считаешь вот так:

Применение онлайн-калькулятора

Современные технологии позволяют не рассчитывать нужные данные на бумаге. Любой пользователь может найти в интернете НОД и НОК калькулятор, работающий в онлайн-режиме. Такой онлайн-сервис особенно удобен, если нужно найти делитель и кратное для 3 и более чисел.

Чтобы получить нужные расчеты, достаточно ввести в окошки калькулятора исходные данные и выбрать НОД или НОК. Поскольку между этими понятиями существует тесная связь, обычно они вычисляются вместе. Внизу находится кнопка «найти», которую нужно нажать. Через 2−3 секунды внизу появится ответ. Кроме того, некоторые сервисы выдают не только конечные результаты, но и пошаговый порядок расчетов. Здесь же можно найти онлайн-тесты на заданную тему.

Задачи на нахождение НОК

Мальчик хочет купить несколько пачек мороженного по 8 рублей, но у него только 5 рублевые монеты, а у продавца нет сдачи. Какое наименьшее число пачек мороженного он сможет купить?

1 способ. Нахождение НОК подбором:

Эта сумма должна делиться и на 8 рублей, и на 5 рублей без остатка.1) Выпишем числа кратные 8: 8, 16, 24, 32, 402) Выпишем числа кратные 5: 5, 10, 15, 20, 25, 30, 35, 40Выбираем наименьшее общее кратное. Нашли, эта сумма = 40 рублей. Теперь надо узнать сколько пачек можно купить на эту сумму: 40:8=5Ответ: мальчик может купить 5 пачек мороженного.

2 способ (общепринятый). Нахождение НОК в общем случае:

Эта сумма должна делиться и на 8 рублей, и на 5 рублей без остатка.

1) Выполним разложение 8 и 5 на простые множители.

8 | 2  5 | 54 | 2  1 |2 | 21НОК(8,5) = 8 * 5 = 40

2) Поскольку у нас нет одинаковых множителей, то для нахождения наименьшего общего кратного мы перемножаем эти числа между собой. Нашли НОК, т.е. эта сумма = 40 рублей. Теперь узнаем количество пачек мороженного

40 : 8 = 5 (п.)

Не забываем размерность и пишем ответ

Ответ: мальчик может купить 5 пачек мороженного.

Вдоль дороги от города (пункт А) до деревни (пункт В) были поставлены столбы через каждые 50 м. Их заменили другими, поставив на расстоянии 60 м друг от друга. Найдите расстояние от пункта А до ближайшего столба, который стоит на месте старого.

60 = 2·2·3·550 = 2·5·5

НОК(50;60) = 2·2·3·5·5 = 300 (м)

Ответ: 300 м от пункта А до ближайшего столба, который стоит на месте старого.

В одном городе начинаются три туристических теплоходных рейса. Первый длится 12 суток, второй — 18 суток, а третий — 21 сутки. Сегодня из города вышли теплоходы по всем трем маршрутам. Через сколько суток они снова вместе уйдут в плавание?

12 = 2·2·318 = 2·3·321 = 3·7

НОК(12;18;21) = 2·2·3·3·7 = 252 (сут.)

Ответ: через 252 суток они снова вместе уйдут в плавание.

В портовом городе начинаются три туристских теплоходных рейса, первый из которых длится 15 суток, второй – 20 и третий – 12 суток. Вернувшись в порт, теплоходы в этот же день снова отправляются в рейс. Сегодня из порта вышли теплоходы по всем трём маршрутам. Через сколько суток они впервые снова вместе уйдут в плавание? Какое количество рейсов сделает каждый теплоход?

Решение:

1) НОК (15,20 и 12) = 60 (суток) – время встречи. 2) 60 : 15 = 4 (рейса) – 1 теплоход. 3) 60 : 20 = 3 (рейса) – 2 теплоход. 4) 60 : 12 = 5 (рейсов) – 3 теплоход. Ответ: 60 суток, 4 рейса, 3 рейса, 5 рейсов.

Маша для Медведя купила в магазине яйца. По дороге в лес она сообразила, что число яиц делится на 2,3,5,10 и 15. Сколько яиц купила Маша?

Решение:

НОК (2;3;5;10;15) = 30 (яиц) Ответ: Маша купила 30 яиц.

Требуется изготовить ящик с квадратным дном для укладки коробок размером 16 ͯ 20 см. Какова должна быть наименьшая длина стороны квадратного дна, чтобы уместить коробки в ящик вплотную?

Решение:

1) НОК (16 и 20) = 80 (коробок). 2) S = a ∙ b – площадь 1 коробки.     S = 16 ∙ 20 = 320 ( см ² ) – площадь дна 1 коробки. 3) 320 ∙ 80 = 25600 ( см ² ) – площадь квадратного дна. 4) S = а² = а ∙ а     25600 = 160 ∙ 160 – размеры ящика. Ответ: 160 см — сторона квадратного дна.

Вдоль дороги от пункта К стоят столбы электролинии через каждые 45 м. Эти столбы решили заменить другими, поставив их на расстоянии 60 м друг от друга. Сколько столбов было и сколько будут стоять?

Решение:

1) НОК (45 и 60) = 180. 2) 180 : 45 = 4 – было столбов. 3) 180: 60 = 3 – стало столбов. Ответ: 4 столба, 3 столба.

Сколько солдат маршируют на плацу, если они будут маршировать строем по 12 человек в шеренге и перестраиваться в колонну по 18 человек в шеренге?

Решение:

1) НОК (12 и 18) = 36 (человек) – маршируют. Ответ: 36 человек.

Бегун Коля знает, что через каждые 400 м от старта стоит наблюдатель, а через каждые 700 м от старта можно попить воды. На каком минимальном расстоянии от старта можно попить воды и задать вопрос наблюдателю?

НОК(400;700) = 2800 (м)Ответ: 2800 м.

Длина шага Бори 50 см, а его отца – 70 см. Боря утверждает, что первый раз, сделав целое количество шагов, они с папой окажутся на одинаковом расстоянии от начала пути через 3 метра, а папа не соглашается. Кто прав в этом споре?

НОК(50;70)= 350 см, а не 3 метраОтвет: прав папа.

Заведующая хозяйством Раиса Максимовна дала поручение учителю труда Ильдару Олеговичу закупить доски, которые можно распилить на равные части и по 30 см, и по 40 см. Какой длины и сколько потребуется досок, если нужно 16 кусочков по 30 см и 12 кусочков по 40 см.

1) НОК(30; 40) = 120 (см)2) 16:(120:30) = 4 (д.)3) 12:(120:40) = 4 (д.)Ответ: всего 8 досок по 120 см.

Родители Артема – люди очень интересных профессий. Мама – стюардесса, а папа – машинист скорого поезда. Мама бывает дома один раз в четыре дня, а папа – один раз в семь дней. Так получилось, что оба они 1 января 2015 года уходят в рейс. Когда Артем увидит своих родителей дома вместе?

НОК(4;7) = 28Ответ: семья будет дома вместе 28 января.

Примеры нахождения наименьшего общего кратного

Рассмотрим приведенный алгоритм на конкретных примерах:

Пример 1: найти НОК 4 и 6

1. Раскладываем 6 и 4 на простые множители:

2. Возьмем первую группу множителей: 2 · 3.

3. Смотрим вторую группу (2 · 2) и видим, что из двух двоек, одна присутствует в первом разложении. Таким образом, берем только одну двойку. Добавляем к первому разложению и получаем: 2 · 3 · 2

4. Вычисляем произведение: 2 · 3 · 2 = 12.

Ответ: НОК (6; 4) = 12

Пример 2: найти НОК 32 и 20

1. Раскладываем 32 и 20 на простые множители:

2. Возьмем первую группу множителей: 2 · 2 · 2 · 2 · 2.

3. Смотрим вторую группу (2 · 2 · 5) и видим, что из двух двоек и пятерки, обе двойки присутствуют в первом разложении. Таким образом, берем только пятерку. Добавляем к первому разложению и получаем: 2 · 3 · 2

4. Вычисляем произведение: 2 · 2 · 2 · 2 · 2 · 5 = 160.

Примеры из реальной жизни

Общий знаменатель дробей

Наименьшее общее кратное используется для нахождения общего знаменателя нескольких дробей. Предположим, что в арифметической задаче необходимо сложить 5 дробей:

1/8 + 1/9 + 1/12 + 1/15 + 1/18.

Чтобы сложить дроби, выражение необходимо привести к общему знаменателю, что сводится к задаче нахождения НОК. Для этого выберите в калькуляторе 5 чисел и введите значения знаменателя в соответствующие ячейки. Программа вычислит НОК (8, 9, 12, 15, 18) = 360. Теперь вам нужно вычислить дополнительные множители для каждой дроби, которые определяются как отношение НОК к знаменателю. Таким образом, дополнительные факторы появятся как:

• 360/8 = 45
• 360/9 = 40
• 360/12 = 30
• 360/15 = 24
• 360/18 = 20.

Далее умножаем все дроби на соответствующий дополнительный множитель и получаем:

45/360 + 40/360 + 30/360 + 24/360 + 20/360.

Мы легко можем сложить эти дроби и получить результат в виде 159/360. Уменьшаем дробь на 3 и видим окончательный ответ — 53/120.

Примеры расчета НОК

Рассмотрим пример нахождения НОК для двух чисел: 12 и 18.

• Для начала найдем все простые множители для каждого числа: 12 = 2 * 2 * 3, 18 = 2 * 3 * 3;
• Запишем полученные множители в ряды: 12 = 2 * 2 * 3 * 1, 18 = 2 * 3 * 3 * 1;
• Выберем из каждого ряда наибольшее число повторений каждого множителя: 2 * 2 * 3 * 3 * 1 = 36;

Таким образом, НОК для чисел 12 и 18 равен 36.

Рассмотрим следующий пример для трех чисел: 4, 6 и 9.

• Найдем все простые множители для каждого числа: 4 = 2 * 2, 6 = 2 * 3, 9 = 3 * 3;
• Запишем полученные множители в ряды: 4 = 2 * 2 * 1, 6 = 2 * 3 * 1, 9 = 3 * 3 * 1;
• Выберем из каждого ряда наибольшее число повторений каждого множителя: 2 * 2 * 3 * 3 * 1 = 36;

НОК для чисел 4, 6 и 9 равен 36.

Таким образом, для нахождения НОК для нескольких чисел нужно найти все простые множители каждого числа, записать их в ряды и выбрать из каждого ряда наибольшее число повторений каждого множителя.

Алгоритм Евклида для нахождения НОД

Свой алгоритм Евклид (древнегреческий математик, живший примерно в 300 г. до
н.э.) придумал для решения задачи о соизмеримости двух отрезков. Общей мерой
(единицей измерения) отрезков с длинами $L_1$ и $L_2$ является отрезок
с наибольшей возможной длиной $L$, который можно уложить без остатка как в
первом отрезке, так и во втором. Например, для отрезков 10 и 15 такой общей мерой будет отрезок с длиной 5 (им
можно
пользоваться как единицей измерения для обоих отрезков). При этом 5 будет наибольшим общим
делителем
10 и 15.

В общем случае, алгоритм Евклида — это метод нахождения
наибольшего общего делителя (НОД) нескольких чисел.

Целое число $a$ делится на целое число $b$ ($b \ne 0$), если
существует целое число $k$, такое что $a=kb$. В таком случае $b$ называют делителем
числа $a$; число $a$ называют кратным числа $b$.

Если $a$ и $b$ делятся на $c$,
то их сумма $a+b$ и их разность $a-b$ делятся на $c$.

Если $a$ делится на $c$, а $b$ делится на $d$, то их
произведение $a*b$ делится на $c*d$.

$a$ и $b$ – положительные целые числа, $c$ — является общим делителем
чисел $a$ и $b$, если $a$ делится на $c$ и $b$ делится на $c$.

Среди общих делителей чисел $a$ и $b$ (не равных одновременно нулю) есть наибольший общий
делитель
(по-английски Greatest common divisor — GCD), обозначаемый НОД($a,b$) или $GCD(a,b)$.

Если $a$ делится на $b$, то $GCD(a,b) = b$. Например: $GCD(50,10)=10$.

$GCD(a,a)=a$. Например: $GCD(32,32)=32$.

Если $a \gt b$, то $GCD(a,b)=GCD(a-b,b)$.

Если $GCD(a,b)=1$, то числа $a$ и $b$ — взаимно простые.

Алгоритм Евклида с вычитаниями

Последовательно вычитая из большего числа меньшее до тех пор, пока они не станут равными, придем к НОД этих
чисел.

Пример: Найти НОД двух чисел 264 и 192.

Решение:
НОД(264, 192) = НОД(72, 192) = НОД(72, 120) = НОД(72, 48) =
НОД(24, 48) = НОД(24, 24) = 24

Задача. Найти НОД двух натуральных чисел $a$ и $b$.

Используем для решения задачи алгоритм Евклида с вычитаниями.

Реализация на Pascal:

function GCD( a,b:integer ):integer; { определение НОД двух чисел }
begin
  while a  b do
    if a > b then a:=a-b else b:=b-a;
  GCD := b;
end;

begin { Пример использования }
  writeln(GCD(10,15)); { Выведет 5 }
end.

Реализация на С/C++:

#include <stdio.h>

int GCD( int a, int b ){ // определение НОД двух чисел
  while(a != b)
    if (a > b) a-=b; else b-=a;
  return b;
}

int main(){ // Пример использования
  printf("%d",GCD(10,15)); // Выведет 5
  return 0;
}

Алгоритм Евклида с делением

Если применить алгоритм Евклида с вычитаниями к паре чисел $(1,10^{20})$, то будет выполнено около $10^{20}$
вычитаний, это слишком долго!

Можно за один раз вычитать из $a$ $b$ столько раз, сколько можно. Алгоритм Евклида с делением основан на том, что
если $a=bq+r$, где $r$ — остаток от деления $a$ на $b$ ($0 \le r

Последовательно
применяя это утверждение можно понять, что НОД двух чисел – это последний не
равный нулю остаток от деления большего числа на меньшее.

Пример: найти НОД двух чисел 6069 и 663.

Решение:

6069 = 663*9+102 НОД(6069, 663) = НОД
(663, 102)
663 = 102*6+51 НОД(663, 102) = НОД
(102, 51)
102 = 51*2+0 НОД(102, 51) = 51
(согласно утверждению 3)

Следовательно, 51 = НОД(102, 51) = НОД(663, 102) = НОД(6069, 663)

Демонстрационная Flash-программа показывает вычисление НОД любых 2 чисел:

Для содержимого этой страницы требуется более новая версия Adobe Flash Player.

Рассмотрим алгоритм и процедуру-функцию к решению задачи 1.1, используя для нахождения НОД двух
чисел алгоритм Евклида с делением.

Алгоритм:

Функция Вычисление_НОД(целое a, целое b)
  Пока (b <> 0)
    r := a по модулю b  (остаток от деления a на b), r - временная переменная (буфер)
    a := b
    b := r
  конец цикла
  Вывод результата - a
Конец функции

Реализация на Pascal:

function GCD( a,b:int64 ):int64; { Функция для вычисления НОД при помощи деления }begin  if b = 0 then { Если b = 0 }    GCD := a {  следовательно a=НОД }  else { Пока b <> 0 }    GCD := GCD(b,a mod b); { Вычисляем остаток от деления a на b, а заменяем на b, b заменяем на r }
end;

begin
  writeln(GCD(264, 192)); { Выведет: 24 }
end.

def GCD(a,b): # Функция для вычисления НОД при помощи деления
  return a if b == 0 else GCD(b,a%b) # Вычисляем остаток от деления a на b, а заменяем на b, b заменяем на r=a mod b
  # НОД = a если b = 0 иначе НОД=НОД(b,r), r - остаток от деления a на b

print GCD(264, 192) # Выведет: 24 

Вычислить НОД трех натуральных чисел $a$, $b$ и $c$ можно так:

$GCD(a,b,c)=GCD(GCD(a,b),c)$

В общем случае, справедлива следующая рекуррентная формула:

$GCD(a_1,a_2,…,a_n) = GCD(GCD(a_1,a_2,…,a_{n-1}), a_n)$.

Ниже приведена функция нахождения НОД для массива натуральных чисел $a(1..n)$ с использованием цикла.

function GCD( ... )...
    ....

function GCDM( a : array of int64 ):int64;
var d : int64; i : integer;
begin
  d := a;
  for i:= 1 to length(a)-1 do
    d := GCD(d, a);
  GCDM := d;
end;

begin { Пример вызова }
  writeln(GCDM());
end.  

Минутка истории

1. Древнегреческий математик Эвклид, создавший алгоритм нахождения НОД, совершил множество математических открытий, аналогов которым ученые не нашли. Самым интересным, является то, что биографических сведений о самом Эвклиде не существует.

2. Среди бесконечного множества простых чисел, заканчивающихся на два и пять, существует только два: 2 и 5.

3. Результат суммирования  цифр числа 18, в два раза меньше этого числа. Существует только одно число такого плана.

4. Однажды, математик Абрахам де Муавр, живший в Англии, находясь в преклонном возрасте, выяснил, что временной период, занимающий сон, увеличивается ежедневно на четвертую часть часа. Проведя вычисления, он определил день, когда длительность сна достигнет суток. По его расчетам это должно произойти двадцать седьмого ноября 1754 года. Именно эта дата стала датой смерти английского ученого.

Наибольший общий делитель

Встречаются ситуации, когда хочется понимать, на какое максимальное количество делится одновременно несколько числовых значений.

Например:

В городском парке проводился ежегодный марафон. Для участия в марафоне пришло 36 мальчиков, 24 девочки. По условиям соревнования, всех участников необходимо поделить на команды, в которые войдут  и мальчики, и девочки. Сколько одинаковых команд можно сформировать из данного количества детей?

Чтобы ответь на вопрос задачи, вычислим максимальное числовое значение, являющееся делителем для количества всех ребят одновременно.

Выполним необходимые вычисления – определим существующие множители. Вычисления запишем в столбик.

Начнем с 36.

36 | 2

18

Полученное частное – 18, оно четное. Делитель остается прежним:

36 | 2

18 | 2

9

9 – нечетное, поэтому берем следующий делитель – 3:

36 | 2

18 | 2

9  | 3

3

Частное – простое числовое значение, делится само на себя:

36 | 2

18 | 2

9  | 3

3  | 3

1

Частное – единица, разложение окончено.

Выпишем составляющие:

36 = 2×2×3×3

Переходим к 24.

24 заканчивается четной цифрой, значит, кратно двум:

242

12

Делитель оставляем прежним, частное 12 – четное:

242

122

6

Результат деления 6, снова делим на 2:

24 | 2

12 | 2

6  | 2

3

Получили простое числовое значение, которое делится само на себя:

24 | 2

12 | 2

6  | 2

3  | 3

1

Разложение окончено. Запишем полученные компоненты:

24 = 2 × 2 × 2 × 3.

В финале выполненных вычислений мы получили:

36 = 2 × 2 × 2 × 3× 3;

24 = 2 × 2 × 2 × 3.

Давайте выберем одинаковые составляющие. Видно, что в каждом выражении такими составляющими будут: 2 ×2 × 3.

Перемножим выделенные компоненты:

2 ×2 × 3 = 12.

12 – самое большое числовое значение, на которое можно разделить оба делимых.

Мы выяснили, что всех участников можно распределить на 12 одинаковых команд.

Решая задачу, нашли самый большой делитель двух данных чисел. В арифметике число, являющееся самым большим делителем, одновременно для нескольких делимых, называют наибольшим общим делителем.

Для определения наибольшего общего делителя, нужно придерживаться определенного порядка выполнения математических действий:

Выполним задание.

Определите НОД (наибольший общий делитель) 66 и 44.

Чтобы выполнить задание будем придерживаться рассмотренного алгоритма действий.

Определим компоненты, входящие в состав числового значения.

Значит:

66 | 2

33

Результат деления оканчивается нечетной цифрой, проверяем по признакам делимости на 3:

66 | 2

33 | 3

11

Мы получили простое числовое значение

66 | 2

33 | 3

11 | 11

 1

     В итоге вычислений – 1, разложение окончено.

Переходим ко второму известному значению.

1) Определим составляющие, входящие в состав:

Проверяем по признакам делимости. Данное числовое значение заканчивается четной цифрой, значит, оно делится на 2.

44 | 2

          22

Частное снова делится на 2:

          44 | 2    

          22 | 2

          11

В результате простое число, делим само на себя:

44 | 2    

22 | 2

11 | 11

1

Разложение окончено.

2) Выпишем компоненты обоих делимых, определим одинаковые:

66 = 2 × 3 × 11

44 = 2 ×2 × 11

3) Перемножим выделенные составляющие:

2 × 11=22

Выходит, что наибольший общий делитель – 22.

На письме, рядом с обозначением НОД в скобочках записывают делимые, для которых определяли наибольший общий делитель:

НОД (66;44) = 22.

Разберем задачу

Выпускники на праздник последнего звонка, приготовили цветы своим учителям. Они принесли 69 роз и 46 гладиолусов и разделили поровну между всеми учителями. Сколько учителей поздравили выпускники?

Зная, что цветы были поделены поровну, нам необходимо найти максимальную численность учителей,на которую можно разделить и розы и гладиолусы.

Для определения НОД данных делимых, воспользуемся алгоритмом вычисления:

1) Разложим на составляющие:

69 | 3               46 | 2

23 | 23             23 | 23

1                       1

2) Выберем общее числовое значение находящееся в составляющих :

69 = 3 × 23

46 = 2 × 23.

Нам подходит только  23.

НОД (69;46) = 23.

Наибольшим общим делителем для данных чисел будет 23. 

Выпускники поздравили 23 учителя.

Использование НОК для сложения и вычитания дробей

Теперь посмотрим, как можно использовать эти знания на практике, для решения задач. Используя второй ряд чисел составим три дроби, которые нужно сложить:

$${3\over18}; {4\over15}; {8\over25}$$

НОК=450, это мы уже посчитали в предыдущем пункте. Посмотрим, на какое число нужно домножить числитель и знаменатель каждой дроби, чтобы привести их к общему знаменателю.

${3\over18}$ нужно домножить на число, равное ${НОК\over18}={450\over18}=25$.

Домножим числитель и знаменатель дроби на 25:

$${3\over18}={{3*25}\over{18*25}}={75\over450}$$

Аналогично поступим с каждой из оставшихся дробей:

${4\over15}$ нужно домножить на ${НОК\over15}={450\over15}=30$

$${4\over15}={{4*30}\over{15*30}}={120\over450}$$

${8\over25}$ нужно домножить на ${НОК\over25}=18$

$${8\over25}={{8*18}\over{25*18}}={144\over450}$$

Теперь сложим получившиеся дроби:

$${3\over18}+{4\over15}+{8\over25}={75\over450}+{120\over450}+{144\over450}={339\over450}$$

Это и есть сумма ряда.

Что мы узнали?

Вы определили, что такое НОК, зачем он нужен и как его найти. Разобрали на примерах различные случаи нахождения НОК и решили задачу на сложение дробей с применением этого показателя.

1. /5

   Вопрос 1 из 5

Как проверить, что число делится на другое число без остатка?

Чтобы узнать, делится ли одно число на другое без остатка, можно воспользоваться некоторыми свойствами делимости чисел. Тогда, комбинируя их, можно проверять делимость на некоторые их них и их комбинации.

Некоторые признаки делимости чисел

1. Признак делимости числа на 2
Чтобы определить, делится ли число на два (является ли оно чётным), достаточно посмотреть на последнююю цифру этого числа: если она равна 0, 2, 4, 6 или 8, то число чётно, а значит делится на 2.Пример: определить, делится ли на 2 число .Решение: смотрим на последнюю цифру: 8 — значит число делится на два.

2. Признак делимости числа на 3
Число делится на 3 тогда, когда сумма его цифр делится на три. Таким образом, чтобы определить, делится ли число на 3, нужно посчитать сумму цифр и проверить, делится ли она на 3. Даже если сумма цифр получилась очень большой, можно повторить этот же процесс вновь.Пример: определить, делится ли число на 3.Решение: считаем сумму цифр: 3+4+9+3+8 = 27. 27 делится на 3, а значит и число делится на три.

3. Признак делимости числа на 5
Число делится на 5 тогда, когда его последняя цифра равна нулю или пяти.Пример: определить, делится ли число на 5.Решение: смотрим на последнюю цифру: 8 — значит число НЕ делится на пять.

4. Признак делимости числа на 9
Этот признак очень похож на признак делимости на тройку: число делится на 9 тогда, когда сумма его цифр делится на 9.Пример: определить, делится ли число на 9.Решение: считаем сумму цифр: 3+4+9+3+8 = 27. 27 делится на 9, а значит и число делится на девять.

Наибольший общий делитель (НОД)

Наибольший общий делитель (НОД) — нужен для сокращения дробей и быстрых вычислений.

Допустим, у тебя есть два числа: 12 и 8.

На какое наибольшее число делятся оба этих числа? Ты, не задумываясь, ответишь 4, потому что знаешь, что:

12 = 4 * 3 = 2 * 2 * 3

8 = 4 * 2 = 2 * 2 * 2

Какие цифры в разложении общие?

Правильно, 2 * 2 = 4. Вот и твой ответ был 4.

Держа в голове этот простой пример, ты не забудешь алгоритм, как находить НОД. 

Попробуй «выстроить» его у себя в голове. Получилось?

Чтобы найти НОД необходимо:

1. Разложить числа на простые множители (на такие числа, которые нельзя разделить ни на что больше, кроме самого себя или на 1, например, 3, 7, 11, 13 и т.д.).
2. Выписать множители, которые входят в состав обоих чисел.
3. Перемножить их.

Понимаешь, зачем нам нужны были признаки делимости? Чтобы ты посмотрел на число и мог начать делить без остатка.

Найдем НОД числа 290

Глядя на него, ты сразу можешь сказать, что оно делится на 10, запишем:

290 = 29 * 10

29 больше разделить ни на что нельзя, а вот 10 можно – 5 и 2, получаем:

290 = 29 * 5 * 2

Найдем НОД числа  485.

По признакам делимости оно должно без остатка делиться на 5, так как на 5 заканчивается. Делим:

485 = 5 * 97

Проанализируем изначальное число.

На 2 оно делиться не может (последняя цифра – нечетная),85 – не делится на 4, значит число тоже не делится на 4,На 3 и на 9 также не делится (сумма цифр, входящих в число, не делится на 3 и на 9)На 6 тоже не делится, так как не делится на 2 и 3,На 8 тоже не делится, так как не делится на 2 и 4.97 нельзя разделить на 7 нацело,

Значит, число 485 можно разложить только на 5 и 97.

А теперь найдем НОД этих чисел (290 и 485).

Какое это число?

Правильно, 5.

Отрицательные числа – «лжечисла» и их признание человечеством

Как ты уже понял, это числа, противоположные натуральным, то есть:

−1; −2; −3; −4 и т.д.

Отрицательные числа можно складывать, вычитать, умножать и делить – все как в натуральных.

Казалось бы, что в них такого особенного?

А дело в том, что отрицательные числа «отвоевывали» себе законное место в математике аж до XIX века (до этого момента было огромное количество споров, существуют они или нет).

Само отрицательное число возникло из-за такой операции с натуральными числами, как «вычитание».

Действительно, из 3 вычесть 11 – вот и получается отрицательное число. Именно поэтому, множество отрицательных чисел часто называют «расширением множества натуральных чисел».

Отрицательные числа долго не признавались людьми.

Так, Древний Египет, Вавилон и Древняя Греция – светочи своего времени, не признавали отрицательных чисел, а в случае получения отрицательных корней в уравнении (например, как у нас 3−11), корни отвергались как невозможные.

Впервые отрицательные числа получили свое право на существование в Китае, а затем в VII веке в Индии.

Как ты думаешь, с чем связано это признание?

Правильно, отрицательными числами стали обозначать долги (иначе — недостачу).

Считалось, что отрицательные числа – это временное значение, которое в результате изменится на положительное (то есть, деньги кредитору все же вернут). Однако, индийский математик Брахмагупта уже тогда рассматривал отрицательные числа наравне с положительными.

В Европе к полезности отрицательных чисел, а также к тому, что они могут обозначать долги, пришли значительно позже, эдак, на тысячелетие.

Первое упоминание замечено в 1202 году в «Книге абака» Леонарда Пизанского (сразу говорю — к Пизанской башне автор книги отношения никакого не имеет, а вот числа Фибоначчи – это его рук дело (прозвище Леонардо Пизанского — Фибоначчи)).

Далее европейцы пришли к тому, что отрицательные числа могут обозначать не только долги, но и нехватку чего бы то ни было, правда, признавали это не все.

Так, в XVII веке Паскаль считал что 0−4=0.

Как думаешь, чем он это обосновывал?

Верно, «ничто не может быть меньше НИЧЕГО».

Отголоском тех времен остается тот факт, что отрицательное число и операция вычитания обозначается одним и тем же символом – минусом «-». И правда: 6−8. Число «8» положительное, которое вычитается из 6, или отрицательное, которое суммируется к 6?… Что-то из серии «что первое: курица или яйцо?» Вот такая вот, своеобразная эта математическая философия.

Отрицательные числа закрепили свое право на существование с появлением аналитической геометрии, иначе говоря, когда математики ввели такое понятие как числовая ось.

Именно с этого момента наступило равноправие. Однако все равно вопросов было больше чем ответов, например:

пропорция \( \displaystyle  \frac{1}{-1}=\frac{-1}{1}\)

Данная пропорция носит название «парадокс Арно». Подумай, что в ней сомнительного?

Давай рассуждать вместе «\( \displaystyle  1\)» больше, чем «\( \displaystyle  -1\)» верно? Таким образом, согласно логике, левая часть пропорции должна быть больше, чем правая, но они равны… Вот он и парадокс.

В итоге, математики договорились до того, что Карл Гаусс (да, да, это тот самый, который считал сумму \( \displaystyle  40\) (или \( \displaystyle  100\)) чисел) в 1831 году поставил точку.

Он сказал, что отрицательные числа имеют те же права, что и положительные, а то, что они применимы не ко всем вещам, ничего не означает, так как дроби так же не применимы ко многим вещам (не бывает так, что яму роют \( \displaystyle  1,5\) землекопа, нельзя купить \( \displaystyle  4,5\) билета в кино и т.д.).

Успокоились математики только в XIX веке, когда Уильямом Гамильтоном и Германом Грассманом была создана теория отрицательных чисел.

Наибольший общий делитель

Определение. Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.

Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа. Например, вместо переменной a подставим число 12, а вместо переменной b — число 9. Теперь попробуем прочитать это определение:

Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 12 и 9 делятся без остатка.

Из определения понятно, что речь идёт об общем делителе чисел 12 и 9. Причем делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.

Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.

Второй и третий способы довольны просты и дают возможность быстро найти НОД. Рассмотрим все три способа. А какой применять на практике — выбирать вам.

Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9.

Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.

12 : 1 = 12 (12 разделилось на 1 без остатка, значит 1 является делителем числа 12)

12 : 2 = 6 (12 разделилось на 2 без остатка, значит 2 является делителем числа 12)

12 : 3 = 4 (12 разделилось на 3 без остатка, значит 3 является делителем числа 12)

12 : 4 = 3 (12 разделилось на 4 без остатка, значит 4 является делителем числа 12)

12 : 5 = 2 (2 в остатке) (12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)

12 : 6 = 2 (12 разделилось на 6 без остатка, значит 6 является делителем числа 12)

12 : 7 = 1 (5 в остатке) (12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)

12 : 8 = 1 (4 в остатке) (12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)

12 : 9 = 1 (3 в остатке) (12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)

12 : 10 = 1 (2 в остатке) (12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)

12 : 11 = 1 (1 в остатке) (12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)

12 : 12 = 1 (12 разделилось на 12 без остатка, значит 12 является делителем числа 12)

Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9

9 : 1 = 9 (9 разделилось на 1 без остатка, значит 1 является делителем числа 9)

9 : 2 = 4 (1 в остатке) (9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)

9 : 3 = 3 (9 разделилось на 3 без остатка, значит 3 является делителем числа 9)

9 : 4 = 2 (1 в остатке) (9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)

9 : 5 = 1 (4 в остатке) (9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)

9 : 6 = 1 (3 в остатке) (9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)

9 : 7 = 1 (2 в остатке) (9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)

9 : 8 = 1 (1 в остатке) (9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)

9 : 9 = 1 (9 разделилось на 9 без остатка, значит 9 является делителем числа 9)

Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:

Выписав делители, можно сразу определить какой является наибольшим и общим.

Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3

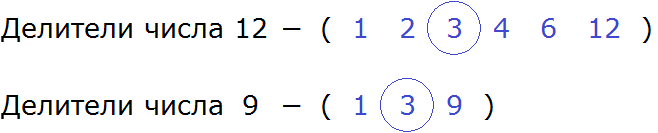
И число 12 и число 9 делятся на 3 без остатка:

Значит НОД (12 и 9) = 3