Делимость чисел. признак делимости

Признак делимости на $9$

Замечание 9

Если сумма цифр целого числа делится на $9$, то и само число делится на $9$, в других случаях число на $9$ не делится.

Пример 7

Проверить, делится ли число $675$ на $9$.

Решение.

Найдем сумму цифр числа $675=6+7+5=18$. Т.к. полученная сумма $18$ делится на $9$, то по признаку делимости на $9$ число $675$ делится на $9$.

Ответ: $675⋮9$.

Пример 8

Проверить, делится ли число $1 \ 893$ на $9$.

Решение.

Найдем сумму цифр числа $1 \ 893 = 1 + 8 + 9 + 3 = 21$. Т.к. полученная сумма $21$ не делится на $9$, то по признаку делимости на $9$ число $1 \ 893$ не делится на $9$.

Ответ: $1 \ 893$ не делится на $9.$

Признаки делимости

Замечание 1

Признаки делимости применяются к числам с целью определить, делится ли заданное целое число a на целое положительное число $b$ без непосредственного проведения деления $a$ на $b$.

Замечание 2

Признаки делимости обычно применяют не к самому числу, а к числам, состоящим из цифр, которые участвуют в записи этого числа.

Признаки делимости на числа $2, 5$ и $10$ позволяют проверить делимость числа по одной лишь последней цифре числа.

Другие признаки делимости предполагают проведение анализа двух, трех или больше последних цифр числа. Например, признак делимости на $4$ требует анализа двузначного числа, которое составлено из двух последних цифр числа; признак делимости на 8 требует анализа числа, которое образовано тремя последними цифрами числа.

При использовании других признаков делимости необходимо проанализировать все цифры числа. Например, при использовании признака делимости на $3$ и признака делимости на $9$ необходимо найти сумму всех цифр числа, а затем проверить делимость найденной суммы на $3$ или на $9$ соответственно.

Признаки делимости на составные числа объединяют несколько других признаков. К примеру, признак делимости на $6$ представляет собой объединение признаков делимости на числа $2$ и $3$, а признак делимости на $12$ – на числа $3$ и $4$.

Применение некоторых признаков делимости требует проведения значительной вычислительной работы. В таких случаях может оказаться проще выполнить непосредственное деление числа $a$ на $b$, которое приведет к решению вопроса, можно ли разделить данное число $a$ на число $b$ без остатка.

§ 1. Делимость чисел.

1. Делители и кратные.

20 яблок можно разделить поровну между 4 ребятами. Каждый получит по 5 яблок. А если надо разделить (не разрезая) 20 яблок между 6 ребятами, то каждый получит по 3 яблока, а ещё 2 яблока останутся. Говорят, что число 4 является делителем числа 20, а число 6 не является делителем числа 20.

Делитель натурального числа. Делителем натурального числа а называют натуральное число, на которое а делится без остатка.

Число 12 имеет шесть делителей: 1, 2, 3, 4, 6 и 12.Число 1 является делителем любого натурального числа.

Пусть на столе лежат пачки, в каждой из которых по 8 печений. Не раскрывая пачек, можно взять 8 печений, 16 печений, 24 печенья, а 18 печений так взять нельзя. Числа 8, 16, 24 делятся на 8, а 18 на 8 не делится. Говорят, что числа 8, 16, 24 кратны числу 8, а число 18 не кратно числу 8.

Кратное натурального числа. Кратным натурального числа а называют натуральное число, которое делится без остатка на а.

Любое натуральное число имеет бесконечно много кратных. Например, первые пять чисел, кратных 8, такие: 8, 16, 24, 32, 40. Наименьшим из кратных натурального числа является само это число.

ВОПРОСЫ:Какое число называют делителем данного натурального числа? Какое число называют кратным натуральному числу а? Какое число является делителем любого натурального числа? Какое число и кратно n, и является делителем n?

2. Признаки делимости на 10, на 5 и на 2.

Всякое натуральное число, запись которого оканчивается цифрой 0, делится без остатка на 10. Чтобы получить частное, достаточно отбросить эту цифру 0.

Например, 280 делится без остатка на 10, так как 280 : 10 = 28.

При делении же числа 283 на 10 получаем неполное частное 28 и остаток 3 (т. е. последнюю цифру записи этого числа). Поэтому если последняя цифра в записи натурального числа отлична от нуля, то это число не делится без остатка на 10.

Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10. Если запись натурального числа оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа.

Число 10 = 2 • 5. Поэтому число 10 делится без остатка и на 2, и на 5. Отсюда и любое число, запись которого оканчивается цифрой 0, делится без остатка и на 5, и на 2.

Например, 60 = 6 • 10 = 6 • (2 • 5) = (6 • 2) • 5 = 12 • 5, значит, 60 : 5 = 12. А из того, что 60 = 6 • (5 • 2) = (6 • 5) • 2 = = 30-2, получаем, что 60 : 2 = 30.

Каждое число можно представить в виде суммы полных десятков и единиц, например: 246 = 240 + 6, 1435 = = 1430 + 5. Так как полные десятки делятся на 5, то и всё число делится на 5 лишь в том случае, когда на 5 делится число единиц. Это возможно только тогда, когда в разряде единиц стоит цифра 0 или 5.

Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5. Если же запись числа оканчивается иной цифрой, то число без остатка на 5 не делится.

Например, числа 870 и 875 делятся без остатка на 5, а числа 872 и 873 на 5 без остатка не делятся.

Числа, делящиеся без остатка на 2, называют чётными, а числа, которые при делении на 2 дают остаток 1, называют нечётными. Из однозначных чисел числа 0, 2, 4, 6 и 8 чётны, а числа 1, 3, 5, 7 и 9 нечётны. Поэтому и цифры О, 2, 4, 6, 8 называют чётными, а цифры 1, 3, 5, 7, 9 — нечётными. Все полные десятки делятся на 2 без остатка (т. е. они чётны). Значит, любое натуральное число чётно лишь в случае, когда в разряде единиц стоит чётная цифра, и нечётно, когда в разряде единиц стоит нечётная цифра.

Если запись натурального числа оканчивается чётной цифрой, то это число чётно (делится без остатка на 2), а если запись числа оканчивается нечётной цифрой, то это число нечётно.

Например, числа 2, 60, 84, 96, 308 чётные, а числа 3, 51, 85, 97, 509 нечётные.

ВОПРОСЫ:Как по записи натурального числа определить, делится оно без остатка на 10 или не делится на 10? Как по записи натурального числа узнать, делится оно без остатка на 5 или не делится на 5? Как по записи натурального числа узнать, делится оно без остатка на 2 или не делится на 2?

5. Разложение на простые множители.

Число 210 является произведением чисел 21 и 10. Значит, 210 = 21 • 10. Числа 21 и 10 составные. Их тоже можно представить в виде произведений: 21 = 3 • 7, 10 = 2 • 5. Получаем: 210 = 3 • 7 • 2 • 5. Теперь в произведении 3 • 7 • 2 • 5 все множители — простые числа.

Проектные задачи.

Вы смотрели: Математика 6 класс УЧЕБНИК 2021 в 2-х частях (УМК Виленкин и др.) §1 Делимость чисел (Делители и кратные. Признаки делимости на 10, на 5 и на 2. Признаки делимости на 9 и на 3. Простые и составные числа. Разложение на простые множители. Наибольший общий делитель. Взаимно простые числа. Наименьшее общее кратное).

Это интересно

Древнегреческий философ (профессиональный мыслитель), математик и мистик (верил в существование сверхъестественных сил) Пифагор Самосский, чётные числа считал женскими, а нечётные — мужскими

На рисунке числа от 1 до 100 (чётные и нечётные числа разного цвета)

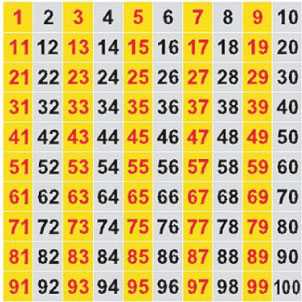
В старину люди верили в магию чисел, где всё хорошее ассоциировалось с нечётными цифрами, а плохое – с чётными. Поэтому, например, в Рождество на стол всегда ставили нечётное количество блюд. Люди верили, что нечётные числа символизируют постоянное продолжение жизни, незавершенность. А чётные, наоборот, означают конечность всего живого, остановку движения.

Что такое множество в математике и как оно обозначается

Множество – это количество предметов или чисел, обладающих общими свойствами.

Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.

В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д.

Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a1, a2 и т. д.

Границы совокупности обозначаются фигурными скобками { }.

Пример:

1. А = {а, в, с, у} – А состоит из четырех элементов.
2. Записать совокупность Z согласных букв в слове «калькулятор»:

Z = {к, л, т, р}, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.

Принадлежность элементов множеству обозначается знаком – Є.

Пример: N = {a, b, c, y}, а Є N – элемент «а» принадлежит N.

Выделяют три вида множеств:

• конечные — совокупности, имеющие максимальный и минимальный предел (например, отрезок);
• бесконечные — не являющиеся конечными (например, числовые);
• пустые (обозначаются Ø) – не имеющие элементов.

Если две разные совокупности содержат одинаковые элементы, то одна из них (со всеми своими элементами) является подмножеством другой и обозначается знаком — ⊆.

Пример: А = {а, в, с, у} и В = {а, в, с, е, к} – все элементы А являются элементами совокупности В, следовательно А ⊆ В.

Если множества состоят из одинаковых элементов, их называют равными.

Пример: А = {23, 29, 48} и В = {23, 29, 48}, тогда А = В.

В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.

Обозначения

Множество чаще всего обозначают заглавными буквами латинского алфавита, а его элементы — строчными. При этом элементы заключаются в фигурные скобки.

Например, если наших друзей зовут Том, Джон и Лео, то мы можем задать множество друзей, элементами которого будут Том, Джон и Лео.

Обозначим множество наших друзей через заглавную латинскую букву F (friends), затем поставим знак равенства и в фигурных скобках перечислим наших друзей:

F = { Том, Джон, Лео }

Пример 2. Запишем множество делителей числа 6.

Обозначим через любую заглавную латинскую букву данное множество, например, через букву D

D

затем поставим знак равенства и в фигурных скобках перечислим элементы данного множества, то есть перечислим делители числа 6

D = { 1, 2, 3, 6 }

Если какой-то элемент принадлежит заданному множеству, то эта принадлежность указывается с помощью знака принадлежности ∈. К примеру, делитель 2 принадлежит множеству делителей числа 6 (множеству D). Записывается это так:

2 ∈ D

Читается как «2 принадлежит множеству делителей числа 6»

Если какой-то элемент не принадлежит заданному множеству, то эта не принадлежность указывается с помощью зачёркнутого знака принадлежности ∉. К примеру, делитель 5 не принадлежит множеству D. Записывается это так:

5 ∉ D

Читается как «5 не принадлежит множеству делителей числа 6»

Кроме того, множество можно записывать прямым перечислением элементов, без заглавных букв. Это может быть удобным, если множество состоит из небольшого количества элементов. Например, зададим множество из одного элемента. Пусть этим элементом будет наш друг Том:

{ Том }

Зададим множество, которое состоит из одного числа 2

{ 2 }

Зададим множество, которое состоит из двух чисел: 2 и 5

{ 2, 5 }

Множество натуральных чисел

К совокупности натуральных чисел (N) относятся цифры, используемые при счете — от 1 до бесконечности.

Натуральные числа используют для исчисления порядка предметов. Обязательное условие данной числовой группы — каждое следующее число больше предыдущего на единицу.

N = {9, 11, 13, 15……}.

Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.

Множество целых чисел

Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:

Z = {-112, -60, -25, 0, 36, 58, 256}.

Следовательно, N — подмножество Z, что можно записать как N ⊆ Z. Любое натуральное число можно назвать так же и целым.

Множество рациональных чисел

Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:

Q={-½; 0; ½, 5; 10}.

Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:

5 = 5/1 = 10/2 = 25/5;

0,45 = 45/100 = 9/20.

Следовательно, N и Z являются подмножествами Q.

Делители от 11 и выше

Чтобы получилось деление на 11, необходимо сложить четные по счету номера, а затем нечетные, затем произвести вычитание. Если в процессе вычислений получился ноль или одиннадцать, то остатка не будет.

Онлайн-задание с ответом: 7535, 74019 и 50486.

Нечетные в первом случае 7 и 3, четные 5 и 5. Считаем:

• 7+3=10,
• 5+5=10,
• 10−10=0.

Четные во втором примере 4 и 1, нечетные — 7, 0, 9. Вычисление:

• 7+0+9=16.
• 4+1=5.
• 16−5=11.

В третьем примере нечетные 5, 4, 6, четные 0 и 8. Решаем:

• 5+4+6=15.
• 0+8=8.
• 15−8=7.

Ответ: в первом и втором примере десятых, сотых, тысячных и так далее не останется, а в третьем — останется.

Чтобы разделить на двузначный делитель 12, нужно произвести общие вычисления, характерные для делителей 3 и 4 одновременно. К примеру, 900 и 3432. Сначала следует разложить на слагаемые 9+0+0=9, значит, можно поделить на 3. В конце стоит два нуля — можно делить на 4. Проверка: 900:12=75. Первая часть задания решена, теперь делаем вторую: 3+4+3+2=12, 12:3=4. Таким образом проверяется кратность трем. Теперь четырем: в конце стоит 32, что указывает на кратность 4, значит, остатка не будет. Таким образом, оба примера кратны 12.

Дробь, кратная 13, разрешится без остатка, если последнюю цифру умножить на 4, после чего сложить число и последнюю цифру. Если полученная сумма кратна 13 или равно 0, то деление получится.

Например, 6942:

• 2*4=8.
• 694+8=702.
• 702:13=54.

Еще пример — 754:

• 4*4=16.
• 75+16=91.
• 91:13=7.

Дроби с кратными от 1 до 5

На единицу делится любое целое число.

Самым простым правилом является делимость на число два: если натуральное число оканчивается на четную цифру, то оно кратно двум. Если в конце стоит нечетная цифра, какими являются 1, 3, 5, 7, 9, то число на два не делится. То есть чтобы поделить многозначное число на два, в конце числа должна стоять одна из таких цифр: 2, 4, 6, 8, 0.

Пример: 6942 является четным, поскольку в конце четная цифра, поэтому оно кратно двум; число 19678456 также кратно двум, так как в конце стоит четная цифра 6. А вот число 6796345 не делится на 2, поскольку оно нечетное. Также нельзя получить ответ без остатка с такой суммы, как 398573 по этой же причине.

Деление на три имеет свое правило: нужно сложить все цифры, а затем проверить, делится ли сумма на три. Если да, то и данность разделится на три. Если нет, значит, не делится.

Например, возьмем 3576. Складываем 3+5+7+6=21. Полученную сумму 21 делим на три, получается семь. Значит, оно кратно трем без остатка. Проведем разложение шестизначного номера 353388. Оно раскладывается на три, поскольку сумма равна тридцати (3+5+3+3+8+8=30). Еще возьмем, например, 5819. Складываем: 5+8+1+9=23, полученная сумма не делится на три без остатка. Также и 2947 невозможно разделить, поскольку остаются тройки.

Например, 1000 делится на четыре, поскольку в конце 00. Делится также и 3824, так как в конце 24, которое кратно этому делителю. А вот 2986 не делится на четыре, так как 86 не кратно четырем, и 29087 тоже не может остаться целым, поскольку с 87 нельзя произвести расчета. Еще пример: четырехзначный номер 2648 можно разделить на этот делитель, так как 48:4=12.

Довольно простым правилом является делимость на пять. Частное получается без остатка, если в конце заданного числа стоит 5 или 0. Если оно не заканчивается одной из этих цифр, то при делении возникнет остаток.

Проверим правило, взяв пятизначное число 45765. Оно кратно пяти без остатка, так как заканчивается на пять. Также 45030 можно разделить, поскольку в конце ноль. А вот четырехзначное число 4321 без остатка не делится.

Признак делимости на $3$

Замечание 5

Если сумма цифр целого числа делится на $3$, то и само число делится на $3$, в других случаях число на $3$ не делится.

Пример 2

Проверить, делится ли число $123$ на $3$.

Решение.

Найдем сумму цифр числа $123=1+2+3=6$. Т.к. полученная сумма $6$ делится на $3$, то по признаку делимости на $3$ число $123$ делится на $3$.

Ответ: $123⋮3$.

Пример 3

Проверить, делится ли число $58$ на $3$.

Решение.

Найдем сумму цифр числа $58=5+8=13$. Т.к. полученная сумма $13$ не делится на $3$, то по признаку делимости на $3$ число $58$ не делится на $3$.

Ответ: $58$ не делится на $3$.

Иногда для проверки делимости числа на 3 нужно несколько раз применить признак делимости на $3$. Обычно такой подход используется в случае применения признаков делимости к очень большим числам.

Пример 4

Проверить, делится ли число $999 \ 675 \ 444$ на $3$.

Решение.

Найдем сумму цифр числа $999 \ 675 \ 444 = 9 + 9 + 9 + 6 + 7 + 5 + 4 + 4 + 4 = 27 + 18 + 12 = 57$. Если по полученной сумме сложно сказать, делится ли она на $3$, нужно еще раз применить признак делимости и найти сумму цифр полученной суммы $57=5+7=12$. Т.к. полученная сумма $12$ делится на $3$, то по признаку делимости на $3$ число $999 \ 675 \ 444$ делится на $3$.

Ответ: $999 \ 675 \ 444 ⋮3$.

Кратные числа

Если какое-нибудь число без остатка разделилось на другое, то его называют кратным этого числа. Например, 6 без остатка делится на 3. Поэтому 6 является кратным числа 3

6 : 3 = 2

Определение. Кратным числа а называется число, которое делится без остатка на а.

Данное определение содержит переменную a. Подставим вместо этой переменной любое число, например число 5 и прочитаем определение:

Кратным числа 5 называется число, которое делится без остатка на 5.

У любого числа бесконечно много кратных. Например, первыми кратными числа 5, являются числа 5, 10, 15, 20, 25. Все они кратны 5, поскольку делятся на 5 без остатка:

5 : 5 = 110 : 5 = 215 : 5 = 320 : 5 = 425 : 5 = 5

Признак делимости на 4

Двузначное число

Число делится на 4 тогда и только тогда, когда сумма удвоенной цифры в разряде его десятков и цифры в разряде единиц, также, делится на четыре.

• 64 – делится на 4, т. к. 6⋅2+4=16, а 16:4=4. 35 – не делится на 4, т. к. 3⋅2+5=11, а.

Число разрядов больше 2

Число кратно 4, когда две его последние цифры образуют число, делящееся на четыре.

• 344 – делится на 4, т. к. 44 кратно 4 (по алгоритму выше: 4⋅2+4=12, 12:4=3). 5219 – не кратно 4, т. к. 19 не делится нацело на 4.

Примечание:

Число делится на 4 без остатка, если:

• в его последнем разряде стоят цифры 0, 4 или 8, а предпоследний разряд при этом является четным; в последнем разряде – 2 или 6, а в предпоследнем – нечетные цифры.

Делимость на 11

Алгебра весьма облегчает отыскание признаков, по которым можно заранее, не выполняя деления, установить, делится ли данное число на тот или иной делитель. Признаки делимости на 2, 3, 4, 5, 6, 8, 9, 10 общеизвестны. Выведем признак делимости на 11; он довольно прост и практичен.

Пусть многозначное число N имеет цифру единиц а, цифру десятков b, цифру сотен с, цифру тысяч d и т. д., т. е.

N = а + 10b + 100с + 1000d + ... = a + 10 (b + 10c + 100d + ...),

где многоточие означает сумму дальнейших разрядов. Вычтем из N число 11(b + 10с + 100d + …), кратное одиннадцати. Тогда полученная разность, равная, как легко видеть,

а - b - 10(c + 10d + ...),

будет иметь тот же остаток от деления на 11, что и число N. Прибавив к этой разности число ll(c + 10d + …), кратное одиннадцати, мы получим число

a - b + c + 10(d + ...).

также имеющее тот же остаток от деления на 11, что и число N. Вычтем из него число 11(d + …), кратное одиннадцати, и т. д. В результате мы получим число

a - b + c - d + ... = (а + с + ...) - (b + d + ...),

имеющее тот же остаток от деления на 11, что и исходное число N.

Отсюда вытекает следующий признак делимости на 11: надо из суммы всех цифр, стоящих на нечетных местах, вычесть сумму всех цифр, занимающих четные места; если в разности получится 0 либо число (положительное или отрицательное), кратное 11, то и испытуемое число кратно 11; в противном случае наше число не делится без остатка на 11.

Испытаем, например, число 87635064:

 8 + 6 + 5 + 6 = 25, 
 7 + 3 + 0 + 4 = 14, 
 25 - 14 = 11. 

Значит, данное число делится на 11.

Существует и другой признак делимости на 11, удобный для не очень длинных чисел. Он состоит в том, что испытуемое число разбивают справа налево на грани по две цифры в каждой и складывают эти грани. Если полученная сумма делится без остатка на 11, то и испытуемое число кратно 11, в противном случае — нет. Например, пусть требуется испытать число 528. Разбиваем число на грани (5/28) и складываем обе грани:

5 + 28 = 33. 

Так как 33 делится без остатка на 11, то и число 528 кратно 11:

528 : 11 = 48.

Докажем этот признак делимости. Разобьем многозначное число N на грани. Тогда мы получим двузначные (или однозначные*) числа, которые обозначим (справа налево) через а, b, с и т. д., так что число N можно будет записать в виде

N = a + 100b + 10000с + ... = a + 100(b + 100с + ...).

* ()

Вычтем из N число 99(b + 100с + …), кратное одиннадцати. Полученное число

а + (b + 100с + ...) = a + b + 100(с + ...)

будет иметь тот же остаток от деления на 11, что и число N. Из этого числа вычтем число 99(с + …), кратное одиннадцати, и т. д. В результате мы найдем, что число N имеет тот же остаток от деления на 11, что и число

а + b + с + ...

Математика 10 класс

• – Индивидуальные занятия
• – В любое удобное для вас время
• – Бесплатное вводное занятие

Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.

Коды баннеров проекта DPVA.ru

Начинка: KJR Publisiers

Консультации и техническая

поддержка сайта:

Zavarka Team

Проект является некоммерческим. �нформация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Свойства делителей от 6 до 10

Составное шесть состоит из произведения двух последовательных чисел — 2 и 3. Теория кратности такова: число 6 составное, поэтому необходимо, чтобы одновременно действовали два правила признака делимости. Нужно, чтобы число было кратно и двум, и трем сразу.

Например, проверке подвергаются трехзначные числа 756 и 168. Они четные, поэтому делятся на два. Теперь нужно сложить 7+5+6=18, становится ясно, что сумма 18 делится на 3. Число 165 при разложении на однозначные цифры с последующим сложением превращается в 12, которое может разделиться на три. Оба числа кратны одновременно 2 и 3, значит, кратны шести.

Определение отношения с делимостью на семь довольно сложное: число делится, если при удвоении последней цифры и полученной разности результат кратен семи или равен нулю.

Пример, трехзначное число 679 кратно 7. (Калькулятор выдал 97). Узнать можно так:

• 2*9=18.
• 67−18=49.
• 49:7=7.

Из примера видно, что удвоилось последнее число, затем получена разность, после чего — отношение-доказательство.

В классе было дано задание доказать, что число 497 делится на семь. Порядок решения:

• 2*7=14.
• 49−14=35.
• 35:7=5.

Свойство при делителе 9 похоже на правило с 3. Формула делимости на 9 довольно простая: сумма цифр должна быть кратна девяти. Маленький пример: из 46980 возможно получить целое, 4+6+9+8+0= 27. Получившаяся сумма кратна 9. Еще одно задание: найти отношение с использованием признака кратности 9 при делимом 29565. Рассуждение: 2+9+5+6+5=27. Полученная сумма может разделиться на девять.

Слайды и текст этой презентации

Слайд 2Признаки делимости чиселЦель этой работы – познакомиться с признаками делимости,

научиться определять делится число или нет не производя деление, применять

свои знания в решении математических задач, используя признаки делимости.Признаки делимости играют в математике большую роль. Зная признаки делимости можно некоторые задачи решать устно. Признаки делимости можно применить при делении, при сокращении дробей, при нахождении общего знаменателя.

Слайд 3Например:
найдите наибольшее четырехзначное число, все цифры которого различны и которое

делится на 2, 5, 9 и 11;сократите дробь:

259 1295 во время спортивного праздника его участники должны выстроиться в колонну по 18 человек в шеренге, а потом перестроиться по 12 человек в шеренге. Какое наименьшее число спортсменов нужно пригласить для участия в празднике? Это задания из заочной школы.

Рассмотрим несколько основных признаков деления

Слайд 5Признак делимости на 10 Если число оканчивается цифрой 0,

оно оканчивается цифрой 0567823980034670

Слайд 6Признак делимости на 5 Если число оканчивается одной из цифр

0 или 5, то оно делится на 5.Например: 7385 делится

на 5, т.к. оканчивается цифрой 59840 делится на 5, т.к. оканчивается цифрой 06748345592375

Слайд 7Признак делимости на 2 Если число оканчивается одной

из цифр 0,2,4,6,8, то оно делится на 2.0,

2, 4, 6, 8.Например: 532 делится на 2, т.к. оно оканчивается цифрой 267396820175694

Слайд 8Признак делимости на 9 Если сумма цифр числа делится

на 9, то и само число делится на 9

Например: 153 (1+5+3=9, 9 делится на 9, 153:9=17) 121 3589871210701

Слайд 9Признак делимости на 3 Если сумма цифр числа делится

на 3, то и само число делится на 3.Например:375 делится

на 3, т.к. 3+7=5=15 , 15 делится на 3, значит и 375 делится на 344336126793021

двумя последними цифрами. Например: 324 (324;

24:4=6) 325

Слайд 11Признак делимости на 7 Число делится на 7 тогда и

только тогда, когда результат вычитания удвоенной последней цифры из этого

числа без последней цифры делится на 7 (например, 259 делится на 7, так как 25 — (2 · 9) = 7 делится на 7). 458 не делится на 7, т.к.45-2 · 8=29 546 делится на7,т.к.54-6 · 2=42

Слайд 12Признак делимости на8
Число делится на 8 тогда и только тогда,

которое делится на 8.Например: 12000234024

Слайд 13Признак делимости на 11Число делится на 11 тогда и только

тогда, когда сумма цифр с чередующимися знаками делится на 11

(то есть 182919 делится на 11, так как 1 — 8 + 2 — 9 + 1 — 9 = -22 делится на 11678934 не делится на 11 т.к. 6-7+8-9+3-4=-1 565445 делится на 11 т.к. 5-6+5-4+4-5=0

Слайд 14Признак делимости на12Число делится на 12 тогда и только тогда,

когда оно делится на 3 и на 4.56424 делится на

12 т.к. 5+6+4+2+4=21 делится на три и 24 делится на 4678933 не делится на 12 т.к. 33 не делится на 4,хотя 6+7+8+9+3+3=36 делится на 3

Слайд 15Признак делимости на13
Число делится на 13 тогда и только тогда,

когда число его десятков, сложенное с учетверённым числом единиц, кратно

13 (например, 845 делится на 13, так как 84 + (4 · 5) = 104 делится на 13).

Слайд 16Признак делимости на 7
Число делится на 7 тогда и только

тогда, когда результат вычитания удвоенной последней цифры из этого числа

без последней цифры делится на 7 (например, 259 делится на 7, так как 25 — (2 · 9) = 7 делится на 7).

Слайд 17Признаки делимости на 14,15
Признак делимости на 14
Число делится на 14

тогда и только тогда, когда оно делится на 2 и

на 7.
Признак делимости на 15
Число делится на 15 тогда и только тогда, когда оно делится на 3 и на 5.

Слайд 18Признак делимости на 19
Число делится на 19 тогда и только

тогда, когда число его десятков, сложенное с удвоенным числом единиц,

кратно 19 (например, 646 делится на 19, так как 64 + (6 · 2) = 76 делится на 19).

Слайд 19Признак делимости на 23
Число делится на 23 тогда и только

тогда, когда число его сотен, сложенное с утроенным числом десятков,

кратно 23 (например, 28842 делится на 23, так как 288 + (3 х 42) = 414 продолжаем 4 + (3 х 14) = 46 очевидно делится на 23).

Слайд 20

Мы изучили очень много признаков делимости. Все их конечно изучить невозможно, но изученные нам точно пригодятся. Пока на уроках математики мы полученные знания не применяем, но задачи из заочной школы мы можем решить. Мы думаем, что некоторые признаки будут применяться чаще других, но и все они небесполезны.

цифры которого различны и которое делится на 2, 5, 9

и 11. Сократите дробь: 259 1295 (25-2х9 и 129-5х2)делятся на7 Во время спортивного праздника его участники должны выстроиться в колонну по 18 человек в шеренге, а потом перестроиться по 12 человек в шеренге. Какое наименьшее число спортсменов нужно пригласить для участия в празднике?

Понятие делимости

Признаки делимости чисел — это функции чисел, позволяющие определить, является ли число кратным делителю или нет.

Свойства делимости:

1. Все целые числа делятся на единицу.
2. Каждое ненулевое целое число делится на натуральное число, равное модулю данного целого числа.
3. Все натуральные числа являются делителями нуля.
4. Если целое число а делится на натуральное число b и абсолютное значение а меньше, чем b, то а равно нулю.
5. Если целое число a отлично от нуля и делится на натуральное число b, то абсолютное значение a не меньше b.
6. Единственным делителем единицы является сама единица.
7. Чтобы целое число а делилось на натуральное число b, необходимо и достаточно, чтобы абсолютное значение числа а делилось на b.
8. Если натуральные числа делятся друг на друга без остатка, то они равны.

Свойства делимости можно использовать для решения задач и доказательства теорем.

Четные числа — это числа, которые делятся на два: 0, 2, 4, 6, 8, 10, 12 и т д. Ноль относится и к четным числам.

Нечетные числа – это числа, которые не делятся на два: 1, 3, 5, 7, 9, 11, 13 и так далее