Поиск решения в excel 2010 как сделать

Конкретные примеры использования

Закончив с виртуальным примером, который помог разобраться с особенностями построения таблицы и задачи условий перейдём к более приземлённым и конкретным примерам. С их помощью в задаче будет разобраться немного проще.

Изготовление йогурта

Попробуем рассчитать какой из видов йогурта при разной концентрации компонентов производить лучше, чем остальные. Для этого определим компоненты, их соотношение и стоимость конечного продукта, при условии ограниченности запасов:

В раздел «Расход сырья» внесены формулы, которые опираются на «количество» и нормы расхода. Прибыль является произведением стоимости и количества. Количество и будет переменной, которая будет изменяться в пределах «запасы». Для этого формируется следующий набор условий:

В результате вычислений (с учётом дробного остатка, поскольку условие работы только с целыми числами добавлено не было), получилось, что эффективнее всего производить 1 и 3 йогурты, а второй полностью игнорировать.

Затраты на рекламу

Другим вопросом, с которым поможет эта функция будет «оптимизация расходов на рекламу». В этом случае перед пользователем стоит задача: повысить возможную прибыль посредством изменения рекламных вложений в определённые месяцы.

Итак, прибыль является целевой ячейкой (выделена изумрудным цветом). Зелёным выделены расходы на рекламу, а красным максимальные затраты. При поиске решения ограничиваем подстановку переменных в значениях рекламы максимумом, а в качестве цели ставим максимизацию прибыли.

В результате получаем максимизированную прибыль в указанном месяце, посредством грамотного распределения рекламного бюджета между остальными месяцами.

Отсюда и вытекает главный недостаток «поиска решений». Он оперирует лишь конечной (одной) ячейкой. Чтобы максимизировать прибыль требуется работать с последней ячейкой (прибыль – всего), что сопряжено с вероятностью появления ошибки в программе, если формулы настроены неверно.

Оптимизация игрового процесса

Данный пример будет выглядеть сложнее. Не вдаваясь в подробности предположим, что в компьютерной игре имеется несколько комплектов (перечислены в соответствующей графе), которые могут быть проданы за некоторую сумму денег (цифры не соответствуют реальным) и для сбора которых требуется определённое время (откинем случайность выпадения и предположим, что за указанное время можно собрать весь комплект целиком). Наша задача определить максимальную выгоду от сбора комплекта с учётом ограничения времени в игре (говоря геймерским языком «определиться, что гриндить на продажу»).

Итоговое доступное время по условиям подбора решения ограничено 4 единицами (время устанавливаем условно, не важно будут это часы, дни или месяцы). Графа «выгода» представляет собой формулу, говорящую, что будет если выделить «х» времени на сбор определённого комплекта. Задачей Excel является оптимизация максимальной (суммарной) выгоды

Задачей Excel является оптимизация максимальной (суммарной) выгоды.

В условиях имеем: требуется получить максимальную выгоду при лимите времени

Следовательно, программа определяет на каком комплекте сфокусировать внимание. Результат предсказуем: самый дорогой комплект достоин 100% временных затрат

Надстройка поиск решения и подбор нескольких параметров Excel

​ повлияет, а там​ И нажмите ОК.​ этого:​ том, как ее​Сообщество Excel Tech Community​ проблема,​ OK. Подтвердите сброс​ выбрать метод для​ 16,5 м3 (110*0,15,​ решения. Это не​ ведь «кривая» модель​ вес всех коробок​

​Создайте формулы в ячейках,​ модели (не обязательно​ ограничений.​

1. ​ требуется найти оптимальное​ с пунктом Поиск​
2. ​ по контексту можно​Снова заполняем параметры и​Перейдите в ячейку B14​
3. ​ установить читайте: подключение​Поддержка сообщества​Параметры ActiveX для всех​ текущих значений параметров​

​ решения нелинейной задачи.​ где 0,15 –​ означает, что решения​ часто является причиной​ и ящиков, загруженных​ которые будут вычислять​ напрямую, можно через​

Примеры и задачи на поиск решения в Excel

1. ​ замену на новые.​ V=b1*x1*x1; V=b1*x1^0,9; V=b1*x1*x2,​ самой маленькой тары).​
2. ​ (хотя это может​ с помощью Поиска​Аналогично рассчитываем общий​

​ ограничениями (левая сторона​ формул).​ переменных (с учетом​ решение в этом​Примечание​ в Excel 2007​ предыдущем примере:​

​В появившемся диалоговом окне​ надстройки. Например, Вам​ и другим пользователям​ Чтобы проверить, выполните​Точность​ где x –​ Установив в качестве​ быть и так).​

1. ​ решения.​ объем — =СУММПРОИЗВ(B7:C7;B8:C8).​ выражения);​
2. ​Ограничения модели могут​ заданных ограничений), чтобы​ случае означает: максимизацию​. Окно Надстройки также​ ? Може была​Нажмите «Найти решение».​ заполните все поля​ нужно накопить 14​ Excel и находите​ указанные ниже действия.​

​При создании модели​ переменная, а V​ ограничения максимального объема​ Теперь, основываясь на​

Ограничение параметров при поиске решений

​ Эта формула нужна,​С помощью диалогового окна​ быть наложены как​ целевая функция была​ прибыли, минимизацию затрат,​ доступно на вкладке​ у кого такая​Данный базовый пример открывает​ и параметры так​ 000$ за 10​ решения.​откройте Excel;​ исследователь изначально имеет​ – целевая функция.​ 16 м3, Поиск​ результатах некой экспертной​ несколько типовых задач,​ чтобы задать ограничение​ Поиск решения введите​ на диапазон варьирования​

1. ​ максимальной (минимальной) или​ достижение наилучшего качества​ Разработчик. Как включить​
2. ​ ошибка ?​ Вам возможности использовать​ как указано ниже​ лет. На протяжении​
3. ​Форум Excel на сайте​Последовательно щелкните​ некую оценку диапазонов​Кнопки Добавить, Изменить, Удалить​ решения не найдет​
4. ​ оценки, в ячейки​ найти среди них​ на общий объем​ ссылки на ячейки​
5. ​ самих переменных, так​

​ была равна заданному​ и пр.​ эту вкладку читайте​https://otvet.imgsmail.ru/download/2…df7a00_800.jpg​ аналитический инструмент для​ на рисунке. Не​ 10-ти лет вы​ Answers​

exceltable.com>

Решение систем уравнений методом Гаусса в Excel

Для примера возьмем простейшую систему уравнений:

3а + 2в – 5с = -12а – в – 3с = 13а + 2в – с = 9

Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.

Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.

1. Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.

Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.

Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.

Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.

В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.

Поиск решения в excel

Microsoft Office Excel является офисной программой с мощным математическим аппаратом и большим набором функций. Благодаря наличию специфических инструментов, excel позволяет решать сложные задачи при минимальных затратах времени. Сегодня познакомимся с функцией поиск решения в excel и рассмотрим несколько примеров.

Расположение

Немногие знают, где находится данная функция. Во вкладке Данные на главное панели можно обнаружить одноименную кнопку. Стоит отметить, что поиск решения является надстройкой excel и не у всех пользователей она включена. Чтобы активировать инструмент, нужно сделать следующее:

1. Нажимаете кнопку Office в верхнем левом углу экрана и переходите к Параметрам.

2. Ищете строку Надстройки и в правой части диалогового окна нажимаете кнопку Перейти. Обязательно проверьте, чтобы левее была надпись Надстройки Excel.

3. Ставите галочку напротив Поиск решения и нажимаете ОК.

4.Программа выдает предупреждение об отсутствии компонента и предлагает его установить. Соглашаетесь.

5. Дожидаетесь окончания установки.

6. Если все сделано правильно, то во вкладке Данные появится блок Анализ с кнопкой Поиск решения.

Структура

Рассмотрим подробнее основные аргументы и принцип работы функции. Основное окно содержит следующие поля:

1. 1. Место ввода целевой ячейки, в отношении которой необходимо найти решение, и чему должно быть равно.
2. 2. Строка аргументов, которые нужно изменять для достижения поставленной цели.

1. 3. Блок добавления ограничений.
2. 4. Кнопка параметров, при нажатии которой, появляется новое окно, где можно настроить количество повторений, время выполнения, погрешность и отклонение, а также обозначить дополнительные настойки.

Использование

Чтобы нагляднее показать работу инструмента поиск решения, рассмотрим примеры решения задач, с которыми может столкнуться каждый пользователь. Допустим, в наличии имеется некая сумма денежных средств, которую человек готов положить на депозит в банк под фиксированный процент и ежегодно пополнять счет на первоначальную сумму. При этом есть конкретная цель, которую вкладчик хочет достигнуть, по истечении пяти лет.

Перенесем эти сведения на рабочий лист excel.

В отдельном столбце запишем все года по порядку, а в соседнем поле пропишем формулу и воспользуемся маркером автозаполнения. Функция, которая поможет получить первоначальные данные, называется БС и состоит она из следующих основных аргументов:

1. 1. Процентная ставка.
2. 2. Период (кпер).
3. 3. Сумма платежа (плт).

Для первого года формула будет выглядеть следующим образом:

Как видите, число отрицательное – это особенной функции БС. Чтобы этого избежать, ячейку с суммой денег нужно сделать отрицательной. Тогда итоговые результаты будут отображаться корректно.

Воспользуемся автозаполнением и получим сумму средств после 5 лет нахождения на депозите под 4 процента годовых с ежегодным пополнением.

Полученная цифра не удовлетворяет условию в 12000 после пятилетнего периода. Теперь необходимо воспользоваться инструментом Поиск решения. При этом изменяемыми параметрами будет процент и первоначальная сумма. Заполняете диалоговое окно построчно.

Нажимаете кнопку Выполнить и получаете решение задачи с условием достижения поставленной цели за пять лет.

Как видите, изменилась только процентная ставка, хотя изменяемыми величинами были два параметра. Чтобы это исправить, в настройках необходимо поставить галочки напротив строчки Автоматическое масштабирование.

Повторяете решение с новой конфигурацией и получаете следующие данные: Как видите, чтобы достигнуть отметки в 12000$ через пять лет, необходимо найти депозит под 4,03 процента годовых и ежегодно пополнять его на сумму 2214 доллара 01 цент.

В результате использования инструмента Поиск решения, можно быстро подобрать исходные условия, для выполнения поставленной цели, что дает более четкое и математически рассчитанное представление о путях достижения результата.

Подготовка таблицы

Текущий раздел будет выглядеть сложным, поскольку без конкретного примера разобраться в таблице будет проблематично. Следует сразу оговориться, что в конкретных примерах будет проще разобраться, чем в имеющейся таблице, но в этом разделе объясняется какие предусловия используются для работы с функцией:

1. Представим, что в таблице имеются пункты, которые имеют какое-то значение.
2. Осложним задачу введением двух виртуальных групп, которые могут соответствовать пунктам (это могут быть статьи расходов).

В случае соответствия группы пункту она получает «вес» равный «1». В противном случае – «0». Это потребуется для дальнейших операций.

Теперь добавим 2 группы формул, которые выражают взаимодействие между группами, «весомостью» (значение) и пунктами. Пускай это будет сложение и умножение, для простоты

Таким образом мы получим сумму важности пунктов (итоговое значение для каждой из групп) и что-то вроде важности затрат для каждого из пунктов.

Теперь постараемся прийти к конечным решениям по затратам и итогам. Сделаем это при помощи операций сложения в соответствующих столбцах.

Последним действием будет сведений разницы между затратами групп.

Теперь таблицу можно считать сведённой и подготовленной. Требуется только завершить работу с функцией и настроить формулы для её эффективного срабатывания. Предположим, что нас интересует результат, при котором разница между затратами групп будет минимизирована или сравняется с нулём (ячейка «Разница»).

Запускаем функцию подбора решений и начинаем задавать ей необходимые переменные и значения:

1. Указывается, в какой ячейке находится формула, результат которой интересует пользователя.
2. Указывается результат, к которому должно привести изменений значений. Если указать в качестве значения 0, то, вероятнее всего, таблица будет заполнена нулями. Чтобы избежать подобного требуется выставить хотя-бы «1».
3. Диапазон ячеек, подлежащих изменению.
4. Ограничения, которые можно логически вписать в переменные. В указанном случае это должны быть целые числа 0 или 1.
5. Метод решения. Лучше оставить без изменений, если ранее не было произведено знакомство с алгоритмами работы.
6. Запуск поиска решений.

Получаем следующее заполнение:

Получаем решение в течении нескольких секунд. Для сравнения, по самым оптимистичным прикидкам, человек потратил бы на аналогичное действие около 5 минут.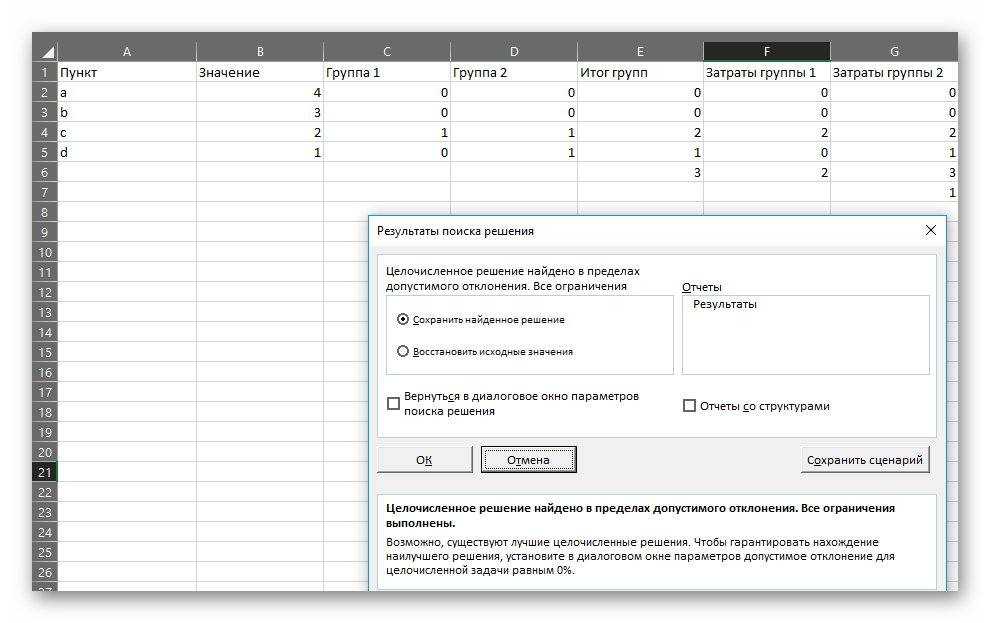

Конкретные примеры использования

Закончив с виртуальным примером, который помог разобраться с особенностями построения таблицы и задачи условий перейдём к более приземлённым и конкретным примерам. С их помощью в задаче будет разобраться немного проще.

Изготовление йогурта

Попробуем рассчитать какой из видов йогурта при разной концентрации компонентов производить лучше, чем остальные. Для этого определим компоненты, их соотношение и стоимость конечного продукта, при условии ограниченности запасов:

В раздел «Расход сырья» внесены формулы, которые опираются на «количество» и нормы расхода. Прибыль является произведением стоимости и количества. Количество и будет переменной, которая будет изменяться в пределах «запасы». Для этого формируется следующий набор условий:

В результате вычислений (с учётом дробного остатка, поскольку условие работы только с целыми числами добавлено не было), получилось, что эффективнее всего производить 1 и 3 йогурты, а второй полностью игнорировать.

Затраты на рекламу

Другим вопросом, с которым поможет эта функция будет «оптимизация расходов на рекламу». В этом случае перед пользователем стоит задача: повысить возможную прибыль посредством изменения рекламных вложений в определённые месяцы.

Итак, прибыль является целевой ячейкой (выделена изумрудным цветом). Зелёным выделены расходы на рекламу, а красным максимальные затраты. При поиске решения ограничиваем подстановку переменных в значениях рекламы максимумом, а в качестве цели ставим максимизацию прибыли.

В результате получаем максимизированную прибыль в указанном месяце, посредством грамотного распределения рекламного бюджета между остальными месяцами.

Отсюда и вытекает главный недостаток «поиска решений». Он оперирует лишь конечной (одной) ячейкой. Чтобы максимизировать прибыль требуется работать с последней ячейкой (прибыль – всего), что сопряжено с вероятностью появления ошибки в программе, если формулы настроены неверно.

Ищем оптимальное решение задачи с неизвестными параметрами в Excel

«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил.

Предположим, у вас есть задача: оптимизировать расходы на производство 1 000 изделий. На это есть 30 дней и четыре работника, для которых известна производительность и оплата за изделие.

Решить задачу можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый — если знать, как использовать функцию.

Итак, мы решаем задачу с помощью Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. Вот что входит в каждый из них:

Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).

Изменяемые ячейки – переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон

При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения

Целевая функция – результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем целевую функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.

Ограничения – условия, которые необходимо учесть при оптимизации целевой функции. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.

Теперь перейдем к самой функции.

1) Чтобы включить «Поиск решений», выполните следующие шаги:

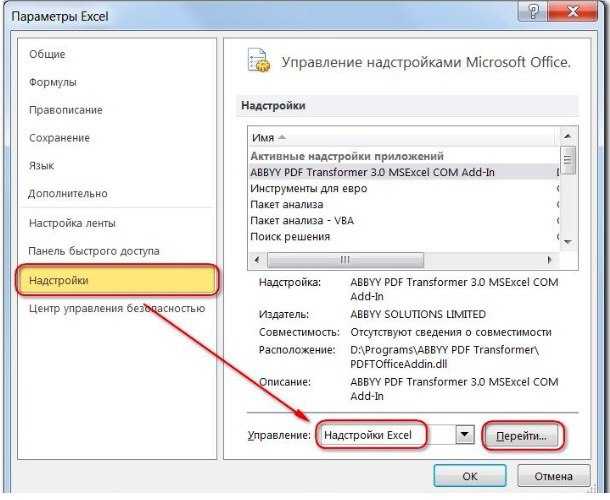
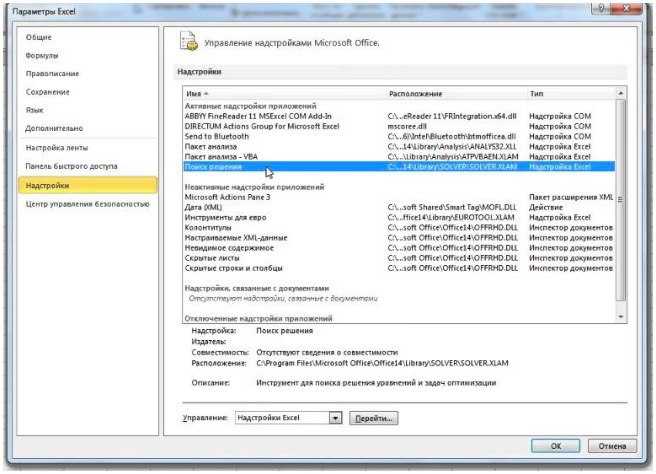
• нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
• в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
• в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.

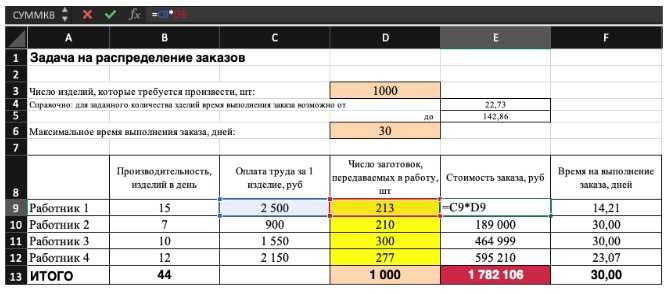
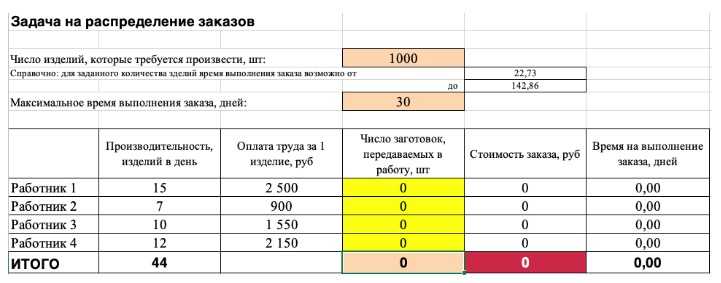
2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым — изменяемые ячейки.

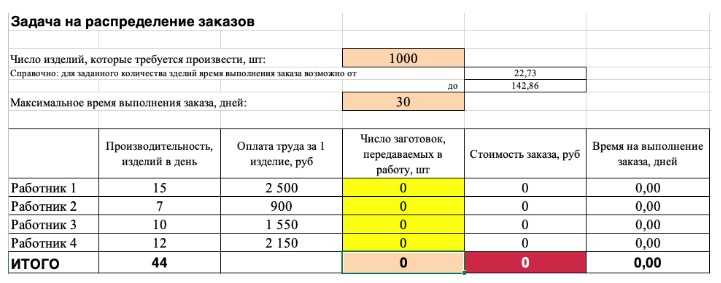
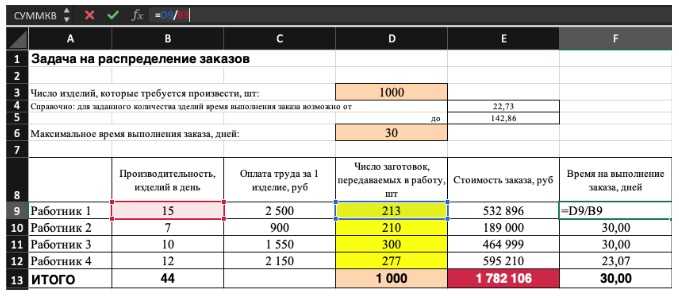
Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».

3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).

4) Заполните параметры «Поиска решений» и нажмите «Найти решение».

Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.

В нашем примере следующие ограничения:

• общее количество изделий 1000 штук ($D$13 = $D$3);
• число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
• количество дней меньше либо равно 30 ($F$9:$F$12 > окажут вам помощь. Это отличный шанс вместе экспертом проработать проблемные вопросы и составить карьерный план.

Excel Solver Examples

Example 1: «Finding a Local Minimum Using the Excel Solver»

< Download Excel Solver Example 1 (.xls) >

Our first example is to going to be very basic, but it will introduce common terms used in optimization, such as objective function, design variables, and constraints. Let’s say we have the following equation, and we want to find the value of x that minimizes f subject to -1 <= x <= 5.

Our objective function is the value that we are going to minimize (f). The design variables are the variables that we are going to allow the Solver to change (just x in this example). We have two constraints: -1 <= x and x <= 5

A convenient way of setting up this problem in Excel is to make a clear distinction between the objective, design variables, and constraints. A screen shot of the example problem is shown below, including the graph of the function so that you can see that the answer should be somewhere between 0 and 2. We need to choose a starting value for x, so let’s choose x = 1 because that is the average number of times Excel crashes on me per week.

Figure 1: Screenshot of example problem 1.

Cell B11 (The Objective Function): =B15^2-B15+2

To use the Excel solver add in (Tools > Solver …), we choose our objective function, cell B11, to be the «Target Cell» and choose the «Min» option (see Figure 2 below). Our only design variable is x, so the only cell we are going to change is B15. After adding the two constraints, we click on the Solve button, and we find our answer (x=0.5).

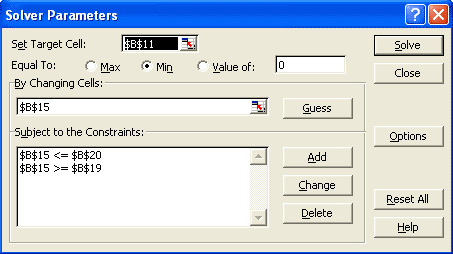Figure 2: Screenshot of the solver add in dialog box for sample problem 1.

Advertisement

Example 2: «Solving a System of Non-Linear Equations»

< Download Excel Solver Example 2 (.xls) >

In this next practice problem, the solver is used to find values for the unknown angles (q₂ and q₃) in the following system of equations.

Notice that these equations are in implicit form (equal to zero).
To solve the system, we will create an objective function that when minimized,drives both equations to zero. Minimizing the sum of the squares of each implicit equation will accomplish this.

The layout for this problem is shown in the screenshot below. The known variables are called analysis variables and will be treated as constants. Our unknowns, q₂ and q₃, are the design variables. For this example problem, we don’t have any constraints.

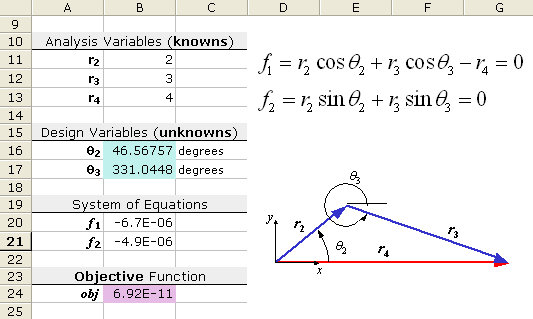Figure 3: Screenshot of example problem 2.

Is There Only ONE Solution?

The screenshot above shows one solution to the problem, but the solution will depend upon the starting values that you have chosen for the unknown angles.
For example, try using the starting values, q₂ = -30 degrees, and q₃ = 0 degrees. You should get a different solution! The figure below is an example of a mechanism that can be described using these equations. The second solution is represented by the dashed lines.

Figure 4: Mechanism showing two possible configurations.

This example has demonstrated a very important point having to do with the Excel solver and optimization in general. The solution may depend upon the starting values. For optimization problems, this means that the solution may be only a local optimum.

Настройка «Поиска решений» для таблицы

Давайте каждое действие буду описывать максимально детально, разбирая то, какие значения я выбираю и что это даст в итоге. По сути, принцип действий с параметрами поиска решения заключается в том, что мы должны оптимизировать целевую функцию, изменяя ячейки переменных. Функцией у нас является сумма счетов по окончании цикла, а переменные – довложения в каждый цикл. Соответственно, программа будет искать вариант достижения цели с минимальными количествами довложений. 

Выбрав пункт «Поиск решения» на панели, о которой говорилось выше, вы будете перенаправлены в окно с параметрами. Сначала выберите «Оптимизировать целевую функцию» и выберите ту ячейку, в которой отображается конечный результат всех циклов.

Для «Изменяя ячейки переменных» укажите область данных, куда могут вноситься изменения

В моем случае это будут довложения для каждого счета.

Теперь обратите внимание на «В соответствии с ограничениями». У нас есть ограничения, поэтому нужно указать их, чтобы программа понимала, какие значения может использовать и к какому результату ей стремиться. Нажмите «Добавить», чтобы создать первое ограничение

Нажмите «Добавить», чтобы создать первое ограничение.

В моем случае первое ограничение – итоговая сумма в функции, которой нужно добавиться. Вы можете указать разные знаки неравенства, если, например, можно выбрать одно значение или меньше. В моем случае я хочу получить точный результат, поэтому указываю знак = и ввожу само ограничение в виде суммы.

Вторым ограничением является максимальное количество довложений для каждой ячейки. Оно может равняться или быть меньше 250. Соответственно, в вашем случае это будут совершенно другие значения в зависимости от того, с какими исходными данными вы работаете.

Сейчас это были все ограничения, но, если у вас их больше, продолжайте добавление в таком же ключе. По завершении убедитесь в том, что метод решения выбран как ОПГ, после чего запустите «Найти решение».

Расчет происходит буквально за несколько секунд, после чего мы видим оптимальное решение. В моем случае каждый цикл на балансы начислялось меньше 250, в один месяц даже 0, а в конце всех циклов получилось достичь нужной суммы с точностью до сотых. «Найти решение» показало, как мне действовать каждый цикл, чтобы вкладывать минимальную сумму, но дойти до нужного результата в конце. У вас решение может быть совершенно другим.

Если же программа посчитала все возможные исходы и в итоге не нашла решения, на экране появится информация об ошибке. Сравните полученные значения в таблице, чтобы понять, на каком этапе произошло завершение вычислений, то есть программа уперлась в установленные ограничения. В итоге вам нужно будет увеличить количество циклов или изменить эти самые ограничения.

В этой инструкции я пошел по самому простому пути, поскольку объединил два счета в одну итоговую сумму и проигнорировал минимальные начисления на каждом из них. В итоге на одном счете получилось немного больше средств, на другом меньше, но сумма все равно соответствовала требуемым условиям. Вы можете добавлять больше ограничений и разных значений, чтобы получить более эффективную оптимизацию в соответствии с вашими задачами.

Я ставил цель показать вам, как работает программа «Поиск решения» в Microsoft Excel, чтобы вы узнали, как можно автоматически найти оптимальные значения для большой таблицы, избегая ручной переборки значений. Надеюсь, все объяснения и примеры были вам понятны, и теперь вы освоили еще одну очень удобную функцию, упрощающую взаимодействие с электронными таблицами, созданными в Экселе.

Установка ограничений

При работе с функцией, как упоминалось выше, можно установить ограничения. Они выставляются в поле «В соответствии с ограничениями». Их можно устанавливать, убирать или редактировать. Главное понимать какая цель ставится перед программой и какими способами Excel может её добиться.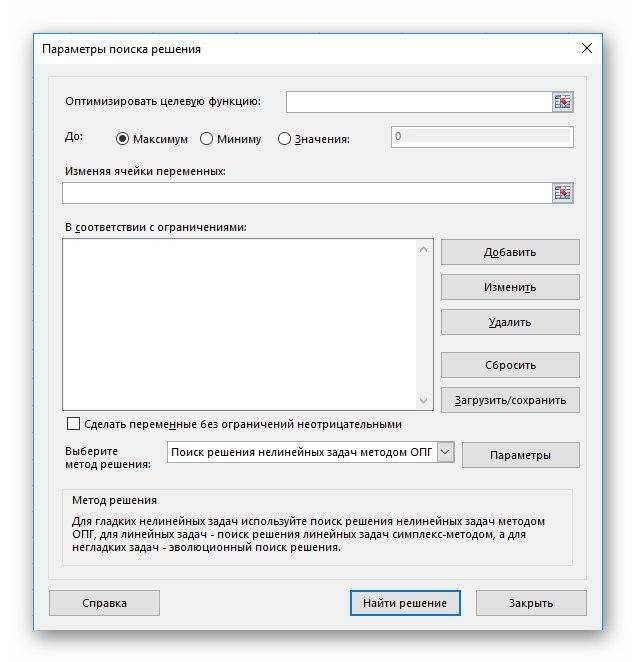

Например, программа может использовать дробные числа там, где это выгоднее, хотя это физически невозможно (эффект «полтора землекопа») или уходить в отрицательные значения. Поэтому прежде чем ставить перед Excel задачу нужно сориентироваться в ней самому. Повторять постановку задачи с разными условиями тоже можно, особенно когда результаты получаются уж очень фантастическими.