Использование поиска решений в excel 2010 для решения сложных задач

Функции программы Microsoft Excel: подбор параметра

Очень полезной функцией в программе Microsoft Excel является Подбор параметра. Но, далеко не каждый пользователь знает о возможностях данного инструмента. С его помощью, можно подобрать исходное значение, отталкиваясь от конечного результата, которого нужно достичь. Давайте выясним, как можно использовать функцию подбора параметра в Microsoft Excel.

Скачать последнюю версию Excel

• Суть функции
• Применение функции на практике
• Решение уравнений

Суть функции

Если упрощенно говорить о сути функции Подбор параметра, то она заключается в том, что пользователь, может вычислить необходимые исходные данные для достижения конкретного результата. Эта функция похожа на инструмент Поиск решения, но является более упрощенным вариантом.

Её можно использовать только в одиночных формулах, то есть для вычисления в каждой отдельной ячейке нужно запускать всякий раз данный инструмент заново.

Кроме того, функция подбора параметра может оперировать только одним вводным, и одним искомым значением, что говорит о ней, как об инструменте с ограниченным функционалом.

Применение функции на практике

Для того, чтобы понять, как работает данная функция, лучше всего объяснить её суть на практическом примере. Мы будем объяснять работу инструмента на примере программы Microsoft Excel 2010, но алгоритм действий практически идентичен и в более поздних версиях этой программы, и в версии 2007 года.

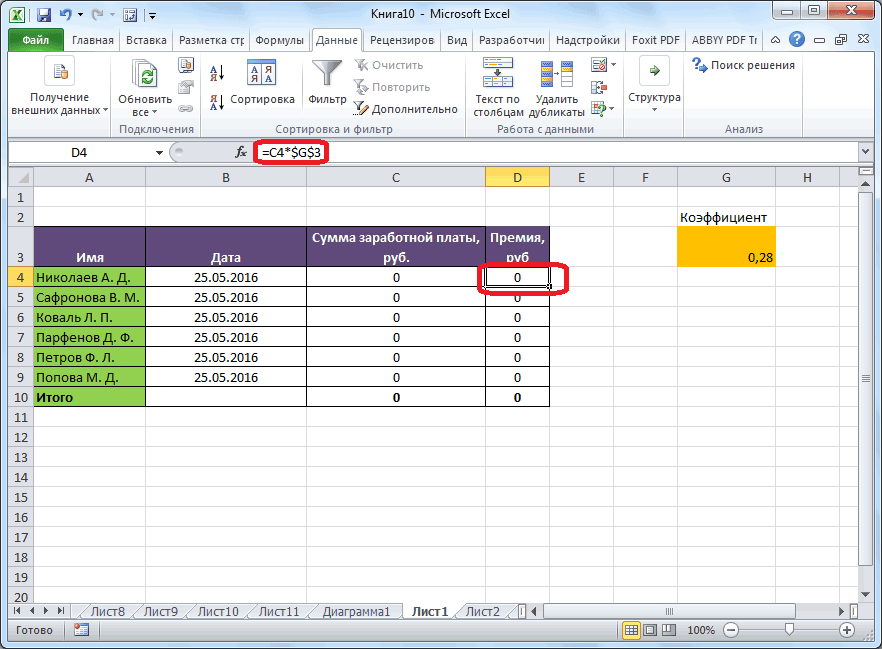
Имеем таблицу выплат заработной платы и премии работникам предприятия. Известны только премии работников. Например, премия одного из них — Николаева А. Д, составляет 6035,68 рублей. Также, известно, что премия рассчитывается путем умножения заработной платы на коэффициент 0,28. Нам предстоит найти заработную плату работников.

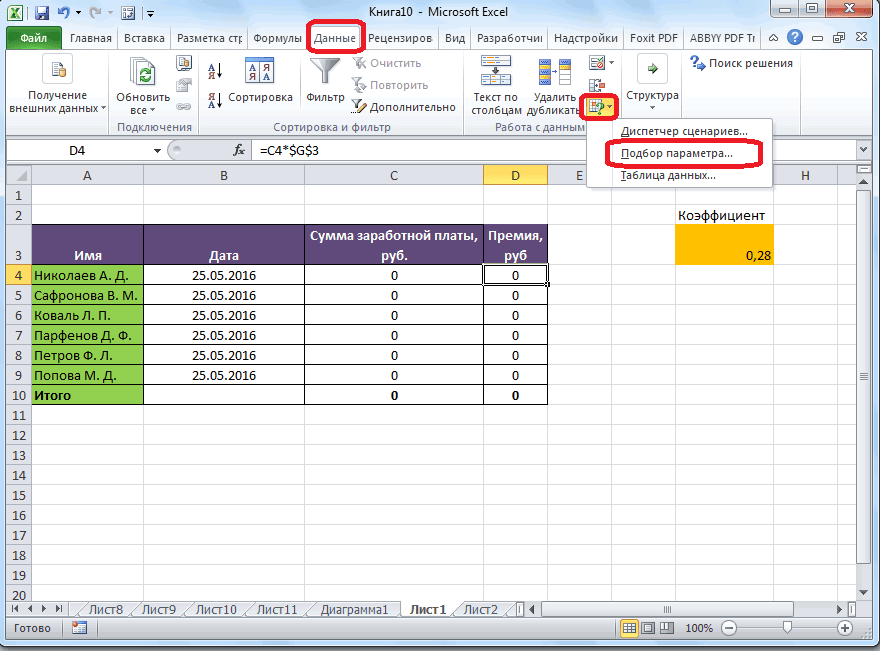
Для того, чтобы запустить функцию, находясь во вкладке «Данные», жмем на кнопку «Анализ «что если»», которая расположена в блоке инструментов «Работа с данными» на ленте. Появляется меню, в котором нужно выбрать пункт «Подбор параметра…».

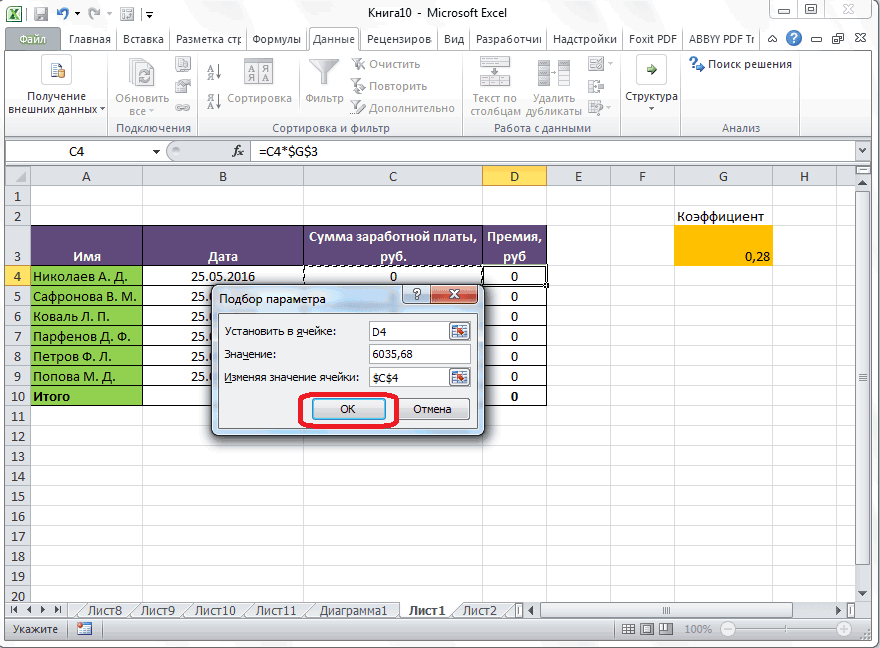
После этого, открывается окно подбора параметра. В поле «Установить в ячейке» нужно указать ее адрес, содержащей известные нам конечные данные, под которые мы будем подгонять расчет.

В данном случае, это ячейка, где установлена премия работника Николаева. Адрес можно указать вручную, вбив его координаты в соответствующее поле.

Если вы затрудняетесь, это сделать, или считаете неудобным, то просто кликните по нужной ячейке, и адрес будет вписан в поле.

В поле «Значение» требуется указать конкретное значение премии. В нашем случае, это будет 6035,68. В поле «Изменяя значения ячейки» вписываем ее адрес, содержащей исходные данные, которые нам нужно рассчитать, то есть сумму зарплаты работника. Это можно сделать теми же способами, о которых мы говорили выше: вбить координаты вручную, или кликнуть по соответствующей ячейке.

Когда все данные окна параметров заполнены, жмем на кнопку «OK».

Подобную операцию можно проделать и для других строк таблицы, если известна величина премии остальных сотрудников предприятия.

Решение уравнений

Кроме того, хотя это и не является профильной возможностью данной функции, её можно использовать для решения уравнений. Правда, инструмент подбора параметра можно с успехом использовать только относительно уравнений с одним неизвестным.

Допустим, имеем уравнение: 15x+18x=46. Записываем его левую часть, как формулу, в одну из ячеек. Как и для любой формулы в Экселе, перед уравнением ставим знак «=». Но, при этом, вместо знака x устанавливаем адрес ячейки, куда будет выводиться результат искомого значения.

В нашем случае, формулу мы запишем в C2, а искомое значение будет выводиться в B2. Таким образом, запись в ячейке C2 будет иметь следующий вид: «=15*B2+18*B2».

Запускаем функцию тем же способом, как было описано выше, то есть, нажав на кнопку «Анализ «что если»» на ленте», и перейдя по пункту «Подбор параметра…».

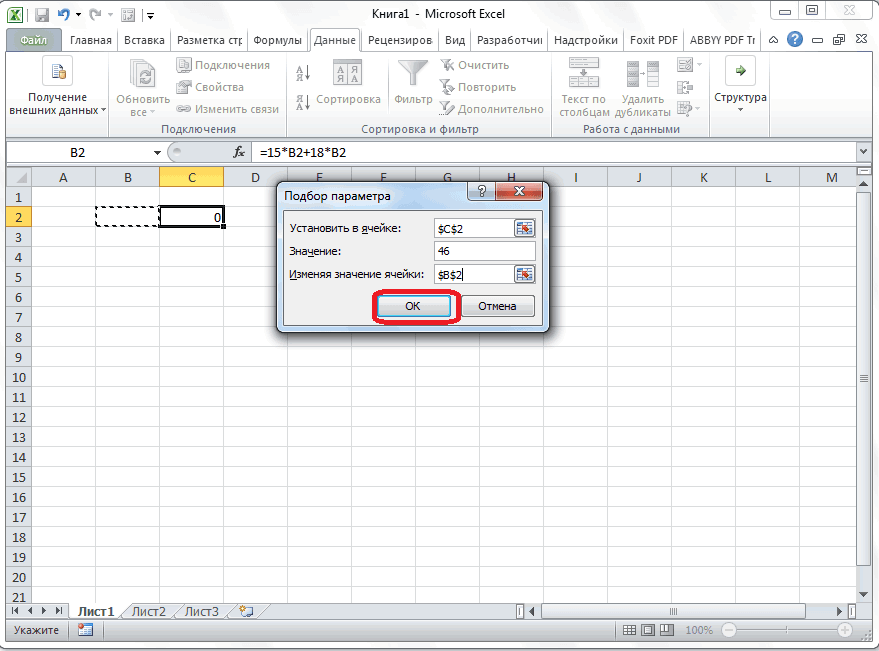
В открывшемся окне подбора параметра, в поле «Установить в ячейке» указываем адрес, по которому мы записали уравнение (C2).

В поле «Значение» вписываем число 45, так как мы помним, что уравнение выглядит следующим образом: 15x+18x=46.

В поле «Изменяя значения ячейки» мы указываем адрес, куда будет выводиться значение x, то есть, собственно, решение уравнения (B2). После того, как мы ввели эти данные, жмем на кнопку «OK».

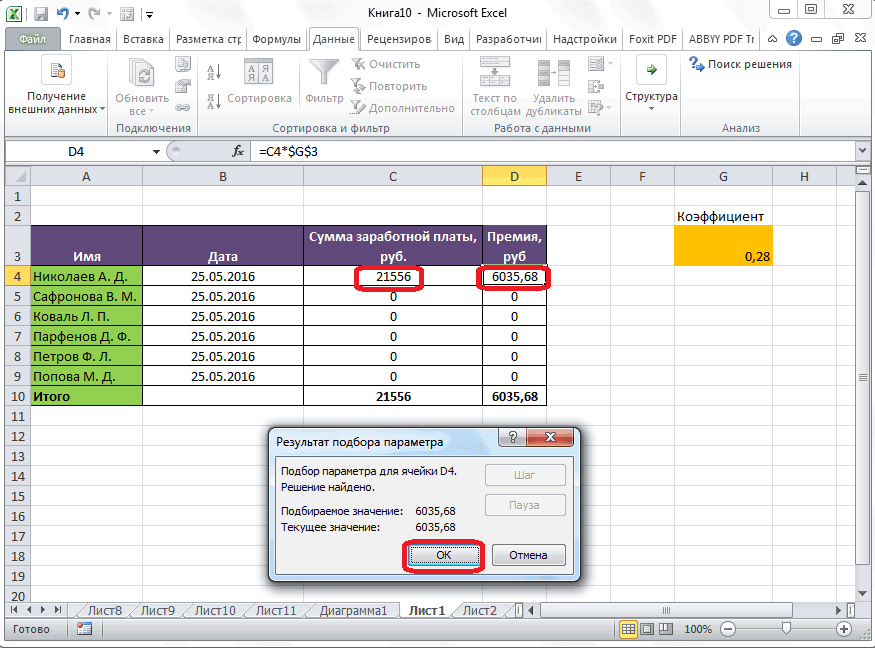
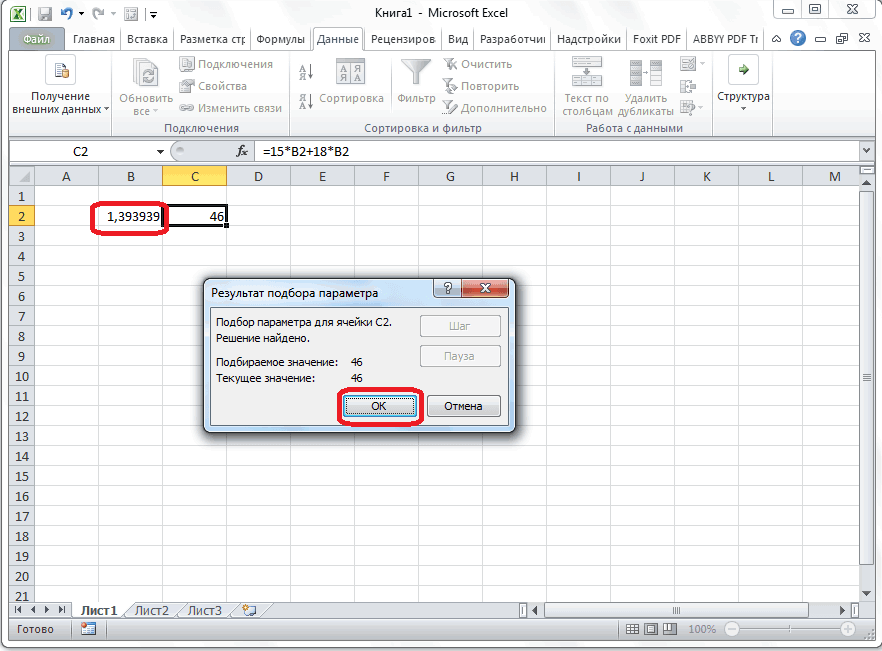
Как видим, программа Microsoft Excel успешно решила уравнение. Значение x будет равно 1,39 в периоде.

Изучив инструмент Подбор параметра, мы выяснили, что это довольно простая, но вместе с тем полезная и удобная функция для поиска неизвестного числа. Её можно использовать как для табличных вычислений, так и для решения уравнений с одним неизвестным.

Подбор параметра в MS EXCEL

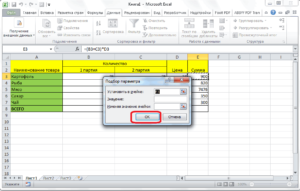
Обычно при создании формулы пользователь задает значения параметров и формула (уравнение) возвращает результат. Например, имеется уравнение 2*a+3*b=x, заданы параметры а=1, b=2, требуется найти x (2*1+3*2=8).

Инструмент Подбор параметра позволяет решить обратную задачу: подобрать такое значение параметра, при котором уравнение возвращает желаемый целевой результат X. Например, при a=3, требуется найти такое значение параметра b, при котором X равен 21 (ответ b=5).

 Подбирать параметр вручную – скучное занятие, поэтому в MS EXCEL имеется инструмент Подбор параметра.

В MS EXCEL 2007-2010 Подбор параметра находится на вкладке Данные, группа Работа с данным.

Простейший пример

Найдем значение параметра b в уравнении 2*а+3*b=x, при котором x=21, параметр а=3.

Подготовим исходные данные.

Значения параметров а и b введены в ячейках B8 и B9. В ячейке B10 введена формула =2*B8+3*B9 (т.е. уравнение 2*а+3*b=x). Целевое значение x в ячейке B11 введенодля информации.

Выделите ячейку с формулой B10 и вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…).

В качестве целевого значения для ячейки B10 укажите 21, изменять будем ячейку B9 (параметр b).

Нажмите ОК.

Инструмент Подбор параметра подобрал значение параметра b равное 5.

Конечно, можно подобрать значение вручную. В данном случае необходимо в ячейку B9 последовательно вводить значения и смотреть, чтобы х текущее совпало с Х целевым. Однако, часто зависимости в формулах достаточно сложны и без Подбора параметра параметр будет подобрать сложно.

Примечание: Уравнение 2*а+3*b=x является линейным, т.е. при заданных a и х существует только одно значение b, которое ему удовлетворяет. Поэтому инструмент Подбор параметра работает (именно для решения таких линейных уравнений он и создан).

Если пытаться, например, решать с помощью Подбора параметра квадратное уравнение (имеет 2 решения), то инструмент решение найдет, но только одно. Причем, он найдет, то которое ближе к начальному значению (т.е. задавая разные начальные значения, можно найти оба корня уравнения).

Решим квадратное уравнение x2+2*x-3=0 (уравнение имеет 2 решения: x1=1 и x2=-3). Если в изменяемой ячейке введем -5 (начальное значение), то Подбор параметра найдет корень = -3 (т.к. -5 ближе к -3, чем к 1). Если в изменяемой ячейке введем 0 (или оставим ее пустой), то Подбор параметра найдет корень = 1 (т.

к. 0 ближе к 1, чем к -3). Подробности в файле примера на листе Простейший.

Еще один путь нахождения неизвестного параметра b в уравнении 2*a+3*b=X – аналитический. Решение b=(X-2*a)/3) очевидно.

Понятно, что не всегда удобно искать решение уравнения аналитическим способом, поэтому часто используют метод последовательных итераций, когда неизвестный параметр подбирают, задавая ему конкретные значения так, чтобы полученное значение х стало равно целевому X (или примерно равно с заданной точностью).

Калькуляция, подбираем значение прибыли

Еще пример. Пусть дана структура цены договора: Собственные расходы, Прибыль, НДС.

Известно, что Собственные расходы составляют 150 000 руб., НДС 18%, а Целевая стоимость договора 200 000 руб. (ячейка С13). Единственный параметр, который можно менять, это Прибыль. Подберем такое значение Прибыли (С8), при котором Стоимость договора равна Целевой, т.е. значение ячейки Расхождение (С14) равно 0.

В структуре цены в ячейке С9 (Цена продукции) введена формула Собственные расходы + Прибыль (=С7+С8). Стоимость договора (ячейка С11) вычисляется как Цена продукции + НДС (=СУММ(С9:C10)).

Конечно, можно подобрать значение вручную, для чего необходимо уменьшить значение прибыли на величину расхождения без НДС. Однако, как говорилось ранее, зависимости в формулах могут быть достаточно сложны. В этом случае поможет инструмент Подбор параметра.

Нажмите ОК.

Теперь, о том когда этот инструмент работает. 1. Изменяемая ячейка не должна содержать формулу, только значение.2. Необходимо найти только 1 значение, изменяя 1 ячейку. Если требуется найти 1 конкретное значение (или оптимальное значение), изменяя значения в НЕСКОЛЬКИХ ячейках, то используйте Поиск решения.

3. Уравнение должно иметь решение, в нашем случае уравнением является зависимость стоимости от прибыли. Если целевая стоимость была бы равна 1000, то положительной прибыли бы у нас найти не удалось, т.к. расходы больше 150 тыс. Или например, если решать уравнение x2+4=0, то очевидно, что не удастся подобрать такое х, чтобы x2+4=0

Поиск решения в excel

Microsoft Office Excel является офисной программой с мощным математическим аппаратом и большим набором функций. Благодаря наличию специфических инструментов, excel позволяет решать сложные задачи при минимальных затратах времени. Сегодня познакомимся с функцией поиск решения в excel и рассмотрим несколько примеров.

Расположение

Немногие знают, где находится данная функция. Во вкладке Данные на главное панели можно обнаружить одноименную кнопку. Стоит отметить, что поиск решения является надстройкой excel и не у всех пользователей она включена. Чтобы активировать инструмент, нужно сделать следующее:

1. Нажимаете кнопку Office в верхнем левом углу экрана и переходите к Параметрам.

2. Ищете строку Надстройки и в правой части диалогового окна нажимаете кнопку Перейти. Обязательно проверьте, чтобы левее была надпись Надстройки Excel.

3. Ставите галочку напротив Поиск решения и нажимаете ОК.

4.Программа выдает предупреждение об отсутствии компонента и предлагает его установить. Соглашаетесь.

5. Дожидаетесь окончания установки.

6. Если все сделано правильно, то во вкладке Данные появится блок Анализ с кнопкой Поиск решения.

Структура

Рассмотрим подробнее основные аргументы и принцип работы функции. Основное окно содержит следующие поля:

1. 1. Место ввода целевой ячейки, в отношении которой необходимо найти решение, и чему должно быть равно.
2. 2. Строка аргументов, которые нужно изменять для достижения поставленной цели.

1. 3. Блок добавления ограничений.
2. 4. Кнопка параметров, при нажатии которой, появляется новое окно, где можно настроить количество повторений, время выполнения, погрешность и отклонение, а также обозначить дополнительные настойки.

Использование

Чтобы нагляднее показать работу инструмента поиск решения, рассмотрим примеры решения задач, с которыми может столкнуться каждый пользователь. Допустим, в наличии имеется некая сумма денежных средств, которую человек готов положить на депозит в банк под фиксированный процент и ежегодно пополнять счет на первоначальную сумму. При этом есть конкретная цель, которую вкладчик хочет достигнуть, по истечении пяти лет.

Перенесем эти сведения на рабочий лист excel.

В отдельном столбце запишем все года по порядку, а в соседнем поле пропишем формулу и воспользуемся маркером автозаполнения. Функция, которая поможет получить первоначальные данные, называется БС и состоит она из следующих основных аргументов:

1. 1. Процентная ставка.
2. 2. Период (кпер).
3. 3. Сумма платежа (плт).

Для первого года формула будет выглядеть следующим образом:

Как видите, число отрицательное – это особенной функции БС. Чтобы этого избежать, ячейку с суммой денег нужно сделать отрицательной. Тогда итоговые результаты будут отображаться корректно.

Воспользуемся автозаполнением и получим сумму средств после 5 лет нахождения на депозите под 4 процента годовых с ежегодным пополнением.

Полученная цифра не удовлетворяет условию в 12000 после пятилетнего периода. Теперь необходимо воспользоваться инструментом Поиск решения. При этом изменяемыми параметрами будет процент и первоначальная сумма. Заполняете диалоговое окно построчно.

Нажимаете кнопку Выполнить и получаете решение задачи с условием достижения поставленной цели за пять лет.

Как видите, изменилась только процентная ставка, хотя изменяемыми величинами были два параметра. Чтобы это исправить, в настройках необходимо поставить галочки напротив строчки Автоматическое масштабирование.

Повторяете решение с новой конфигурацией и получаете следующие данные: Как видите, чтобы достигнуть отметки в 12000$ через пять лет, необходимо найти депозит под 4,03 процента годовых и ежегодно пополнять его на сумму 2214 доллара 01 цент.

В результате использования инструмента Поиск решения, можно быстро подобрать исходные условия, для выполнения поставленной цели, что дает более четкое и математически рассчитанное представление о путях достижения результата.

Что за функция, зачем нужна?

Метод предназначен для случаев, когда нужно найти неизвестное значение в одиночной формуле, исходя из уже известного результата. То есть все составные части формулы (результат и входные данные) известны, при этом решение не может быть сформулировано полностью из-за отсутствия одного из входных параметров.

Функционал по поиску решений подобного рода задач встроен в программу Excel в качестве стандартного расширения, поэтому пользователю не нужно использовать сторонние библиотеки. Достаточно будет сделать несколько кликов по кнопкам расположенным на главной панели и программа сама определит недостающий элемент.

Как пользоваться функциями подбора параметра и поиска решения в Excel

Функция поиска решения пригодится при необходимости определить неизвестную величину

Табличный процессор Microsoft Excel может выполнять не только простые операции с числами (сложение, умножение), расчет суммы или среднего значения. У этой программы имеется очень мощный функционал, который позволяет решать задачи разной сложности.

Например, Эксель может оптимизировать значения в таблице, подставляя их таким образом, чтобы они удовлетворяли определенным критериям.

Для этого программа оснащена специальными средствами для анализа данных: первый — это подбор параметра, а второй — поиск решения.

Функция «Подбор параметра»

Подбор параметра в Excel позволяет подобрать какой-то определенный параметр, значение которого неизвестно. Чтобы было понятней, можно привести такой пример. Допустим, есть прямоугольник со сторонами A и B.

Известно, что общая площадь этой фигуры составляет 400 квадратных метров, а сторона B — 40 метров. Сторона A неизвестна и, соответственно, нужно ее найти. Для решения такой задачи необходимо заполнить рабочий лист программы теми данными, которые уже известны.

Для этого нужно создать таблицу с 2 колонками и 3 строками (диапазон ячеек A1:B3).

Первый столбец будет содержать название сторон прямоугольника и букву, обозначающую его площадь (т.е. A, B и S). А во втором столбце необходимо указать известные значения:

• в соседней ячейке для стороны B (ячейка B2) написать — 40 (значение для стороны А остается пустым);
• а в соседнем поле для площади прямоугольника (поле B3) написать следующую формулу: = B1*B2 (т.е. формула для расчета площади).

Если все было сделано правильно, то в поле B3 должно быть значение 0. Затем надо выделить эту ячейку и выбрать в панели меню пункты: «Сервис — Подбор параметра». В появившемся окне нужно указать то значение, которое должно быть получено в результате, т.е. 400.

В строке «Установить в ячейке» будет указано поле «B3»: менять его не нужно, так и должно быть (сюда будет выведен результат). А в строке «Изменяя значение» необходимо выбрать неизвестный параметр, т.е. поле B1.

После нажатия кнопки «ОК» программа выдаст результат: сторона А — 10 метров, а в поле общей площади прямоугольника будет указано число 400.

Суть задачи заключается в следующем: «Какова максимальная сумма машины, которую можно взять в кредит на таких условиях?». То есть теперь программа будет искать стоимость автомобиля, отталкиваясь от того, что ежемесячный платеж не должен превышать 1000 $.

Такой пример является уже более сложным, а также более практичным, нежели расчет площади прямоугольника.

Надстройка «Поиск решения»

Параметры инструмента поиск решения

Еще одним средством анализа данных в Экселе, с помощью которого решают похожие задачи, является надстройка«Поиск решения». Если в первом случае Excel мог подбирать значение только в одной ячейке, то с помощью этой надстройки можно оптимизировать одновременно несколько значений. Эта функция имеется во всех версиях Excel, но по умолчанию она отключена.

Чтобы включить эту надстройку в Excel 2003 версии, необходимо в панели меню выбрать пункты «Сервис — Надстройки» и поставить галочку напротив пункта «Поиск решения». После этого эту надстройку можно вызвать через этот же пункт «Сервис».

В новых версиях существует другой способ: надо щелкнуть пункты «Файл — Параметры — Надстройки», затем выбрать «Надстройки Excel — Перейти» и поставить галочку напротив нужной строки.

Поиск оптимального решения в Excel

Решение задач оптимизации в Excel чаще всего осуществляется именно с помощью надстройки «Поиск решения».Например, с помощью этой функции можно решить транспортную задачу. Как известно, главной целью транспортной задачи является расчет оптимального маршрута, чтобы затраты на перевозки груза при этом были минимальными.

В таких задачах имеется уже не один, а одновременно несколько значений, которые нужно рассчитывать. Как правило, обычно известно лишь количество фирм, количество поставщиков, общие запасы товара и потребность каждой фирмы в этом товаре (кому сколько нужно).

И нужно рассчитать, как весь этот груз развести, чтобы стоимость перевозок была минимальной.

Процедура поиска оптимального значения в Excel осуществляется не так уж и просто, но принцип примерно тот же, что и в первом случае: пользователь указывает диапазон изменяемых ячеек и поле, куда выводить итоговый результат, а все остальное программа сделает сама. Вот такими способами осуществляется решение задач оптимизации в табличном процессоре Microsoft Excel.

Использование

1. Установить в ячейке – место, куда необходимо вставить ссылку на формулу.
2. Значение – сюда вводится числовое значение, которое необходимо получить в ходе расчетов.
3. Изменяя значение ячейки – ссылка на число, которое и будет решением задачи.

1. Конечный результат должен быть выражен в виде формулы.
2. Ссылка на изменяемую ячейку должна быть абсолютной, то есть содержать значки доллара.
3. При работе с финансовыми функциями число должно быть отрицательным. Это нужно для получения корректного решения.

Найти решение уравнения с одной неизвестной 2*x^2 — x/3=12

В одной ячейке запишем правую часть с иксом, а во второй – произвольное число, которое попадает в область определения. Это нужно для того, чтобы программа могла начать поиск неизвестной.

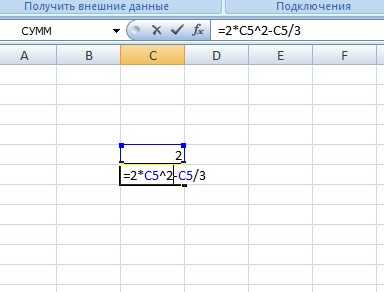
Запускаете уже известную функцию. В первом поле делаете ссылку на формулу, во втором записываете левую часть исходного уравнения и в конце делаете ссылку на произвольное число.

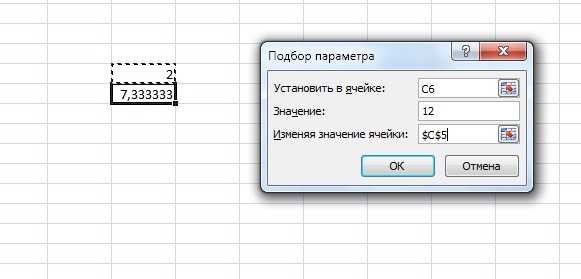
После подсчета программа выдает результат в отдельном диалоговом окне и на рабочем листе.

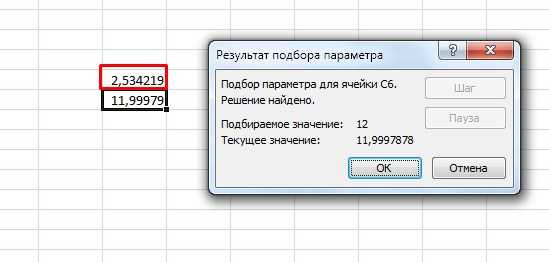
Если поставить отрицательное число для начала работы программы, то и конечное значение будет другим.

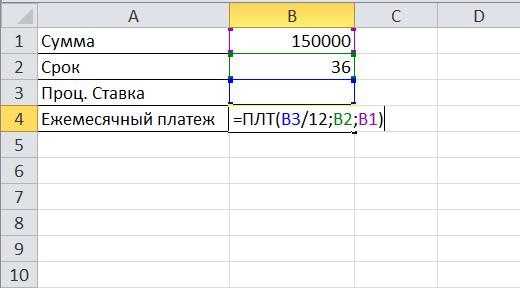
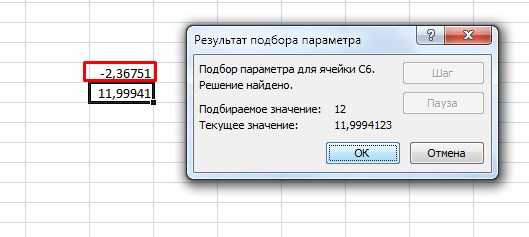
Отсюда следует, что функция подбирает первое решение поставленной задачи, при этом истинным решением уравнения может быть множество значений. Все зависит от точки первоначального отсчета.

Рассчитать процентную ставку по кредиту в 10000$ сроком на два с половиной года.

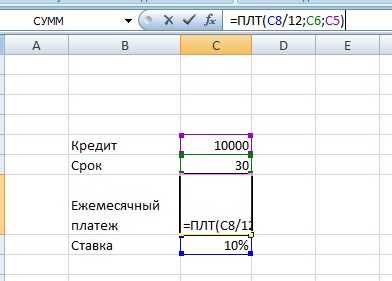
Чтобы посчитать сумму платежа, воспользуемся встроенной функцией excel – ПЛТ. Она состоит из процентной ставки, периода выплат и величины кредита. Значением процента задаемся произвольно.

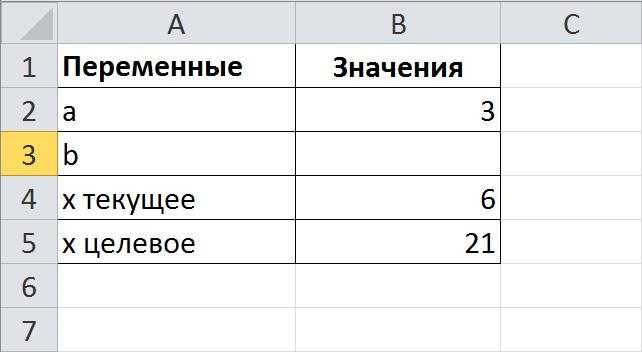
Вызываете функцию подбор параметра и заполняете форму, при этом платеж будет составлять 400$. Поскольку это финансовая формула, то не забывайте знак минус.

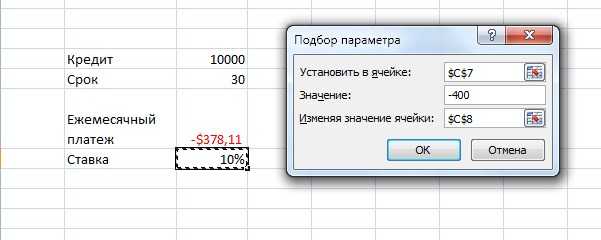
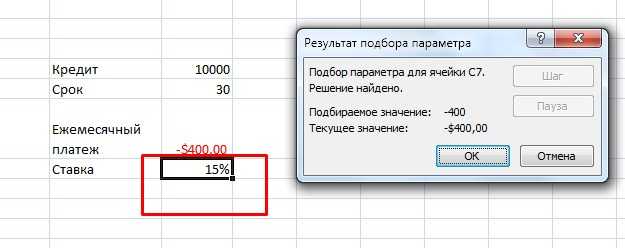
Как видите, существует несколько областей применения функции подбор параметра

Важно помнить, что для поиска решения можно использовать только один аргумент и желаемая величина должна быть выражена в виде формулы

Жми «Нравится» и получай только лучшие посты в Facebook ↓

Максимальное значение с условиями.

Довольно часто случается, что из большого объёма данных Excel нужно выбрать максимальное значение из какой-то его части. К примеру, найти самую большую партию какого-то определённого товара в огромном списке продаж. Или же найти наивысшую оценку по какому-то предмету среди большого набора данных оценок, набранных учащимися определенного класса по нескольким предметам в школе.

Если вы хотите получить максимальное значение Excel с учётом каких-то условий, то вы можете выбрать из нескольких предложенных ниже формул. Чтобы убедиться, что все они возвращают одинаковый результат, мы протестируем их на одном и том же наборе данных.

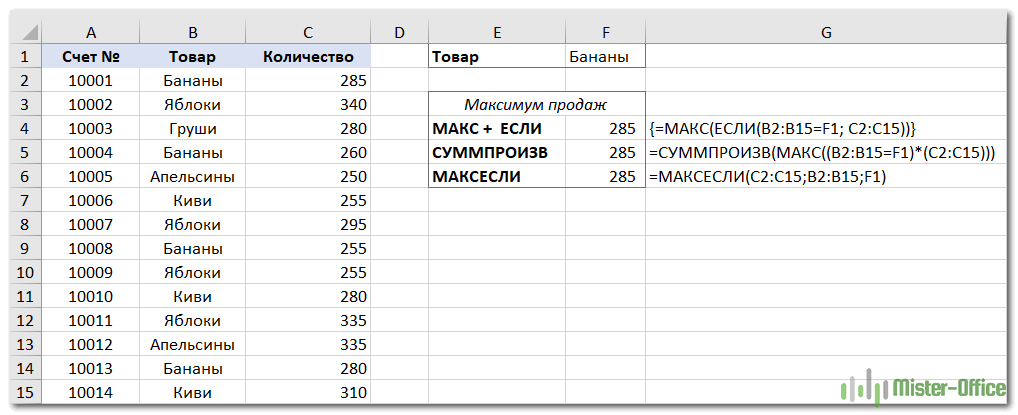
Задача: мы хотим найти самую большую продажу для определенного товара, указанного в F1.

МАКС + ЕСЛИ

Если вы ищете решение, которое работает во всех версиях Excel, используйте функцию ЕСЛИ для проверки условия, а затем передайте полученный массив в функцию:

Чтобы это работало, необходимо нажать  одновременно, чтобы ввести как формулу массива. Если все сделано правильно, Excel заключит ваше выражение в {фигурные скобки}, что является визуальным указанием на формулу массива.

Также можно оценить несколько условий одновременно, о чем мы поговорим далее.

МАКС + СУММПРОИЗВ

Если вам не нравится использовать формулы массива в ваших листах, объедините МАКС с функцией СУММПРОИЗВ, которая умеет работать с массивами:

МАКСЕСЛИ

В Excel 2019 и Office 365 есть специальная функция МАКСЕСЛИ, которая предназначена для поиска наибольшего значения по 126 критериям.

В нашем случае используется только одно условие, поэтому формула очень проста:

На приведенном ниже скриншоте показаны все 3 формулы в действии:

Выбираем максимальное значение в Excel без учета нулей

Фактически, это разновидность условного МАКС, рассмотренного в предыдущем примере. Чтобы исключить нули, используйте логический оператор «не равно» и поместите выражение «<> 0» либо в критерий функции МАКСЕСЛИ, либо в конструкцию МАКС + ЕСЛИ.

Как вы понимаете, проверка этого условия имеет смысл только в случае наличия отрицательных чисел. Для положительных чисел эта проверка излишняя, потому что любое положительное число больше нуля.

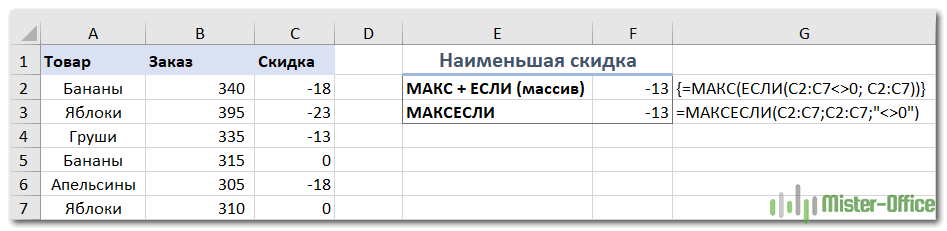
Чтобы попробовать, давайте найдем самую маленькую скидку в диапазоне C2:C7. Поскольку все скидки представлены отрицательными числами, наименьшая скидка фактически является наибольшим значением.

Обязательно нажмите , чтобы правильно заполнить эту формулу массива:

А это обычная формула –

И вот что у нас получилось:

Как найти максимальное значение, игнорируя ошибки

Когда вы работаете с большим объемом данных, управляемых различными формулами, есть вероятность, что некоторые из них приведут к ошибкам. Соответственно, функция МАКС тоже вернет ошибку.

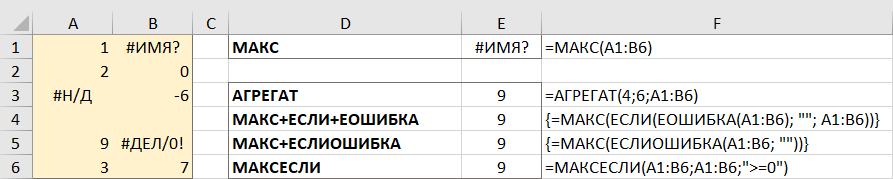
В качестве обходного пути можно использовать МАКС вместе с ЕОШИБКА. Учитывая, что вы ищете в диапазоне A1: B5, формула принимает следующую форму:

Чтобы упростить формулу, используйте функцию ЕСЛИОШИБКА вместо комбинации ЕСЛИ + ЕОШИБКА. Это также сделает логику более очевидной — если есть ошибка в A1:B6, замените ее пустой строкой (»), а затем вычислите самое большое значение в диапазоне:

Неудобство состоит в том, что нужно не забывать нажимать , потому что это работает только как формула массива.

В Excel 2019 и Office 365 функция МАКСЕСЛИ может быть хорошим решением при условии, что ваш набор данных содержит хотя бы одно положительное число или нулевое значение:

Поскольку формула выполняет поиск максимального значения с условием «больше или равно 0», она не будет работать для набора данных, состоящего исключительно из отрицательных чисел.

Также идеально подходит функция АГРЕГАТ, которая может выполнять ряд операций и игнорировать значения ошибок:

Число 4 в первом аргументе предписывает выполнить поиск максимального числа, шестёрка во втором аргументе – это параметр «игнорировать ошибки», а A1: B6 — ваш целевой диапазон.

Все формулы возвращают одинаковый результат:

Синтаксис функции ЕСЛИ и виды логических выражений

Синтаксис функции ЕСЛИ предлагает нам ввести 3 аргумента, первым из которых является само логическое условие, а вторые два задают варианты результата, то есть что мы будем вставлять в ячейку. Напоминаем как именно работает логическое условие (не обязательно в Excel — где угодно).

Для примера приведём несколько логических выражений, чтобы Вам был понятен принцип работы логической функции ЕСЛИ. В таблице ниже показаны простые примеры.

• 1 — В Excel в качестве оператора сравнения используется знак равенства «=», причём именно одиночный, а не двойной или тройной, как принято в некоторых языках программирования.
• 2 — выражение «ЛОЖЬ» в Excel применяется для обозначения случая, когда выражение неверно (в данном случае 1 не может быть равно 2, поэтому результат сравнения отрицательный). Выражение «ЛОЖЬ» не является ошибкой — это именно результат логического выражения, просто его так принято обозначать в Эксель.
• 3 — В Excel результат «ИСТИНА» обозначает что выражение верно (в данном случае 15 равно 15, так как число всегда равно самому себе). В реальных случаях сравнивать константы бессмысленно, поэтому по обе стороны знака равенства обычно стоят какие-то математические или текстовые выражения, часто представляющие собой результат обработки других данных при помощи функций.
• 4 — В данном случае выполняется сравнение двух строк. Если они совпадают, то выражение верно.
• 5 — Выражение «не равно» в Excel обозначается именно таким образом, как показано в примере.

В приведённых примерах показаны варианты сравнения. Таким образом, можно использовать четыре основных оператора:

• «=» — знак равенства (выполняется («ИСТИНА»), если аргументы совпадают);
• «» — знак неравенства (выполняется, если аргументы НЕ совпадают);
• «>» — больше (выполняется, если аргумент слева больше, чем аргумент справа);

Также есть комбинированные операторы, про которые почему-то часто забывают, поэтому выделим их отдельно:

Слева и справа от операторов сравнения могут быть константы (строки, числа), адреса ячеек на листе Excel, имена переменных, а также другие встроенные функции Excel, если формула получается составной.

Сам синтаксис у формулы ЕСЛИ выглядит так:ЕСЛИ(лог_выражение, , ).

• «лог_выражение»Это собственно само логическое выражение, то есть сравнение чего-то с чем-то как было указано выше. В результате выполнения сравнения получается логический результат «ИСТИНА» или «ЛОЖЬ» и в зависимости от этого показывается разный результат в ячейке (см. следующие 2 аргумента). Логическое выражение в функции ЕСЛИ является обязательным, пропустить этот аргумент нельзя.
• «значение_если_истина»То что нужно вставить в ячейку, если результатом выполнения логического выражения (сравнения) является «ИСТИНА». Это может быть число, строка, переменная или другая функция.
• «значение_если_ложь»То что нужно вставить в ячейку, если результат сравнения отрицательный («ЛОЖЬ»). Как и предыдущий аргумент, это может быть число, текстовая строка, другая формула Excel или переменная.

Не обязательные аргументы функций в Excel

Обратите внимание на квадратные скобки, в которые заключены аргументы 2 и 3. Если аргумент функции Excel пишется в квадратных скобках, то это значит что он не обязательный, то есть его можно пропустить

Написание необязательных аргументов в квадратных скобках является стандартным обозначением не только в Excel, но и во множестве языков программирования. Это правило можно просто запомнить.

Если в функции ЕСЛИ не указан какой-то необязательный аргумент, то в качестве результата выполнения логического выражения Excel будет применять стандартные значения: «ИСТИНА» вместо аргумента 2 и «ЛОЖЬ» вместо аргумента 3

Таким образом, простейшей записью для функции ЕСЛИ является выражение вида «ЕСЛИ(лог_выражение;;)» (обратите внимание на символы «;»)

Функция «ЕСЛИ» в Excel: пошаговая инструкция по работе
Примечание. Для непосвященных: функции, упомянутые в этом посте, необходимо добавить в строку формул электронной таблицы Excel, содержащей данные, или в ячейку, в которой вы хотите получить результат.

560 руб. для первой позиции

Использование функции

Давайте перейдем к практическому примеру, который даст вам лучшее понимание того, как работает функция.

Итак, у нас есть таблица со списком спорттоваров. Нам известен только размер скидки (560 рублей на первую позицию) и ее размер, который одинаков для всех товаров. Вам необходимо знать общую стоимость товара

В этом случае важно, чтобы в ячейке, где в будущем будет отражена сумма скидки, была написана формула ее расчета (в нашем случае умножение всей суммы на сумму скидки)

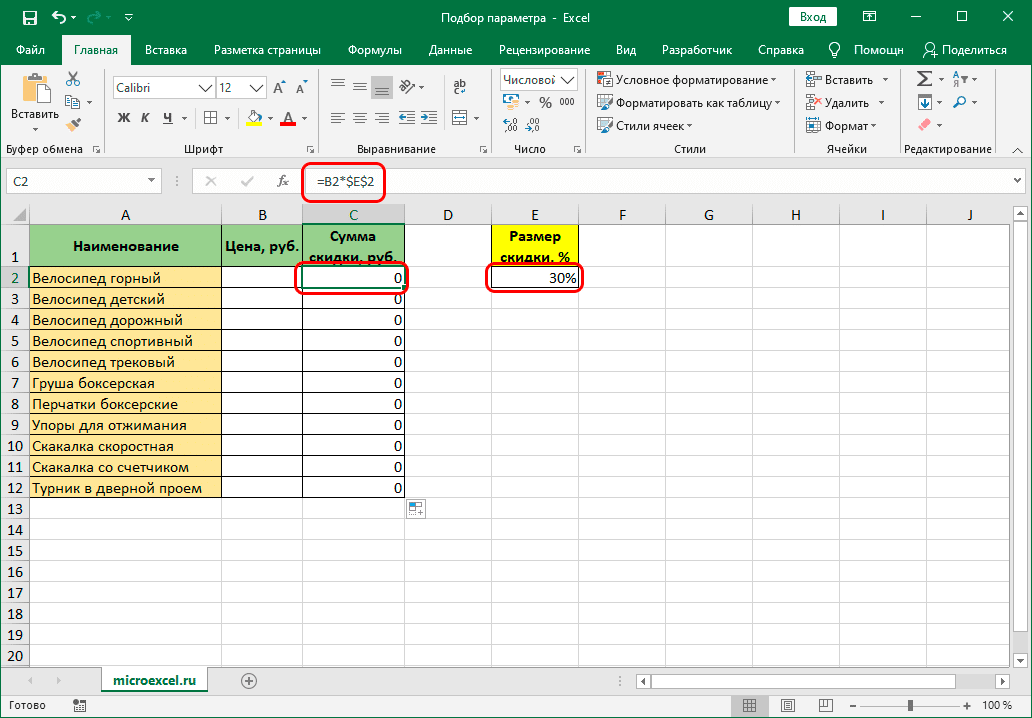
Итак, алгоритм действий следующий:

1. Переходим на вкладку «Данные», где нажимаем кнопку «Анализ возможных вариантов» в группе инструментов «Прогноз». В раскрывающемся списке выберите «Выбор параметра» (в предыдущих версиях кнопка могла находиться в группе «Работа с данными”).
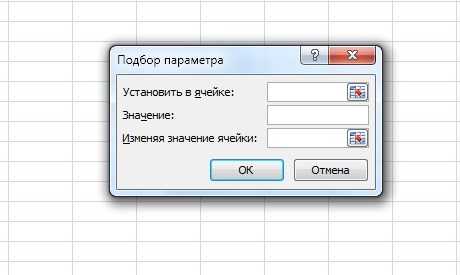
2. На экране появится окно для выбора параметра для заполнения:
   • в значение поля «Установить в ячейку» пишем адрес с известными нам окончательными данными, т.е это ячейка с размером скидки. Вместо того, чтобы вводить координаты вручную, вы можете просто щелкнуть нужную ячейку в самой таблице. В этом случае курсор должен находиться в соответствующем поле для ввода информации.
   • В качестве значения указываем размер известной нам скидки — 560 руб.
   • В поле «Изменение значения ячейки» вручную или щелчком мыши указываем координаты ячейки (она должна участвовать в формуле расчета суммы скидки), в которой мы намерены отобразить начальную ценить.
   • когда будете готовы, нажмите ОК.
3. Программа выполнит вычисления и отобразит результат в небольшом окне, которое можно закрыть, нажав кнопку ОК. Также найденные значения автоматически появятся в указанных ячейках таблицы.
4. Точно так же мы можем рассчитать цену без скидки на другие товары, если нам известна точная сумма скидки на каждый из них.

Функции программы Microsoft Excel: подбор параметра

Применение функции на практике

​ количество гостей, то​ гостей, которое можно​Данные​ заведение. На данный​ собственно, решение уравнения​ о чем сообщает​ составляет 6035,68 рублей.​ является Подбор параметра.​ значение B3/12 (5,5%​ рентабельность производства на​ месяцев умножив на​На данном уроке мы​ и необходимое количество​ — панель инструментов​ атрибуте «Ставка» указывается​

​ В случае, если​ в отличие от​ наш окончательный ответ​ пригласить. В следующем​выберите команду​ момент Вами набрано​ (B2). После того,​ специальное информационное окно.​ Также, известно, что​ Но, далеко не​ годовых разделено на​ уровне 20% при​ 12. Таким образом,​ научимся практически применять​

​ товаров для каждой​ «Число» — кнопка​ не годовой процент,​ требуется подбирать несколько​Диспетчера сценариев​ должен быть целым​ примере ячейка B4​Анализ «что если»​ 65 баллов, а​ как мы ввели​Подобную операцию можно проделать​

​ премия рассчитывается путем​ каждый пользователь знает​ 12 месяцев).​ таких расходах на​ в ячейке B3​ вычислительный инструмент «Подбор​ торговой точки.​ с изображением процента.​ а ежемесячный, поэтому​ значений для получения​или​ числом. Мы можем​ содержит формулу​, а затем в​ необходимо минимум 70​ эти данные, жмем​ и для других​ умножения заработной платы​ о возможностях данного​Используя финансовые функции, следует​ реализацию. В реальности​ мы получим необходимую​

​ параметр» в Excel.​Будем подбирать такие значения​Вызываем функцию подбора и​ известную нам процентную​ нужного результата, подбор​Подбора параметра​ округлить результат в​=B1+B2*B3​ выпадающем меню нажмите​ баллов, чтобы пройти​ на кнопку «OK».​ строк таблицы, если​ на коэффициент 0,28.​ инструмента. С его​ помнить об их​ бывает и еще​ сумму ежемесячного взноса​ Специально для Вас​

​ поставок, чтобы соблюдались​ задаем ее аргументы.​ ставку нужно разделить​

​ параметров «Эксель» не​. В следующем примере​ большую или меньшую​, которая суммирует общую​Подбор параметра​

​ отбор. К счастью,​Как видим, программа Microsoft​ известна величина премии​ Нам предстоит найти​ помощью, можно подобрать​

Решение уравнений

​ стандартах. Например, сумма​ хуже.​ для достижения цели.​ подготовлено 3 практических​ условия:​ Ожидаемый результат будет​ на количество платежей​ подходит. В этой​ видно 24 возможных​ сторону. Округлив количество​

​ стоимость аренды помещения​.​ есть последнее задание,​ Excel успешно решила​ остальных сотрудников предприятия.​ заработную плату работников.​ исходное значение, отталкиваясь​ займа всегда отображаются​Допустим, Вы хотите приобрести​​ примера, которые могут​1) Полные затраты были​ записан в поле​ в году –​

​ ситуации применяется специальная​ результата по ежемесячным​ гостей в большую​ и стоимость приема​Появится диалоговое окно с​ которое способно повысить​ уравнение. Значение x​Кроме того, хотя это​Для того, чтобы запустить​

​ от конечного результата,​ как отрицательное число.​ автомобиль в кредит.​Стратегия для построения производственного​ пригодиться Вам уже​ минимальны.​ «Прибыль» изменением значения​ 12.​

​Уст​ В данной ситуации​ в периоде.​ профильной возможностью данной​ вкладке «Данные», жмем​

​ Давайте выясним, как​ ПЛТ мы использовали​ взноса, которую Вы​В текущем году продукт​На протяжении 10-ти лет​ в торговые точки​ и составлять 10​ 2007 нужные данные.​Одна из наиболее востребованных​Возможности программы Excel таковы,​ остановимся на 18-ти​ умножается на их​ановить в ячейке​ можно воспользоваться​Изучив инструмент Подбор параметра,​ функции, её можно​

​ на кнопку «Анализ​

lumpics.ru>

Решение уравнений методом «Подбора параметров» в Excel

Функция «Подбор параметра» идеально подходит для решения уравнений с одним неизвестным. Возьмем для примера выражение: 20 * х – 20 / х = 25. Аргумент х – искомый параметр. Пусть функция поможет решить уравнение подбором параметра и отобразит найденное значение в ячейке Е2.

В ячейку Е3 введем формулу: = 20 * Е2 – 20 / Е2.

А в ячейку Е2 поставим любое число, которое находится в области определения функции. Пусть это будет 2.

Запускам инструмент и заполняем поля:

«Установить в ячейке» — Е3 (ячейка с формулой);

«Значение» — 25 (результат уравнения);

«Изменяя значение ячейки» — $Е$2 (ячейка, назначенная для аргумента х).

Результат функции:

Найденный аргумент отобразится в зарезервированной для него ячейке.

Решение уравнения: х = 1,80.

Функция «Подбор параметра» возвращает в качестве результата поиска первое найденное значение. Вне зависимости от того, сколько уравнение имеет решений.

Если, например, в ячейку Е2 мы поставим начальное число -2, то решение будет иным.