Прямоугольник. онлайн калькулятор

Информация о прямоугольнике

Прямоугольник — четырехугольная геометрическая фигура, противолежащие стороны которой равны и углы являются прямыми. Частным случаем данной фигуры считается квадрат. У него все углы прямые, а также все стороны равны между собой. Для выполнения расчетов нужно знать основные соотношения, свойства и признаки.

Важным аспектом является идентификация фигуры и применение к ней формул и соотношений. В двухмерной геометрии, которую еще называют эвклидовой, можно встретить необычный признак, позволяющий определить принадлежность четырехугольника к прямоугольнику. Его формулировка следующая: достаточно хотя бы трех углов, равных 90 градусам, чтобы четырехугольник считался прямоугольником.

Утверждение легко доказывается. Это связано с тем, что по теореме о сумме внутренних углов произвольного четырехугольника, составляющей 360 градусов, четвертый угол тоже равен 90. Нужно выполнить следующие расчеты для определения градусной меры четвертого угла: D = 360 — (90 + 90 + 90) = 90. Необходимо отметить, что смежные с ними углы равны 90.

Свойства и признаки

Очень часто новички путают свойства и признаки фигуры. Однако это совсем различные понятия. Признаками фигуры называются характерные особенности, которые позволяют отнести ее к тому или иному классу. Свойства — совокупность аксиом, позволяющих использовать некоторые данные при решении или доказательстве теорем и тождеств. Прямоугольник обладает следующими признаками:

1. Условие параллельности и равенства противоположных сторон.
2. Наличие четырех прямых углов.
3. Равенство диагоналей.
4. Квадрат диагонали равен суммарному значению квадратов двух сторон, которые не противоположны.
5. Все стороны не равны между собой.

Очень важно уметь различать геометрические фигуры. Поскольку прямоугольник является параллелограммом, то их часто путают

Основное его отличие — это равенство всех углов 90 градусов. У параллелограмма и ромба углы будут равняться 90 в том случае, когда они являются квадратами. Последний отличается от искомой фигуры (прямоугольника) равенством всех сторон. Поскольку прямоугольник является частным случаем параллелограмма, то обладает такими же свойствами:

1. Углы равны между собой 90 градусов.
2. Противолежащие параллельные стороны равны.
3. Сумма всех внутренних углов составляет 360.
4. Диагональ, проведенная внутри прямоугольника, делит его на два равнозначных треугольника, которые являются равновеликими. Они равны по третьему признаку равенства треугольников (размерности сторон одной фигуры равны значениям сторон другой фигуры).
5. Треугольники, полученные при проведении двух диагоналей, равны по всем признакам (углам и сторонам).
6. Диагонали пересекаются между собой в точке, которая делит их на четыре равные части.
7. Точка пересечения диагоналей — центр симметрии.
8. Сумма квадратов двух диагоналей соответствует суммарному значению квадратов всех сторон фигуры.

https://youtube.com/watch?v=4vTTG8M_mvU

Периметр и размерность

Нужно ввести некоторые обозначения. Пусть стороны прямоугольника АВСД обозначаются литерами a и b. Поскольку диагонали равны, то можно только обозначить размерность одной буквой «d». Периметром называется сумма всех сторон заданной фигуры. Он обозначается литерой P. Для его нахождения применяется формула такого вида: P = 2 * (a + b). Однако бывает случай, когда известна только одна его сторона и диагональ. Формула приобретает следующий вид: P = 2a + ^(1/2) и P = 2b + ^(1/2).

Чтобы вычислить площадь прямоугольника, следует воспользоваться таким соотношением: S = a * b. Эта базовая формула, которая используется также в строительной сфере и физике. Однако существует еще один способ, с помощью которого можно узнать площадь прямоугольника. Она находится с помощью формулы Герона для треугольников с площадями S1 и S2, а затем результат умножается на 2. Эта особенность основывается на свойстве фигуры, поскольку диагональ делит его на два равных треугольника.

Соотношение имеет следующий вид: S = S1 + S2 = 2S1= 2 * ^(1/2). Переменная «p» — полупериметр треугольника. Он находится таким методом: p = P / 2 = (a + b + d) / 2.

Как найти сторону треугольника, если известна его площадь?

Вычисление сторон треугольника может быть достаточно сложным, но подсчет его площади с помощью простых формул является обычным делом. Кроме того, если имеется площадь треугольника и некоторые другие параметры, например, его высота, то можно легко найти его сторону.

Формула для вычисления площади треугольника: S = (b * h) / 2, где S — площадь треугольника, b — основание, h — высота.

Формула для вычисления основания треугольника: b = (2S) / h, где S — площадь треугольника, h — высота.

Если известна площадь треугольника и его высота, то можно определить его основание. Однако для того чтобы найти все стороны треугольника, вам понадобится иметь дополнительные измерения, например, углы или другие стороны.

Если вы знаете все три стороны треугольника, то можно использовать формулу Герона для вычисления его площади и далее применять формулы для вычисления сторон треугольника:

• Формула для вычисления полупериметра треугольника: p = (a + b + c) / 2, где a, b, c — стороны треугольника.
• Формула для вычисления площади треугольника по формуле Герона: S = √p(p — a)(p — b)(p — c), где S — площадь треугольника, p — полупериметр, a, b, c — стороны треугольника.
• Формула для вычисления стороны треугольника: a = 2S / (bc), где a — сторона, b, c — другие стороны, S — площадь треугольника.

Помните, что вычисления могут быть неточными, если измерения неправильно взяты, поэтому следует убедиться, что измерения правильные и точные перед использованием указанных формул.

Как вычислить площадь прямоугольника с разными сторонами

Согласно данной документации, на каждые 8 «квадратов» поверхности пола приходиться должно не менее одного «квадрата» источника естественного светового потока. На мансардных этажах эта пропорция не может быть менее 1:10.

Чтобы обеспечить качественное проведение ремонта нужно заранее выяснить, как вычислить площадь пола и другие необходимые размеры помещения. Подготовительный этап также предусматривает приобретение стройматериалов и тогда в процессе ремонта затраты будут сведены к минимуму, поскольку не получится больших остатков и стоимость доставки обойдется недорого.

Ручной способ вычислений как узнать площадь пола займет больше времени, чем при проведении расчетов на уже имеющемся строительном калькуляторе, но он позволяет узнать более точные результаты.

Как рассчитывается площадь прямоугольника?

Расчет площади прямоугольника – это достаточно непростая задача, которая требует определенного времени и усилий для достижения поставленных целей. Существуют самые разные методы, которые используются для проведения расчетов. Каждый отличается определенными преимуществами и свойствами, которые необходимо учитывать. В противном случае не получится получить максимально точный и понятный результат

Важно при проведении расчетов максимально следовать всем рекомендациям, а также соблюдать формулы. Необходимо учитывать все перечисленные характеристики, что позволит достичь оптимальных результатов

Ниже приведены наиболее распространенные методологии, которые применяются при проведении операции расчетов.

Две соседние стороны

Если человек знает две соседние стороны, то он может использовать их для проведения расчетов. Для этого достаточно использовать их числовые значения. Их просто нужно перемножить для того, чтобы получить верный результат. Это не составляет никакого труда.

Например, вы можете использовать две соседние стороны – одну короче и одну длиннее для того, чтобы получить искомое число. Обычно эта операция не занимает много времени. В результате умножения получается достичь искомого результата и провести правильные расчеты.

Сторона и диагональ

Для проведения расчетов площади прямоугольника по формуле можно использовать значение диагональной линии, а также опираться на одну из сторон. Для начала нужно узнать диагональную линию прямоугольника. Также для расчетов можно использовать любую другую известную сторону. Это может быть любая сторона прямоугольной фигуры. Для достижения нужных результатов необходимо отнять от квадрата диагонали квадрат известной стороны. После этого нужно извлечь квадратный корень этих сторон.

Далее полученный результат используется для вычисления площади. Для этого необходимо одну из известных сторон умножить на полученное значение. Результат и будет искомым решением.

Сам процесс расчетов не занимает много времени, поэтому выполняется достаточно быстро при известных значениях для расчетов.

Сторона и диаметр окружности

Далее для расчета площади прямоугольника можно использовать диаметр известной окружности при любой стороне фигуры. Далее остается только отнять два известных числа, после чего извлечь квадратный корень от полученного результата. Формула выглядит так:

Остается только перемножить полученное значение с суммой квадратного корня для того, чтобы получить искомый результат площади. Обычно этот процесс не занимает много времени, поэтому проводится достаточно быстро для достижения нужного результата со стороны пользователя.

Сторона и радиус

При известной стороне прямоугольника и радиусе окружности можно использовать эти значения для того, чтобы получить квадратный корень. Полученный результат перемножают для вычисления площади. Эта задача выполняется быстро. Необходимо только знать квадратный корень и радиус описанной окружности. Также нужно правильно использовать значение искомой стороны. В примерах ниже будет рассмотрен данный вариант исчисления по формуле:

Сторона и периметр

Для получения нужного значения необходимо умножить значение периметра рассматриваемой фигуры, а также использовать для получения результата длину от известной стороны. Для этого нужно использовать периметр и известную сторону, отняв от этого значения квадрат известной стороны. Также полученное значение необходимо в обязательном порядке разделить на два для достижения требуемых результатов. Формула выглядит так:

Диагональ и угол

Для проведения расчетов могут использоваться угловые значения. Для этого нужно для начала вычислить значение диагонали. После этого нужно обязательно разделить полученное значение на два для того, чтобы отыскать нужный результат. Далее нужно получить синус известного угла, а после этого использовать значение для проведения нужных вычислений. Формула выглядит так:

Радиус и угол

Для получения нужных значений можно использовать радиус окружности, которая была описана вокруг прямоугольной фигуры. Также полученный результат можно умножить на два, а после этого отыскать синус для получения требуемого результата. Формула для расчетов выглядит так:

Нахождение площади четырёхугольника различными способами и методами

Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2).

Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных.

Теперь пусть даны стороны и противолежащие углы четырёхугольника.

Пусть a, b, c, d известные стороны многоугольника; p — его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d).

На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров.

Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996.

Подставим полученные данные в нашу формулу, получим: S = rad((40 — 18)*(40 — 23)*(40 — 22)*(40 — 17) — 18*23*22*17*0,97) = rad(22*17*18*23 — 18*23*22*17*1/4) = rad((22*17*18*23*(1 — 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного.

Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным.

Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид:

Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим:

S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных.

Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой:

S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров.

Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим:

S = rad((65 — 26)*(65 — 35)*(65 — 39)*(65 — 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных.

Определения и соглашения

В приведённой ниже таблице будут указаны определения и договорённости, которые будут использоваться в дальнейшем во время наших рассуждений.

1. Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
2. Диагональ — отрезок, соединяющий вершины многоугольника не лежащие на одной стороне (её обозначение – латинская буква d).
3. Площадь фигуры — это численное значение территории, заключённой внутри многоугольника (её обозначение – латинская буква S).
4. Синус угла — это число равное отношению противоположного катета к гипотенузе в прямоугольном треугольнике. (её обозначение – запись sin).
5. Косинус угла — это число равное отношению прилежащего катета к гипотенузе в прямоугольном треугольнике. В дальнейшем в статье для его обозначения будем использовать латинскую запись cos.
6. Описанная окружность — это окружность, которой принадлежат все вершины многоугольника ( её радиуса обозается буквой R).
7. Вписанная окружность — это окружность, которая касается всех сторон многоугольника. В дальнейшем в статье для обозначения её радиуса будем использовать латинскую букву r.
8. Угол между сторонами a и b будем обозначать следующей записью (a,b).

Единицы измерения площади

Единицы измерения площади — это площадь квадратов, у которых стороны равны либо единице измерения длины, либо 10 м, либо 100 м: 1 кв.мм (квадрат со стороной 1 мм), 1 кв.см (квадрат со стороной 1 см), 1 кв.дм (квадрат со стороной 1 дм), 1 кв.м (квадрат со стороной 1 м), 1 кв.км (квадрат со стороной 1 км), 1 ар (квадрат со сторонами 10 м), 1 га (квадрат со стороной 100 м). (<См. статью “Единицы измерения площади”>)

В каких единицах измерения площади мы можем записать площадь донышка одного ряда? — продолжил вопрос Бим.

Оля ответила сразу:

— Если мы будем укрупнять, то в дециметрах и сантиметрах.

576 кв.см = 5 кв.дм 76 кв.см

— А если мы будем раздроблять — в миллиметрах, — добавил Коля. —

576 кв.см =576 х 100 (кв.мм).

А еще единицы измерения площади 1 кв.м (квадрат со стороною 1 м), 1 кв.км (квадрат со стороной 1 км), 1 ар (квадрат со сторонами 10 м), 1 га (квадрат со стороной 100 м).

— Теперь я подпишу открытку. У меня красивый артистический почерк, — вызвался Бом.

— Хорошо, Бом. А мы с ребятами составим вопросы и ответы на них, — согласился Бим.

— Первый вопрос: Что называется площадью? — начал Вася.

— Второй вопрос: Дайте определение прямоугольника. — продолжил Коля. —

И третий вопрос: Что такое площадь прямоугольника?

— Четвертый вопрос: Как найти площадь прямоугольника (с разными сторонами)? — закончила Оля.

— И еще один, пятый, вопрос: Какие вы знаете единицы измерения площади? — добавил Бим.

Теперь я запишу ответы для проверки, — продолжил клоун:

1.      Площадь — это размер куска плоскости внутри фигуры.

2.      Прямоугольник — это фигура с 4-мя прямыми углами и с замкнутой границей из четырех отрезков.

3.      Площадь прямоугольника — это площадь куска плоскости внутри границ прямоугольника.

4.      Как найти площадь прямоугольника? Для нахождения площади прямоугольника перемножаются длины двух прилежащих сторон. Результат записывается в единицах измерения площади.

5.      Единицы измерения площади — это площади квадратов, у которых стороны равны либо единице измерения длины, либо 10 м, либо 100 м: 1 кв.мм (квадрат со стороной 1 мм), 1 кв.см (квадрат со стороной 1 см), 1 кв.дм (квадрат со стороной 1 дм), 1 кв.м (квадрат со стороной 1 м), 1 кв.км (квадрат со стороной 1 км), 1 ар (квадрат со сторонами 10 м), 1 га (квадрат со стороной 100 м).

Итог подвел Бом:

— Мы сегодня узнали :

что такое площадь

что такое площадь прямоугольника

как найти площадь прямоугольника

единицы измерения площади.

Всем спасибо за помощь.

Формулы площади

Площадь геометрической фигуры
— часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади выражается числом заключающихся в него квадратных единиц.

Формулы площади треугольника

1-ая формула

S
— площадь треугольника

a, b
— длины 2-х сторон треугольника

С
— угол между сторонами a и b

2-ая формула

S
— площадь треугольника

a
— длина стороны треугольника

h
— длина высоты, опущенной на сторону a

3-ья формула

S
— площадь треугольника

a, b, c

p
— полупериметр треугольника

4-ая формула

S
— площадь треугольника

r
— радиус вписанной окружности

p
— полупериметр треугольника

5-ая формула

S
— площадь треугольника

a, b, c
— длины 3-х сторон треугольника

R
— радиус описанной окружности

См. также: Программа для расчета площади треугольника.

Формулы площади квадрата:

1) Площадь квадрата равна квадрату длины его стороны (a).

2) Площадь квадрата равна половине квадрата длины его диагонали (d).

S
— площадь квадрата

a
— длина стороны квадрата

d
— длина диагонали квадрата

См. также: Программа для расчета площади квадрата.

Формула площади прямоугольника:

1) Площадь прямоугольника равна произведению длин двух его смежных сторон (a, b).

S
— площадь прямоугольника

a
— длина 1-ой стороны прямоугольника

b
— длина 2-ой стороны прямоугольника

См. также: Программа для расчета площади прямоугольника.

Формула площади параллелограмма:

1) Площадь параллелограмма равна произведению длины его основания на длину высоты (a, h).

S
— площадь параллелограмма

a
— длина основания

h
— длина высоты

См. также: Программа для расчета площади параллелограмма.

Формула площади трапеции:

1) Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).

S
— площадь трапеции

a
— длина 1-ого основания

b
— длина 2-ого основания

h
— длина высоты трапеции

Определения

Поговорим о нескольких определениях, которые необходимы для того, чтобы разобраться в этой теме.

Прямоугольник – это выпуклый четырехугольник, стороны которого попарно равны и параллельны, а углы равняются 90 градусам. Частным случаем прямоугольника является квадрат. Квадрат – это прямоугольник, у которого все стороны равны между собой.

Рис. 1. Прямоугольник.

Что такое диагональ? Диагональ – это отрезок, который соединяет противолежащие стороны фигуры. Диагональ существует во всех фигурах, число вершин которых больше 3.

Четырехугольники подразделяются на выпуклые и невыпуклые. Выпуклые четырех угольники определяют по следующему правилу: через любые две соседние вершины фигуры проводят прямую. Если фигура лежит по одну сторону от прямой, то четырехугольник выпуклый, если нет – невыпуклый. Все известные четырехугольники являются выпуклыми.

Рис. 2. Невыпуклый четырехугольник.

Площадь — это?

Площадь любого куска плоскости (фигуры)— это размер этого куска плоскости (куска плоскости внутри границ фигуры), измеренный в единицах измерения площади.

Бим и Бом пришли на работу в цирк пораньше. Бим зашел к Бому в гримерку.

— Привет, Бим!

— Привет, Бом!

— У нашей Буфетчицы сегодня день рождения. Я купил очень вкусных конфет, только вот упаковка видишь какая длинная. У тебя есть какая-нибудь красивая коробка, куда мы можем сложить конфеты и подарить Буфетчице?

— У меня много разных красивых коробочек. Но как мы узнаем, какая из них подходит, чтобы вместились все конфеты и было красиво?

Бом и Бим задумались.

— Ура!!! Придумал, — нашелся Бим. — У каждой коробки есть плоское донышко. Давай вычислим площади донышек у каждой коробки, то есть измерим площадь донышек в единицах измерения площади — квадратных сантиметрах.

— Тогда найдем, какая коробка подходит больше всего, — подхватил Бом. — Начнем с упаковки, где лежат конфеты. У упаковки донышко в виде прямоугольника. Значит, достаточно измерить длины короткой и длинной стороны.

— А чем будем измерять? — задумался Бим.

— Сейчас поищу, — ответил Бом. — Вот у меня есть сантиметр, линейка и листочек в клеточку.

— Дай, пожалуйста, мне листочек в клеточку, — попросил Бом. — Я проверю, что донышко упаковки — прямоугольник.

Свойства прямоугольника

Прямоугольник – это одна из базовых геометрических фигур. Вы можете легко использовать калькулятор площади прямоугольника для того, чтобы отыскать искомый результат и минимизировать для себя возможные затраты.

Прямоугольник обладает некоторыми свойствами

Среди них следует особое внимание обратить на такие:

• Противоположные стороны данной геометрической фигуры обладают одинаковыми свойствами и параметрами. Одинаковые размеры позволяют проводить вычисления намного проще и быстрее, а также минимизировать возможные затраты в процессе.
• Все диагональные линии данной фигуры обладают также одинаковыми свойствами, поэтому отличаются простотой функционирования, не доставляя особых проблем пользователям при проведении расчетов.
• Все стороны также являются и высотой, поэтому для проведения расчетов не потребуется использовать дополнительные параметры.
• Квадраты противоположных сторон являются суммой квадратов их смежных значений, поэтому по теореме Пифагора позволяют намного проще отыскать значение площади, минимизируя дополнительные затраты на это в процессе.
• Прямоугольник – это одна из фигур, которая может быть использована для того, чтобы описать вокруг нее окружность. Это свойство позволяет проводить дополнительные расчеты и получать нужные результаты в процессе расчетов.

Прямоугольник – это фигура, которая обладает многими интересными свойствами. Например, все углы у этой фигуры являются прямыми, поэтому для проведения расчетов можно использовать данное свойство, чтобы отыскать площадь, периметр и другие значения, которые могут потребоваться в процессе изучения данной геометрической фигуры. Прямоугольник обладает определенными комбинациями и свойствами, которые могут быть полезны для проведения дополнительных вычислений с другими геометрическими фигурами.

Также следует обратить внимание на некоторые вспомогательные свойства данной фигуры. Например, две стороны являются более длинными, а две другие – короткими

Площадь может исчисляться несколькими различными способами, что позволяет использовать множество разных значений для достижения определенных результатов.

Как рассчитать площадь прямоугольника

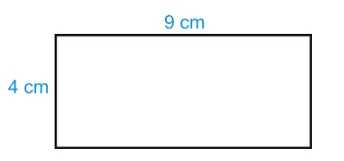
Прямоугольником принято называть геометрическую плоскую фигуру, которая имеет параллельно расположенные противоположные стороны при углах в 90 градусов. В качестве длины этой геометрической фигуры выступает величина, которая имеет большую сторону. При этом, за ширину принимается величина меньшей стороны. Для правильного вычисления площади прямоугольника Вам необходимо знать определённые параметры, которыми обладает данная фигура. В их числе:

• диагональ;
• ширина;
• так называемый угол наклона к одной из сторон диагонали;
• длина.

Таким образом, произвести расчёт площади прямоугольника можно различными способами. Всё зависит от количества информации о фигуре, а именно, какие величины нам точно известны.

Как вычислить площадь прямоугольника, имея линейные параметры его сторон?

Давайте в качестве обозначения длины прямоугольника будем использовать букву «а», для его ширины – букву «b», а площадь геометрической фигуры обозначим буквой «S». Согласно этому, наша формула будет выглядеть следующим образом: S = a x b.

Зная линейные параметры прямоугольника, можно легко определить его периметр последующей формуле: P = 2(a + b), где в качестве обозначения периметра мы используем букву «P».

Как можно вычислить площадь прямоугольника, зная величину одну из его сторон и диагональ?

Как нам известно, диагональ делит любой прямоугольник на два так называемых прямоугольных треугольника. Давайте присвоим диагонали индекс «с», а длину стороны обозначим буквой «а». Теперь необходимо произвести следующий порядок действий:

1. для начала необходимо найти длину неизвестной стороны. Для этого мы используем формулу Пифагора: b = V c2 – a2.
2. После этого, нам следует определить площадь нашей основной геометрической фигуры (прямоугольника) как площадь треугольника, умноженную на два: Sтр = ½ (а х в).
3. Согласно вышеописанной схеме расчёта площадь прямоугольника в данном случае будет равна: S = 2 x Sтр = а х в.

В том случае, если нам известны периметр прямоугольника, а также длина одной из его сторон, то площадь этой геометрической фигуры можно вычислить, определив длину второй стороны (b = (P – 2xa), по такой формуле: S = a x b.

Если же нам известны размер диагонали прямоугольника, а также угол между стороной и самой диагональю, то площадь можно вычислить при помощи следующих тригонометрических функций: Sтр = ½ х с2 х sinФ х cosФ.

При этом, общая площадь в данном случае будет составлять S = 2 x Sтр.

Вопрос-ответ:

Как вычислить площадь прямоугольника, если известна только его диагональ?

Для вычисления площади прямоугольника по его диагонали необходимо знать хотя бы одну из следующих величин: длину или ширину. Если известна только диагональ, то для расчета площади можно воспользоваться формулой: S = (d^2)/2, где S — площадь, d — диагональ. Подставляем известное значение диагонали и получаем значение площади. Однако, для точного вычисления необходимо знать значения длины и ширины.

Как найти длину прямоугольника, если известна его диагональ и ширина?

Для нахождения длины прямоугольника по известным диагонали и ширине необходимо воспользоваться теоремой Пифагора: d^2 = l^2 + w^2, где d — диагональ, l — длина, w — ширина. Известны значения диагонали и ширины, подставляем их в формулу и находим длину: l = √(d^2 — w^2).

Можно ли вычислить площадь прямоугольника, если известны только периметр и диагональ?

Нет, для вычисления площади прямоугольника необходимо знать значения длины и ширины. Из периметра можно найти только сумму двух сторон, но не их значения отдельно. Известность диагонали также не дает возможности определить длину и ширину, так как существует множество прямоугольников с одинаковыми диагональю и периметром, но с разной площадью.

Как вычислить площадь прямоугольника, если известны длина и ширина?

Для вычисления площади прямоугольника по известным длине и ширине необходимо воспользоваться формулой: S = l*w, где S — площадь, l — длина, w — ширина. Подставляем известные значения и находим значение площади.

Можно ли найти длину прямоугольника по его площади и периметру?

Длину прямоугольника можно вычислить по его площади и периметру только при условии, что известна ширина. Для этого следует воспользоваться формулой: P = 2(l+w), где P — периметр, l — длина, w — ширина. Из формулы выражаем значение ширины: w = (P-2l)/2. Подставляем значение ширины и выражаем длину через площадь: l = S/w.

Как найти площадь неправильного четырехугольника?

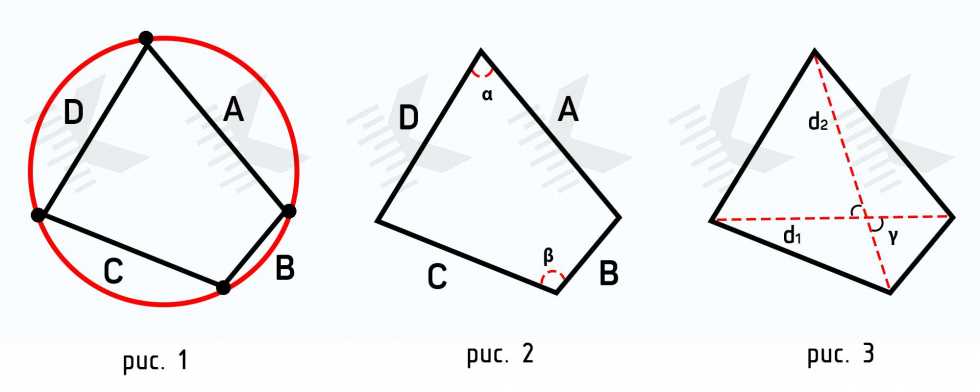
Первый способ расчета основан на формуле Брахмагупты (рис. 1), которая выражает площадь вписанного в окружность четырёхугольника как функцию длин его сторон. Эта формула является обобщением формулы Герона для площади треугольника.

где P — полупериметр, a, b, c, d — длины сторон четырехугольника.

Вторая формула также основывается на формуле Брахмагупты, но на ее расширенной версии (рис. 2), когда необходимо найти площадь произвольного четырехугольника.

где P — полупериметр, a, b, c, d — длины сторон, θ — полусумма противоположных углов четырёхугольника.

В формулах Брахмагупты есть одно ограничение — любая из сторон не может превышать полупериметр. В противном случае стороны четырехугольника не замкнутся. Математически, в формуле появится отрицательное значение. 

Последняя формула позволяет найти площадь не самопересекающейся фигуры по проведенным диагоналям и синусу угла между ними (рис. 3). По сути, формула основывается на сумме площадей треугольников, которые образуются диагоналями четырехугольника.

Заключение

Внимательно изучив все вышеизложенное, можно сделать вывод — определение площади произвольного четырёхугольника с разными сторонами сложнее, чем у них же специальных видов — квадрата, прямоугольника, ромба, трапеции, параллелограмма. Однако внимательно изучив все приведённые методы, можно с лёгкостью решать задачи необходимые для школьников. Сведём все наши формулы в одну таблицу:

1. S = 1/2*d1*d2*sin(d1,d2);
2. S = rad(( p − a )*( p − b )*( p − c )*( p − d ) − a*b*c*d*c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d);
3. S = ((a + b+ c + d)/2)*r

S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине периметра​.

Таким образом, реально сложной является только формула номер 2, но и она вполне доступна, при условии хорошего понимания данных в статье определений и соглашений.