Площадь трапеции (формула) и как ее найти для любой трапеции на рисунке

Периметр трапеции

Периметр фигуры — это числовая характеристика, которая рассчитывается как сумма длин всех сторон n-угольника. Трапеция — это четырехугольник и в общем случае все его стороны имеют разную длину, поэтому периметр рассчитывается по формуле:

P = a + b + c + d,

где a и c – основания фигуры, b и d – ее боковые стороны.

Несмотря на то, что при вычислении периметра трапеции нам нет нужды узнавать высоту, программный код калькулятора требует ввода этой переменной. Так как высота никак не влияет на вычисления, при использовании нашего онлайн-калькулятора вы можете ввести любое значение высоты, которое больше нуля. Рассмотрим пару примеров.

Свойства диагоналей трапеции

Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.

Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции.
Данный отрезок параллелен основаниям трапеции.
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.

LM = (AD — BC)/2

или
LM = (a-b)/2

Свойства треугольников, образованных диагоналями трапеции

Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными.

Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.

Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.

Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.

Свойства трапеции, достроенной до треугольника

Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований.
Таким образом, любая трапеция может быть достроена до треугольника. При этом:

Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника

Свойства отрезка, соединяющего основания трапеции

Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей ( KO/ON ) будет равно соотношению оснований трапеции ( BC/AD ).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).

Свойства отрезка, параллельного основаниям трапеции

Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:

Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
Длина отрезка, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)

Особые виды четырехугольников

Подробнее о каждом из особых видов четырехугольника можно узнать, перейдя по ссылкам выше. Как видно из рисунка, особые виды четырехугольников наследуют свойства своих «предков». Например, прямоугольник (на рисунке показан темно-синим цветом) является особым случаем параллелограмма (на рисунке показан голубым цветом). Таким образом, у него сохраняются все его свойства и добавляются свои, особенные. Поэтому при решении задач про прямоугольники можно применять все свойства и теоремы параллелограмма. Квадрат (на рисунке показан оранжевым цветом) — частный случай прямоугольника. То есть квадрат имеет все свойства параллелограмма, прямоугольника, а также и свои, особенные. Но, самое интересное, квадрат также является частным случаем ромба (на рисунке показан красным цветом), то есть, кроме указанных (параллелограмм, прямоугольник), он обладает еще и всеми свойствами ромба.

Также, интересными особыми случаями четырехугольника являются трапеция и дельтоид.

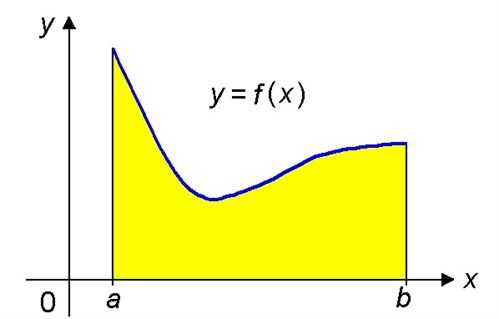
Формула площади криволинейной трапеции

Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.

Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a)
. В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.

Используем формулу Пика

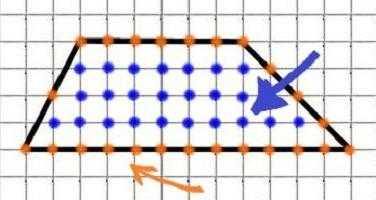
S = M/2 + N — 1,

в этой формуле M — количество узлов, т.е. пересечений линий фигуры с линиями клетки на границах трапеции (оранжевые точки на рисунке), N — количество узлов внутри фигуры (синие точки). Удобнее всего пользоваться ею при нахождении площади неправильного многоугольника. Тем не менее, чем больше арсенал используемых методик, тем меньше ошибок и лучше результаты.

Разумеется, приведенными сведениями далеко не исчерпываются типы и свойства трапеции, а также способы поиска ее площади. В этой статье дан обзор наиболее важных ее характеристик

В решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности

Собранные воедино самые распространенные формулы помогут ученикам сориентироваться в разнообразных способах вычисления площади трапеции и более качественно подготовиться к тестам и контрольным работам по этой теме.

Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз))

Теперь подробно и по порядку.

Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.

Если боковые стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.

В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху. Но никто не запрещает изображать её и наоборот. Вот эскизы:

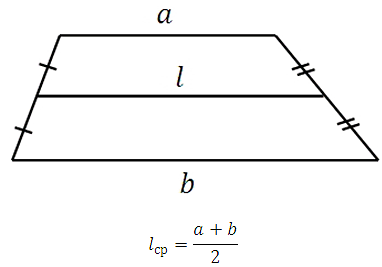
Теперь давайте вникнем глубже. Почему именно так?

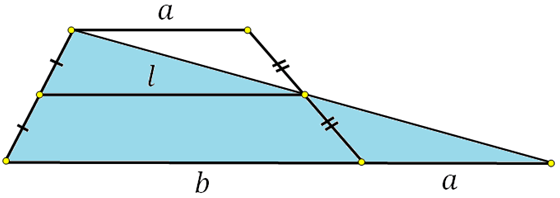
Рассмотрим трапецию с основаниями a и b
и со средней линией l

, и выполним некоторые дополнительные построения: через основания проведём прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:

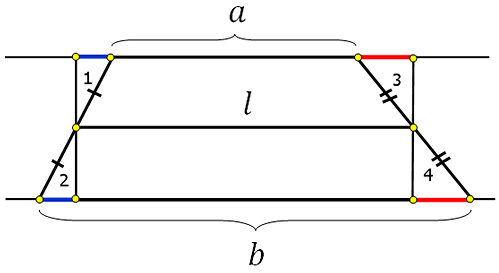
*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.

Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое. Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).

Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии. Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции

Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:

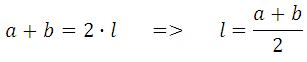
Посмотреть ещё одно объяснение

Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:

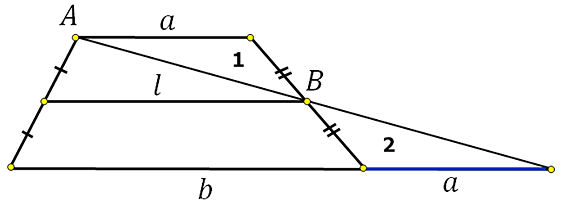
Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников). Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.

Теперь рассмотрим треугольник:

*Средняя линия данной трапеции и средняя линия треугольника совпадают.

Известно, что треугольника равна половине параллельного ей основания, то есть:

Хорошо, разобрались. Теперь о площади трапеции.

Геометрия трапеции

Трапеция (от греч. «трапезион» — стол) — это фигура на плоскости, ограниченная четырьмя отрезками, два из которых параллельны, а два — нет. Параллельные отрезки носят название оснований трапеции, а непараллельные — боковых сторон фигуры. Боковые стороны и их углы наклона определяют вид трапеции, которая может быть разносторонней, равнобедренной или прямоугольной. Помимо оснований и боковых сторон, трапеция имеет еще два элемента:

высота — расстояние между параллельными основаниями фигуры;
средняя линия — отрезок, соединяющий середины боковых сторон.

Данная геометрическая фигура широко распространена в реальной жизни.

Свойства трапеции

Средняя линия трапеции
параллельна основаниям и равна их полусумме
Отрезок, соединяющий середины диагоналей
, равен половине разности оснований и лежит на средней линии. Его длина
Параллельные прямые, пересекающие стороны любого угла трапеции, отсекают от сторон угла пропорциональные отрезки (см. Теорему Фалеса)
Точка пересечения диагоналей трапеции
, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой (см. также свойства четырехугольника)
Треугольники, лежащие на основаниях
трапеции, вершины которых являются точкой пересечения ее диагоналей являются подобными. Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
Треугольники, лежащие на боковых сторонах
трапеции, вершины которых являются точкой пересечения ее диагоналей являются равновеликими (равными по площади)
В трапецию можно вписать окружность
, если сумма длин оснований трапеции равна сумме длин её боковых сторон. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
Отрезок, параллельный основаниям
и проходящий через точку пересечения диагоналей, делится последней пополам и равен удвоенному произведению оснований, деленному на их сумму 2ab / (a +b) (Формула Буракова)

Углы трапеции

бывают острые, прямые и тупые

У прямоугольной трапеции два угла прямые
, а два других – острый и тупой. У других видов трапеций бывают: два острых угла и два тупых.

Тупые углы трапеции принадлежат меньшему
по длине основанию, а острые – большему
основанию.

Любую трапецию можно рассматривать как усеченный треугольник
, у которого линия сечения параллельна основанию треугольника

Важно

Обратите внимание, что таким способом (дополнительным построением трапеции до треугольника) могут решаться некоторые задачи про трапецию и доказываются некоторые теоремы

Что такое трапеция?

Трапеция — это геометрическая фигура, которая имеет две параллельные стороны и две непараллельные стороны. Одна из непараллельных сторон называется большей основой, а другая — меньшей основой. Трапеция также имеет две параллельные боковые стороны, которые соединяют соответствующие концы основ.

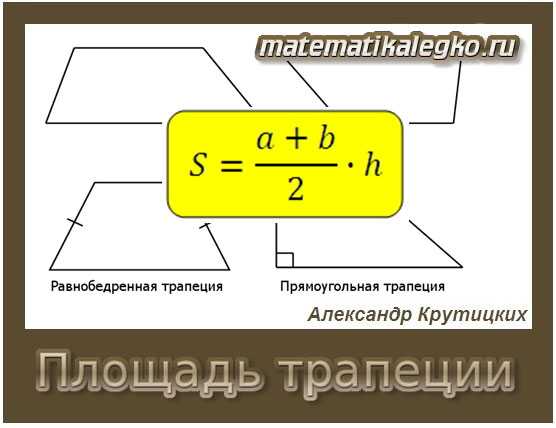
Верно ли утверждение, что площадь трапеции равна произведению средней линии на высоту? Да, это верно. Для нахождения площади трапеции можно использовать формулу: S = ((a + b) / 2) * h, где а и b — основы трапеции, h — высота трапеции. Средняя линия — это средняя арифметическая длина двух основ трапеции.

Поэтому площадь трапеции можно выразить как произведение средней линии на высоту. Применение этой формулы позволяет найти площадь трапеции, не зная длину ни одной из ее сторон, а только среднюю линию и высоту.

Определение трапеции

Трапеция — это четырехугольник, у которого две противоположные стороны параллельны друг другу. Он имеет две основания — большое и малое, и две непараллельные боковые стороны.

Если известно, что площадь трапеции равна произведению средней линии на высоту, то можно найти площадь трапеции, зная эти два параметра. Средняя линия трапеции величиной равна полусумме ее оснований.

Формула для вычисления площади трапеции выглядит следующим образом:

Площадь = (a + b) * h / 2

Где:

а и б — длины оснований трапеции;

h — высота трапеции.

Формула площади трапеции

Площадь трапеции вычисляется по формуле, которая основывается на длине средней линии и высоте. Эта формула утверждает, что площадь трапеции равна произведению средней линии на высоту.

Но верно ли это утверждение? Чтобы убедиться, давайте рассмотрим определение площади трапеции и произведем несколько расчетов.

Трапеция — это четырехугольник, у которого параллельные стороны называются основаниями, а отрезок, соединяющий основания и перпендикулярный им, называется высотой.

Для вычисления площади трапеции необходимо знать длины ее оснований и высоту. Формула, которая выражает эту зависимость, гласит:

Где S — площадь трапеции, a и b — длины оснований, h — высота.

Таким образом, формула подтверждает, что площадь трапеции действительно равна произведению средней линии на высоту.

Формула площади трапеции через среднюю линию и высоту

Формула для нахождения площади трапеции заключается в умножении длины средней линии трапеции на ее высоту, а затем делении полученного произведения на 2.

Средняя линия трапеции представляет собой отрезок, соединяющий середины параллельных сторон. Она имеет половину суммы длин оснований трапеции.

Высота трапеции — это перпендикуляр, опущенный из одного из вершин трапеции на противоположное основание. Она обозначает расстояние между параллельными основаниями трапеции.

Таким образом, если мы умножим длину средней линии на высоту и поделим полученное произведение на 2, то получим площадь трапеции. Формула площади трапеции через среднюю линию и высоту выглядит так: S = (a + b) * h / 2, где a и b — длины оснований трапеции, h — высота трапеции.

Таким образом, мы можем с уверенностью сказать, что формула для вычисления площади трапеции через среднюю линию и высоту верна и позволяет нам эффективно рассчитывать площадь данной геометрической фигуры.

Использование формулы для вычисления площади

Вычисление площади трапеции осуществляется с помощью специальной формулы, которая основана на различных параметрах фигуры. В частности, площадь трапеции можно найти через произведение средней линии на высоту.

Средняя линия трапеции — это среднее арифметическое значение длин двух ее параллельных сторон. Высота же трапеции представляет собой перпендикуляр к параллельным сторонам, проведенный между ними.

Таким образом, применение формулы для вычисления площади позволяет найти площадь трапеции, учитывая значения средней линии и высоты. Однако, верно ли, что площадь трапеции равна именно произведению средней линии на высоту, зависит от конкретной формулы, которая применяется.

В общем случае, формула для вычисления площади трапеции использует длину оснований и высоту фигуры. Она выглядит следующим образом:

S = ((a + b) / 2) * h

Где S — площадь трапеции, a и b — длины оснований, а h — высота фигуры. В этой формуле нет явного указания на произведение средней линии и высоты.

Таким образом, использование формулы для вычисления площади трапеции основывается на соотношении длин оснований и высоты, а не на произведении средней линии и высоты. Эта формула позволяет получить точное значение площади трапеции при заданных параметрах фигуры.

Практический пример расчета площади трапеции

Для понимания и применения формулы для расчета площади трапеции можно рассмотреть пример на практике. Предположим, у нас есть трапеция с основаниями длиной 6 см и 10 см. Кроме того, мы знаем, что высота трапеции равна 4 см.

Для определения площади трапеции воспользуемся формулой, которая гласит: площадь трапеции равна произведению суммы оснований на высоту, деленное на 2.

В нашем случае, сумма оснований равна 6 см + 10 см = 16 см. Подставляем полученные значения в формулу:

Площадь = (6 см + 10 см) * 4 см / 2

Площадь = 16 см * 4 см / 2

Площадь = 64 см² / 2

Площадь = 32 см².

Таким образом, площадь данной трапеции равна 32 см².

Такой результат подтверждает верность утверждения, что площадь трапеции равна произведению суммы оснований на высоту, деленное на 2. В данном примере, средняя линия трапеции равна 8 см (сумма оснований деленная на 2), что подтверждает полученный результат.

Формулы длявычисления площади равнобедренной инеправильной трапеций

Площадь трапеции равна произведению половины суммы оснований на высоту:

\(S = \frac{1}{2} (a+b) \times h.\)

Через длины всех сторон (Формула Герона)

Чтобы посчитать площадь через длины сторон, можно воспользоваться следующей формулой:

\(S = \frac{1}{2} (a+b) \times \sqrt{c^{2} — (\frac{(a — b)^{2} + c^{2} — d^{2}}{2 (a — b)})^{2}}.\)

Существует более простая формула, известная, как формула Герона. Для облегчения ее запоминания вводится р, полусумма всех четырех сторон:

\(p = \frac{1}{2} (a+b+c+d).\)

Формула Герона выглядит так: \(S = \frac{a + b}{\left|a\;-\;b\right|} \times \sqrt{(p — a) (p — b) (p — a — c) (p — a — d)}.\)

Через диагонали и угол между ними

\(S = \frac{1}{2}\times d_{1} \times d_{2} \times \sin\alpha.\)

Здесь \(d_{1}\) и \(d_{2}\) — диагонали, а \(\alpha\) — угол, образованный ими.

Через радиус вписанной окружности

Примечание

Вписать окружность в трапецию можно только тогда, когда сумма ее оснований равна сумме боковых сторон.

Площадь любой трапеции можно найти через радиус вписанной окружности, зная длину оснований:

\(S = (a + b) \times r.\)

Площадь равнобокой трапеции также можно найти через круг, вписанный в нее. Для этого нужно знать радиус этого круга, а также угол \(\alpha\) при основании.

\(S = \frac{4r^{2}}{\sin\alpha}.\)

Через среднюю линию, боковую сторону и угол при основании

Такой способ нахождения площади подходит только для равнобоких трапеций. В этой формуле средняя линия обозначается буквой m, боковая сторона — буквой с, а угол при основании — \(\alpha\). Зная длину средней линии и боковой стороны, достаточно найти синус угла и умножить эти значения друг на друга:

\(S = m \times c \times \sin\alpha.\)

Площадь каких видов трапеций может рассчитать наш калькулятор?

Калькулятор площади трапеции может рассчитать площадь всех видов трапеций, включая прямоугольную, равнобокую, равнобедренную, криволинейную и изогнутую трапеции. Для расчета площади трапеции необходимо знать длины ее оснований и высоту. Если речь идет о криволинейной трапеции или изогнутой трапеции, то также необходимо знать длины наклонных боковых сторон.

Калькулятор площади трапеции учитывает все эти параметры и автоматически рассчитывает площадь трапеции, когда вы вводите соответствующие значения в поля веб-интерфейса калькулятора.

Вопросы и ответы

При расчете площади трапеции могут возникать различные вопросы. Вот некоторые из наиболее частых вопросов и ответы на них:

Как найти высоту трапеции, если она неизвестна?

Высота трапеции является перпендикулярной линией, проведенной от одного основания до другого. Если вы не знаете высоту, но знаете длины оснований и площадь трапеции, то можно использовать формулу S = (a + b)h/2, где S — площадь, a и b — длины оснований, h — высота. Решая эту формулу относительно h, вы получите высоту трапеции: h = 2S / (a + b).

Как рассчитать площадь криволинейной трапеции?

Чтобы рассчитать площадь криволинейной трапеции, необходимо знать длины ее оснований и наклонных боковых сторон, а также высоту. Затем вы можете использовать формулу для площади трапеции: S = (a + b)h/2, где a и b — длины оснований, h — высота. Для криволинейной трапеции вместо a и b необходимо использовать длины соответствующих наклонных сторон.

Как проверить, что я правильно рассчитал площадь трапеции?

Вы можете проверить правильность своих расчетов, используя формулу для площади трапеции. Также вы можете использовать наш онлайн калькулятор площади трапеции, чтобы проверить свои расчеты. Если вы измерили длины сторон и углы трапеции с помощью инструментов, то также можете проверить свои измерения, сравнив их с теоретическими значениями.

Можно ли рассчитать площадь трапеции, зная только диагонали?

Если вы знаете длины диагоналей трапеции и угол между ними, то можно использовать формулу для расчета площади трапеции: S = (1/2)d1d2sin(theta), где d1 и d2 — диагонали, а theta — угол между ними.

Определяем трапецию

Что это за фигура в целом? Трапецией называют многоугольник из четырех углов с двумя параллельными сторонами. Две другие стороны трапеции могут быть наклонены под различными углами. Ее параллельные стороны называют основаниями, а для непараллельных сторон применяют наименование «боковые стороны» или «бедра». Такие фигуры довольно часто встречаются в обыденной жизни. Контуры трапеции можно увидеть в силуэтах одежды, предметах интерьера, мебели, посуды и многих других. Трапеция бывает разных видов: разносторонняя, равнобокая и прямоугольная. Более детально их типы и свойства разберем далее в статье.

Все формулы площади трапеции. найти онлайн