Онлайн-калькулятор расчета площади четырехугольника

Определенный интеграл.Задачи, приводящие к понятию определенного интеграла

Задача 1 (о вычислении площади криволинейной трапеции).

В декартовой прямоугольной системе координат xOy дана фигура (см. рисунок), ограниченная осью х, прямыми х = a, х = b (a \( S_n = f(x_0)\Delta x_0 + \dots + f(x_k)\Delta x_k + \dots + f(x_)\Delta x_ \) Здесь ради единообразия обозначений мы считаем, что a = х, b = x_n; \( \Delta x_0 \) — длина отрезка [x; x₁], \( \Delta x_1 \) — длина отрезка [x₁; x₂], и т.д; при этом, как мы условились выше, \( \Delta x_0 = \dots = \Delta x_ \)

Итак, \( S \approx S_n \), причем это приближенное равенство тем точнее, чем больше n. По определению полагают, что искомая площадь криволинейной трапеции равна пределу последовательности (S_n): $$ S = \lim_ S_n $$

Задача 2 (о перемещении точки) По прямой движется материальная точка. Зависимость скорости от времени выражается формулой v = v(t). Найти перемещение точки за промежуток времени . Решение. Если бы движение было равномерным, то задача решалась бы очень просто: s = vt, т.е. s = v(b-а). Для неравномерного движения приходится использовать те же идеи, на которых было основано решение предыдущей задачи. 1) Разделим промежуток времени на n равных частей. 2) Рассмотрим промежуток времени [t_k; t_k+1] и будем считать, что в этот промежуток времени скорость была постоянной, такой, как в момент времени t_k. Итак, мы считаем, что v = v(t_k). 3) Найдем приближенное значение перемещения точки за промежуток времени [t_k; t_k+1], это приближенное значение обозначим s_k\( s_k = v(t_k) \Delta t_k \) 4) Найдем приближенное значение перемещения s: \( s \approx S_n \) где \( S_n = s_0 + \dots + s_ = v(t_0)\Delta t_0 + \dots + v(t_) \Delta t_ \) 5) Искомое перемещение равно пределу последовательности (S_n): $$ s = \lim_ S_n $$

Подведем итоги. Решения различных задач свелись к одной и той же математической модели. Многие задачи из различных областей науки и техники приводят в процессе решения к такой же модели. Значит, данную математическую модель надо специально изучить.

Что такое прямоугольник

Давайте не будем «срезать углы». Чтобы иметь возможность вычислить площадь прямоугольника, естественно, что мы сначала знаем, что это такое. Поэтому для начала необходимо помнить, что прямоугольник является четырехугольником. Другими словами, это геометрическая фигура, которая имеет четыре стороны и четыре прямых угла. Противоположные стороны прямоугольника имеют одинаковую длину. Две самые длинные стороны представляют его длину, а две другие стороны представляют его ширину.

Не все четырехугольники являются прямоугольниками. Действительно, обязательно, чтобы они имели следующие свойства, чтобы мы могли сказать, что это действительно прямоугольник:

Площадь земельного участка

Онлайн калькулятор расчета. Калькулятор расчета площади земельного участка по длине его четырех сторон. Введите длину сторон участка и рассчитайте его онлайн.

Простой способ рассчитать участка онлайн

прекрасная и простая программа

супер.благодарю.просто и ясно

Калькуляторы

WPcalc — Создавайте любые онлайн калькуляторы

Смотрим на картинку — многоугольника ABCDE можно вычислить как сумму площадей треугольников ABD, BCD и ADE.

Измерение Покупка земельного может быть связана с некоторыми трудностями, как то произведение замеров, оформление документации, регистрация в надзорных органах.

Но измерение может понадобится и в других случаях.

Это обычно происходит, когда нужно: Так или иначе, с такой необходимостью может столкнуться каждый из нас.

Онлайн-калькулятор расчета площади четырехугольника: по сторонам и тд

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

В публикации представлены онлайн-калькуляторы и формулы для расчета площади выпуклого четырехугольника по разным исходным данным: через диагонали и угол между ними, по всем сторонам (если вокруг можно описать окружность), по полупериметру и радиусу вписанной окружности.

• Расчет площади
  • 1. Через диагонали и угол между ними
  • 2. По всем сторонам (формула Брахмагупты)
  • 3. Через полупериметр и радиус вписанной окружности

Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.

2. По всем сторонам (формула Брахмагупты)

Примечание: Если вокруг четырехугольника можно описать окружность.

p – полупериметр четырехугольника, равняется:

S = p ⋅ r

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Все формулы по геометрии. Площади фигур

Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.

Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!

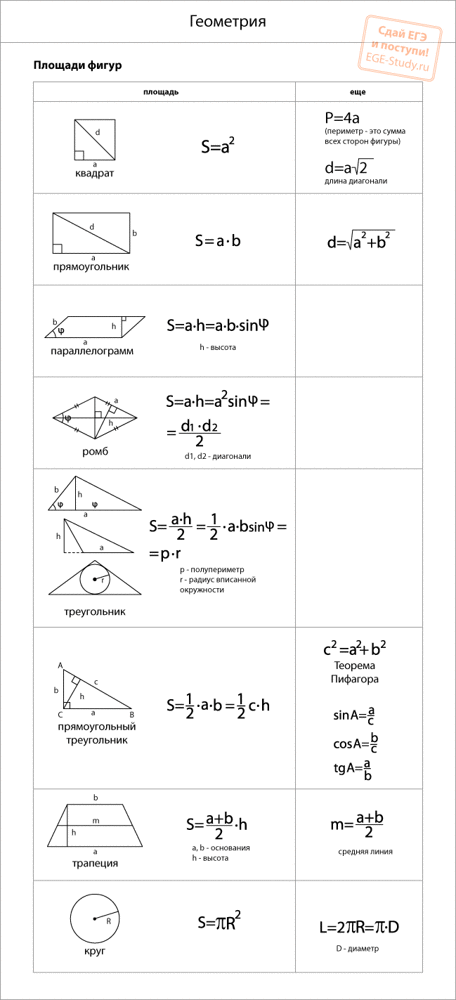
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.

1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: .

2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: .

3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена.

Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности.

Угол, на который опирается эта дуга, также в  раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в  раз меньше, чем площадь всего круга.

Ответ: .

о задачах на тему «Координаты и векторы». Для их решения вспомните, что такое абсцисса точки (это ее координата по ) и что такое ордината (координата по ).

Пригодятся также такие понятия, как координаты вектора и длина вектора (она находится по теореме Пифагора), синус и косинус угла, угловой коэффициент прямой, уравнение прямой, а также сумма, разность и скалярное произведение векторов, угол между векторами.

Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними

Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.

Определения

Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.

Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.

Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться нашим «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°

Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:

В статье собраны несколько калькуляторов, вычисляющих площади неправильных четырехугольников.

Есть несколько способов найти площадь неправильного четырехугольника.

1. Вы знаете длины диагоналей и размер угла между ними. Тогда площадь четырехугольника можно найти по формуле

1. Вы знаете длины четырех сторон и размеры двух противолежащих углов. Тогда площадь четырехугольника можно найти по формуле Бретшнайдера.

, где s — полупериметр.

Площадь четырехугольника по четырем сторонам и двум противолежащим углам

1. Вы знаете длины четырех сторон и длины диагоналей. Тогда площадь четырехугольника тоже можно найти по формуле Бретшнайдера.

, где s — полупериметр

Площадь четырехугольника по четырем сторонам и двум диагоналям

1. Вы знаете длины четырех сторон и то, что четырехугольник является вписанным в окружность. Тогда вы имеете дело с частным случаем формулы Бретшнайдера (сумма двух противолежащих углов известна и равна 180), известным как формула Брахмагупты.

, где s — полупериметр

Для вычисления можно использовать калькулятор выше, введя произвольно два угла так, чтобы их сумма составляла 180.

Вывод самих формул Бретшнайдера можно посмотреть здесь.

Ну и напоследок еще раз упомяну, что зная только длины четырех сторон вычислить площадь четырехугольника нельзя, так как нельзя однозначно определить его вид — нужно еще какое-нибудь ограничивающее условие. Так как у нас на сайте довольно часто просили посчитать площадь четырехугольника только по четырем сторонам, то еще есть вот такой вот шуточный калькулятор: Площадь неправильного четырехугольника с заданными сторонами, который бесконечно рассчитывает такие площади.

Формула площади прямоугольника

Площадь прямоугольника

равна произведению длин двух его смежных сторон

S = a · b

где S – Площадь прямоугольника,

a, b

– длины сторон прямоугольника.

Формулы площадей фигур по геометрии

Начнём из самого интересного множества.

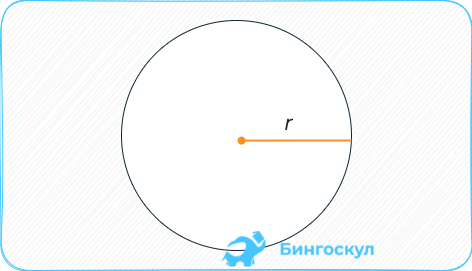
Круг

Равна произведению радиуса в квадрате на π.

S= πr2.

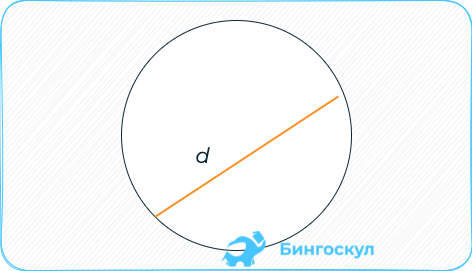
Если известен диаметр – четверти его квадрата на π.

S = pi frac {d^2}{4}, потому что d = frac {1}{2}r, d^2 = frac {1}{4}r^2.

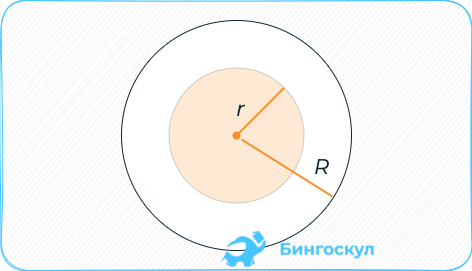
Кольцо круга: разница между площадями кольца и круга.

S =π (R2 – r2).

Четырёхугольники

Рассмотрим, как в геометрии найти все площади фигур, имеющих по четыре угла.

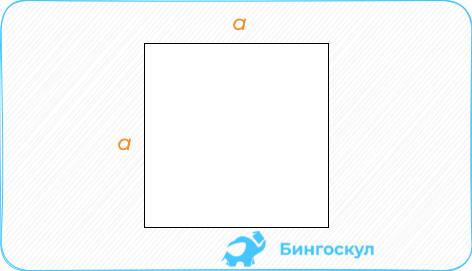
Квадрат: размеры сторон перемножаются.

S = a * a = a2.

Также площадь вычисляется как половина квадрата диагонали.

S = frac {1}{2}d^2 .

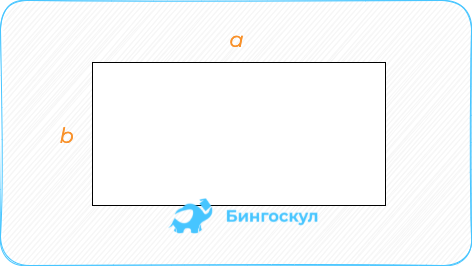
Прямоугольник: произведение соседних сторон – длины на ширину.

S = ab.

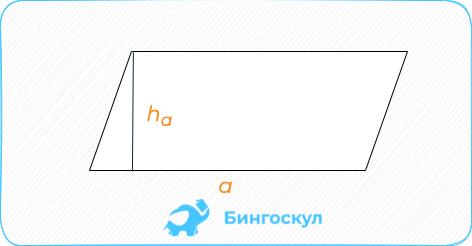
Параллелограмм: умножение длины стороны на опущенную к ней высоту.

S = aha либо S = bhb.

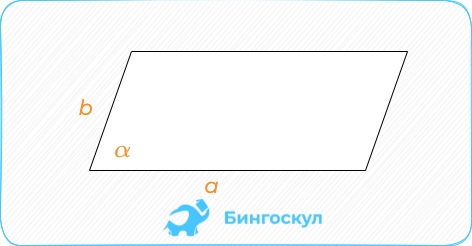
Вторая формула применяется, когда известны длины сторон с углом между ними – произведение сторон на sin угла, под которым они пересекаются.

S = ab*sin α.

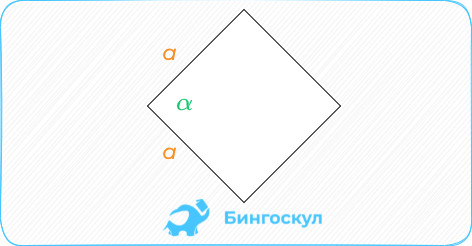
Ромб – параллелограмм с равными сторонами. Если известна сторона, площадь ромба вычисляется как произведение sin угла между сторонами на их длину в квадрате.

S = a2*sin α.

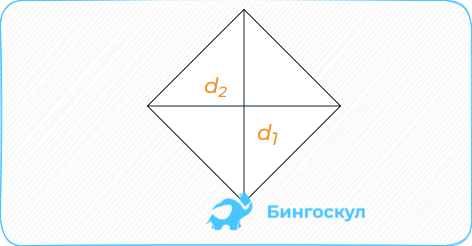
Если в задании даны длины диагоналей, площадь определяется как половина их произведения.

S = frac {1}{2}d^1d^2 .

При наличии одной диагонали (полудиагонали) и стороны, неизвестные данные вычисляются по теореме Пифагора.

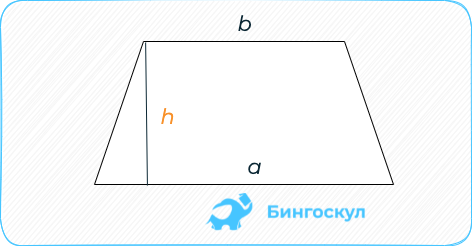
Трапеция: полусумма длин верхнего и нижнего оснований на высоту геометрической фигуры.

S = frac {a+b}{2}h .

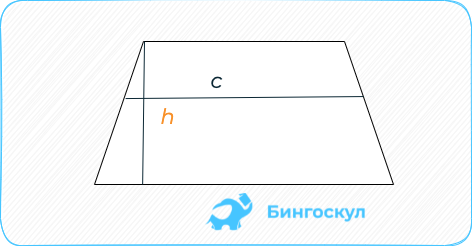
Когда даны средняя линия и высота, площадь находят путём перемножения их значений.

S = ch.

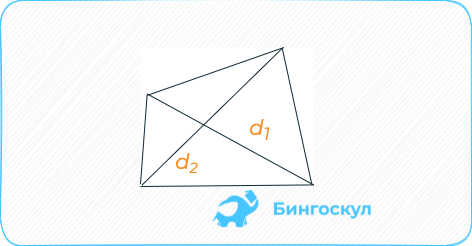
Выпуклый четырёхугольник: половина длины диагоналей, перемноженная на sin угла, который они образуют.

S = d1d2 * sinα.

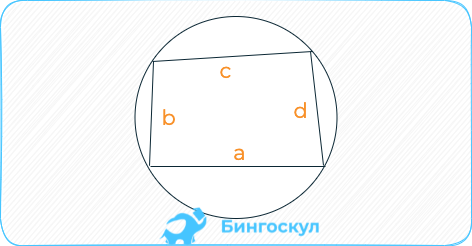
Вписанный в окружность 4-угольник: площадь вычисляется как корень квадратный из произведения разности периметра на длину каждой стороны.

S = sqrt { (p-a)*(p-b)*(p-c)*(p-d) } .

В случае с прямоугольником, квадратом формула упрощается.

Треугольники

Способов расчёта занимаемого треугольником места на плоскости множество. Это произведение:

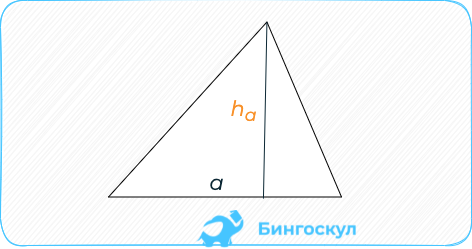
Половины стороны на проведённую к ней высоту.

S = ½ aha.

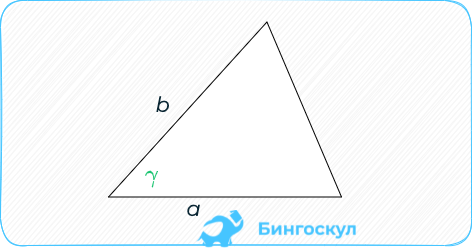
Пары любых сторон на sin образуемого ими угла:

S = ab * sin γ.

Квадрата полупериметра геометрической фигуры на тангенсы половин углов.

S = p2 * tgα/2 * tgβ/2 * tgγ/2.

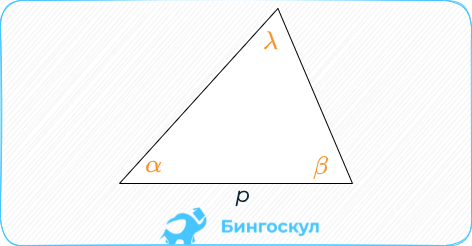
Корню квадратному произведения разницы полупериметров и сторон.

S = sqrt { (p-a)*(p-b)*(p-c) } .

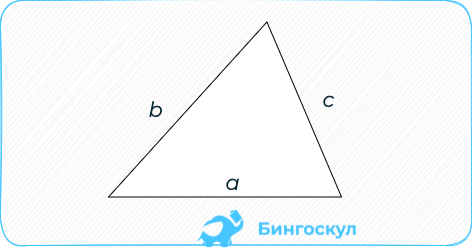
Квадрата длины стороны на синусы смежных углов, разделённому на удвоенный синус третьего, противоположного ей угла.

S = frac { a^2 sin beta `* sin sin gamma } { 2 sin sin alpha}  .

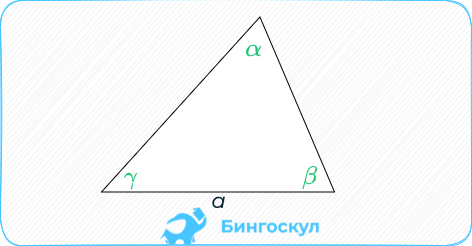
При известной высоте: отношению её произведения на синус угла, откуда та опущена, к двойному произведению синусов остальных углов.

S = frac { h^2 sin sin alpha } { 2 sin beta *sin sin gamma }  .

Для прямоугольного 3-угольника, по сути, половины прямоугольника, применимо выражение:

S = frac { ab }{ 2 }.

Многоугольники

Для фигур с пятью и большим числом сторон применяют правило: площадь вычисляется путём умножения количества углов на квадрат длины стороны и тангенс отношения числа Пи к количеству сторон.

S = frac { n }{ 4 } a^2 ctg ( frac { pi }{ n }) .

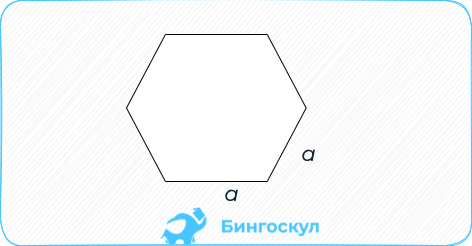
1. Формула Герона для трапеции

   S =	a + b	√(p-a)(p-b)(p-a-c)(p-a-d)
   |a – b|

2. Формула площади трапеции по длине основ и высотеПлощадь трапеции

   равна произведению полусуммы ее оснований на высоту

   где S – площадь трапеции,a, b – длины основ трапеции,c, d – длины боковых сторон трапеции,

   p =	a + b + c + d	– полупериметр трапеции.
   2

Как найти площадь неправильного четырехугольника?

Один из наиболее простых способов — разделить неправильный четырехугольник на два или более треугольников. Зная длины сторон треугольников и используя формулу Герона или другие методы нахождения площади треугольника, можно найти площадь каждого из них и затем сложить полученные значения.

Если известны длины четырех сторон неправильного четырехугольника и углы между ними, можно использовать формулу для нахождения площади по длинам сторон и углам. Для этого нужно разделить четырехугольник на два треугольника и применить формулу для нахождения площади треугольника с учетом величины угла между сторонами.

В случае, если известны координаты вершин неправильного четырехугольника, можно воспользоваться формулой площади Гаусса. Для этого нужно последовательно соединить вершины всех четырехугольников прямыми линиями и посчитать алгебраическую сумму площадей полученных треугольников.

Площадь четырехугольника по сторонам

Когда известны длины сторон фигуры, можно применить формулу площади четырехугольника по сторонам. Для применения этих расчетов потребуется найти полупериметр фигуры. Мы помним, что периметр – это сумма длин всех сторон. Полупериметр – это половина периметра. В нашем прямоугольнике со сторонами a, b, c, d
формула полупериметра будет выглядеть так:
Зная стороны, выводим формулу. Площадь четырехугольника представляет собой корень из произведения разности полупериметра с длиной каждой стороны:

Рассмотрим пример расчета площади четырехугольника через стороны. Дан произвольный четырехугольник со сторонами a
= 5 см, b
= 4 см, с
= 3 см, d
= 6 см. Для начала найдем полупериметр:
используем найденное значение для расчета площади:

Правило

Площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне.

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Площадь треугольника равна корню квадратному из произведения полупериметра этого треугольника и разностей полупериметра и всех его сторон.

Площадь треугольника равна отношению произведения квадрата его стороны на синусы прилежащих углов к удвоенному синусу противолежащего угла.

Площадь треугольника равна отношению произведения квадрата его высоты на синус угла, из вершины которого проведена эта высота, к удвоенному произведению синусов двух других углов.

Площадь прямоугольного треугольника равна половине произведения его катетов.

Площадь равнобедренного треугольника равна половине произведения его основания на корень квадратный из разности квадратов боковой стороны и половины основания.

Площадь равностороннего треугольника равна четверти произведения квадрата стороны этого треугольника и квадратного корня из трёх.

Площадь равностороннего треугольника равна отношению квадрата его высоты к квадратному корню из трёх.

Площадь треугольника равна отношению произведения всех его сторон к четырём радиусам, описанной около него окружности.

Площадь треугольника равна удвоенному произведению квадрата радиуса, описанной около него окружности, и синусов всех его углов.

Площадь треугольника (многоугольника) равна произведению его полупериметра и радиуса окружности, вписанной в этот треугольник (многоугольник).

Площадь треугольника равна произведению квадрата радиуса вписанной окружности на котангенсы половин всех углов треугольника.

Площадь прямоугольника равна произведению двух соседних его сторон.

Площадь квадрата равна квадрату его стороны.

Площадь квадрата равна половине квадрата его диагонали.

Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне.

Площадь параллелограмма равна произведению двух соседних его сторон на синус угла между ними.

Площадь ромба равна произведению квадрата его стороны на синус одного из его углов.

Площадь ромба (как и дельтоида) равна половине произведения его диагоналей.

Площадь трапеции равна произведению полусуммы её оснований на высоту.

Площадь трапеции равна произведению её средней линии на высоту.

Площадь выпуклого четырёхугольника равна половине произведения его диагоналей на синус угла между ними.

Площадь четырёхугольника, вписанного в окружность, равна корню квадратному из произведения разностей полупериметра этого четырёхугольника и всех его сторон.

Площадь круга равна произведению числа “пи” на квадрат радиуса.

Площадь круга равна четверти произведения числа “пи” на квадрат диаметра.

формулы для случаев градусной и радианной мер центральных углов

Площадь кругового сектора равна произведению площади единичного сектора (сектор, соответствующий центральному углу с мерой равной единице) на меру центрального угла, соответствующего данному сектору.

Площадь кругового кольца равна произведению числа “пи” на разность квадратов внешнего и внутреннего радиусов.

Площадь кругового кольца равна четверти произведения числа “пи” на разность квадратов внешнего и внутреннего диаметров.

Площадь кругового кольца равна удвоенному произведению числа “пи”, среднего радиуса кольца и его ширины.

Давно собирался и вот, наконец! Примерно так выглядит история нашей группы ВКонтакте . Сомнения в необходимости её существования отброшены, и первые материалы сообщества уже выложены.

Расширены функциональные возможности главного меню.

30.12.2015 Галерея на сайте math4school.ru Приглашаю посетить Галерею, – новый раздел на сайте.

27 декабря 2015 года исполнилось 444 года со дня рождения Иоганна Кеплера.

Как посчитать правильно квадратуру стен

Знать площадь стен нужно при покупке строительных материалов — обоев, краски, декоративной штукатурки и т.д. Для этого нужны дополнительные замеры. К существующим уже ширине и длине помещения необходимы будут:

• знать высоту потолка;
• замерить высоту и ширину дверных и оконных проемов.

Все замеры делаются — в квадратных метрах. Вам будет удобно, если все ваши замеры вы нанесете на план. Из-за того, что стены прямоугольные, площадь считаем как для прямоугольника: длину умножаем на ширину. Также считаем размеры оконных и дверных проемов, их величины отнимаем от общей площади помещения.

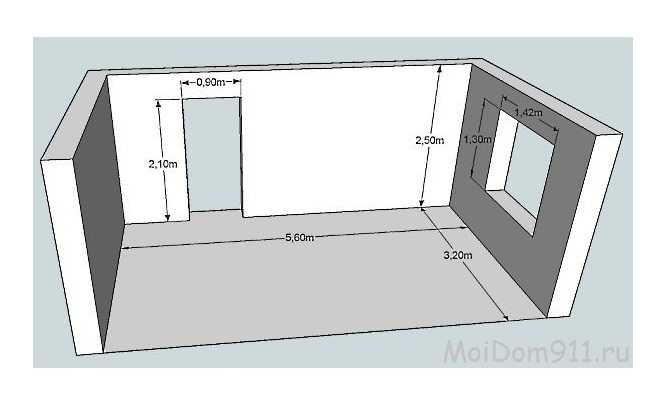
Стена с дверью:

• 2,5 метра * 5,6 метра = 14 м² — получилась общая площадь стены
• дверной проем: 2,1 метра * 0,9 метра = 1,89 м²
• площадь стены без дверного проема: 14 — 1,89 = 12,11 м²

Стена с окном:

• площадь маленьких стен: 2,5 метра * 3,2 метра = 8 м²
• считаем площадь окна: 1,3 метра * 1,42 метра = 1,846 м², округляя, получается 1,85 м²
• стена без окна: 8 кв. м — 1,85 м² = 6,15 м²

Найти общую площадь стен без проемов получается очень просто. Складываем все четыре цифры: 14 м² + 12,11 м². + 8 м² + 6,15 м². = 40,26 м²

Формулы площадей всех основных фигур

Зная диаметр или радиус круга, можно найти его площадь.

r – радиус круга

D – диаметр

Формула площади круга, (S):

h – высота треугольника

a – основание

Площадь треугольника (S):

3. Площадь треугольника, формула Герона

a , b , c , – стороны треугольника

p– полупериметр, p=( a + b + c )/2

Формула ( Герона ) площади треугольника через полупериметр ( S ):

4. Площадь прямоугольного треугольника по катетам

Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.

a , b – катеты треугольника

Формула площади прямоугольного треугольника, (S):

5. Как вычислить площадь равнобедренного треугольника ?

b – основание треугольника

a – равные стороны

h – высота

Формула площади треугольника через высоту h и основание b , ( S ):

Формула площади треугольника через, стороны a , b , (S):

6. Площадь равностороннего треугольника равна:

Формулы расчета, площади равностороннего треугольника.

a – сторона треугольника

h – высота

Площадь треугольника только через сторону a , (S):

Площадь треугольника только через высоту h , ( S ):

Площадь треугольника через сторону a и высоту h , (S):

7. Найти площадь треугольника, угол и две стороны

Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.

a , b , c – стороны треугольника

α , β , γ – углы

Формулы площади треугольника, через две стороны и угол между ними, ( S ):

a , b , c – стороны треугольника

α , β , γ – противолежащие углы

Площадь треугольника через сторону и два угла (S):

b – длина прямоугольника

a – ширина

Формула площади прямоугольника, (S):

10. Как рассчитать площадь квадрата через диагональ или сторону

a – сторона квадрата

c – диагональ

Формула площади квадрата через сторону a , (S):

Формула площади квадрата через диагональ c , (S):

11. Формулы площади параллелограмма

1. Формула площади параллелограмма через стороны и углы

a, b – стороны параллелограмма

α , β – углы параллелограмма

Формула площади через стороны и углы параллелограмма, ( S ):

2. Формула площади параллелограмма через сторону и высоту

a, b – стороны параллелограмма

H _b – высота на сторону b

H _a – высота на сторону a

Формула площади через стороны и высоты параллелограмма, (S):

3. Формула площади параллелограмма через диагонали и угол между ними

D – большая диагональ

d – меньшая диагональ

α , β – углы между диагоналями

Формула площади через диагонали параллелограмма и угол между ними , (S):

12. Площадь произвольной трапеции

1. Формула площади трапеции через основания и высоту

b – верхнее основание

a – нижнее основание

m – средняя линия

h – высота трапеции

Формула площади трапеции, (S):

2. Формула площади трапеции через диагонали и угол между ними

d ₁, d ₂ – диагонали трапеции

α , β – углы между диагоналями

Формула площади трапеции, (S):

3. Формула площади трапеции через четыре стороны

b – верхнее основание

a – нижнее основание

c, d – боковые стороны

Формула площади трапеции, (S):

13. Площадь равнобедренной трапеции

1. Формула площади равнобедренной трапеции через стороны и угол

b – верхнее основание

a – нижнее основание

c – равные боковые стороны

α – угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, (S):

Формула площади равнобедренной трапеции через стороны и угол, (S):

2. Формула площади равнобокой трапеции через радиус вписанной окружности

R – радиус вписанной окружности

D – диаметр вписанной окружности

O – центр вписанной окружности

H – высота трапеции

α , β – углы трапеции

Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d – диагональ трапеции

α , β – углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m – средняя линия трапеции

c – боковая сторона

α , β – углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

b – верхнее основание

a – нижнее основание

h – высота трапеции

Формула площади равнобедренной трапеции через основания и высоту, (S):

Как найти площадь равнобедренного треугольника

1. Умножьте основание на высоту треугольника.
2. Поделите результат на два.

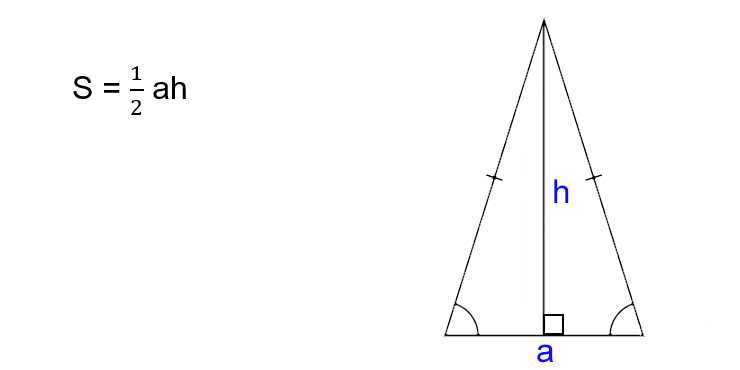
• S — искомая площадь треугольника.
• a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
• h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.

1. Умножьте квадрат стороны треугольника на корень из трёх.
2. Поделите результат на четыре.

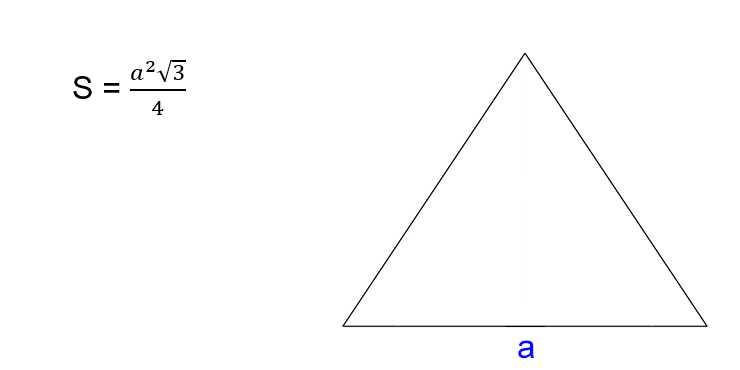
• S — искомая площадь треугольника.
• a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.

❓Вопросы и ответы

Несколько вопросов и ответы на них по калькулятору площади прямоугольника:

Для чего нужен калькулятор площади прямоугольника?

Калькулятор площади прямоугольника может использоваться во многих ситуациях, например, при строительных работах, в дизайне интерьера, при решении задач по геометрии и в повседневной жизни.

Что такое прямоугольник?

Прямоугольник — это геометрическая фигура, которая имеет четыре угла, все из которых прямые (равны 90 градусам), и противоположные стороны параллельны друг другу и имеют равные длины.

По определению, прямоугольник является частным случаем параллелограмма, у которого все углы прямые.

Вычисление площади пола

Если комната стандартная (квадратная или прямоугольная), то вычислить площадь такого помещения сможет каждый. Для этого нужно узнать ширину и длину помещения, после чего просто перемножить эти показатели.

Таким образом, формула будет выглядеть так: S = a * b, где, а и b — длина и ширина помещения.

Если вы рассчитываете площадь помещения для потолка, то встроенные шкафы или камины никак не повлияют на замеры площади.

В случае, если вы собираетесь установить камин или же установить встроенный шкаф-купе, то площадь, которую он будет занимать, нужно обязательно вычислить исходя из предполагаемых размеров конструкции и общих размеров помещения.

Проводить точные замеры помещений, в которых имеется встроенная мебель, необходимо, если вы планируете укладывать напольное покрытие. В случае, если камин или комод занимает не много места, его площадью можно пренебречь, если много — конструкцию на время можно разобрать или высчитать сколько места она занимает.